Understanding Power Anomalies in Mediation Analysis

Abstract

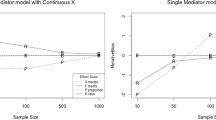
Previous studies have found some puzzling power anomalies related to testing the indirect effect of a mediator. The power for the indirect effect stagnates and even declines as the size of the indirect effect increases. Furthermore, the power for the indirect effect can be much higher than the power for the total effect in a model where there is no direct effect and therefore the indirect effect is of the same magnitude as the total effect. In the presence of direct effect, the power for the indirect effect is often much higher than the power for the direct effect even when these two effects are of the same magnitude. In this study, the limiting distributions of related statistics and their non-centralities are derived. Computer simulations are conducted to demonstrate their validity. These theoretical results are used to explain the observed anomalies.

Appendices

Appendix A

Proof of Proposition 1

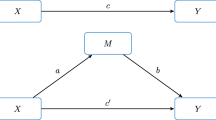
Since $S_{XU} = \sum _i(X_i-\bar{X})U_i$, $S_{XU}$ follows a normal distribution with mean 0 and variance $\sigma ^2_US_{XX}$. According to Eq. (3), ${\hat{a}}$ is unbiased since $E({\hat{a}})=a$. The variance of ${\hat{a}}$ is equal to $n^{-1}\cdot \sigma ^2_U/(n^{-1}S_{XX})$ and converges to 0 as $n\rightarrow \infty$. That is, ${\hat{a}}$ is a consistent estimator of a.

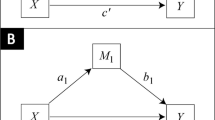
Similar argument shows that ${\hat{c}}$ is unbiased for $ab+c'$. From (4), the variance of ${\hat{c}}$ is equal to $n^{-1}(b^2\sigma ^2_U+\sigma ^2_{V'})/(n^{-1}S_{XX})$ and converges to 0 as $n\rightarrow \infty$. That is, ${\hat{c}}$ is a consistent estimator of $ab+c'$.

To show the unbiasedness of ${\hat{b}}$ and ${\hat{c}}'$, it suffices to show that the expectation of the second term in (5) is $(0, 0)^t$. This is true because

$$\begin{aligned} E\left[ \frac{1}{S_{UU}S_{XX}-S^2_{XU}}\left( \begin{array}{c} A \\ -aA+B \end{array}\right) \right]&= E\left\{ \left. E\left[ \frac{1}{S_{UU}S_{XX}-S^2_{XU}}\left( \begin{array}{c} A \\ -aA+B \end{array}\right) \right] \right| U\right\} \\&= E\left[ \frac{1}{S_{UU}S_{XX}-S^2_{XU}}\left( \begin{array}{c} 0 \\ 0 \end{array}\right) \right] \\&= \left( \begin{array}{c} 0 \\ 0 \end{array}\right) . \end{aligned}$$

Now we prove the consistency of ${\hat{b}}$. The fact that $S_{XU}$ follows a normal distribution with mean 0 and variance $\sigma ^2_US_{XX}$ implies $n^{-1}S_{XU} = O_p(n^{-1/2})$. Similarly, $n^{-1}S_{XV'} = O_p(n^{-1/2})$. The second term of expression (5) can be rewritten

$$\begin{aligned} \frac{1}{n^{-1}S_{UU}\cdot n^{-1} S_{XX}-(n^{-1}S_{XU})^2}\left( \begin{array}{c} n^{-2}A \\ -a\cdot n^{-2}A+n^{-2}B \end{array}\right) . \end{aligned}$$

Because

$$\begin{aligned} n^{-1}S_{UU}\cdot n^{-1}S_{XX} - (n^{-1}S_{XU})^2 = n^{-1}S_{UU}\cdot s^2_X + O_p(n^{-1}), \end{aligned}$$

it suffices to show that $n^{-2}A$ and $n^{-2}B$ converge to 0 in probability. Since the product $U_iV_i'$ are independently and identically distributed, $n^{-1/2}\sum _{i=1}^n U_iV'_i= O_p(1)$. Hence,

$$\begin{aligned} S_{UV'}&= \sum _{i=1}^n U_iV'_i-n^{1/2}\bar{U}\cdot n^{1/2}\bar{V}' \\&= n^{1/2} \cdot n^{-1/2}\sum _{i=1}^n U_iV'_i + O_p(1) \\&= O_p(n^{1/2})+O_p(1)\\&= O_p(n^{1/2}). \end{aligned}$$

We have

$$\begin{aligned} n^{-2} A&= n^{-1}S_{XX}\cdot n^{-1}S_{UV'} - n^{-1}S_{XV'} \cdot n^{-1}S_{XU} \\&= n^{-1}S_{XX}\cdot O_p(n^{-1/2}) + O_p(n^{-1}) \\&= O_p(n^{-1/2}). \end{aligned}$$

This shows ${\hat{b}}$ is consistent for b. In addition,

$$\begin{aligned} n^{-2} B&= n^{-1}S_{UU}\cdot n^{-1}S_{XV'} - n^{-1}S_{UV'} \cdot n^{-1}S_{XU} \\&= O_p(n^{-1/2}) + O_p(n^{-1}) \\&= O_p(n^{-1/2}). \end{aligned}$$

So ${\hat{c}}'$ is consistent for $c'$.

Appendix B

Proof of Proposition 2

The normality of ${\hat{a}}$ and ${\hat{c}}$ is obvious. Their variances and the covariance between them are

$$\begin{aligned} Var[{\sqrt{n}}({\hat{a}}-a)]&= \frac{n\sigma ^2_U}{S_{XX}} \\&= \frac{\sigma ^2_U}{s^2_X}, \\ Var[{\sqrt{n}}({\hat{c}}-c)]&= \frac{nb^2S_{XX}\sigma ^2_U+nS_{XX}\sigma ^2_{V'}}{S_{XX}^2} \\&= \frac{b^2\sigma ^2_U+\sigma ^2_{V'}}{s^2_X}, \end{aligned}$$

and

$$\begin{aligned} Cov[{\sqrt{n}}({\hat{a}}-a), {\sqrt{n}}({\hat{c}}-c)]&= \frac{nbS_{XX}\sigma ^2_U}{S^2_{XX}} \\&= \frac{b\sigma ^2_U}{s_X^2}. \end{aligned}$$

This completes the proof of part 1.

In the proof of Proposition 1, we have seen that

$$\begin{aligned} n^{-1}S_{UU}\cdot n^{-1}S_{XX} - (n^{-1}S_{XU})^2 = n^{-1}S_{UU}\cdot s^2_X+O_p(n^{-1}). \end{aligned}$$

(6)

From expression (5), there is

$$\begin{aligned} {\sqrt{n}}\left( \begin{array}{c} {\hat{b}}-b \\ {\hat{c}}'-c' \end{array}\right)&= \frac{1}{n^{-1}S_{UU}\cdot s^2_X}\left( \begin{array}{c} n^{-3/2}A \\ -a\cdot n^{-3/2}A+n^{-3/2}B \end{array}\right) +O_p(n^{-1}) \end{aligned}$$

Furthermore,

$$\begin{aligned} n^{-3/2}A&= s^2_X\cdot n^{-1/2}S_{UV'} + O_p(n^{-1/2}), \end{aligned}$$

(7)

$$\begin{aligned} n^{-3/2}B&= \sigma ^2_U\cdot n^{-1/2}S_{XV'} + O_p(n^{-1/2}). \end{aligned}$$

(8)

Since $n^{-1/2}S_{UV'}$ converges to $N(0, \sigma ^2_U\sigma ^2_{V'})$ in distribution and $n^{-1/2}S_{XV'}$ follows $N(0, s^2_X\sigma ^2_{V'})$, we have

$$\begin{aligned} \hbox {Var}(n^{-3/2}A)&= (s^2_X)^2\sigma ^2_U\sigma ^2_{V'} + O_p(n^{-1/2}), \\ \hbox {Var}(n^{-3/2}B)&= (\sigma ^2_U)^2s^2_X\sigma ^2_{V'} + O_p(n^{-1/2}), \\ \hbox {Cov}(n^{-3/2}A, n^{-3/2}B)&= O_p(n^{-1/2}), \end{aligned}$$

and

$$\begin{aligned} \hbox {Var}(a\cdot n^{-3/2}A + n^{-3/2}B)&= a^2\hbox {Var}(n^{-3/2}A)+\hbox {Var}(n^{-3/2}B)+O_p(n^{-1/2}). \end{aligned}$$

Combining these results and expression (6) gives the result of part 2 by repeatedly using Slutsky’s theorem.

To prove part 3, we first note that

$$\begin{aligned} \hbox {Cov}\left[ {\sqrt{n}}({\hat{a}}-a), {\sqrt{n}}\left( \begin{array}{c}{\hat{b}}-b\\ {\hat{c}}'-c'\end{array}\right) \right] = \hbox {Cov}\left[ \frac{{\sqrt{n}}S_{XU}}{S_{XX}}, \frac{{\sqrt{n}}}{S_{UU}S_{XX}-S_{XU}^2}\left( \begin{array}{c} A \\ -aA+B\end{array}\right) \right] . \end{aligned}$$

(9)

Because of (7) and (8),

$$\begin{aligned} \hbox {Cov}(n^{-1/2}S_{XU}, n^{-3/2}A)&= n^{-1}s^2_X \hbox {Cov}(S_{XU}, S_{UV'}) +O_p(n^{-1/2}) \nonumber \\&= n^{-1}s^2_X E(S_{XU}S_{UV'}) +O_p(n^{-1/2})\nonumber \\&= n^{-1}s^2_X E[E(S_{XU}S_{UV'}|U)] +O_p(n^{-1/2})\nonumber \\&= n^{-1}s^2_X E(0|U)+O_p(n^{-1/2}) \nonumber \\&= 0+O_p(n^{-1/2}) \nonumber \\&= O_p(n^{-1/2}) \end{aligned}$$

(10)

and

$$\begin{aligned} \hbox {Cov}(n^{-1/2}S_{XU}, n^{-3/2}B)&= n^{-1}\sigma ^2_U \hbox {Cov}(S_{XU}, S_{XV'})+O_p(n^{-1/2}) \nonumber \\&= n^{-1}\sigma ^2_U E(S_{XU}S_{XV'}) +O_p(n^{-1/2})\nonumber \\&= n^{-1}\sigma ^2_U E(S_{XU})\cdot E(S_{XV'}) +O_p(n^{-1/2})\nonumber \\&= 0 +O_p(n^{-1/2})\nonumber \\&= O_p(n^{-1/2}). \end{aligned}$$

(11)

Using expression (9) and Slutsky’s theorem, both Cov$[{\sqrt{n}}({\hat{a}}-a), {\sqrt{n}}({\hat{b}}-b)]$ and Cov$[{\sqrt{n}}({\hat{a}}-a), {\sqrt{n}}({\hat{c}}'-c')]$ converge to 0 in probability.

Similarly, because of (10) and (11),

$$\begin{aligned} \hbox {Cov}(n^{-1/2}S_{XV'}, n^{-3/2}A)&= n^{-1}s^2_X Cov(S_{XV'}, S_{UV'}) +O_p(n^{-1/2}) \\&= n^{-1}s^2_X E(S_{XV'}S_{UV'}) +O_p(n^{-1/2})\\&= n^{-1}s^2_X E[E(S_{XU}S_{UV'}|V')] +O_p(n^{-1/2})\\&= n^{-1}s^2_X E[0|U)]+O_p(n^{-1/2}) \\&= 0+O_p(n^{-1/2}) \\&= O_p(n^{-1/2}), \end{aligned}$$

and

$$\begin{aligned} \hbox {Cov}(n^{-1/2}S_{XV'}, n^{-3/2}B)&= n^{-1}\sigma ^2_U Var(S_{XV'})+O_p(n^{-1/2}) \\&= n^{-1}\sigma ^2_U E\left[ \left( \sum _i(X_i-\bar{X})V_i'\right) ^2\right] +O_p(n^{-1/2})\\&= n^{-1}\sigma ^2_U E\left[ \sum _i(X_i-\bar{X})^2(V_i')^2\right] +O_p(n^{-1/2})\\&= n^{-1}\sum _i(X_i-\bar{X})^2\cdot \sigma ^2_U E\left[ (V_i')^2\right] +O_p(n^{-1/2})\\&= s^2_X \sigma ^2_U \sigma ^2_{V'} +O_p(n^{-1/2}), \end{aligned}$$

The results for Cov$[{\sqrt{n}}({\hat{c}} -(ab+c')), {\sqrt{n}}({\hat{b}}-b)]$ and Cov$[{\sqrt{n}}({\hat{c}} -(ab+c')), {\sqrt{n}}({\hat{c}}'-c')]$ can be proved in a similar manner.