On the universality of the quantum approximate optimization algorithm

Abstract

The quantum approximate optimization algorithm (QAOA) is considered to be one of the most promising approaches towards using near-term quantum computers for practical application. In its original form, the algorithm applies two different Hamiltonians, called the mixer and the cost Hamiltonian, in alternation with the goal being to approach the ground state of the cost Hamiltonian. Recently, it has been suggested that one might use such a set-up as a parametric quantum circuit with possibly some other goal than reaching ground states. From this perspective, a recent work (Lloyd, ar**v:1812.11075) argued that for one-dimensional local cost Hamiltonians, composed of nearest neighbour ZZ terms, this set-up is quantum computationally universal and provides a universal gate set, i.e. all unitaries can be reached up to arbitrary precision. In the present paper, we complement this work by giving a complete proof and the precise conditions under which such a one-dimensional QAOA might produce a universal gate set. We further generalize this type of gate-set universality for certain cost Hamiltonians with ZZ and ZZZ terms arranged according to the adjacency structure of certain graphs and hypergraphs.

1 Introduction

A question in the field of quantum information processing is whether contemporary quantum processors will in the near future be able to solve problems more efficiently than classical computers. Combinatorial optimization problems are of special interest, for which a class of algorithms under the name of quantum approximate optimization algorithm (QAOA) have been proposed [1]. QAOA consists of a bang-bang protocol [2] that is expected to solve hard problems approximately. This procedure involves the unitary evolution under a Hamiltonian encoding the objective function of the combinatorial optimization problem and a second non-commuting mixer Hamiltonian. Since its proposal, QAOA has been extensively studied to understand its performance [3,4,5], for establishing quantum supremacy results [6] and for solving several optimization problems [7,8,9]. This algorithm together with others such as the variational quantum eigensolver (VQE) [10,11,12] is part of the so-called variational hybrid quantum/classical algorithms, combining the computational power of a quantum computer to prepare quantum states with a classical optimizer. These variational algorithms (including QAOA) have shown several advantages such as robustness to noise, yet more study is required to know the limitations in algorithms such as QAOA. Recent work has found limitations in parameterized quantum circuits trained with classical optimizers wherein for large enough problem sizes the algorithms suffer from so-called barren plateaus from which exponentially low probability to escape does not allow the algorithms to achieve an optimal result [13]. The expressive power of parameterized quantum circuits, namely the set of probability distributions, from which a parameterized circuit is able to sample from, has also been studied [14]. In this paper, we study the capacity of QAOA to perform universal quantum computation in the sense that sequences of QAOA unitaries can approximate arbitrary unitaries (as we will detail below); in this setting, one could more aptly call the method the quantum alternating operator ansatz as suggested in Ref. [3].

A proof sketch of the quantum computational universality of a class of QAOA quantum circuits has been given in Ref. [15], implying that QAOA circuits can efficiently simulate arbitrary quantum circuits with polynomial overhead, i.e. it can solve problems in the BQP [16] in polynomial time. In our work, we study a complementary notion of universality, called gate-set universality, which involves the capacity of approximating any unitary (although we will not study the efficiency of our method which we leave as future work). Note that these two notions are not unrelated, but do not imply each other directly. For example, one could construct models of computation for n qubits with a universal gate set that densely generates the unitary group, but the individual gates become exponentially close to the identity as n grows. In this case, the number of gates needed to implement a given non-trivial unitary necessarily would grow exponentially with n, and hence, it would not be quantum computationally universal. However, due to the Solovay–Kitaev theorem [17], it is known that if a gate set can reach a starting $\epsilon$-net in a polynomial time, then it gives rise to computational universality. We give the conditions under which the Hamiltonian given in the proof of Ref. [15] yields gate-set universality. In addition to this, we expand and generalize the proof to include QAOA circuits defined by other classes of cost Hamiltonians. Moreover, we also discuss cases when universality is not reached, which helps to further advance the understanding of limitations of QAOA. For our proofs, we employ techniques from Lie group theory utilized previously in the context of quantum control [18,19,20,21,22,23] and also in proving universality of different families of gate sets [24,25,26,27,28]. In particular, we will make connections with a graph process named zero forcing that was already connected to Lie algebraic controllability questions [29, 30]. Previous works [2, 4, 31] have related controllability to QAOA; our work is continuous in this direction and reveals that there are more fruitful connections to be made between these topics. A recent work by one of the present authors [12] proved that an objective function, expressible in terms of local measurements, can be minimized to prepare arbitrary quantum states as output by quantum circuits. The work, however, assumed the existence of universal variational sequences, such as those needed to realize a universal gate set, but did not prove this reachability. Hence, the sequences developed here would find further applications therein, as well.

The paper is organized as follows. We provide some background to our work in Sect. 2; the QAOA algorithm is introduced together with the notion of universality used in Sect. 2.1 and a brief introduction on quantum control and its relation to QAOA in Sect. 2.3. We then proceed to study the Hamiltonian of Ref. [15] concerning the universality of a 1D QAOA system in Sect. 3. The generalization of the universality proof to other settings is presented in Sects. 4 and 5. Finally, we close with the conclusion and outlook in Sect. 6.

2 Background and setting

Here, we summarize the background of our work. We briefly introduce the concept of QAOA and give the precise definition of universality which is used in this article. Then, we introduce some notation from quantum control and explain how it relates to our proof of the universality of QAOA under certain conditions.

2.1 Quantum approximate optimization algorithm

The quantum approximate optimization algorithm is used to find solutions to combinatorial optimization problems. To introduce the algorithm, we follow the presentation given in [1]. A more complete analysis of the algorithm can be found therein.

The algorithm is defined by a Hamiltonian $H_Z$ encoding the objective function $f:\{0,1\}^n \rightarrow \mathbb {R}$ of a combinatorial optimization problem which we wish to minimize (or alternatively, maximize). This Hamiltonian is assumed to be diagonal in the computational basis and is denoted as the cost Hamiltonian. There is also a second Hamiltonian $H_X$ denoted as mixer Hamiltonian which does not commute with $H_Z$.

First, fix an integer p and 2p random angles $\varvec{\gamma }=(\gamma _1, \gamma _2 \ldots \gamma _p)$, $\varvec{\beta }=(\beta _1,\ldots \beta _p)$. Then, as a subroutine, prepare using a quantum computer an ansatz state

$$\begin{aligned} \left| \varvec{\gamma },\varvec{\beta } \right\rangle =U(H_X,\beta _p)U(H_Z,\gamma _p)\ldots U(H_X,\beta _1)U(H_Z,\gamma _1)\left| + \right\rangle ^{\otimes n} , \end{aligned}$$

(1)

where $U(H,\alpha ) = e^{-i\alpha H}$ and $\left| + \right\rangle = \frac{1}{\sqrt{2}}(\left| 0 \right\rangle + \left| 1 \right\rangle )$. This ansatz state is then measured in the computational basis, which results in a bitstring $z\in \{0,1 \}^n$. We can then evaluate f(z) by sampling enough times from the ansatz state. Then, the following expected value can be approximated

$$\begin{aligned} F_p(\varvec{\gamma },\varvec{\beta }) = \left\langle \varvec{\gamma },\varvec{\beta } \right| H_Z\left| \varvec{\gamma },\varvec{\beta } \right\rangle . \end{aligned}$$

(2)

With a classical optimization algorithm, we seek to minimize this expectation value, and thus, we update the angles $\varvec{\gamma }=(\gamma _1, \gamma _2 \ldots \gamma _p)$, $\varvec{\beta }=(\beta _1,\ldots ,\beta _p)$ for the next round. We repeat this procedure for several rounds.

The operator $H_X$ is usually defined as

$$\begin{aligned} H_X = \sum _{i=1}^{n} X_i, \end{aligned}$$

(3)

where $X_i$ is the usual Pauli matrix acting on the ith qubit.

2.2 Universality of QAOA as a parameterized quantum circuit

To study universality, we need to define what do we mean by it in the context of QAOA. As explained before, QAOA involves a subroutine where a quantum circuit outputs a quantum state. The family of quantum circuits defined by QAOA from a set of angles and a sequence length is given by the product of unitaries in Eq. (1). As discussed in [32], universality in the quantum circuit model is related to the possibility of generating arbitrary unitary operations by composition of elementary gates in a gate set. In this sense, we can consider for a choice of $H_Z$ and $H_X$ the unitaries $U(H_Z,\alpha )$ and $U(H_X,\beta )$ for any angles $\alpha$, $\beta$ as an elementary gate set. Thus, for fixed Hamiltonians $H_Z$, $H_X$ acting on n qubits and $p\in \mathbb {N}_{>0}$ the family of circuits defined by QAOA corresponds to the set of unitaries

$$\begin{aligned} \mathcal {C}_{H_Z,H_X}^{p}{=} \big \{U(H_X,\beta _p)U(H_Z,\gamma _p)\ldots U(H_X,\beta _1)U(H_Z,\gamma _1) | \gamma _j,\beta _j \in \mathbb {R} \big \}, \end{aligned}$$

(4)

where $U(H,\alpha ) = e^{-i\alpha H}$. Thus, we can define

$$\begin{aligned} \mathcal {C}_{H_Z,H_X} = \bigcup _{p=1}^{\infty } \mathcal {C}_{H_Z,H_X}^{p}. \end{aligned}$$

(5)

For a problem size n and a choice of $H_Z$ and $H_X$ acting on n qubits, we say QAOA is universal if any element in the full unitary group $\mathcal {U}(2^n)$ is approximated to arbitrary precision (up to a phase) by an element of $\mathcal {C}_{H_Z,H_X}$.

Note that our definition of universality does not make reference to the sequence length p of Eq. (1). Studying the sequence length at which any unitary in $\mathcal {U}(2^n)$ can be approximated for certain choices of Hamiltonians or even for unitaries in a subspace $\mathcal {A}\subseteq \mathcal {U}(2^n)$ may prove useful in tasks such as state preparation [33, 34], modifications of QAOA where constrains are included [35] or for understanding the limitations of this algorithm [36]. It would also be interesting to investigate universality in other variational quantum algorithms; see Ref. [37] for a recent study in this direction concerning variational quantum eigensolvers.

Finally, let us stress here again that the notion of universality here does not provide an algorithm that finds the solution of the objective function. It just quantifies the reachability properties of QAOA unitary sequences. An analogous notion of universality in classical variational neural networks was given by the universal approximation theorem [38,39,40] which states that under some weak assumptions feed-forward neural networks can approximate any continuous function defined on a compact subset of $\mathbb {R}^k$ without giving an algorithm for the approximation.

2.3 Quantum control

The quantum approximate optimization algorithm can be understood as a particular quantum control problem. Hence, it will be useful to briefly introduce the concept of reachability within quantum control theory.

Let us consider a quantum system with a drift Hamiltonian $H_0$ and assume further that one can turn on or off the Hamiltonians $H_j$ ($j=1, \ldots , n$) with time-dependent coupling strengths (control functions) $u_j$ and in this way obtain the following time-dependent control Hamiltonian

$$\begin{aligned} H(t) = H_0 + \sum _{j=1}^q u_j(t) H_j \, . \end{aligned}$$

(6)

The evolution of the (pure) state of a quantum system is then described by the controlled Schrödinger equation

$$\begin{aligned} i\hbar \frac{\mathrm{d}}{\mathrm{d}t}\left| \psi \right\rangle = H(t) \left| \psi \right\rangle \; , {\text { with initial condition}} \; \; \left| \psi (t=0) \right\rangle = \left| \psi _0 \right\rangle . \end{aligned}$$

(7)

The solution to equation (7) can be written using a unitary propagator $\left| \psi (t) \right\rangle =U(t)\left| \psi _0 \right\rangle$, which can be obtained as the solution to the following differential equation

$$\begin{aligned} \frac{\mathrm{d} }{\mathrm{d} t} U(t) = \left( -iH_0 + \sum _{j=1}^{q} -iu_j(t) H_j \right) U(t) \; \; {\text {with}} \; \; U(0) = \mathbb {1}. \end{aligned}$$

(8)

We want to answer the following question: given a set of control Hamiltonians $\mathcal {P} = \{iH_1, iH_2, \ldots , iH_q\}$, which unitary propagators can we generate?

We assume that the control functions $u_j$ all belong to a set $\mathcal {F}$ of allowed control functions which correspond to piecewise constant functions; this choice will be relevant for QAOA. Before delving more into the problem, let us make some definitions.

Definition 1

(Set of reachable unitaries) Given a quantum system (described by a d-dimensional Hilbert space) with drift Hamiltonian $H_0$ and control Hamiltonians $\{H_j \}_{j=1}^q$, define the set of reachable unitaries at time $T>0$ as the set

$$\begin{aligned} \mathcal {R}(T)=\{ W \in \mathcal {U}(d) : \exists u \in \mathcal {F}, \exists U(t) \; \text {solution of Eq.}~(8), U(T,u) = W\}, \end{aligned}$$

(9)

and the set of reachable unitaries are

$$\begin{aligned} \mathcal {R}&= \overline{\cup _{T>0} \mathcal {R}(T)} \nonumber \\&=\{ W \in \mathcal {U}(d) : \forall \epsilon > 0 \; \exists T_\epsilon \;, \exists U_\epsilon \in \mathcal {R}(T_\epsilon ) \; \text {such that} \; \Vert W- U_\epsilon \Vert \le \epsilon \}, \end{aligned}$$

(10)

where $\Vert \cdot \Vert$ denotes the operator norm.

Definition 2

(Generated Lie Algebra) Given a set of Hamiltonians $\mathcal {P} = \{iH_1, iH_2, \ldots , iH_q\}$, we call the smallest real Lie algebra $\mathcal {L}$ containing the elements of $\mathcal {P}$ the generated Lie algebra of $\mathcal {P}$. We will denote the generated Lie algebra as

$$\begin{aligned} \mathcal {L} = \langle \mathcal {P} \rangle _\mathrm{Lie} = \langle \{iH_1, iH_2, \ldots , iH_q\} \rangle _\mathrm{Lie}. \end{aligned}$$

(11)

Proposition 1

Given a set of Hamiltonian generators $\mathcal {P}$ defining a set of unitary operators according to Eq. (8) (without a drift Hamiltonian $H_0$), then the reachable set of unitaries is the following [41]

$$\begin{aligned} \mathcal {R} = e^{\mathcal {L}} = \{ e^{A_1} e^{A_2} \ldots e^{A_m} : m \in \mathbb {N}, A_j \in \mathcal {L} \}, \end{aligned}$$

(12)

where $\mathcal {L}$ is the Lie algebra generated by $\mathcal {P}$. Moreover, if the quantum system is finite dimensional, we have that $e^{\mathcal {L}}=\{e^{A} : A \in \mathcal {L} \}$.

Proposition 1 motivates us to study the Lie algebra generated by a set of Hamiltonians. To understand whether a set of Hamiltonian interactions $\mathcal {P}$ can generate another set $\mathcal {Q}$, we need to check the condition $\langle \mathcal {P} \rangle _\mathrm{Lie} = \langle \mathcal {P} \cup \mathcal {Q} \rangle _\mathrm{Lie}$.

In the QAOA set-up, we have the control Hamiltonians $H_Z$ and $H_X$, and we are interested in knowing whether the Lie algebra $\mathcal {L} = \langle iH_Z, iH_X \rangle _\mathrm{Lie}$ generates (up to a phase) the entire unitary group $\mathcal {U}(2^n)$. In the examples to follow, we treat families of QAOA gates when universality holds and also mention cases when it does not. Our main proof strategy will be to show either that $e^{\mathcal {L}}$ contains some gates that are already known to form a universal gate set, or that due to some symmetry property we cannot reach all gates.

3 Proving universality in 1D set-up

In [15], a derivation was given for the computational universality of a QAOA where the cost Hamiltonian contained only nearest-neighbour terms on a one-dimensional system (with period-two homogeneous couplings and open boundary conditions). Here, we give the complete proof and the precise conditions under which such a QAOA is universal in the sense of approximating all unitaries.

We start by defining the cost and driver Hamiltonians in a one-dimensional line as in [15],

$$\begin{aligned} H_Z= & {} \sum _j \omega _A Z_{2j} + \omega _B Z_{2j+1} + \gamma _{AB} Z_{2j}Z_{2j+1} + \gamma _{BA} Z_{2j+1} Z_{2j+2} \nonumber \\= & {} \omega _A H_A + \omega _B H_B + \gamma _{AB} H_{AB} + \gamma _{BA} H_{BA}, \end{aligned}$$

(13)

$$\begin{aligned} H_X= & {} \sum _j X_j. \end{aligned}$$

(14)

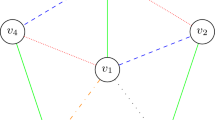
We shall prove that when the number of qubits n is odd, the QAOA defined with the previous Hamiltonians is universal. For the n even case, we will see this is not the case. A graph representing the Hamiltonian $H_Z$ for $n=6$ is shown in Fig. 1.

Fig. 1

System corresponding to Hamiltonian in Eq. (13) for $n=6$. Each node corresponds to qubits in the system and the edges to a two-body interaction

For clarity, we make explicit the limits of the sums for each term in $H_Z$. Furthermore, we write in the upper limits of the sums the corresponding limits for n even | n odd.

$$\begin{aligned} H_A&= \sum _{j=1}^{ \frac{n}{2} | \frac{n-1}{2}} Z_{2j},&H_B&= \sum _{j=0}^{\frac{n}{2} -1 | \frac{n-1}{2}} Z_{2j+1}, \end{aligned}$$

(15)

$$\begin{aligned} H_{AB}&= \sum _{j=1}^{\frac{n}{2} -1 | \frac{n-1}{2}} Z_{2j} Z_{2j+1},&H_{BA}&= \sum _{j=0}^{\frac{n}{2} -1 | \frac{n-3}{2}} Z_{2j+1} Z_{2j+2},\end{aligned}$$

(16)

$$\begin{aligned} H_X&= \sum _{j=1}^{n} X_j. \end{aligned}$$

(17)

It will also be useful to define

$$\begin{aligned} X_{\mathrm {odd}}&= \sum _{j=0}^{\frac{n}{2}-1 | \frac{n-1}{2}} X_{2j+1},&X_{\mathrm {even}}&= \sum _{j=1}^{\frac{n}{2} | \frac{n-1}{2}} X_{2j}. \end{aligned}$$

(18)

To prove the universality on this model, we shall prove that all one-qubit Pauli operators are in the Lie algebra $\{iH_Z, iH_X \} \rangle _\mathrm{Lie}$, which implies that all one-qubit gates can be generated as consequence of Proposition 1. We will also prove that the $\mathrm {CNOT}$ gate can be generated by elements in the Lie algebra. With this, we conclude that any unitary can be generated with enough depth on the QAOA sequence. This proves the existence of such QAOA sequence but does not give a particular set of angles to obtain the unitary, neither will we study the efficiency of the method which we leave as an open problem for future work. We will start by proving the following lemma which allows to separate the quadratic and linear terms on $H_Z$.

Lemma 1

$iH_{Z1}=\omega _A iH_A + \omega _B iH_B \in \mathcal {L} =\langle \{iH_Z, iH_X \} \rangle _\mathrm{Lie}$. Note that as a consequence, we have that $iH_{Z2} = \gamma _{AB} iH_{AB} + \gamma _{BA} iH_{BA} \in \mathcal {L}$

Proof

Consider first the commutator

$$\begin{aligned} \begin{aligned} H_{YZ} = \frac{1}{2i}[H_Z,H_X]&= \omega _A \sum _{j=1}^{\frac{n}{2} | \frac{n-1}{2}} Y_{2j} + \omega _B \sum _{j=1}^{\frac{n}{2}-1 | \frac{n-1}{2}} Y_{2j+1} \\&\quad + \gamma _{AB} \sum _{j=1}^{\frac{n}{2}-1 | \frac{n-1}{2}} (Y_{2j}Z_{2j+1} + Z_{2j}Y_{2j+1})\\&\quad + \gamma _{BA} \sum _{j=0}^{\frac{n}{2}-1 | \frac{n-3}{2}} (Y_{2j+1}Z_{2j+2} + Z_{2j+1}Y_{2j+2}), \\ \end{aligned} \end{aligned}$$

(19)

and then, let us perform the calculation

$$\begin{aligned} \begin{aligned} \frac{1}{2i}[H_{YZ}, H_X]&= -\omega _A \sum _{j=1}^{\frac{n}{2} | \frac{n-1}{2}} Z_{2j} - \omega _B \sum _{j=1}^{\frac{n}{2}-1 | \frac{n-1}{2}} Z_{2j+1}\\&\quad + \gamma _{AB} \sum _{j=1}^{\frac{n}{2}-1 | \frac{n-1}{2}} 2(Y_{2j} Y_{2j+1} - Z_{2j}Z_{2j+1})\\&\quad \quad + \gamma _{BA} \sum _{j=0}^{\frac{n}{2}-1 | \frac{n-3}{2}} 2(Y_{2j+1}Y_{2j+2} - Z_{2j+1}Z_{2j+2}), \\ \end{aligned} \end{aligned}$$

(20)

and define

$$\begin{aligned} \begin{aligned} H_{(1)}&= \frac{1}{2i}[H_{YZ},H_X] + H_Z\\&= 2\gamma _{AB} \sum _{j=1}^{\frac{n}{2}-1 | \frac{n-1}{2}} Y_{2j} Y_{2j+1} + 2\gamma _{BA} \sum _{j=0}^{\frac{n}{2}-1 | \frac{n-3}{2}} Y_{2j+1}Y_{2j+2}\\&\quad - \gamma _{AB} \sum _{j=1}^{\frac{n}{2}-1 | \frac{n-1}{2}} Z_{2j}Z_{2j+1} - \gamma _{BA} \sum _{j=0}^{\frac{n}{2}-1 | \frac{n-3}{2}} Z_{2j+1}Z_{2j+2}. \end{aligned} \end{aligned}$$

(21)

Next, define also

$$\begin{aligned} \begin{aligned} H_{(2)}&= \frac{1}{2i}[H_{(1)},H_X] \\&= -3\gamma _{AB} \sum _{j=1}^{\frac{n}{2}-1 | \frac{n-1}{2}} (Y_{2j} Z_{2j+1} + Z_{2j} Y_{2j+1})\\&\quad - 3\gamma _{BA} \sum _{j=0}^{\frac{n}{2}-1 | \frac{n-3}{2}} (Y_{2j+1} Z_{2j+2} + Z_{2j+1} Y_{2j+2}). \end{aligned} \end{aligned}$$

(22)

Finally, notice that we have

$$\begin{aligned} \frac{1}{2i}\left[ H_{YZ} + \frac{1}{3} H_{(2)} , H_X\right] = H_{Z2}. \end{aligned}$$

(23)

Thus, we find that $iH_{Z2} \in \mathcal {L}$ and we can subtract this from $iH_Z$, implying that $iH_{Z1} \in \mathcal {L}$, which completes the proof. $\square$

Next, we prove that it is possible to generate $X_\mathrm{even}$ and $X_\mathrm{odd}$

Proposition 2

Let $\omega _A^2 \ne \omega _B^2$, then $iX_\mathrm{even}$, $iX_\mathrm{odd}$$\in \mathcal {L} = \langle iH_Z, iH_X \rangle _\mathrm{Lie}$

Proof

From Lemma 1, we have that $iH_{Z1} = \omega _A iH_A + \omega _B iH_B$, $iH_{Z2} = \gamma _{AB} iH_{AB} + \gamma _{BA} iH_{BA}$$\in \mathcal {L}$.

Next, let us define the following element in the Lie algebra

$$\begin{aligned} \begin{aligned} H_{Y1}&= \frac{1}{2i}[H_{Z1}, H_{X}] \\&= \omega _A \sum _{j=1}^{\frac{n}{2} | \frac{n-1}{2}} Y_{2j} + \omega _B \sum _{j=0}^{\frac{n}{2}-1 | \frac{n-1}{2}} Y_{2j+1}, \end{aligned} \end{aligned}$$

(24)

and then calculate the commutator

$$\begin{aligned} \begin{aligned} \frac{1}{2i}[H_{Z1},H_{Y1}]&= \omega _A^2 \sum _{j=1}^{\frac{n}{2} | \frac{n-1}{2} } X_{2j} + \omega _B^{2} \sum _{j=0}^{\frac{n}{2}-1 | \frac{n-1}{2} } X_{2j+1}. \end{aligned} \end{aligned}$$

(25)

Now notice that

$$\begin{aligned} \begin{aligned} \omega _A^2 H_X - \omega _A^2 \sum _{j=1}^{\frac{n}{2} | \frac{n-1}{2} } X_{2j} - \omega _B^{2} \sum _{j=0}^{\frac{n}{2}-1 | \frac{n-1}{2} } X_{2j+1} = (\omega _A^2 - \omega _B^2) \sum _{j=0}^{\frac{n}{2}-1 | \frac{n-1}{2} } X_{2j+1}, \end{aligned} \end{aligned}$$

(26)

which implies that if $\omega _A^2 \ne \omega _B^2$, then $iX_\mathrm{even}$, $iX_\mathrm{odd}$$\in \mathcal {L}$. $\square$

From what we have so far proved, we can then generate $H_A, H_B, H_{AB}, H_{BA}$. The following proposition states the conditions for this.

Proposition 3

Assume $\gamma _{AB}^2 \ne \gamma _{BA}^2$ and let $\gamma = (\gamma _{AB}^2 - 4\gamma _{BA}^2)$. If $\gamma \ne 0$, $\gamma _{AB}^2 \ne 0$, $\gamma _{BA}^2 \ne 0$, then $iH_A$, $iH_B$, $iH_{AB}$, $iH_{BA} \in \langle iH_Z, iH_X \rangle _\mathrm{Lie}$.

The proof of Proposition 3 is given in “Appendix A”. Note that in Ref. [15] it was required that $\omega _A, \omega _B, \gamma _{AB}, \gamma _{BA}$ be rationally independent. In our proof of universality, this will be relaxed to the condition given by Proposition 3.

In the following, we will prove that when n is odd and the condition of the previous lemmas and propositions is fulfilled, QAOA can implement all one-qubit operators and CNOT.

Lemma 2

Assuming n is odd, then $iX_j \in \langle iH_A, iH_B, iH_{AB}, iH_{BA}, iH_X \rangle _\mathrm{Lie}$ for any $j \in \{1, \ldots , n\}$.

The proof of Lemma 2 is given in “Appendix A”.

Theorem 1

Given an odd integer n, $H_Z$ as in Eq. (13), $H_X$ as in Eq. (14), with coefficients in $H_Z$ and $H_X$ fulfilling the conditions of Proposition 3 and $\mathcal {L} =\langle iH_Z, iH_X \rangle _\mathrm{Lie}$, then $e^{\mathcal {L}}$ is dense in $\mathcal {U}(n)$. This implies universality for odd integers in QAOA.

Proof

We proved in Lemma 2 that $R_X(\theta ) = e^{\frac{i}{2}X \theta } \in e^{\mathcal {L}}$ it is easy to see that also $R_Y(\phi ), R_Z(\psi ) \in e^{\mathcal {L}}$. Thus, all single qubit operators are in $e^{\mathcal {L}}$. If it is possible to generate a two qubit gate such as CNOT, then we can prove that $\mathcal {L}$ can generate any unitary by, for example, generating the gate set of Clifford gates + T, which are known to be universal for quantum computation. In fact, any two-qubit entangling operator with all one-qubit gates is enough for universality [24].

In the proof of Lemma 2, we have managed to generate not only one-qubit Pauli’s but also two-qubit Pauli’s such as $Z_{k-1} Z_k$. To see that CNOT gates can be generated, recall that $CNOT = {\vert 0\rangle \!\langle 0\vert } \otimes \mathbb {1}+ {\vert 1\rangle \!\langle 1\vert } \otimes X = \frac{1}{2} ( \mathbb {1}\otimes \mathbb {1}+ Z \otimes \mathbb {1}+ \mathbb {1}\otimes X - Z \otimes X )$. Note that this last expression is in $\mathcal {L}$.

Finally, note that

$$\begin{aligned} \begin{aligned} e^{i\frac{\pi }{4} (\mathbb {1}\otimes \mathbb {1}- \mathbb {1}\otimes X - Z \otimes \mathbb {1}+ Z \otimes X)}&= e^{i\frac{\pi }{4} (1-\mathbb {1}\otimes X)(1 - Z \otimes \mathbb {1})}\\&= CNOT. \end{aligned} \end{aligned}$$

(27)

Since $\mathbb {1}\otimes \mathbb {1}- X_2 - Z_1 + Z_1 X_2$ is in $\mathcal {L}$, we conclude that CNOT can be generated. $\square$

With this, we have proved universality for n odd. It is easy to see that for n even $\langle iH_Z, iH_X \rangle _\mathrm{Lie}$ cannot approximate $\mathcal {U}(2^n)$ due to the presence of a symmetry in the system. This is easier to see with a concrete example, if $n=4$ and we number qubits from 1 to 4 then exchanging qubit 1 with qubit 4 and exchanging qubit 2 with qubit 3 is a symmetry of the system. The presence of a symmetry in Hamiltonians $H_Z$ and $H_X$ implies non-universality; let U be the unitary implementing the symmetry commuting with both Hamiltonians; then, $H_Z$ and $H_X$ can be block diagonalized, which necessarily implies that there are elements in $\mathcal {U}(2^n)$ that cannot be approximated. Note nonetheless that for n even, we can just add an extra qubit to obtain universality.

4 Universality for QAOA defined on graphs

In Sect. 3, we prove universality in a particular setting of a QAOA. Here, we show that universality can be obtained also in more general settings. The algorithms defined here are characterized by the choice of the Hamiltonians $H_Z$ and $H_X$. To define $H_Z$, we make a correspondence between a non-directed simple graph (no loops or multiple edges) $G=(V,E)$ and the terms appearing in $H_Z$, while the Hamiltonian $H_X$ is defined as in Sect. 3.

4.1 Universality from zero forcing

We prove in this section that the property of universality on this class of QAOA is present depending on a process defined on the graph G called zero forcing. The notion of zero forcing has been presented before in the context of quantum control on graphs [29, 30, 42], and we find that it applies as well in this context.

Definition 3

(Zero forcing) Consider a simple graph $G=(V,E)$, a zero forcing process on G consists of an initial set of vertices $S \subseteq V$ which we will consider as “infected”. The rest of the vertices are non-infected. Then, we proceed by steps to infect other nodes; at each step, an infected vertex v infects a non-infected neighbour w if w is the only non-infected neighbour of v. We call S a zero forcing set if we can infect all the graphs by starting with all infected vertices in S.

Fig. 2

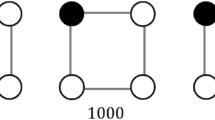
Example of a zero forcing process on a graph. The initial set of infected vertices S is shown in red in (a); the rest of nodes are uninfected initially. At any step, a given node that has a unique non-infected neighbour infects such neighbour. At each step, we color red the corresponding infected nodes (Color figure online)

An example of a zero forcing process is shown in Fig. 2. As usual with QAOA, we start defining two Hamiltonians $H_Z$ and $H_X$. Consider simple graph $G=(V,E)$ and a subset $S \subseteq V$.

$$\begin{aligned} H_Z= & {} \gamma \sum _{(i,j) \in E} Z_i Z_j + \sum _{i\in S} \omega _i Z_i + \omega \sum _{i \in V \setminus S} Z_i\nonumber \\= & {} \gamma H_{\gamma } + \sum _{i\in S} \omega _i Z_i + \omega H_V, \end{aligned}$$

(28)

$$\begin{aligned} H_X= & {} \sum _{i\in V} X_i. \end{aligned}$$

(29)

Theorem 2

Let $G=(V,E)$ be a simple graph and $S\subseteq V$. Define $H_Z$ and $H_X$ as in Eqs. 28 and 29 and let $\gamma$, $\omega _i$, $\omega$ be rationally independent. Consider S as the initial set of infected nodes in a zero forcing process. If S is a zero forcing set, then $Z_k Z_j \in \langle H_Z, H_X \rangle _\mathrm{Lie}$ for all $(k,j) \in E$ and $X_k \in \langle H_Z, H_X \rangle _\mathrm{Lie}$ for all $k \in V$.

Proof

Since $\gamma$, $\omega _i$, $\omega$ are rationally independent, using a similar method to the proof in Proposition 4 (see “Appendix B”) we can generate $H_\gamma , H_V, Z_i$ for $i \in S$. First, note that for vertices $i \in S$ we can generate $X_i$. Consider two vertices $i,j \in S$ such that they are neighbouring vertices in G. To see this, commute

$$\begin{aligned} \frac{1}{(2i)^2}[[H_\gamma ,X_i],X_j]= Y_i Y_j. \end{aligned}$$

(30)

Thus, we can also generate $Z_i Z_j$. Consider now $i\in S$ that only has one neighbour $j\in V\setminus S$. We show that we can generate $X_j$. Define $H_i$ as $H_\gamma$ with the interaction terms corresponding to infected neighbours of i subtracted. Consider now the commutator:

$$\begin{aligned} \frac{1}{2i}[X_i,H_i] = Y_i Z_j . \end{aligned}$$

(31)

And thus, $Z_i Z_j$ can be generated. Then, we can commute with $H_X - X_i$ and generate $Z_i Y_j$ which commuted with $Z_i Z_j$ generates $X_j$. This is analogous to an infection step in the zero forcing process. It is then easily seen that if S is zero forcing, then all one-qubit and two-qubit operators are generated in the graph. $\square$

We can generalize even more this zero forcing process by difference considering edge interactions in $H_Z$. Given once again a graph $G=(V,E)$ and set $S\subseteq V$, consider now that we can partition the set of edges E into q disjoint sets $\{E_i\}_{i\in [q]}$ such that $\bigcup _{i\in [q]} E_i = E$. From this, we write the Hamiltonian

$$\begin{aligned} \begin{aligned} H_Z&= \sum _{k=1}^q \sum _{(i,j) \in E_k} \gamma _k Z_i Z_j + \sum _{i\in S} \omega _i Z_i + \omega \sum _{i \in V \setminus S} Z_i\\&=\sum _{k=1}^q \gamma _k H_{\gamma _k} + \sum _{i\in S} \omega _i Z_i + \omega H_V. \end{aligned} \end{aligned}$$

(32)

Definition 4

(Generalized zero forcing for multi-type edges) Consider a simple graph $G=(V,E)$ with $E=\bigsqcup _{i\in [q]} E_i$, a zero forcing process on G consists of an initial set of vertices $S \subseteq V$ which we will consider as “infected”. The rest of the vertices are non-infected.

The generalized zero forcing process proceeds in one step by considering each infected vertex and the subgraph $G_1 =(V,E_1)$. If an infected vertex has a single non-infected vertex in $G_1$, then infect this new vertex and add it to S. Then, proceed in the same fashion with the neighbours of vertices on S in graphs $G_2,G_3,\ldots ,G_q$. Repeat this process, and if the whole graph ends infected, then we call the initial set S a generalized zero forcing set.

We prove the following result.

Theorem 3

Let $G=(V,E)$ be a simple graph, $S\subseteq V$ and consider a partition of the set of edges E into q disjoint sets $\{E_i\}_{i\in [q]}$ such that $\bigcup _{i\in [q]} E_i = E$. Define $H_Z$ and $H_X$ as in Eqs. (32) and (29) and let $\gamma$, $\omega _i$, $\omega$ be rationally independent. Consider S as the initial set of infected nodes in a zero forcing process. If S is a generalized zero forcing set, then $\langle H_Z, H_X \rangle$ generates $Z_k Z_j$ for all $(k,j) \in E$ and $X_k$ for all $k \in V$.

Proof

The proof is almost the same as in Theorem 2. $\square$

4.2 Universality without zero forcing

Note that a Hamiltonian defined from a graph and an initial subset of vertices S may not have a zero forcing set, yet nonetheless can be universal. We will give one such an example with a two-dimensional grid with only two edges under control, meaning that the coupling constant for linear and quadratic terms of the Hamiltonian including the edges and nodes in control is different than for the other terms in the Hamiltonian. This example points to a more general process than zero forcing that allows to study universality in the corresponding QAOA, although we will not pursue this direction in this work.

Define a graph composed of a square grid with $N = n^2$ vertices, number the vertices from $v_1$ to $v_N$ left to right and top to bottom . We assume all interactions in the grid are labelled by the same interaction type A. We also add two extra nodes labelled $v_{N+1}$ and $v_{N+2}$. Connect $v_{N+1}$ to vertex $v_{1}$ with an edge labelled B and connect $v_{N+2}$ to $v_{N}$ with an edge labelled C. We give an example for $N=25$ in Fig. 3.

For this graph, we define the following Hamiltonians:

$$\begin{aligned} H_Z= & {} \omega _A \sum _{v_i \in V_{Grid}} Z_{v_i} + \omega _B Z_{v_{N+1}} + \omega _C Z_{v_{N+2}}\nonumber \\&+ \gamma _{A} \sum _{(v_i,v_j)\in E_{Grid}} Z_{v_i} Z_{v_j} + \gamma _{B} Z_{v_{1}} Z_{v_{N+1}} + \gamma _{C} Z_{v_{n}} Z_{v_{N+2}}, \end{aligned}$$

(33)

$$\begin{aligned} H_X= & {} \sum _{i=1}^{N+2} X_i. \end{aligned}$$

(34)

Fig. 3

Grid with $N=25$ nodes which defines a Hamiltonian as in Eq. (33). Vertices 26 and 27 correspond to qubits where $H_Z$ acts with one-qubit operators with coefficients $\omega _B$ and $\omega _C$, the corresponding incident edges define two-qubit interactions with coefficients $\gamma _B$ and $\gamma _C$ (color online)

We want to prove that every one-qubit operator $Z_i$ and two body operators $Z_i Z_j$ can be generated.

Note that Lemma 1 applies in this situation as well, so we can separate

$$\begin{aligned} H_{Z1}= & {} \omega _A H_{A1} + \omega _B Z_{N+1} + \omega _C Z_{N+1},\\ H_{Z2}= & {} \gamma _A H_{A2} + \gamma _B Z_{v_{1}} Z_{v_{N+1}} + \gamma _C Z_{v_{n}} Z_{v_{N+2}}. \end{aligned}$$

From this, we easily see that we can generate as well $X_{N+1}$, $X_{N+2}$ and $X_{Grid} = \sum _{i=1}^{N} X_i$. Finally, notice that generating $H_{A1}$, $Z_{N+1}$, $Z_{N+1}$, $H_{A2}$, $Z_{v_{1}} Z_{v_{N+1}}$, $Z_{v_{n}} Z_{v_{N+2}}$ separately can be done by applying Proposition 4.

To prove that any gate can be generated with these Hamiltonians, we prove that all $Z_j$ with $j\in \{1,\ldots ,n\}$ and $Z_k Z_{k+1}$ with $k \in \{1,\ldots ,n-1\}$ can be generated. In this way, there is full controllability of the first horizontal line in the grid. After proving this, it directly follows that QAOA defined from the grid is universal by the zero forcing argument.

Theorem 4

Given a graph G as described above, vertices numbered in the order mentioned previously, and given the Hamiltonians $H_{A1}$, $Z_{N+1}$, $Z_{N+2}$, $X_{N+1}$, $X_{N+2}$, $X_{Grid}$, $H_{A2}$, $Z_{1} Z_{N+1}$, $Z_{n} Z_{N+2}$, then for $i\in \{1,\ldots ,n-1\}$ and $j\in \{1,\ldots ,n\}$ we have that $Z_j$, $X_j$ ,$Z_i Z_{i+1} \in \langle H_{A1}$, $Z_{N+1}$, $Z_{N+1}$, $H_{A2}$, $Z_{1} Z_{N+1}$, $Z_{n} Z_{N+2}\rangle _\mathrm{Lie}$. This implies universality for any n on the grid.

The proof is given in “Appendix C”. As mentioned before, this points to a more general process that allows to show universality but for brevity we will not go further in this direction.

5 Universality for QAOA defined on hypergraphs

So far, the Hamiltonians $H_Z$ induced by graphs define only quadratic or linear terms. We can consider higher-order terms for $H_Z$ by studying a modified version of a zero forcing process on hypergraphs. Here, we will consider the specific case of Hamiltonians with cubic terms as there is already work studying problems with cubic-order term Hamiltonians as in the MAXE3LIN2 problem [43].

From a hypergraph, we can define Hamiltonians $H_Z$ with k-body terms where $k>2$. A hypergraph $\mathcal {G}=(V,E)$ is a generalization of a graph, and it is defined by a finite set of vertices V and a finite set E which contains non-empty subsets of V which are called hyperedges. In Fig. 4, we show an example of a hypergraph defined by $V=\{v_1,v_2,\ldots ,v_6\}$ and

$$\begin{aligned} E=\bigg \{ \{v_1,v_2,v_3 \}, \{v_2, v_3, v_4 \}, \{v_3, v_4, v_5 \}, \{v_4, v_5, v_6 \} \bigg \}. \end{aligned}$$

This is also an example of a 3-uniform hypergraph; a k-uniform hypergraph is one where all hyperedges have exactly k nodes.

Fig. 4

Example of a 3-uniform hypergraph on a line where by definition every hyperedge contains three edges (color online)

We will prove here universality on 3-uniform hypergraphs with a small modification in the Hamiltonian defined from the hypergraph. Consider a hypergraph $\mathcal {G}=(V,E)$ with $V=\{1,\ldots ,n\}$ and $E=\bigg \{\{1,2 \}, \{1,2,3\},\{2,3,4\},\ldots ,\{n-2,n-1,n\} \bigg \}$. An example for $n=6$ is shown in Fig. 4 (without the 2-edge).

From $\mathcal {G}$, we define the following Hamiltonians

$$\begin{aligned} H_Z= & {} \delta \sum _{\{i,j,k\} \in E} Z_i Z_j Z_k + \gamma Z_1 Z_2 + \omega _1 Z_1 + \omega \sum _{i \ne 1} Z_i\nonumber \\= & {} \delta H_{\delta } + \gamma Z_1 Z_2 + \omega _1 Z_1 + \omega H_V, \end{aligned}$$

(35)

$$\begin{aligned} H_X= & {} \sum _{i\in V} X_i. \end{aligned}$$

(36)

We wish to generate all two-qubit operators between neighbours and one-qubit operators on every vertex. This hyper-zero forcing is defined by starting with some initial set of infected vertices $S_1$ and a set of infected 2-edges $S_2$; at each step, pick an infected vertex; if it has only one non-infected 3-neighbour, then infect the neighbour. If it has two infected 3-neighbours, share a 2-edge and then connect each infected node to the non-infected one with 2-edges.

In the 3-uniform hypergraph, the infection step in terms of the commutators proceeds as follows: first note that the term $Z_1 Z_2 Z_3$ can be separated from the other cubic terms and that $X_2$ can be easily separated; now consider

$$\begin{aligned} \frac{1}{2i}[Z_1 Y_2, Z_1 Z_2 Z_3] = X_2 Z_3. \end{aligned}$$

(37)

From this, we see that $X_3$ can be separated and we can proceed to separate $Z_2 Z_3 Z_4$. In this way, we proceed until the end of the chain having produced all one-qubit and two-qubit operators between neighbours which proves universality.

We can define a hyper-zero forcing procedure on hypergraphs which allows to check whether the corresponding QAOA is universal. We will write here for conciseness only the case of hypergraphs with hyperedges with at most three elements although a more generalized version is possible

Definition 5

Consider a hypergraph $\mathcal {G}=(V,E)$ where $|e|\le 3$ for all $e \in E$; a hyper-zero forcing process on $\mathcal {G}$ consists of an initial set of vertices $S_1 \subseteq V$ and an initial set of 2-edges $S_2$ which we will consider as “infected”. The rest of the vertices and 2-edges are non-infected. Then, we proceed by steps to infect other nodes; at each step, a pair of infected vertices $v_1, v_2$ infects a non-infected 3-neighbour w if w is the only non-infected 3-neighbour of $v_1$ and $v_2$ and also the 2-edge ${v_1, v_2}$ is infected. We call $S_1$ and $S_2$ hyper-zero forcing sets if we can infect all the graphs by starting with $S_1$ and $S_2$ infected.

An analogous theorem can be derived as in the zero forcing case for relating hyper-zero forcing processes and universality. Here, for simplicity, we state such theorem for hypergraphs with hyperedges containing three or less vertices.

Theorem 5

Let $\mathcal {G}=(V,E)$ be a hypergraph with $|e| \le$, $S_1 \subseteq V$ and $S_2$ a set of 2-edges. Define $H_Z$ and $H_X$ as in Eqs. 35 and 36 and let all coefficients in $H_Z$ be rationally independent. Consider $S_1$ as the initial set of infected nodes and $S_2$ as the set of infected edges in a hyper-zero forcing process. If $S_1$ and $S_2$ are hyper-zero forcing sets, then $Z_k Z_j \in \langle H_Z, H_X \rangle _\mathrm{Lie}$ for all $(k,j) \in E$ and $X_k \in \langle H_Z, H_X \rangle _\mathrm{Lie}$ for all $k \in V$.

Proof

Proof follows directly from arguments in the 3-uniform hypergraph case and similarly as in the zero process case. $\square$

In a previous work [26], it was shown that local unitaries and unitaries generated by three-body Pauli operators do not give rise to universality. This directly implies the following no-go result:

Theorem 6

Define $H_Z$ and $H_X$ as in Eqs. 35 and 36. If the coefficient $\gamma$ in $H_Z$ is zero, then the QAOA defined by $H_Z$ and $H_X$ does not yield a universal gate set.

6 Conclusion and outlook

We proved the universality of different QAOA set-ups. In particular, we completed an earlier proof of computational universality for a specific set-up given in Ref. [15] and also found two new broad classes of driver Hamiltonians that allow the corresponding QAOA unitaries to approximate any unitary. The first class consists of Hamiltonians with quadratic and linear terms; the quadratic terms are distributed according to the adjacency matrix of a graph, while the coupling strength of the linear terms is grouped into two parts defined by a so-called zero forcing set of the graph. This construction was then generalized to obtain a second class of driver Hamiltonians with higher-order terms corresponding to hypergraphs and generalized zero forcing sets. Here, it should also be mentioned that the square grid example, presented in Sect. 4.2, points to a more general graph process different from zero forcing that may further advance an understanding of universality in QAOA circuits (and perhaps also in more general quantum control set-ups). Another important generalization of our results would be to regard other mixer Hamiltonians and then the type $H_X = \sum _i X_i$ considered here, e.g. one could consider XY mixers [35, 44]. One could hope to determine more general conditions for universality of QAOA unitaries, which could include the above-mentioned generalizations; we leave this for future work. Such general results could help in understanding the relation between the choice of Hamiltonians and the space reached by the ansatz in the algorithm, and perhaps also to obtain some analytical results about the efficiency of QAOA. We regard our work as a first step towards this goal.

Appendices

Appendix

Proof of some results in Sect. 3

Proposition 3. Assume $\gamma _{AB}^2 \ne \gamma _{BA}^2$and let $\gamma = (\gamma _{AB}^2 - 4\gamma _{BA}^2)$.If $\gamma \ne 0$, $\gamma _{AB}^2 \ne 0$, $\gamma _{BA}^2 \ne 0$, then $iH_A$, $iH_B$, $iH_{AB}$, $iH_{BA} \in \langle iH_Z, iH_X \rangle _\mathrm{Lie}$.

Proof

From Proposition 2, we see that $H_A$ and $H_B$ can be easily generated. To prove that $H_{AB}$ and $H_{BA}$ can be generated, we separate the proof for n odd and n even case.

$\underline{n}$odd:

$$\begin{aligned} \begin{aligned} {[}H_{Z2}, X_{\mathrm {even}}]&= \gamma _{AB} \sum _{j=1}^{\frac{n-1}{2}} Y_{2j} Z_{2j+1} + \gamma _{BA} \sum _{j=0}^{\frac{n-3}{2}} Z_{2j+1} Y_{2j+2}\\&= H_{YZ}^{e}. \end{aligned} \end{aligned}$$

(38)

Then,

$$\begin{aligned} \begin{aligned} {[}H_{YZ}^{e} , H_{Z2}]&= \gamma _{AB}^2 \sum _{j=1}^{\frac{n-1}{2}} X_{2j} + 2\gamma _{AB} \gamma _{BA} \sum _{j=1}^{\frac{n-1}{2}} Z_{2j-1}X_{2j}Z_{2j+1}\\&\quad + \gamma _{BA}^2 \sum _{k=0}^{\frac{n-3}{2}} X_{2j+2}. \end{aligned} \end{aligned}$$

(39)

Note that we have suppressed the (2i) that appears from the commutators. The $\gamma _{AB}^2$ and $\gamma _{BA}^2$ terms in the last line can be removed, so we define

$$\begin{aligned} H_{ZXZ} = \sum _{j=1}^{\frac{n-1}{2}} Z_{2j-1}X_{2j}Z_{2j+1}. \end{aligned}$$

Consider now

$$\begin{aligned} \begin{aligned} {[}H_{YZ}^{e}, H_{ZXZ}]&= \gamma _{AB} \sum _{j=1}^{\frac{n-1}{2}} Z_{2j-1}X_{2j} + \gamma _{BA} \sum _{j=1}^{\frac{n-1}{2}} X_{2j} Z_{2j+1},\\ \end{aligned} \end{aligned}$$

(40)

and define

$$\begin{aligned} H_{Z',2}^{\mathrm {odd}} = \gamma _{AB} \sum _{j=1}^{\frac{n-1}{2}} Z_{2j-1}X_{2j} + \gamma _{BA} \sum _{j=1}^{\frac{n-1}{2}} X_{2j} Z_{2j+1}. \end{aligned}$$

Notice that

$$\begin{aligned} \begin{aligned} \gamma _{AB} H_{Z',2}^{\mathrm {odd}} - \gamma _{BA} H_{Z2} = (\gamma _{AB}^2 - \gamma _{BA}^2) \sum _{j=0}^{\frac{n-3}{2}} Z_{2j+1}Z_{2j+2}. \end{aligned} \end{aligned}$$

(41)

Thus, assuming $\gamma _{AB}^2 \ne \gamma _{BA}^2$ then we have generated $H_{AB}$ and $H_{BA}$ for odd n.

$\underline{n}$even:

Following steps analogous to the odd n case, we obtain

$$\begin{aligned} {[}H_{Z2}, X_{\mathrm {odd}}]= & {} \gamma _{AB} \sum _{j=1}^{\frac{n}{2}-1} Z_{2j} Y_{2j+1} + \gamma _{BA} \sum _{j=0}^{\frac{n}{2}-1} Y_{2j+1} Z_{2j+2}\nonumber \\&= H_{YZ}^{oo}, \end{aligned}$$

(42)

$$\begin{aligned} {[}H_{YZ}^{oo}, H_{Z2}]= & {} \gamma _{AB}^2 \sum _{j=1}^{\frac{n}{2}-1} X_{2k+1} + 2\gamma _{AB} \gamma _{BA} \sum _{j=1}^{\frac{n}{2}-1} Z_{2j} X_{2j+1}Z_{2j+2} \nonumber \\&\quad + \gamma _{BA}^2 \sum _{j=0}^{\frac{n}{2}-1} X_{2k+1}. \end{aligned}$$

(43)

The last line is true up to a (2i) factor. In the last line, we can also eliminate the $\gamma _{BA}^2$ and define

$$\begin{aligned} H_{ZZZ1}= & {} -\gamma _{AB} Z_1 + 2\gamma _{BA} \sum _{j=1}^{\frac{n}{2}-1} Z_{2j}Z_{2j+1}Z_{2j+2},\nonumber \\ {[}H_{YZ}^{oo},H_{ZZZ1}]= & {} 2\gamma _{AB} \sum _{j=1}^{\frac{n}{2}-1} Z_{2j+1} Z_{2j+2} -\gamma _{AB} Z_1 Z_2 + 2\gamma _{BA} \sum _{j=1}^{\frac{n}{2}-1} Z_{2j} Z_{2j+1}= H_{12}.\nonumber \\ \end{aligned}$$

(44)

Now we perform a similar calculation but using $X_\mathrm{even}$.

$$\begin{aligned} {[}H_{Z2},X_{\mathrm {even}}]= & {} \gamma _{AB} \sum _{j=1}^{\frac{n}{2}-1} Y_{2j} Z_{2j+1} +\gamma _{BA} \sum _{j=0}^{\frac{n}{2}-1} Z_{2j+1} Y_{2j+2}\nonumber \\= & {} H_{YZ}^{ee}, \end{aligned}$$

(45)

$$\begin{aligned} {[}H_{YZ}^{ee},H_{Z2}]= & {} \gamma _{AB}^2 \sum _{j=1}^{\frac{n}{2}-1} X_{2j} + 2\gamma _{AB} \gamma _{BA} \sum _{j=1}^{\frac{n}{2}-1} Z_{2j-1}X_{2j}Z_{2j+1}\nonumber \\&+ \gamma _{BA}^2 \sum _{j=0}^{\frac{n}{2}-1} X_{2j+2}. \end{aligned}$$

(46)

We can remove the $\gamma _{BA}^2$ and define

$$\begin{aligned} H_{ZZZn}= & {} -\gamma _{AB}Z_{n} + 2\gamma _{BA} \sum _{j=1}^{\frac{n}{2}-1} Z_{2j-1}X_{2j} Z_{2j+1},\nonumber \\ {[}H_{YZ},H_{ZZZn}]= & {} 2\gamma _{AB}\gamma _{BA} \sum _{j=1}^{\frac{n}{2}-1} Z_{2j-1}X_{2j} - \gamma _{BA} \gamma _{AB} Z_{n-1}X_{n} +2 \gamma _{BA}^2 \sum _{j=1}^{\frac{n}{2}-1} X_{2j} Z_{2j+1}.\nonumber \\ \end{aligned}$$

(47)

Thus, we define

$$\begin{aligned} H_{n-1,n} = 2\gamma _{AB} \sum _{j=1}^{\frac{n}{2}-1} Z_{2j-1}Z_{2j} - \gamma _{AB} Z_{n-1}X_{n} +2 \gamma _{BA} \sum _{j=1}^{\frac{n}{2}-1} Z_{2j} Z_{2j+1}. \end{aligned}$$

Then, we can generate

$$\begin{aligned} \begin{aligned} H_{(2)}&= H_{12} + H_{n-1,n}\\&= \gamma _{AB}(Z_1 Z_2 + Z_{n-1} Z_{n}) + 4\gamma _{AB}\sum _{j=1}^{\frac{n}{2}-2}Z_{2j+1}Z_{2j+2} + 4\gamma _{BA} \sum _{j=1}^{\frac{n}{2}-1} Z_{2j}Z_{2j+1}. \end{aligned} \end{aligned}$$

(48)

Now we generate

$$\begin{aligned} \begin{aligned} \gamma _{AB} H_{(2)} - 4\gamma _{BA}H_{Z2}&= (\gamma _{AB}^2 - 4\gamma _{BA}^2)(Z_1 Z_2 + Z_{n-1} Z_n)\\&\quad + (4\gamma _{AB}^2 - 4\gamma _{BA}^2) \sum _{j=1}^{\frac{n}{2}-2} Z_{2j+1} Z_{2j+2}\\&= (\gamma _{AB}^2 - 4\gamma _{BA}^2)\sum _{j=0}^{\frac{n}{2}-1} Z_{2j+1}Z_{2j+2} + 3 \gamma _{AB}^2 \sum _{j=1}^{\frac{n}{2}-2} Z_{2j+1}Z_{2j+2}. \end{aligned} \end{aligned}$$

(49)

Define $\gamma = (\gamma _{AB}^2 - 4\gamma _{BA}^2)$ and

$$\begin{aligned} H_{(3)}= & {} \sum _{j=0}^{\frac{n}{2}-1} Z_{2j+1}Z_{2j+2} + 3 \frac{\gamma _{AB}^2}{\gamma } \sum _{j=1}^{\frac{n}{2}-2} Z_{2j+1}Z_{2j+2}, \end{aligned}$$

(50)

$$\begin{aligned} H_{Z2} -\gamma _{AB}H_{(3)}= & {} \gamma _{AB} \sum _{j=1}^{\frac{n}{2}-1} Z_{2j} Z_{2j+1} - 3 \frac{\gamma _{AB}^2}{\gamma } \gamma _{BA} \sum _{j=1}^{\frac{n}{2}-2} Z_{2j+1}Z_{2j+2}. \end{aligned}$$

(51)

Define $\tilde{\gamma }_2 = 3 \frac{\gamma _{AB}}{\gamma } \gamma _{BA}$ and

$$\begin{aligned} H_{*} = \sum _{j=1}^{\frac{n}{2}-1} Z_{2j} Z_{2j+1} - \tilde{\gamma }_2 \sum _{j=1}^{\frac{n}{2}-2} Z_{2j+1}Z_{2j+2}. \end{aligned}$$

On the other hand, consider

$$\begin{aligned} \begin{aligned} H_{(2)}-\gamma _{AB}H_{(3)} = 4\gamma _{BA} \sum _{j=1}^{\frac{n}{2}-1} Z_{2j} Z_{2j+1} + (3\gamma _{AB} - 3\frac{\gamma _{AB}^3}{\gamma }) \sum _{j=1}^{\frac{n}{2}-2} Z_{2j+1}Z_{2j+2}. \end{aligned} \end{aligned}$$

(52)

And define $\tilde{\gamma }_1 = 3\gamma _{AB}(1-\frac{\gamma _{AB}^2}{\gamma })\frac{1}{4\gamma _{BA}},$

$$\begin{aligned} H_{\Box } = \sum _{j=1}^{\frac{n}{2}-1} Z_{2j}Z_{2j+1} + \tilde{\gamma }_1 \sum _{j=1}^{\frac{n}{2}-2} Z_{2j+1}Z_{2j+2}. \end{aligned}$$

Then

$$\begin{aligned} \begin{aligned} H_{\circ } = H_{\Box } - H_{*} = (\tilde{\gamma }_1 - \tilde{\gamma }_2) \sum _{j=1}^{\frac{n}{2}-1} Z_{2j+1}Z_{2j+2}. \end{aligned} \end{aligned}$$

(53)

Finally,

$$\begin{aligned} \begin{aligned} H_{\Box } - \frac{\tilde{\gamma }_1}{(\tilde{\gamma }_1 - \tilde{\gamma }_2)}H_{\circ } = \sum _{j=1}^{\frac{n}{2}-1} Z_{2j}Z_{2j+1} = \frac{1}{\gamma _{AB}} H_{AB}. \end{aligned} \end{aligned}$$

(54)

Note that we have $\gamma \ne 0$, $\tilde{\gamma }_1 \ne 0$, $\tilde{\gamma }_2 \ne 0$, $\tilde{\gamma }_1 \ne \tilde{\gamma }_2$ and since $\gamma \ne 0$, $\gamma _{AB}^2 \ne 0$, $\gamma _{BA}^2 \ne 0$, we can generate $H_{AB}$ and $H_{BA}$ which gives the result. $\square$

Lemma 2Assume n is odd, then $iX_j \in \langle iH_A, iH_B, iH_{AB}, iH_{BA}, iH_X \rangle _\mathrm{Lie}$for any $j \in \{1, \ldots , n\}$.

Proof

Let us first see that $iX_1 \in \mathcal {L}$. Consider

$$\begin{aligned} \begin{aligned} {[}H_{AB}, H_X]&= (2i) \sum _{j=1}^{\frac{n}{2} -1 | \frac{n-1}{2}} Z_{2j} Y_{2j+1} + Y_{2j} Z_{2j+1}. \end{aligned} \end{aligned}$$

(55)

Define $H_{YZ|AB} = \sum _{j=1}^{\frac{n}{2} -1 | \frac{n-1}{2}} Z_{2j} Y_{2j+1} + Y_{2j} Z_{2j+1}$ and consider

$$\begin{aligned} \begin{aligned} {[}H_{YZ|AB}, H_{AB}]&= (2i)\sum _{j=1}^{\frac{n}{2} -1 | \frac{n-1}{2}} X_{2j+1} + (2i) \sum _{j=1}^{\frac{n}{2} | \frac{n-1}{2}} X_{2j}. \end{aligned} \end{aligned}$$

(56)

Notice that in the last sum, all X Pauli matrices appear, except the one acting on qubit 1. Thus,

$$\begin{aligned} H_X - \sum _{j=1}^{\frac{n}{2} -1 | \frac{n-1}{2}} X_{2j+1} + X_{2j} = X_1. \end{aligned}$$

And we have that $X_1 \in \mathcal {L}$. Assume now that we want to generate $X_{k}$ and that we have generated $X_{k-1}$. If k is even, then

$$\begin{aligned} {[}H_{BA}, X_{k-1}]= & {} (2i)Y_{k-1}Z_k, \end{aligned}$$

(57)

$$\begin{aligned} {[}Y_{k-1}Z_k, X_{k-1}]= & {} (-2i) Z_{k-1}Z_k. \end{aligned}$$

(58)

And finally,

$$\begin{aligned} {[}H_{XA}, Z_{k-1}Z_k]= & {} \sum _{j=1}^{\frac{n}{2} -1 | \frac{n-1}{2}} [X_{2j}, Z_{k-1}Z_k] = (-2i) Z_{k-1}Y_{k}, \end{aligned}$$

(59)

$$\begin{aligned} {[}H_{BA}, Z_{k-1}Y_{k}]= & {} \left[ \sum _{j=0}^{\frac{n}{2} -1 | \frac{n-3}{2}} Z_{2j+1} Z_{2j+2}, Z_{k-1}Y_{k} \right] = (-2i) X_k. \end{aligned}$$

(60)

Now if k is odd,

$$\begin{aligned} {[}H_{AB}, X_{k-1}]= & {} \sum _{j=1}^{\frac{n}{2} -1 | \frac{n-1}{2}} [Z_{2j}Z_{2j+1}, X_{k-1}]\nonumber \\= & {} (2i)Y_{k-1}Z_k, \end{aligned}$$

(61)

$$\begin{aligned} {[}Y_{k-1}Z_k, X_{k-1}]= & {} (-2i) Z_{k-1}Z_k, \end{aligned}$$

(62)

$$\begin{aligned} {[}H_{XB}, Z_{k-1}Z_k]= & {} (-2i) Z_{k-1}Y_{k}, \end{aligned}$$

(63)

$$\begin{aligned} {[}H_{AB}, Z_{k-1}Y_k]= & {} (-2i) X_k. \end{aligned}$$

(64)

It proves the result. $\square$

Proofs of results in Sect. 4

The following proposition shows that commuting terms in a Hamiltonian can be separated.

Proposition 4

Let $H_{Z1} = \omega _A H_A + \omega _B H_B$ and $H_{Z2} = \gamma _{AB} H_{AB} + \gamma _{BA} H_{BA}$ as defined above. Then, given that we can perform unitaries of the form $U_1 = e^{-iH_{Z1}t}$, then it is possible to apply unitaries of the form $U_{A}= e^{-iH_{A}t}$ and $U_{B}= e^{-iH_{B}t}$ if $\omega _A$ and $\omega _B$ are rationally independent. An analogous result holds for $H_{AB}$

Proof

Consider $t=\frac{2\pi }{\gamma _{A}}$ and notice that

$$\begin{aligned} U_1 = e^{-iH_{Z1}t}=e^{-i( \omega _A H_A + \omega _B H_B)t}= e^{-i2\pi H_{A}} e^{-i\frac{2\pi \omega _B}{\omega _A}H_{B}} = e^{-i\frac{2\pi \omega _B}{\omega _A}H_{B}}. \end{aligned}$$

Since $\omega _A$ and $\omega _B$ are rationally independent, we can generate the unitary $U_B$, and by the same argument, we can generate $U_A$. Same proof applies to $H_{Z2}$. $\square$

Proof for universality on square Grid

Here, we include the proofs for Sect. 4.2.

Theorem 4 Given a graph G as described above, vertices numbered in the order mentioned previously, and given the Hamiltonians $H_{A1}$, $Z_{N+1}$, $Z_{N+2}$, $X_{N+1}$, $X_{N+2}$, $X_{Grid}$, $H_{A2}$, $Z_{1} Z_{N+1}$, $Z_{n} Z_{N+2}$, then for $i\in \{1,\ldots ,n-1\}$and $j\in \{1,\ldots ,n\}$we have that $Z_j$, $X_j$ ,$Z_i Z_{i+1} \in \langle H_{A1}$, $Z_{N+1}$, $Z_{N+1}$, $H_{A2}$, $Z_{1} Z_{N+1}$, $Z_{n} Z_{N+2}\rangle _\mathrm{Lie}$. This implies universality for any n on the grid.

Proof

To show this, we can apply commutators over the available operators and obtain the two body terms and one body terms required. This can be done in a purely algebraic way, but it is also useful to relate these algebraic operations to operations over the graph. First, the algebraic proof is given, and then, we will relate it to operations over the graph.

Let us begin with the fact that $[Z_{1} Z_{N+1}, X_{Grid}] = Y_{1} Z_{N+1}$ (up to global phase). Also $[Y_{1} Z_{N+1}, Z_{1} Z_{N+1}] = X_1$ and thus we can also generate $Z_1$.

Now note

$$\begin{aligned} {[}Y_{1} Z_{N+1}, H_{A2}] = Z_{N+1}X_{1}Z_{n+1} + Z_{N+1}X_{1}Z_{2}. \end{aligned}$$

(65)

Then, since we can generate $Y_1$, we can also generate $Z_{N+1}Z_{1}Z_{n+1} + Z_{N+1}Z_{1}Z_{2}$. Thus we have $[Z_{N+1}Y_{1} , Z_{N+1}Z_{1}Z_{n+1} + Z_{N+1}Z_{1}Z_{2}]= X_{1}Z_{n+1} + X_{1}Z_{2}$ And then we can generate $Z_{1}Z_{n+1} + Z_{1}Z_{2}$.

Note that we have now generated a Hamiltonian $H^{(2)} = Z_{1}Z_{n+1} + Z_{1}Z_{2}$ that corresponds to edges (1, 2) and (1, 6).

We will use a similar procedure to prepare Hamiltonians of the form $H^{(k)}=Z_{k-1}Z_k + R^{(k)}$, where $R^{(k)}$ does not contain the operator $Z_k$. In this way, when we generate $H^{(n)}$, we will commute it with $Z_{n} Z_{N+2}$ in order to generate $Z_{k-1}Z_k$; starting from this, we will be able to generate all two body terms for the first line of the form $Z_j Z_{j+1}$.

We proceed by induction; assume that we have a Hamiltonian

$$\begin{aligned} H^{(k)}=Z_{k-1}Z_k + R^{(k)}, \end{aligned}$$

(66)

where $R^{(k)}$ does not have any terms with operators $Z_k$, nor neighbours $Z_{n+k}$ and $Z_{k+1}$ and also in any vertex on the line from k to n (same for Y and X operators). Actually, it does not contain operators from the kth column to the nth.

Note that we assume that there is a vertex numbered $k+1$. We also assume we have an operator

$$\begin{aligned} H^{(k)}_{A1} = X_k + X_{k+1} + \ldots + X_{n} + X_{R}^{(k)}, \end{aligned}$$

(67)

where $X_{R}^{(k)}$ is an operator without terms containing operators with support in the neighbours of vertex k and also in any vertex on the line from k to n, as before, we assume also that it does not contain operators from the kth column to the nth. Note that

$$\begin{aligned} \begin{aligned} {[}H^{(k)}, H^{(2)}_{A1}]&= [Z_{k-1}Z_k + R^{(k)}, X_k + X_{k+1} + \cdots + X_{n} + X_{R}^{(k)}]\\&= Z_{k-1} Y_k + [R^{(k)}, X_{R}^{(k)}], \end{aligned} \end{aligned}$$

(68)

where now $[R^{(k)}, X_{R}^{(k)}]$ does not contain operators from the kth column to the nth. Note that $Z_{k-1}$ was not affected by the operation since $X_{R}^{(k)}$ does not have support over vertex k-1. Perform now the operation

$$\begin{aligned} \begin{aligned} {[}[H^{(k)}, H^{(k)}_{A1}], H^{(k)}]&=[Z_{k-1} Y_k + [R^{(k)}, X_{R}^{(k)}], Z_{k-1}Z_k + R^{(k)}]\\&= X_k + [[R^{(k)}, X_{R}^{(k)}], R^{(k)}], \end{aligned} \end{aligned}$$

(69)

where $[[R^{(k)}, X_{R}^{(k)}], R^{(k)}]$ has no support from column k to column n. Define

$$\begin{aligned} \begin{aligned} H_{A1}^{(k+1)}&= H_{A1}^{(k)} - X_k - [[R^{(k)}, X_{R}^{(k)}], R^{(k)}]\\&= X_k + X_{k+1} + \cdots + X_{n} + X_{R}^{(k)} - X_k - [[R^{(k)}, X_{R}^{(2)}]\\&= X_{k+1} + \cdots + X_{n} + X_{R}^{(k+1)}, \end{aligned} \end{aligned}$$

(70)

where now $X_{R}^{(k+1)}$ does not have support on $k+1$ or neighbours or from column $k+1$ to n.

Assume as well there is an operator $H^{(k)}_{A2}$. This operator has terms $Z_{k}Z_{neigh(k)}$ (except $Z_{k-1} Z_k$); any other term does not have support in k or its neighbours.

Notice now that

$$\begin{aligned} \begin{aligned} {[}[H^{(k)}, H^{(k)}_{A1}], H^{(k)}_{A2}]&= [Z_{k-1} Y_k + [R^{(k)}, X_{R}^{(2)}], H^{(k)}_{A2} ] \\&= Z_{k-1} X_k Z_{k+1} + Z_{k-1} X_k Z_{k+n} + [[R^{(2)}, X_{R}^{(2)}],H^{(k)}_{A2} ], \end{aligned} \end{aligned}$$

(71)

where $[[R^{(2)}, X_{R}^{(2)}],H^{(k)}_{A2} ]$ has no support on k, $k+1$ or from columns $k+1$ to n.

Now consider the commutator

$$\begin{aligned} \begin{aligned}&{[}[H^{(k)}, H^{(2)}_{A1}], Z_{k-1} X_k Z_{k+1} + Z_{k-1} X_k Z_{k+n} + [[R^{(2)}, X_{R}^{(2)}],H^{(k)}_{A2} ] ] \\&\quad = [Z_{k-1} Y_k + [R^{(2)}, X_{R}^{(2)}], Z_{k-1} X_k Z_{k+1} + Z_{k-1} X_k Z_{k+n} + [[R^{(2)}, X_{R}^{(2)}],H^{(k)}_{A2} ] ]]\\&\quad = Z_k Z_{k+1} + Z_k Z_{k+n} + \overline{R}^{(k+1)}\\&\quad = Z_k Z_{k+1} + R^{(k+1)} \\&\quad = H^{(k+1)}, \end{aligned} \end{aligned}$$

(72)

where $\overline{R}^{(k+1)}$ and $R^{(k+1)}$ have no support from column $k+1$ to n.

Finally, define $H_{A2}^{(k+1)} = H_{A2}^{(k)} - H^{(k+1)}$, and we have all the Hamiltonians necessary for step $k+1$ with the necessary properties.

We can continue this procedure until generating Hamiltonian $H^{(n)} = Z_{n-1}Z_n + R^{(n)}$. Recall that $R^{(n)}$ has no support on column n of the grid.

Now note that

$$\begin{aligned}{}[Z_n Z_{N+2}, X_{Grid}] = Y_n Z_{N+2}. \end{aligned}$$

(73)

And we can thus generate $X_n$. Commuting this with $H^{(n)}$ gives $Z_{n-1}X_n Z_{N+2}$ and commuting again with $Y_n Z_{N+2}$, we obtain $Z_{n-1}Z_{n}$. We can now repeat this process with $H_{n-1}$ and $Z_{n-1}Z_{n}$. In this way, we can generate all the single Pauli operators on the line ${1,\ldots ,n}$ and also the two body operators of the form $Z_{k}Z_{k+1}$ on the line. $\square$