Modeling the plankton–fish dynamics with top predator interference and multiple gestation delays

Abstract

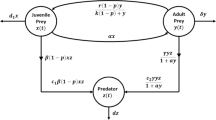
Many prey organisms have developed defense mechanisms against predation. If the predator can encounter in a limited spatial domain, the feeding rates reflect interference between predators and the corresponding functional response depends on both predator and prey densities. In this manuscript, an attempt has been made to understand the role of top predator interference and gestation delays on the dynamics of a three-species food chain model involving intermediate and top predators population. Interaction between the prey and an intermediate predator follows the Monod–Haldane functional response, while that between the top predator and its prey depends on Beddington–DeAngelis-type functional response. Analytically, we study the essential mathematical features such as boundedness, stability and direction of bifurcating periodic solution around the coexisting equilibrium for the model system. Numerically, we study the Hopf and transcritical bifurcations scenarios with respect to inhibitory effect of phytoplankton against zooplankton and death rate of fish population for the non-delayed system. Further, we study the stability behavior of the delayed model system. Model system exhibits irregular behavior when the interference is high or gestation period is larger than its critical value. Further, the system shows extinction of predators with the increase in inhibitory effect. Stability domain plots with respect to different important system parameters for non-delayed system and delay parameters for delayed system give a significant impact to study the stability of the different equilibrium points and bifurcation scenarios of both non-delayed and delayed systems. Our results point out the complexity of three-way interactions between phytoplankton, zooplankton and fish population in marine environment and highlight the role of predator interference and gestation delays in exhibiting the chaotic dynamics and extinction of predator population.

Appendix

In order to compute the properties of the Hopf bifurcation, we denote any one of the critical values of $\tau$ by $\tau ^*$ without generality loss, and a pair of purely imaginary roots $\pm i \omega _0$ exists in Eq. (3.13) by which system undergoes Hopf bifurcation. Let $N=N^*+x_1$, $P=P^*+x_2$, $Z=Z^*+x_3$, $\mu =\tau -\tau ^*$, where $\mu \in \mathrm{Re}$. Rescaling the time by $t \longrightarrow \frac{t}{\tau }$, system (3.1) can be written into the following continuous real-valued functions as $C=([-1,0],\mathrm{Re}^3)$

$$\begin{aligned} \dot{x}(t)=L_\mu (x_t)+f(\mu ,x_t), \end{aligned}$$

(7.1)

where $x(t)=(x_1(t),x_2(t),x_3(t))^T\in \mathrm{Re}^3$ and $L_\mu :C\rightarrow \mathrm{Re}^3, \ f:\mathrm{Re}\times C\rightarrow \mathrm{Re}^3$ are given, respectively,

$$\begin{aligned} L_\mu (\phi )=(\tau ^*+\mu )[J_1 \phi (0)+J_2 \phi (-1)], \end{aligned}$$

(7.2)

such that

$$\begin{aligned} J_1= & {} \left( \begin{array}{ccc} -\frac{rN^*}{K}+\frac{2jw_1N^{*2}P^*}{(jN^{*2}+a)^2} &{}\quad -\frac{w_1N^*}{(jN^{*2}+a)} &{}\quad 0 \\ 0 &{}\quad \frac{w_3P^*Z^*}{(P^*+bZ^*+c)^2} &{}\quad -\frac{(P^*+c)w_3P^*}{(P^*+bZ^*+c)^2} \\ 0 &{}\quad 0 &{}\quad 0 \end{array}\right) ,\\ J_2= & {} \left( \begin{array}{ccc} 0 &{}\quad 0 &{}\quad 0 \\ \\ -\frac{w_2P^*(jN^{*2}-a)}{(jN^{*2}+a)^2} &{}\quad 0 &{}\quad 0 \\ \\ 0 &{}\quad \frac{(bZ^*+c)w_4Z^*}{(P^*+bZ^*+c)^2} &{}\quad -\frac{w_4bP^*Z^*}{(P^*+bZ^*+c)^2} \end{array}\right) , \end{aligned}$$

and

$$\begin{aligned} f(\mu ,\phi )=(\tau ^*+\mu )\left( \begin{array}{c} -\frac{r}{K}\phi _{1}^{2}(0) - \frac{w_1\phi _1(0) \phi _2(0)}{j\phi _{1}^{2}(0)+a} \\ \frac{w_2\phi _1(-1)\phi _2(0)}{j\phi _{1}^{2}(-1)+a}-\frac{w_3\phi _2(0)\phi _3(0)}{\phi _2(0)+b\phi _3(0)+c} \\ \frac{w_4\phi _2(-1)\phi _3(0)}{\phi _2(-1)+b\phi _3(-1)+c} \end{array}\right) ,\nonumber \\ \end{aligned}$$

(7.3)

where $\phi (\theta )=(\phi _1(\theta ),\phi _2(\theta ),\phi _3(\theta ))^T \in C([-1,0],\mathrm{Re}^3)$.

By the Riesz representation theorem, there exist a function $\eta (\theta ,\mu )$ of bounded variation for $\theta \in [-1,0]$, such that

$$\begin{aligned} L_\mu \phi = \int _{-1}^{0} \mathrm{d}\eta (\theta ,\mu )\phi (\theta ), \quad \text {for} \quad \phi \in C. \end{aligned}$$

(7.4)

In fact, we can take

$$\begin{aligned} \eta (\theta ,\mu )=(\tau ^*+\mu )[J_1 \delta (\theta )+J_2 \delta (\theta +1)], \end{aligned}$$

(7.5)

where $\delta (\theta )$ is the Dirac delta function.

For $\phi \in C_1 ([-1,0],\mathrm{Re}^3)$, define

$$\begin{aligned} A(\mu )\phi = {\left\{ \begin{array}{ll} \frac{\mathrm{d}\phi (\theta )}{\mathrm{d}\theta }, &{} \theta \in [-1,0),\\ \int _{-1}^{0} \phi (s) \mathrm{d}\eta (s,\mu ), &{} \theta =0 \end{array}\right. } \end{aligned}$$

(7.6)

and

$$\begin{aligned} R(\mu )\phi = {\left\{ \begin{array}{ll} 0, &{} \theta \in [-1,0),\\ f(\mu ,\phi ), &{} \theta =0. \end{array}\right. } \end{aligned}$$

(7.7)

System (7.1) is then equivalent to

$$\begin{aligned} \dot{x_t}=A(\mu ) x_t +R(\mu ) x_t, \end{aligned}$$

(7.8)

where $x_t(\theta )=x(t+\theta )$ for $\theta \in [-1,0].$

For $\psi \in C^1([0,1],(\mathrm{Re}^3)^*)$, define

$$\begin{aligned} A^* \psi (s)= {\left\{ \begin{array}{ll} -\frac{\mathrm{d}\psi (s)}{\mathrm{d}s} &{} s\in (0,1],\\ \int _{-1}^0 \psi (-t)\mathrm{d}\eta ^T (t,0), &{} s = 0, \end{array}\right. } \end{aligned}$$

(7.9)

and a bilinear inner product is given by

$$\begin{aligned} \begin{aligned} \langle \psi (s), \phi (\theta ) \rangle&=\overline{\psi }(0)\phi (0)-\int _{\theta =-1}^0 \int _{\xi =0}^\theta \overline{\psi }(\xi -\theta )\\&\quad \times \mathrm{d}\eta (\theta )\phi (\xi )\mathrm{d}\xi , \end{aligned} \end{aligned}$$

(7.10)

where $\overline{\psi }(0)$ and $\overline{\psi }(\xi -\theta )$ are the complex conjugate of $\psi (0)$ and $\psi (\xi -\theta )$.

For further calculation, we assume that $i\omega _0\tau ^*$ and $-i\omega _0\tau ^*$ are eigenvalues of A(0) and $A^*$, respectively.

Now, let $q(\theta )=(1,\sigma _2,\sigma _3)^T \mathrm{e}^{i\omega _0\tau ^*\theta }$ and $q^*(s)=M (1,\sigma _2^*,\sigma _3^*)$$\times \mathrm{e}^{i\omega _0\tau ^* s}$ are the eigenvector of A(0) and $A^*(0)$ corresponding to $+i\omega _0\tau ^*$ and $-i\omega _0\tau ^*$, respectively. Then,

$$\begin{aligned} Aq(\theta )=i\omega _0\tau ^*q(\theta ), \end{aligned}$$

(7.11)

and for $\theta =0$, we obtained

$$\begin{aligned} \tau ^*\left( \begin{array}{ccc} i\omega _0+\frac{rN^*}{K}-\frac{2jw_1N^{*2}P^*}{(jN^{*2}+a)^2} &{}\quad \frac{w_1N^*}{(jN^{*2}+a)}&{}\quad 0 \\ \mathrm{e}^{-i\omega _0\tau ^*}\frac{w_2P^*(jN^{*2}-a)}{(jN^{*2}+a)^2} &{}\quad \quad i\omega _0-\frac{w_3P^*Z^*}{(P^*+bZ^*+c)^2} &{}\quad \frac{(P^*+c)w_3P^*}{(P^*+bZ^*+c)^2} \\ 0 &{}\quad -\mathrm{e}^{-i\omega _0\tau ^*}\frac{(bZ^*+c)w_4Z^*}{(P^*+bZ^*+c)^2} &{}\quad i\omega _0+\mathrm{e}^{-i\omega _0\tau ^*}\frac{w_4bP^*Z^*}{(P^*+bZ^*+c)^2} \end{array}\right) q(0)=\left( \begin{array}{ccc} 0 \\ \\ 0 \\ \\ 0 \end{array}\right) . \end{aligned}$$

(7.12)

Solving the system of equations, we get

$$\begin{aligned} \sigma _2&=\frac{2jN^*P^*}{(jN^{*2}+a)}-\frac{r(jN^{*2}+a)}{w_1K}-\frac{i\omega _0(jN^{*2}+a)}{w_1N^*}, \end{aligned}$$

and

$$\begin{aligned} \sigma _3=\frac{\sigma _2w_4Z^*(bZ^*+c)}{\mathrm{e}^{i\omega _0\tau ^*}i\omega _0(P^*+bZ^*+c)^2+w_4bP^*Z^*}. \end{aligned}$$

Similarly, let

$$\begin{aligned} A^*q^*(s)=-i\omega _0\tau ^*q^*(s), \end{aligned}$$

(7.13)

where

$$\begin{aligned} \sigma _{2}^{*}&=\frac{2jw_1N^{*2}}{\mathrm{e}^{-i\omega _0\tau ^*}w_2(jN^*-a)}-\frac{rN^*(jN^{*2}+a)^2}{\mathrm{e}^{-i\omega _0\tau ^*}w_2KP^*(jN^*-a)}\\&\quad -\frac{i\omega _0(jN^{*2}+a)^2}{\mathrm{e}^{-i\omega _0\tau ^*}w_2P^*(jN^*-a)}, \end{aligned}$$

and

$$\begin{aligned} \sigma _{3}^{*}=-\frac{\sigma _2^*w_3P^*(P^*+c)}{\mathrm{e}^{-i\omega _0\tau ^*}w_4bP^*Z^*+i\omega _0(P^*+bZ^*+c)^2}. \end{aligned}$$

Under the normalization condition $\langle q^*(s),q(\theta ) \rangle = 1$, we have

$$\begin{aligned} M=\frac{1}{\overline{D}}, \end{aligned}$$

where

$$\begin{aligned} D&=1+ \sigma _2\overline{\sigma }_2^*+ \sigma _3\overline{\sigma }_3^*+ \tau ^*\Bigg (-\frac{\overline{\sigma }_2^*w_2P^*(jN^{*2}-a)}{(jN^{*2}+a)^2}\\&\quad +\frac{\overline{\sigma }_3^*w_4Z^*\big (\sigma _2(bZ^*+c)- \sigma _3bP^*\big )}{(P^*+bZ^*+c)^2}\Bigg )\mathrm{e}^{-i\omega _0\tau ^*} \end{aligned}$$

and $\overline{D}$ is the complex conjugate of D.

Now following in the same manner as given in [61], we obtained

$$\begin{aligned} g(z,\bar{z})&=\tau ^* \overline{M} (1,\overline{\sigma }_2^*, \overline{\sigma }_3^*) \left( \begin{array}{c} -\frac{r}{K}\phi _{1}^{2}(0) - \frac{w_1\phi _1(0) \phi _2(0)}{j\phi _{1}^{2}(0)+a}\\ \frac{w_2\phi _1(-1)\phi _2(0)}{j\phi _{1}^{2}(-1)+a}-\frac{w_3\phi _2(0)\phi _3(0)}{\phi _2(0)+b\phi _3(0)+c} \\ \frac{w_4\phi _2(-1)\phi _3(0)}{\phi _2(-1)+b\phi _3(-1)+c} \end{array}\right) , \end{aligned}$$

(7.14)

which can also be written as

$$\begin{aligned} g(z,\bar{z})&=\tau ^* \overline{M} (1,\overline{\sigma }_2^*, \overline{\sigma }_3^*) \left( \begin{array}{c} -\frac{r}{K}x_{1t}^{2}(0) - \frac{w_1x_{1t}(0) x_{2t}(0)}{jx_{1t}^{2}(0)+a} \\ \frac{w_2x_{1t}(-1)x_{2t}(0)}{jx_{1t}^{2}(-1)+a}-\frac{w_3x_{2t}(0)x_{3t}(0)}{x_{2t}(0)+bx_{3t}(0)+c} \\ \frac{w_4x_{2t}(-1)x_{3t}(0)}{x_{2t}(-1)+bx_{3t}(-1)+c} \end{array}\right) ,\nonumber \\ \end{aligned}$$

(7.15)

where

$$\begin{aligned} x_{1t}(0)&= z+ \overline{z} + W_{20}^{(1)} (0) \frac{z^2}{2} + W_{11}^{(1)} (0) z \overline{z}\\&\quad +W_{02}^{(1)} (0) \frac{\overline{z}^2}{2} +\cdots ,\\ x_{2t}(0)&= \sigma _2 z+ \overline{\sigma }_2 \overline{z} + W_{20}^{(2)} (0) \frac{z^2}{2} + W_{11}^{(2)} (0) z \overline{z}\\&\quad + W_{02}^{(2)} (0) \frac{\overline{z}^2}{2} +\cdots ,\\ x_{3t}(0)&=\sigma _3z+\overline{\sigma }_3\overline{z}+W_{20}^{(3)}(0)\frac{z^2}{2}+W_{11}^{(3)}(0)z\overline{z}\\&\quad +W_{02}^{(3)}(0)\frac{\overline{z}^2}{2}+\cdots ,\\ x_{1t}(-1)&= z \mathrm{e}^{-i\omega _0 \tau ^*} + \overline{z} \mathrm{e}^{i\omega _0 \tau ^*} + W_{20}^{(1)} (-1) \frac{z^2}{2}\\&\quad + W_{11}^{(1)} (-1) z \overline{z} + W_{02}^{(1)} (-1) \frac{\overline{z}^2}{2} +\cdots ,\\ x_{2t}(-1)&=\sigma _2z \mathrm{e}^{-i\omega _0 \tau ^*} + \overline{\sigma }_2\overline{z} \mathrm{e}^{i\omega _0 \tau ^*} + W_{20}^{(2)} (-1) \frac{z^2}{2}\\&\quad + W_{11}^{(2)} (-1) z \overline{z} + W_{02}^{(2)} (-1) \frac{\overline{z}^2}{2} +\cdots ,\\ x_{3t}(-1)&=\sigma _3z \mathrm{e}^{-i\omega _0 \tau ^*} + \overline{\sigma }_3\overline{z} \mathrm{e}^{i\omega _0 \tau ^*} + W_{20}^{(3)} (-1) \frac{z^2}{2}\\&\quad + W_{11}^{(3)} (-1) z \overline{z} + W_{02}^{(3)} (-1) \frac{\overline{z}^2}{2} +\cdots . \end{aligned}$$

From Eq. (7.15), we obtained the value of $g_{20}$, $g_{11}$, $g_{02}$ and $g_{21}$ which is given in Sect. 4.

To compute $g_{21}$, we have to compute the values of $W_{20}^{(l)}(\theta )$ and $W_{11}^{(l)}(\theta )$, for $l=1,2,3.$

Now, we denote $W_{20}(\theta ) {=} (W_{20}^{(1)}(\theta ){,}W_{20}^{(2)}(\theta ){,}W_{20}^{(3)}(\theta ))^T$ and $W_{11}(\theta ) {=} (W_{11}^{(1)}(\theta ),W_{11}^{(2)}(\theta ),W_{11}^{(3)}(\theta ))^T$.

By computing, we obtained

$$\begin{aligned} \begin{aligned} W_{20}(\theta )&=-\frac{g_{20}}{i\omega _0\tau ^*} q(\theta ) - \frac{\overline{g}_{02}}{3i\omega _0\tau ^*} \overline{q}(\theta )\\&\quad + E_1 \mathrm{e}^{2i\omega _0\tau ^*\theta }, \end{aligned} \end{aligned}$$

(7.16)

and

$$\begin{aligned} \begin{aligned} W_{11}(\theta )&=\frac{g_{11}}{i\omega _0\tau ^*} q(0) \mathrm{e}^{i\omega _0\tau ^*\theta }\\&\quad - \frac{\overline{g}_{11}}{i\omega _0\tau ^*} \overline{q}(0) \mathrm{e}^{-i\omega _0\tau ^*\theta } + E_2. \end{aligned} \end{aligned}$$

(7.17)

Here, $E_1 = (E_1^{(1)},E_1^{(2)},E_1^{(3)})$ and $E_2 = (E_2^{(1)},E_2^{(2)},E_2^{(3)}) \in \mathrm{Re}^3$ are the constant vectors, which we have to be determined.

Now using [61], we have

$$\begin{aligned} E_1= \frac{2}{M_1} \left( \begin{array}{c} -\frac{r}{K}-\frac{w_1\sigma _2}{a} \\ \frac{\sigma _2w_2\mathrm{e}^{-i\omega _0\tau ^*}}{a}-\frac{\sigma _2\sigma _3w_3}{c} \\ \frac{\sigma _2\sigma _3w_4\mathrm{e}^{-i\omega _0\tau ^*}}{c} \end{array}\right) . \end{aligned}$$

Solve this system for $E_1$, we obtained

$$\begin{aligned} E_{1}^{(1)}= & {} \frac{2}{M_1} \left| \begin{array}{ccc} -\frac{r}{K}-\frac{w_1\sigma _2}{a} &{}\quad \frac{w_1N^*}{(jN^{*2}+a)}&{}\quad 0 \\ \frac{\sigma _2w_2\mathrm{e}^{-i\omega _0\tau ^*}}{a}-\frac{\sigma _2\sigma _3w_3}{c} &{}\quad 2i\omega _0-\frac{w_3P^*Z^*}{(P^*+bZ^*+c)^2} &{}\quad \frac{(P^*+c)w_3P^*}{(P^*+bZ^*+c)^2}\\ \frac{\sigma _2\sigma _3w_4\mathrm{e}^{-i\omega _0\tau ^*}}{c} &{}\quad -\mathrm{e}^{-2i\omega _0\tau ^*}\frac{(bZ^*+c)w_4Z^*}{(P^*+bZ^*+c)^2} &{}\quad 2i\omega _0+\mathrm{e}^{-2i\omega _0\tau ^*}\frac{w_4bP^*Z^*}{(P^*+bZ^*+c)^2} \end{array}\right| ,\\ E_{1}^{(2)}= & {} \frac{2}{M_1} \left| \begin{array}{ccc} 2i\omega _0+\frac{rN^*}{K}-\frac{2jw_1N^{*2}P^*}{(jN^{*2}+a)^2} &{}\quad -\frac{r}{K}-\frac{w_1\sigma _2}{a} &{}\quad 0 \\ \mathrm{e}^{-2i\omega _0\tau ^*}\frac{w_2P^*(jN^{*2}-a)}{(jN^{*2}+a)^2} &{}\quad \frac{\sigma _2w_2\mathrm{e}^{-i\omega _0\tau ^*}}{a}-\frac{\sigma _2\sigma _3w_3}{c} &{}\quad \frac{(P^*+c)w_3P^*}{(P^*+bZ^*+c)^2} \\ 0 &{}\quad \frac{\sigma _2\sigma _3w_4\mathrm{e}^{-i\omega _0\tau ^*}}{c} &{}\quad 2i\omega _0+\mathrm{e}^{-2i\omega _0\tau ^*}\frac{w_4bP^*Z^*}{(P^*+bZ^*+c)^2} \end{array}\right| , \end{aligned}$$

and

$$\begin{aligned} E_{1}^{(3)}=\frac{2}{M_1} \left| \begin{array}{ccc} 2i\omega _0+\frac{rN^*}{K}-\frac{2jw_1N^{*2}P^*}{(jN^{*2}+a)^2} &{}\quad \frac{w_1N^*}{(jN^{*2}+a)} &{}\quad -\frac{r}{K}-\frac{w_1\sigma _2}{a} \\ \mathrm{e}^{-2i\omega _0\tau ^*}\frac{w_2P^*(jN^{*2}-a)}{(jN^{*2}+a)^2} &{}\quad 2i\omega _0-\frac{w_3P^*Z^*}{(P^*+bZ^*+c)^2} &{}\quad \frac{\sigma _2w_2\mathrm{e}^{-i\omega _0\tau ^*}}{a}-\frac{\sigma _2\sigma _3w_3}{c} \\ 0 &{}\quad -\mathrm{e}^{-2i\omega _0\tau ^*}\frac{(bZ^*+c)w_4Z^*}{(P^*+bZ^*+c)^2} &{}\quad \frac{\sigma _2\sigma _3w_4\mathrm{e}^{-i\omega _0\tau ^*}}{c} \end{array}\right| , \end{aligned}$$

where

$$\begin{aligned} M_1=\left( \begin{array}{ccc} 2i\omega _0+\frac{rN^*}{K}-\frac{2jw_1N^{*2}P^*}{(jN^{*2}+a)^2} &{}\quad \frac{w_1N^*}{(jN^{*2}+a)} &{}\quad 0 \\ \mathrm{e}^{-2i\omega _0\tau ^*}\frac{w_2P^*(jN^{*2}-a)}{(jN^{*2}+a)^2} &{}\quad 2i\omega _0-\frac{w_3P^*Z^*}{(P^*+bZ^*+c)^2} &{}\quad \frac{(P^*+c)w_3P^*}{(P^*+bZ^*+c)^2} \\ 0 &{}\quad -\mathrm{e}^{-2i\omega _0\tau ^*}\frac{(bZ^*+c)w_4Z^*}{(P^*+bZ^*+c)^2} &{}\quad 2i\omega _0+\mathrm{e}^{-2i\omega _0\tau ^*}\frac{w_4bP^*Z^*}{(P^*+bZ^*+c)^2} \end{array}\right) . \end{aligned}$$

Similarly, we have

$$\begin{aligned} E_2= \frac{2}{M_2} \left( \begin{array}{c} -\frac{r}{K} - \frac{w_1}{a}Re(\sigma _2) \\ \frac{w_2}{a}(\sigma _2\mathrm{e}^{i\omega _0\tau ^*}+\overline{\sigma }_2\mathrm{e}^{-i\omega _0\tau ^*}) -\frac{w_3}{c}Re(\sigma _2\overline{\sigma }_3) \\ \frac{w_4}{c}(\sigma _2\overline{\sigma }_3\mathrm{e}^{-i\omega _0\tau ^*}+\overline{\sigma }_2\sigma _3\mathrm{e}^{i\omega _0\tau ^*}) \end{array}\right) . \end{aligned}$$

Solve this system for $E_2$, we obtained

$$\begin{aligned} E_{2}^{(1)}= & {} \frac{2}{M_2} \left| \begin{array}{ccc} -\frac{r}{K}-\frac{w_1}{a}Re(\sigma _2) &{}\quad \frac{w_1N^*}{(jN^{*2}+a)} &{}\quad 0 \\ \frac{w_2}{a}(\sigma _2\mathrm{e}^{i\omega _0\tau ^*} +\overline{\sigma }_2\mathrm{e}^{-i\omega _0\tau ^*}) -\frac{w_3}{c}Re(\sigma _2\overline{\sigma }_3) &{}\quad -\frac{w_3P^*Z^*}{(P^*+bZ^*+c)^2} &{}\quad \frac{(P^*+c)w_3P^*}{(P^*+bZ^*+c)^2} \\ \frac{w_4}{c}(\sigma _2\overline{\sigma }_3\mathrm{e}^{-i\omega _0\tau ^*}+\overline{\sigma }_2\sigma _3\mathrm{e}^{i\omega _0\tau ^*}) &{}\quad -\frac{(bZ^*+c)w_4Z^*}{(P^*+bZ^*+c)^2} &{}\quad \frac{w_4bP^*Z^*}{(P^*+bZ^*+c)^2} \end{array}\right| ,\\ E_{2}^{(2)}= & {} \frac{2}{M_2} \left| \begin{array}{ccc} \frac{rN^*}{K}-\frac{2jw_1N^{*2}P^*}{(jN^{*2}+a)^2} &{}\quad -\frac{r}{K}-\frac{w_1}{a}Re(\sigma _2) &{}\quad 0 \\ \frac{w_2P^*(jN^{*2}-a)}{(jN^{*2}+a)^2} &{}\quad \frac{w_2}{a}(\sigma _2\mathrm{e}^{i\omega _0\tau ^*}+\overline{\sigma }_2\mathrm{e}^{-i\omega _0\tau ^*}) -\frac{w_3}{c}Re(\sigma _2\overline{\sigma }_3) &{} \frac{(P^*+c)w_3P^*}{(P^*+bZ^*+c)^2} \\ 0 &{} \frac{w_4}{c}(\sigma _2\overline{\sigma }_3\mathrm{e}^{-i\omega _0\tau ^*}+\overline{\sigma }_2\sigma _3\mathrm{e}^{i\omega _0\tau ^*}) &{} \frac{w_4bP^*Z^*}{(P^*+bZ^*+c)^2} \end{array}\right| , \end{aligned}$$

and

$$\begin{aligned} E_{2}^{(3)}=\frac{2}{M_2} \left| \begin{array}{ccc} \frac{rN^*}{K}-\frac{2jw_1N^{*2}P^*}{(jN^{*2}+a)^2} &{}\quad \frac{w_1N^*}{(jN^{*2}+a)} &{}\quad -\frac{r}{K}-\frac{w_1}{a}\mathrm{Re}(\sigma _2) \\ \frac{w_2P^*(jN^{*2}-a)}{(jN^{*2}+a)^2} &{}\quad -\frac{w_3P^*Z^*}{(P^*+bZ^*+c)^2} &{}\quad \frac{w_2}{a}(\sigma _2\mathrm{e}^{i\omega _0\tau ^*}+\overline{\sigma }_2\mathrm{e}^{-i\omega _0\tau ^*})-\frac{w_3}{c}\mathrm{Re}(\sigma _2\overline{\sigma }_3) \\ 0 &{}\quad -\frac{(bZ^*+c)w_4Z^*}{(P^*+bZ^*+c)^2} &{}\quad \frac{w_4}{c}(\sigma _2\overline{\sigma }_3\mathrm{e}^{-i\omega _0\tau ^*}+\overline{\sigma }_2\sigma _3\mathrm{e}^{i\omega _0\tau ^*}) \end{array}\right| , \end{aligned}$$

where

$$\begin{aligned} M_2=\left( \begin{array}{ccc} \frac{rN^*}{K}-\frac{2jw_1N^{*2}P^*}{(jN^{*2}+a)^2} &{}\quad \frac{w_1N^*}{(jN^{*2}+a)} &{}\quad 0 \\ \frac{w_2P^*(jN^{*2}-a)}{(jN^{*2}+a)^2} &{}\quad -\frac{w_3P^*Z^*}{(P^*+bZ^*+c)^2} &{} \frac{(P^*+c)w_3P^*}{(P^*+bZ^*+c)^2} \\ 0 &{}\quad -\frac{(bZ^*+c)w_4Z^*}{(P^*+bZ^*+c)^2} &{}\quad \frac{w_4bP^*Z^*}{(P^*+bZ^*+c)^2} \end{array}\right) . \end{aligned}$$

Consequently, we determine the value of $W_{20}(\theta )$ and $W_{11}(\theta )$ from Eqs. (7.16) and (7.17). The value of $g_{21}$ can be expressed by delay and parameters [Eq. (4.1)].