Resonance behavior of the system with a limited power supply having the Mises girder as absorber

Abstract

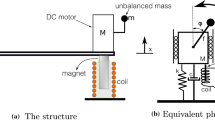
Three-DOF system with a limited power supply (or non-ideal system) having the Mises girder as absorber is considered. Stationary resonance regimes of vibrations near stable equilibrium positions of the system are constructed in two approximations of the multiple scales method. Namely, vibrations near the resonance 1:1 between the motor rotation frequency and the linear sub-system frequency and vibrations near the resonance 1:1 between the motor and absorber frequencies are analyzed. This analysis near the first resonance is made as in supposition that elastic springs of the Mises girder are weak and have an order of the small parameter, as well as in supposition that these springs are not weak. It is obtained that the effective absorption of the elastic vibrations can be obtained in the second case. Additional numerical simulation permits to find regimes of absorption when it is possible to guarantee also the fast outcome from the first resonance region. The most appropriate for absorption and such outcome from the first resonance are vibrations near the second resonance and the snap-through motions.

A Appendix

Let us look into initial equation for the motor motions, that is the third equation of system (4):

$$\begin{aligned} \ddot{\varphi } = \varepsilon \Big [ \rho \bigl ( u - \overline{r} \sin \varphi \bigr ) \cos \varphi + \overline{K} q - \bigl ( \overline{K} +h_1 \bigr ) \dot{\varphi } \Bigr ].\nonumber \\ \end{aligned}$$

(50)

After removing of all terms related to other parts of the system and substituting coefficients, it may be presented in the simplified form of some partial sub-system as:

$$\begin{aligned} \ddot{\varphi } + \varepsilon a \dot{\varphi } - \varepsilon b = 0. \end{aligned}$$

(51)

Exact solution of this equation is the following:

$$\begin{aligned} \dot{\varphi } = \dfrac{b}{a} (1 - C \mathrm{e}^{-\varepsilon at}). \end{aligned}$$

(52)

If we instead apply to Eq. (51) the multiple scales method, the following system is obtained:

$$\begin{aligned} D_0^2 \varphi _0= & {} 0 , \end{aligned}$$

(53)

$$\begin{aligned} D_0^2 \varphi _1= & {} -2D_0D_1\varphi _0 - aD_0\varphi _0 + b , \end{aligned}$$

(54)

$$\begin{aligned} D_0^2 \varphi _2= & {} -2D_0D_1\varphi _1- (D_1^2 + 2D_0D_2)\varphi _0 \nonumber \\&-\,a(D_0\varphi _1 + D_1\varphi _0) . \end{aligned}$$

(55)

Solution of the zeroth approximation Eq. (53) is taken in the form

$$\begin{aligned} \varphi _0 = pt_0 . \end{aligned}$$

(56)

To remove secular terms from Eq. (54), the following condition must be satisfied

$$\begin{aligned} 2p' + ap - b = 0. \end{aligned}$$

(57)

One has

$$\begin{aligned} p = \dfrac{b}{a} \left( 1 - C\mathrm{e}^{-\frac{1}{2} a t_1}\right) , \end{aligned}$$

(58)

where $C = C(t_2,\ldots )$.

Then we can obtain the following solution to $\varphi$ in the first approximation by the small parameter:

$$\begin{aligned} \dot{\varphi } = \dfrac{b}{a} \left( 1 - C \mathrm{e}^{-\frac{1}{2} \varepsilon at}\right) . \end{aligned}$$

(59)

Note that the exact solution (52) and the approximate solution (59) are similar, but the second one decreases two times slower that the first one. To obtain correct results using the multiple scales method, infinite amount of approximation steps must be taken. Then the p would take the following form

$$\begin{aligned} \dot{\varphi }= & {} \dfrac{b}{a} \Big (1 - C\mathrm{e}^{-\frac{1}{2} a t} \Big (-\dfrac{1}{2} \varepsilon at + \dfrac{1}{2 \cdot 2!} (\varepsilon at)^2 \nonumber \\&- \dfrac{1}{2 \cdot 3!}(\varepsilon at)^3 + \cdots \Big )\Big )\nonumber \\= & {} \dfrac{b}{a} (1 - C\mathrm{e}^{-\varepsilon a t_1}). \end{aligned}$$

(60)

The same result can be obtained by drop** coefficient 2 at $p'$ in Eq. (57). Returning to Eq. (19) in Sect. 3, it seems reasonable to make the same transformation in first equation of the system (19) without use of few additional approximation steps. Results of numerical simulation confirm an appropriateness of such correction.