Analytical solutions for resonant response of suspended cables subjected to external excitation

Abstract

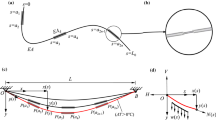
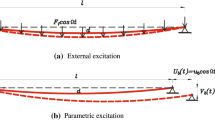
In this study, two analytical methods are applied to study the primary resonances response of suspended cables subjected to external excitation. We choose four different sag-to-span ratios and the first two modes to investigate the differences in nonlinear responses obtained with analytical methods. First, we summarize the equations of motion by applying the Hamilton’s principle and quasi-static assumption, and then these equations are discretized by the Galerkin procedure. Second, the multiple-scale method and homotopy analysis method are adopted to obtain the approximate solutions. Moreover, numerical integrations are introduced in order to verify the obtained approximate results. The numerical results show that frequency response curves obtained by different analytical methods show different quantitative predictions in some cases of motion, modes, and particular sag-to-span ratios. Finally, the differences in displacement fields and axial tension forces are compared and analyzed.

Appendix

$$\begin{aligned} \mathbf R _{nm}&= \frac{1}{(m-1)!}\frac{\partial ^{m-1} \mathcal {N}\left[ \varPhi _n(\tau ;q),A_n(q),\Delta _n(q),\varGamma _n(q)\right] }{\partial q^{m-1}}\Bigg |_{q=0}\\&= \varPi _1+\varPi _2+\varPi _3+\varPi _4\\ \varPi _1&= \varOmega _n^2\sum _{k=0}^{m-1}a_{nk}\ddot{u}_{nr}\\&+2\varOmega _n \mu _n \sum _{k=0}^{m-1}a_{nk} \dot{u}_{nr}\\&+\omega _n^2\left[ \left( \sum _{k=0}^{m-1}a_{nk}u_{r}\right) +\delta _{n,m-1}\right] ;\\ \varPi _2&= \varGamma _{nnn}\sum _{k=0}^{m-1}\delta _{nk}\delta _{nr}+2\varGamma _{nnn}\\&\sum _{k=0}^{m-1}\left( \sum _{p=0}^{k}a_{np}\delta _{n,k-p}\right) u_{r}\\&+\varGamma _{nnn}\left\{ \sum _{k=0}^{m-1}\left( \sum _{p=0}^{k}a_{np} a_{n,k-p}\right) \left( \sum _{p=0}^{r}u_{np} u_{n,r-p}\right) \right\} ;\\ \varPi _3&= \varLambda _{nnnn}\sum _{k=0}^{m-1}\left( \sum _{p=0}^{k}\delta _{np}\delta _{n,k-p}\right) \delta _{nr}\\&+\varLambda _{nnnn}\sum _{k=0}^{m-1}\left\{ \left[ \sum _{p=0}^{k}\left( \sum _{s=0}^{p}a_{ns} a_{n,p-s}\right) a_{n,k-p}\right] \right. \\&\left. \left[ \sum _{p=0}^{r}\left( \sum _{s=0}^{p}u_{ns} u_{n,p-s}\right) u_{n,r-p}\right] \right\} \\&+3\varLambda _{nnnn}\sum _{k=0}^{m-1}\left[ \sum _{p=0}^{k}\left( \sum _{s=0}^{p}a_{ns} a_{n,p-s}\right) \right. \\&\left. \left( \sum _{s=0}^{k-p}u_{ns} u_{n,k-p-s}\right) \delta _{nr}\right] \\&+3\varLambda _{nnnn}\sum _{k=0}^{m-1}\left( \sum _{p=0}^{k}a_{np} u_{n,k-p}\right) \left( \sum _{p=0}^{r}\delta _{p}\delta _{n,r-p}\right) ;\\ \varPi _4&= -\frac{f_n}{(m-1)!}\frac{\partial ^{m-1}\left[ \cos \tau \cos \varGamma _n(q) +\sin \tau \sin \varGamma _n(q) \right] }{\partial q^{m-1}}\Bigg |_{q=0}; \end{aligned}$$

in which $r=m-k-1$.