SpringerLink
Log in

A Stochastic Optimization Model to Reduce Expected Post-Disaster Response Time Through Pre-Disaster Investment Decisions

  • Published:
Networks and Spatial Economics Aims and scope Submit manuscript

Abstract

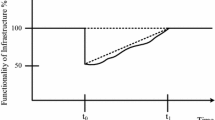
This paper seeks to enhance network survivability under a disaster and reduce the expected post-disaster response time for transportation networks through pre-disaster investment decisions. The planning focuses on determining the links of the network to strengthen through investment under two types of uncertainties: the disaster characteristics, and the surviving network under each disaster. A bi-level stochastic optimization model is proposed for this problem, in which link investment decisions are made at the upper level to enhance the network survivability subject to a budget constraint such that the expected post-disaster response time is minimized at the lower level. A two-stage heuristic algorithm is proposed to obtain effective solutions efficiently. The numerical experiments indicate that the proposed heuristic algorithm converges to a fixed point representing a feasible solution, within an acceptable tolerance level, of the bi-level stochastic optimization model which is an effective solution under disasters of moderate severity. Parametric and sensitivity analyses reinforce the need for a holistic approach that integrates multiple relevant considerations to determine the link investment decisions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price includes VAT (Germany)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  • Abdel-Rahim A, Oman P, Johnson B, Tung LW (2007) Survivability analysis of large-scale intelligent transportation system networks. Transp Res Rec J Transp Res Board 2022:9–20

    Article  Google Scholar 

  • Ball MO, Golden BL, Vohra RV (1989) Finding the most vital arcs in a network. Oper Res Lett 8(2):73–76

    Article  Google Scholar 

  • Bana e Costa CA, Oliveira CS, Vieira V (2008) Prioritization of bridges and tunnels in earthquake risk mitigation using multicriteria decision analysis: application to Lisbon. Omega 36(3):442–450

    Article  Google Scholar 

  • Baum A, Fleming R, Davidson LM (1983) Natural disaster and technological catastrophe. Environ Behav 15(3):333–354

    Article  Google Scholar 

  • Chen A, Yang C, Kongsomsaksakul S, Lee M (2007) Network-based accessibility measures for vulnerability analysis of degradable transportation networks. Netw Spat Econ 7(3):241–256

    Article  Google Scholar 

  • Fan Y, Liu C (2010) Solving stochastic transportation network protection problems using the progressive hedging-based method. Netw Spat Econ 10(2):193–208

    Article  Google Scholar 

  • Farvaresh H, Sepehri MM (2013) A branch and bound algorithm for bi-level discrete network design problem. Netw Spat Econ 13(1):67–106

    Article  Google Scholar 

  • Grotschel M, Monma CL, Stoer M (1995) Design of survivable networks. Handbook in operations research and management science: network models 7. North-Holland, Amsterdam, pp 617–672

  • Holguín-Veras J, Hart WH, Jaller M, Van Wassenhove LN, Pérez N, Wachtendorf T (2012) On the unique features of post-disaster humanitarian logistics. J Oper Manag 30(7–8):494–506

    Article  Google Scholar 

  • Hsu Y-T, Peeta S (2013) Clearance time estimation for incorporating risk in strategies for evacuation operations. Netw Spat Econ. doi:10.1007/s11067-013-9195-5

    Google Scholar 

  • Hwang H, Jernigan JB, Lin YW (2000) Evaluation of seismic damage to Memphis bridges and highway systems. J Bridg Eng 5(4):322–330

    Article  Google Scholar 

  • Jeroslow RG (1985) The polynomial hierarchy and a simple model for competitive analysis. Math Program 32(2):146–164

    Article  Google Scholar 

  • Kerivin H, Mahjoub AR (2005) Design of survivable networks: a survey. Networks 46(1):1–21

    Article  Google Scholar 

  • Kiremidjian AS, Moore J, Basoz N, Burnell K, Fan Y, Hortacsu A (2002) Earthquake risk assessment for transportation systems: analysis of pre-retrofitted system. Proceedings of the 7th National Conference on Earthquake Engineering, EERI, Boston, pp 2109–2116

  • Latora V, Marchiori V (2005) Vulnerability and protection of infrastructure networks. Phys Rev E 71(1):015103R

    Article  Google Scholar 

  • Liu CZ, Fan YY, Ordonez F (2009) A two-stage stochastic programming model for transportation network retrofit. Comput Oper Res 36(5):1582–1590

    Article  Google Scholar 

  • Loh CH, Lee CY, Yeh CH (2003) Seismic risk assessment of transportation system: evaluation immediately after earthquake. Advancing Mitigation Technologies and Disaster Response for Lifeline Systems, ASCE: 123–132

  • Malik K, Mittal AK, Gupta SK (1989) The k most vital arcs in the shortest path problem. Oper Res Lett 8(4):223–227

    Article  Google Scholar 

  • Matisziw TC, Murray AT (2009) Modeling s-t path availability to support disaster vulnerability assessment of network infrastructure. Comput Oper Res 36(1):16–26

    Article  Google Scholar 

  • Matisziw TC, Murray AT, Grubesic TH (2010) Strategic network restoration. Netw Spat Econ 10(3):345–361

    Article  Google Scholar 

  • Moghtaderi-Zadeh M, Der Kiureghian A (1983) Reliability upgrading of lifeline networks for post-earthquake serviceability. Earthq Eng Struct Dyn 11(4):557–566

    Article  Google Scholar 

  • Murray-Tuite PM, Mahmassani HS (2004) Methodology for determining vulnerable links in a transportation network. Transp Res Rec J Transp Res Board 1822:88–96

    Article  Google Scholar 

  • Nagurney A, Qiang Q (2007) A network efficiency measure for congested networks. Europhys Lett 79(3):1–5

    Article  Google Scholar 

  • Peeta S, Salman FS, Gunnec D, Viswanath K (2010) Pre-disaster investment decisions for strengthening a highway network. Comput Oper Res 37:1708–1719

    Article  Google Scholar 

  • Porter K, Ramer K (2012) Estimating earthquake-induced failure probability and downtime of critical facilities. J Bus Contin Emerg Plan 5(4):352–364

    Google Scholar 

  • Ramirez J, Peeta S, Sozen M, Garcia L, Viswanath K (2005) Emergency earthquake routes for the state of Indiana; Part I: Criteria for selection of primary routes: transportation aspects; Part II: Route seismic vulnerability aspects, Technical Research Report FHWA/IN/JTRP-2003/22, Joint Transportation Research Program, Purdue University, 504 p

  • Shapiro A (2001) Monte Carlo simulation approach to stochastic programming. Proceedings of the 2001 Winter Simulation Conference. Arlington, VA, pp 428–431

  • Small E (2000) Examination of alternative strategies for integration of seismic risk considerations in bridge management systems. Transp Res Circ 498(1):E–4

    Google Scholar 

  • Sohn J (2006) Evaluating the significance of highway network links under the flood damage: an accessibility approach. Transp Res A Policy Pract 40(6):491–506

    Article  Google Scholar 

  • Soni S, Pirkul H, Gupta R (1999) Survivable network design: the state of the art. Inf Syst Front 1(3):303–315

    Article  Google Scholar 

  • Sumalee A, Kurauchi F (2006) Network capacity reliability analysis considering traffic regulation after a major disaster. Netw Spat Econ 6(3–4):205–219

    Article  Google Scholar 

  • Towfighi P (1991) Integrated planning for natural and technological disasters. Managing natural disasters and the environment. Environment Department, World Bank, Washington, DC, pp 106–110

    Google Scholar 

  • Ukkusuri SV, Yushimito WF (2009) A methodology to assess the criticality of highway transportation networks. J Transp Secur 2(1–2):29–46

    Article  Google Scholar 

  • Werner SD, Taylor CE, Moore JE (1997) Loss estimation due to seismic risks to highway systems. Earthquake Spectra 13(4):585–604

    Article  Google Scholar 

  • Yao T, Mandala SR, Chung BD (2009) Evacuation transportation planning under uncertainty: a robust optimization approach. Netw Spat Econ 9(2):171–189

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Civil, Architectural, and Environmental Engineering, Illinois Institute of Technology, Chicago, IL, 60616, USA

    Lili Du

  2. School of Civil Engineering, Purdue University, West Lafayette, IN, 47907, USA

    Srinivas Peeta

Authors
  1. Lili Du
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Srinivas Peeta
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Srinivas Peeta.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Du, L., Peeta, S. A Stochastic Optimization Model to Reduce Expected Post-Disaster Response Time Through Pre-Disaster Investment Decisions. Netw Spat Econ 14, 271–295 (2014). https://doi.org/10.1007/s11067-013-9219-1

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11067-013-9219-1

Keywords

Search

Navigation