SpringerLink
Log in

Primary and secondary resonances in pipes conveying fluid with the fractional viscoelastic model

  • Published:
Meccanica Aims and scope Submit manuscript

Abstract

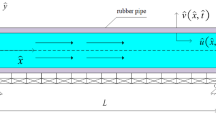
Nonlinear forced vibrations of a fractional viscoelastic pipe conveying fluid exposed to the time-dependent excitations is investigated in the present work. Attention is focused in particular on the primary and secondary resonances with the Kelvin–Voigt fractional order constitutive relationship model. The nonlinear geometric partial differential equations due to stretching effect have been expressed by assumptions with Von Karman’s strain-displacement relation and Euler–Bernoulli beam theory. Viscoelastic fractional model for dam** and stiffness, and also plug flow model for fluid flow are considered to derive the equation of motion. Based on the Galerkin truncation, the coupled Fluid-Solid interaction nonlinear equation transferred to ordinary differential equations. The method of multiple scales is adopted to analyze steady-state solutions for the primary, superharmonic, and subharmonic resonances. Finally, the detailed parametric studies on the nonlinear dynamic behavior are discussed. Results delineate that the fractional derivative order and the retardation time have significant effects on the oscillation exhibited for different values of flow velocity.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
EUR 32.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or Ebook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24
Fig. 25
Fig. 26

Similar content being viewed by others

References

  1. Zhang M, Shen Y, **ao L, Wenzhong Q (2017) Application of subharmonic resonance for the detection of bolted joint looseness. Nonlinear Dyn 88(3):1643–1653

    Google Scholar 

  2. Andreaus U, Baragatti P (2012) Experimental damage detection of cracked beams by using nonlinear characteristics of forced response. Mech Syst Signal Process 31:382–404

    ADS  Google Scholar 

  3. Mohammadi Ghazi R, Büyüköztürk O (2016) Damage detection with small data set using energy-based nonlinear features. Struct Control Health Monit 23(2):333–348

    Google Scholar 

  4. Andreaus U, Baragatti P (2011) Cracked beam identification by numerically analysing the nonlinear behaviour of the harmonically forced response. J Sound Vib 330(4):721–742

    ADS  Google Scholar 

  5. Peng ZK, Lang ZQ, Billings SA (2007) Crack detection using nonlinear output frequency response functions. J Sound Vib 301(3–5):777–788

    ADS  Google Scholar 

  6. Tsyfansky SL, Beresnevich VI (2000) Non-linear vibration method for detection of fatigue cracks in aircraft wings. J Sound Vib 236(1):49–60

    ADS  MATH  Google Scholar 

  7. Paidoussis MP (2014) Fluid-structure interactions : slender structures and axial flow, vol 1, 2nd edn. Elsevier, Amsterdam

    Google Scholar 

  8. Lin Y-H, Tsai Y-K (1997) Nonlinear vibrations of timoshenko pipes conveying fluid. Int J Solids Struct 34(23):2945–2956

    MATH  Google Scholar 

  9. Semler C, Paıdoussis MP (1996) Nonlinear analysis of the parametric resonances of a planar fluid-conveying cantilevered pipe. J Fluids Struct 10(7):787–825

    Google Scholar 

  10. Semler C, Li GX, Paıdoussis MP (1994) The non-linear equations of motion of pipes conveying fluid. J Sound Vib 169(5):577–599

    ADS  MATH  Google Scholar 

  11. Lee S-I, Chung J (2002) New non-linear modelling for vibration analysis of a straight pipe conveying fluid. J Sound Vib 254(2):313–325

    ADS  Google Scholar 

  12. Szabó Z (2003) Nonlinear analysis of a cantilever pipe containing pulsatile flow. Meccanica 38(1):163–174

    MathSciNet  MATH  Google Scholar 

  13. Ni Q, Tang M, Luo Y, Wang Y, Wang L (2014) Internal-external resonance of a curved pipe conveying fluid resting on a nonlinear elastic foundation. Nonlinear Dyn 76(1):867–886

    MathSciNet  MATH  Google Scholar 

  14. Mao X-Y, Ding H, Chen L-Q (2016) Steady-state response of a fluid-conveying pipe with 3: 1 internal resonance in supercritical regime. Nonlinear Dyn 86(2):795–809

    Google Scholar 

  15. Liu Z-Y, Wang L, Sun X-P (2018) Nonlinear forced vibration of cantilevered pipes conveying fluid. Acta Mech Solida Sin 31(1):32–50

    ADS  Google Scholar 

  16. Rong Bao L, **ao-Ting KR, Ni X-J, Tao L, Wang G-P (2018) Nonlinear dynamics analysis of pipe conveying fluid by riccati absolute nodal coordinate transfer matrix method. Nonlinear Dyn 92(2):699–708

    Google Scholar 

  17. Tang Y, Yang T (2018) Post-buckling behavior and nonlinear vibration analysis of a fluid-conveying pipe composed of functionally graded material. Compos Struct 185:393–400

    Google Scholar 

  18. Taylor G, Ceballes S, Abdelkefi A (2018) Insights on the point of contact analysis and characterization of constrained pipelines conveying fluid. Nonlinear Dyn 93(3):1261–1275

    Google Scholar 

  19. Bagley Ronald L, Torvik PJ (1983) A theoretical basis for the application of fractional calculus to viscoelasticity. J Rheol 27(3):201–210

    ADS  MATH  Google Scholar 

  20. Bagley Ronald L, Torvik J (1983) Fractional calculus-a different approach to the analysis of viscoelastically damped structures. AIAA J 21(5):741–748

    ADS  MATH  Google Scholar 

  21. Caputo M, Mainardi F (1971) A new dissipation model based on memory mechanism. Pure Appl Geophys 91(1):134–147

    ADS  MATH  Google Scholar 

  22. Caputo M, Mainardi F (1971) Linear models of dissipation in anelastic solids. La Rivista del Nuovo Cimento (1971–1977) 1(2):161–198

    ADS  Google Scholar 

  23. Oldham K, Spanier J (1974) The fractional calculus theory and applications of differentiation and integration to arbitrary order, vol 111. Elsevier, Amsterdam

    MATH  Google Scholar 

  24. Rossikhin Y, Shitikova MV (2012) On fallacies in the decision between the caputo and Riemann–Liouville fractional derivatives for the analysis of the dynamic response of a nonlinear viscoelastic oscillator. Mech Res Commun 45:22–27

    Google Scholar 

  25. Yang T-Z, Fang B (2012) Stability in parametric resonance of an axially moving beam constituted by fractional order material. Arch Appl Mech 82(12):1763–1770

    MATH  Google Scholar 

  26. Di Paola M, Heuer R, Pirrotta A (2013) Fractional visco-elastic Euler–Bernoulli beam. Int J Solids Struct 50(22–23):3505–3510

    Google Scholar 

  27. Yang Tianzhi, Fang B (2013) Asymptotic analysis of an axially viscoelastic string constituted by a fractional differentiation law. Int J Non-Linear Mech 49:170–174

    Google Scholar 

  28. Baleanu D, Diethelm K, Scalas E, Trujillo JJ (2016) Fractional calculus. World Scientific Publishing Company, Singapore

    MATH  Google Scholar 

  29. Colinas-Armijo N, Cutrona S, Di Paola M, Pirrotta A (2017) Fractional viscoelastic beam under torsion. Commun Nonlinear Sci Numer Simul 48:278–287

    ADS  MathSciNet  Google Scholar 

  30. Permoon MR, Haddadpour H, Javadi M (2018) Nonlinear vibration of fractional viscoelastic plate: primary, subharmonic, and superharmonic response. Int J Non-Linear Mech 99:154–164

    Google Scholar 

  31. Asgari M, Permoon MR, Haddadpour H (2017) Stability analysis of a fractional viscoelastic plate strip in supersonic flow under axial loading. Meccanica 52(7):1495–1502

    MathSciNet  MATH  Google Scholar 

  32. Agrawal OP (2004) Analytical solution for stochastic response of a fractionally damped beam. J Vib Acoust 126(4):561–566

    Google Scholar 

  33. Giuseppe F, Adolfo S, Massimiliano Z (2013) A non-local two-dimensional foundation model. Arch Appl Mech 83(2):253–272

    MATH  Google Scholar 

  34. Di Lorenzo S, Di Paola M, Pinnola FP, Pirrotta A (2014) Stochastic response of fractionally damped beams. Probab Eng Mech 35:37–43

    Google Scholar 

  35. Spanos PD, Malara G (2014) Nonlinear random vibrations of beams with fractional derivative elements. J Eng Mech 140(9):04014069

    Google Scholar 

  36. Wojciech S, Tomasz B, Christian L (2015) Fractional Euler–Bernoulli beams: theory, numerical study and experimental validation. Eur J Mech-A/Solids 54:243–251

    MathSciNet  Google Scholar 

  37. Di Paola M, Scimemi GF (2016) Finite element method on fractional visco-elastic frames. Comput Struct 164:15–22

    Google Scholar 

  38. Jan Kazimierz Freundlich (2016) Dynamic response of a simply supported viscoelastic beam of a fractional derivative type to a moving force load. J Theor Appl Mech 54(4):1433–1445

    Google Scholar 

  39. Gioacchino A, Di Mario P, Giuseppe F, Pinnola FP (2018) On the dynamics of non-local fractional viscoelastic beams under stochastic agencies. Compos Part B Eng 137:102–110

    Google Scholar 

  40. Liaskos KB, Pantelous AA, Kougioumtzoglou IA, Meimaris AT (2018) Implicit analytic solutions for the linear stochastic partial differential beam equation with fractional derivative terms. Syst Control Lett 121:38–49

    MathSciNet  MATH  Google Scholar 

  41. Jan F (2019) Transient vibrations of a fractional Kelvin–Voigt viscoelastic cantilever beam with a tip mass and subjected to a base excitation. J Sound Vib 438:99–115

    Google Scholar 

  42. Sinir BG, Donmez DD (2015) The analysis of nonlinear vibrations of a pipe conveying an ideal fluid. Eur J Mech-B/Fluids 52:38–44

    MathSciNet  MATH  Google Scholar 

  43. Tang Y, Yang T, Fang B (2018) Fractional dynamics of fluid-conveying pipes made of polymer-like materials. Acta Mech Solida Sin 31(2):243–258

    Google Scholar 

  44. Tang Y, Zhen Y, Fang B (2018) Nonlinear vibration analysis of a fractional dynamic model for the viscoelastic pipe conveying fluid. Appl Math Model 56:123–136

    MathSciNet  Google Scholar 

  45. Javadi M, Noorian MA, Irani S (2019) Stability analysis of pipes conveying fluid with fractional viscoelastic model. Meccanica 54(3):399–410

    MathSciNet  Google Scholar 

  46. Amabili Marco (2008) Nonlinear vibrations and stability of shells and plates. Cambridge University Press, Cambridge

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Faculty of Aerospace Engineering, K.N. Toosi University of Technology, Tehran, Iran

    M. Javadi, M. A. Noorian & S. Irani

Authors
  1. M. Javadi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. M. A. Noorian
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. S. Irani
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to M. A. Noorian.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Javadi, M., Noorian, M.A. & Irani, S. Primary and secondary resonances in pipes conveying fluid with the fractional viscoelastic model. Meccanica 54, 2081–2098 (2019). https://doi.org/10.1007/s11012-019-01068-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11012-019-01068-2

Keywords

Search

Navigation