Abstract
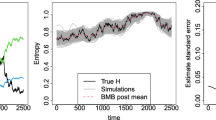
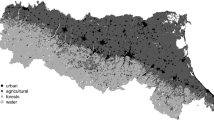
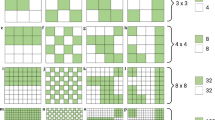
Entropy is widely employed in many applied sciences to measure the heterogeneity of observations. Recently, many attempts have been made to build entropy measures for spatial data, in order to capture the influence of space over the variable outcomes. The main limit of these developments is that all indices are computed conditional on a single distance and do not cover the whole spatial configuration of the phenomenon under study. Moreover, most of them do not satisfy the desirable additivity property between local and global spatial measures. This work reviews some recent developments, based on univariate distributions, and compares them to a new approach which considers the properties of entropy measures linked to bivariate distributions. This perspective introduces substantial innovations. Firstly, Shannon’s entropy may be decomposed into two terms: spatial mutual information, accounting for the role of space in determining the variable outcome, and spatial global residual entropy, summarizing the remaining heterogeneity carried by the variable itself. Secondly, these terms both satisfy the additivity property, being sums of partial entropies measuring what happens at different distance classes. The proposed indices are used for measuring the spatial entropy of a marked point pattern on rainforest tree species. The new entropy measures are shown to be more informative and to answer a wider set of questions than the current proposals of the literature.




Similar content being viewed by others
References
Anselin L (1995) Local indicators of spatial association—LISA. Geogrl Anal 27(2):94–115
Batty M (1974) Spatial entropy. Geogr Anal 6:1–31
Batty M (1976) Entropy in spatial aggregation. Geogr Anal 8:1–21
Batty M (2010) Space, scale, and scaling in entropy maximizing. Geogr Anal 42:395–421
Cover T, Thomas J (2006) Elements of information theory, 2nd edn. Wiley, Hoboken
Karlström A, Ceccato V (2002) A new information theoretical measure of global and local spatial association. Jaharb Regionalwissensc 22:13–40
Leibovici D (2009) Defining spatial entropy from multivariate distributions of co-occurrences. In: Hornsby KS et al. (eds) 9th international conference on spatial information theory 2009. Lecture Notes in Computer Science vol 5756, Springer, Berlin, pp 392–404
Leibovici D, Claramunt C, Guyader DL, Brosset D (2014) Local and global spatio-temporal entropy indices based on distance ratios and co-occurrences distributions. Int J Geogr Inf Sci 28(5):1061–1084
Li H, Reynolds J (1993) A new contagion index to quantify spatial patterns of landscapes. Landscape Ecol 8(3):155–162
O’Neill R, Krummel J, Gardner R, Sugihara G, Jackson B, DeAngelis D, Milne B, Turner M, Zygmunt B, Christensen S, Dale V, Graham R (1988) Indices of landscape pattern. Landscape Ecol 1(3):153–162
Parresol B, Edwards L (2014) An entropy-based contagion index and its sampling properties for landscape analysis. Entropy 16(4):1842–1859
Rajala T, Illian J (2012) A family of spatial biodiversity measures based on graphs. Environ Ecol Stat 19:545–572
Riitters K, O’Neill R, Wickham J, Jones K (1996) A note on contagion indices for landscape analysis. Landscape Ecol 11(4):197–202
Shannon C (1948) A mathematical theory of communication. Bell Syst Tech J 27(379–423):623–656
Stone J (2015) Information Lheory. A tutorial introduction. Sebtel Press, Sheffield
Acknowledgements
This work is developed under the PRIN2015 supported-project ’Environmental processes and human activities: capturing their interactions via statistical methods (EPHASTAT)’ (Grant Number 20154X8K23) funded by MIUR (Italian Ministry of Education, University and Scientific Research).
Asregards author Linda Altieri, the research work underlying this paper was partially funded by the FIRB 2012 (Grant Number RBFR12URQJ) ’Statistical modelling of environmental phenomena: pollution, meteorology, health and their interactions’ for research projects by MIUR (Italian Ministry of Education, University and Scientific Research).
Author information
Authors and Affiliations
Corresponding author
Additional information
Handling Editor: Pierre Dutilleul.
Rights and permissions
About this article
Cite this article
Altieri, L., Cocchi, D. & Roli, G. A new approach to spatial entropy measures. Environ Ecol Stat 25, 95–110 (2018). https://doi.org/10.1007/s10651-017-0383-1
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10651-017-0383-1