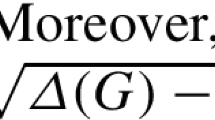Abstract
Let \(F\) be a function from \(\mathbb {F}_{p^n}\) to itself and \(\delta \) a positive integer. \(F\) is called zero-difference \(\delta \)-balanced if the equation \(F(x+a)-F(x)=0\) has exactly \(\delta \) solutions for all nonzero \(a\in \mathbb {F}_{p^n}\). As a particular case, all known quadratic planar functions are zero-difference 1-balanced; and some quadratic APN functions over \(\mathbb {F}_{2^n}\) are zero-difference 2-balanced. In this paper, we study the relationship between this notion and differential uniformity; we show that all quadratic zero-difference \(\delta \)-balanced functions are differentially \(\delta \)-uniform and we investigate in particular such functions with the form \(F=G(x^d)\), where \(\gcd (d,p^n-1)=\delta +1\) and where the restriction of \(G\) to the set of all nonzero \((\delta +1)\)th powers in \(\mathbb {F}_{p^n}\) is an injection. We introduce new families of zero-difference \(p^t\)-balanced functions. More interestingly, we show that the image set of such functions is a regular partial difference set, and hence yields strongly regular graphs; this generalizes the constructions of strongly regular graphs using planar functions by Weng et al. Using recently discovered quadratic APN functions on \(\mathbb {F}_{2^8}\), we obtain \(15\) new \((256, 85, 24, 30)\) negative Latin square type strongly regular graphs.
Similar content being viewed by others
References
Bracken C., Byrne E., Markin N., McGuire G.: On the Walsh spectrum of a new APN function. In: Workshop on Cryptography and Coding. Lecture Notes in Computer Science, vol. 4887, pp. 92–98. Springer, Berlin (2007).
Brouwer A.E.: Online database of strongly regular graphs. http://www.win.tue.nl/~aeb/graphs/srg/srgtab.html.
Brouwer A.E., Haemers W.H.: Structure and uniqueness of the \((81,20,1,6)\) strongly regular graph. Discret. Math. 106(107), 77–82 (1992).
Brouwer A.E., Wilson R.M., **s. J. Complex. 20(2–3), 205–244 (2004).
Carlet C., Ding C., Niederreiter H.: Authentication schemes from highly nonlinear functions. Des. Codes Cryptogr. 40, 71–79 (2006).
Chen E.: Projective binary \([85,8]\) two weight codes (private communication).
Chen E.: Online database of two-weight codes. http://moodle.tec.hkr.se/~chen/research/2-weight-codes/.
Ding C.: Optimal constant composition codes from zero-difference balanced functions. IEEE Trans. Inf. Theory 54(12), 5766–5770 (2008).
Ding C.: Optimal and perfect systems of sets. J. Comb. Theory Ser. A 116, 109–119 (2009).
Ding C., Tan Y.: Zero-difference balanced functions with applications. J. Stat. Theory Pract. 1(6), 3–19 (2012).
Ding C., Wang Q., **s. In: Arithmetic of Finite Fields. Lecture Notes in Computer Science, vol. 5130, pp. 117–122. Springer, Berlin (2008).
Lidl R., Niederreiter H.: Finite Fields. Encyclopedia of Mathematics and Its Applications, vol. 20. Cambridge University Press, Cambridge (1983).
Ma S.L.: A survey of partial difference sets. Des. Codes Cryptogr. 4, 221–261 (1994).
Nyberg K.: Perfect nonlinear S-Boxes. In: Proceedings of EUROCRYPT’91. Lecture Notes in Computer Science, vol. 547, pp. 378–386. Springer, Berlin (1991).
Passman D.S.: The Algebraic Structure of Group Rings. Wiley-Interscience, New York (1977).
Pott A.: Finite geometry and character theory. Lecture Notes in Mathematics, vol. 1601. Springer, Berlin (1995).
Pott A., Tan Y., Feng T., Ling S.: Association schemes arising from bent functions. Des. Codes Cryptogr. 59(1), 319–331 (2011).
Tan Y.: New quadratic APN functions on \({\mathbb{F}}_{2^7}\) and \({\mathbb{F}}_{2^8}\). http://www.ytan.me.
Tan Y., Pott A., Feng T.: Strongly regular graphs associated with ternary bent functions. J. Comb. Theory Ser. A 117(6), 668–682 (2010).
van Dam E.R., Fon-Der-Flaass D.: Codes, graphs, and schemes from nonlinear functions. Eur. J. Comb. 1(24), 85–98 (2000).
Wang Q., Zhou Y.: Sets of zero-difference balanced functions and their applications. Adv. Math. Commun. 8(1), 83–101 (2014).
Weng G., Qiu W., Wang Z., **ang Q.: Pseudo-Paley graphs and skew Hadamard difference sets from presemifields. Des. Codes Cryptogr. 44, 49–62 (2007).
Weng G., Tan Y., Gong, G.: On almost perfect nonlinear functions and their related algebraic objects. In: Proceedings of International Workshop on Coding and Cryptography, pp. 48–57. Springer, Berlin (2013).
Yu Y., Wang M., Li Y.: A matrix approach for constructing quadratic APN functions. In: Proceedings of International Workshop on Coding and Cryptography, pp. 39–47. Springer, Berlin (2013).
Zhou Z., Tang X., Wu D., Yang Y.: Some new classes of zero-difference balanced functions. IEEE Trans. Inf. Theory 58(1), 139–145 (2012).
Acknowledgments
We would like to thank Eric Chen for kindly sending us the generator matrices of the binary \([85,8]\) codes in the database of two-weight codes he maintains and thank Alexander Pott for careful reading of this paper. We also thank the anonymous reviewers for their valuable suggestions which improve this paper. We particularly thank one reviewer for pointing out the relationship between zero-difference balanced functions and optimal constant composition codes, which leads to the results in Remark 5.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by G. McGuire.
Appendix
Appendix
The generating polynomial of the field \(\mathbb {F}_{2^8}\) over \(\mathbb {F}_2\) is \(x^8+x^4+x^3+x^2+1\) (see Table 2).
Rights and permissions
About this article
Cite this article
Carlet, C., Gong, G. & Tan, Y. Quadratic zero-difference balanced functions, APN functions and strongly regular graphs. Des. Codes Cryptogr. 78, 629–654 (2016). https://doi.org/10.1007/s10623-014-0022-x
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10623-014-0022-x