Wait-and-judge scenario optimization

Abstract

We consider convex optimization problems with uncertain, probabilistically described, constraints. In this context, scenario optimization is a well recognized methodology where a sample of the constraints is used to describe uncertainty. One says that the scenario solution generalizes well, or has a high robustness level, if it satisfies most of the other constraints besides those in the sample. Over the past 10 years, the main theoretical investigations on the scenario approach have related the robustness level of the scenario solution to the number of optimization variables. This paper breaks into the new paradigm that the robustness level is a-posteriori evaluated after the solution is computed and the actual number of the so-called support constraints is assessed (wait-and-judge). A new theory is presented which shows that a-posteriori observing k support constraints in dimension $d > k$ allows one to draw conclusions close to those obtainable when the problem is from the outset in dimension k. This new theory provides evaluations of the robustness that largely outperform those carried out based on the number of optimization variables.

Appendices

Appendix 1: The guarantee valid in dimension 1 is unattainable when 1 support constraint is seen in dimension 2

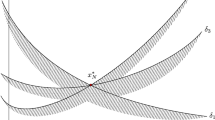
Consider the optimization problem illustrated in Fig. 9 where the probabilistic mass of the V-shaped constraints is p and that of the U-shaped constraints is $1-p$. For a given $\epsilon (1) < p$, the event $\left\{ V(x^*_N) > \epsilon (1) \; \wedge \; s^*_N = 1 \right\}$ is met when all N constraints are U-shaped or when only 1 constraint is V-shaped. This event has probability $(1-p)^N + Np(1-p)^{N-1}$. The $\sup$ of this probability over the p values that satisfy $p > \epsilon (1)$ is $(1-\epsilon (1))^N + N\epsilon (1)(1-\epsilon (1))^{N-1}$. According to (3), this is the probability that $V(x^*_N) > \epsilon (1)$ in a fully-supported problem in dimension 2. This probability is bigger than the probability $(1-\epsilon (1))^N$, let us call it $\beta$, of $V(x^*_N) > \epsilon (1)$ in a fully-supported problem in dimension 1. Hence, for the problem in dimension 2 given in Fig. 9 one has to increase $\epsilon (1)$ to the value $\epsilon '(1)$ such that $(1-\epsilon '(1))^N + N\epsilon '(1)(1-\epsilon '(1))^{N-1} = \beta$ to obtain that the probability of the event $\left\{ V(x^*_N) > \epsilon '(1) \; \wedge \; s^*_N = 1 \right\}$ is bounded by $\beta$.

Next we show that this example constitutes a counterexample to the validity of Eq. (7). To see this, take a generic $\epsilon (1)$ and $\epsilon (0) = \epsilon (2) = 1$. The right-hand side of (7) becomes $(1-\epsilon (1))^N$, which is smaller than

$$\begin{aligned}&{(1-\epsilon (1))^N + N\epsilon (1)(1-\epsilon (1))^{N-1}} \\&\quad = \sup _{p} \mathbb P^N \left\{ V(x^*_N)> \epsilon (1) \; \wedge \; s^*_N=1\right\} \\&\quad = \sup _{p} \left[ \mathbb P^N \left\{ V(x^*_N)> 1 \; \wedge \; s^*_N=0 \right\} \right. \\&\qquad \left. + \mathbb P^N \left\{ V(x^*_N)> \epsilon (1) \; \wedge \; s^*_N=1\right\} + \mathbb P^N \left\{ V(x^*_N)> 1 \; \wedge \; s^*_N=2 \right\} \right] \\&\quad = \sup _{p} \mathbb P^N \left\{ V(x^*_N) > \epsilon (s^*_N) \right\} . \end{aligned}$$

Since $\mathbb P^N \left\{ V(x^*_N) > \epsilon (s^*_N) \right\}$ is the left-hand side of (7), this contradicts (7).

Appendix 2: MATLAB code

The following MATLAB code returns $\epsilon (k) , k=0,1,\dots ,d$, for user assigned d , N, and $\beta$.

Appendix 3: Examples of solutions of Eq. (18)

1.1 Fully-supported problems

One can easily verify that the following $F_k$’s satisfy Eq. (18):

$$\begin{aligned} F_k(v)= & {} \left\{ \begin{array}{ll} 0, &{} \ \ \ v < 1 \\ 1, &{} \ \ \ v \ge 1 \end{array} \right. , \quad k=0,1,\ldots ,d-1, \end{aligned}$$

(40)

$$\begin{aligned} F_d(v)= & {} \left\{ \begin{array}{ll} 0, &{} \ \ \ v < 0 \\ v^d, &{} \ \ \ 0\le v \le 1 \\ 1, &{} \ \ \ v > 1. \end{array} \right. \end{aligned}$$

(41)

These are the $F_k$’s of fully-supported problems. The fact that for fully-supported problems $F_d(v)$ is as in (41) is proven in [12]. To show instead the validity of (40), argue as follows. For $0 \le k < d$, relation

$$\begin{aligned} V(x^*_k) = 1 \end{aligned}$$

(42)

holds with probability one since, otherwise, complementing the set of k constraints with $d-k+1$ other constraints that are satisfied by $x^*_k$, which would be an event with nonzero probability, leads to a total set of $d+1$ constraints among which fewer than d are of support, so contradicting the fully-supportedness assumption. Thus, the measures corresponding to $F_k , k=0,1,\ldots ,d-1$, concentrate in 1. Further, (40) claims that the mass in 1 is equal to 1, which corresponds to say that the number of support constraints is equal to k with probability one. For $k = 0$ this is obvious. For $0< k < d$, this is also true because, if less than k constraints were of support, then at least one of the constraints would be satisfied by the solution generated when only the other constraints are in place, a fact that happens with probability zero since the violation of the solution generated when only the other constraints are in place is equal to 1 as shown in (42).

1.2 Two examples of problems in dimension $d=2$

Consider the problem

$$\begin{aligned}&\min _{x_1 \ge 0, x_2 \ge 0} x_2 \\&\text {subject to: } |x_1 - \delta | \le x_2, \end{aligned}$$

where $\delta$ is uniform in [0, 1]. As it can be easily verified, this problem is fully-supported so that, according to (40),(41), its $F_k$’s are

$$\begin{aligned} F_0(v) = F_1(v) = \left\{ \begin{array}{ll} 0, &{} \ \ \ v< 1 \\ 1, &{} \ \ \ v \ge 1 \end{array} \right. , \quad F_2(v) = \left\{ \begin{array}{ll} 0, &{} \ \ \ v < 0 \\ v^2, &{} \ \ \ 0 \le v \le 1 \\ 1, &{} \ \ \ v > 1 \end{array} \right. . \end{aligned}$$

Consider instead problem

$$\begin{aligned}&\min _{x_1 \ge 0, x_2 \ge 0} x_1+x_2 \\&\text {subject to: } x_{\delta _1} \ge \delta _2, \end{aligned}$$

where $\delta _1$ takes value 1 or 2 with probability 0.5 each, and $\delta _2$ is independent of $\delta _1$ and is uniformly distributed on [0, 1]. This problem is not fully-supported and a simple calculation shows that

$$\begin{aligned}&F_0(v) = \left\{ \begin{array}{ll} 0, &{} \ \ \ v< 1 \\ 1, &{} \ \ \ v \ge 1 \end{array} \right. , \quad F_1(v) = \left\{ \begin{array}{ll} 0, &{} \ \ \ v< 0.5 \\ 2v-1, &{} \ \ \ 0.5 \le v \le 1 \\ 1, &{} \ \ \ v> 1 \\ \end{array} \right. ,\\&\quad F_2(v) = \left\{ \begin{array}{ll} 0, &{} \ \ \ v < 0 \\ 0.5v^2, &{} \ \ \ 0 \le v \le 1 \\ 0.5, &{} \ \ \ v > 1 \end{array} \right. . \end{aligned}$$

These $F_k$’s are another solution of Eq. (18).