The theory of electron transfer

Abstract

This article provides an overview of the theory of electron transfer. Emphasis is placed on the history of key ideas and on the definition of difficult terms. Among the topics considered are the quantum formulation of electron transfer, the role of thermal fluctuations, the structures of transition states, and the physical models of rate constants. The special case of electron transfer from a metal electrode to a molecule in solution is described in detail.

Introduction

Electron transfer is a type of quantum transition, in which an electron delocalizes from one stationary state and localizes in another stationary state, thereby inducing a change in the occupation number of both states. It is observed in many processes that occur in nature and has been widely studied by chemists, physicists, biochemists, and electrical engineers. This article provides an overview of the theory of electron transfer, with a focus on electron transfer from solid electrodes to species dissolved in electrolyte solutions. The general situation is illustrated in Fig. 1.

Fig. 1

Electron transfer from a donor species D to an acceptor species A in an electrolyte solution. In general, D and A may consist of two molecules, or two electrodes, or one molecule and one electrode. Throughout the present work, it is assumed that D and A are surrounded by solvent molecules and electrolyte ions

Across the physical sciences, electron transfer is observed in many different contexts and on many different timescales. In electrochemistry, for example, it is the principal step in corrosion, electroplating, electrowinning, and electrolysis generally. It is also the energy-transducing process in batteries, fuel cells, solar cells, and supercapacitors. In biology, electron transfer plays a crucial role in photosynthesis, respiration, nitrogen fixation, and in many other biochemical cycles. As a result, more than 10% of the structurally characterized proteins in the Protein Data Bank are redox proteins, i.e., proteins that participate in, or catalyze, electron transfer. In environmental science, electron transfer is fundamental to the chemistry of the world’s oceans and to the dispersal and remediation of metals in the natural environment. Finally, electron transfer is central to the emerging new area of molecular electronics.

Interest in electron transfer has grown enormously over the past century, and the development of the field has been aided by contributions from some of the finest minds in science. However, despite its long and intriguing history, I have made no attempt in the present work to summarize the complex interplay of all the various theories that have been suggested at one time or another. That would be an immense undertaking. Instead, I have tried to provide a short, logical introduction to the foundations of the theory, in a form congenial to the nonexpert. How far I have succeeded in that task must be left to the judgment of the reader.

Any description of electron transfer requires knowledge of the behavior and distribution of electrons around atomic nuclei. This fact was realized very shortly after Joseph Thomson confirmed the existence of the electron in 1897 [1]. Indeed, Thomson himself tried to develop an electron theory of valence. However, progress was slow until Niels Bohr developed the first satisfactory dynamic model of an atom in 1913 [2]. In Bohr’s model, each electron was allowed to move in an orbit according to the classical laws of electrostatics, and then some ad hoc assumptions were introduced which had the effect of restricting the electrons to certain energy states, which corresponded to quantized values of angular momentum. A defect of Bohr’s model, however, was that it allowed electrons to have precise values of position and momentum simultaneously, and evidence soon mounted against that. In addition, scattering experiments began to suggest that electrons might have a wavelike character. The resulting intellectual crisis was not resolved until 1926 when Erwin Schrödinger formulated wave mechanics and derived his eponymous equation [3]. It was one of the triumphs of the Schrödinger approach that the existence of discrete energy levels followed from the laws of wave mechanics and not vice versa.

The year after Schrödinger’s work was published, Werner Heisenberg proposed his famous Uncertainty Principle [4]. According to the principle, one can never know the position and momentum of an electron simultaneously. At fixed momentum, we must replace certainty with mere probability that the electron is at a particular location. Mathematically, this means that we must define the location of an electron by means of a probability function. The value of this function necessarily varies from place to place according to the chance that the electron will be found there. If we call this function ρ (rho) and accept that its value might be different in every different volume of space τ (tau), then ρdxdydz (≡ρdτ) is the probability that a single electron will be found in the small volume dτ surrounding the point (x, y, z). For this reason, ρ is called the probability density function. Rather obviously, since the single electron must definitely be somewhere in the totality of space, we also have

$$ \int_{ - \infty }^{ + \infty } {\rho \,{\hbox{d}}\tau = 1} $$

(1.1)

The Born interpretation

A further problem that vexed early researchers was how to connect the probabilistic character of the electron with its wavelike character. Max Born solved this problem in 1926 [5, 6]. If we represent the wave function of an electron by a real number ψ (psi), then according to Born

$$ {\psi^2}\left( {x,y,z} \right) = \rho \left( {x,y,z} \right) $$

(1.2)

This implies that, for a single electron, the square of the wave function at a certain location is just the probability density that the electron will be found there. This is Born’s Statistical Interpretation of the wave function.

Strictly speaking, Eq. 1.2 works only for an electron in a stationary state because it is only in that state that the wave function is a real number. For an electron in a nonstationary state, the wave function becomes a complex number and ψ ² must then be replaced by the square of its modulus |ψ|². Or, what amounts to the same thing, ψ ² must be replaced by ψψ* where ψ* is the complex conjugate of ψ. However, these mathematical nuances need not detain us—they are readily accommodated within the general scheme of quantum mechanics—and anyway we shall return to them later. For present purposes, it is sufficient to note that, in all cases,

$$ \int_{ - \infty }^{ + \infty } {{{\left| \psi \right|}^2}\,{\hbox{d}}\tau = 1} $$

(1.3)

The fact that the probability density ρ(x, y, z) is often concentrated in certain preferred regions of space justifies the well-known interpretation of stationary electronic states as “orbitals” in which the probability of finding the electron is high. In reality, the wave function of an electron stretches to infinity in all directions, and there is always a chance, however small, of finding an electron at an arbitrarily large distance from an atomic nucleus. However, for many purposes, it is often sufficient to note that 90% (say) of the electron’s wave function is concentrated inside a well-defined lobe emanating a short distance from an atom or molecule. The utility of this idea should not be underestimated: as we shall see later on, the ready visualization of the overlap of orbitals provides an intuitive and easy-to-grasp method of deciding if electron transfer will occur or not.

Pathways and probabilities

One of the properties of quantum mechanics that is deeply counterintuitive is the rule for combining probabilities. It is the wave functions that are additive, not the probabilities. This leads to some very peculiar outcomes compared with everyday experience. Suppose, for example, that an electron is able to transfer from a donor species D to an acceptor species A. And suppose, furthermore, that there are two possible pathways between D and A, which for convenience we shall call pathway 1 and pathway 2. Then, it is of some importance to know how these probabilities combine.

Adopting an obvious notation, let us call the probability of electron transfer P ₁ if only pathway 1 is open and P ₂ if only pathway 2 is open. Now, we ask what would happen if both pathways were open at the same time. One might guess that the combined probability of electron transfer would be

$$ {P_{1 + 2}} = {P_1} + {P_2} $$

(1.4)

But that would be wrong! In fact, the combined probability of electron transfer is

$$ {P_{1 + 2}} = {\left| {\,{\psi_1} + {\psi_2}} \right|^2} $$

(1.5)

which may be less than either P ₁ or P ₂ alone. In other words, opening a second pathway may actually cause a decrease in overall probability for electron transfer. Indeed, this is routinely observed whenever there is destructive interference between the wave functions ψ ₁ and ψ ₂. It follows that tremendous care must be taken when tracing multiple pathways of electron transfer through complex systems. To avoid problems of this type, we shall, for the remainder of this document, confine our attention to electron transfer events that proceed through single pathways between donor species and acceptor species.

The Schrodinger equation

At the deepest level, the Schrödinger equation is just the quantum equivalent of the conservation of energy. Classically, the conservation of energy states that

$$ T + V = E $$

(1.6)

where T and V are the kinetic energy and potential energy of the system under consideration, and E is the total energy. For example, for a single electron of mass m moving along the x-axis in an electric field such that its electrostatic potential energy is V(x), Eq. 1.6 would read

$$ \frac{1}{2}m{\dot x^2} + V(x) = E $$

(1.7)

or, defining the momentum ${p_{\rm{x}}} = m\dot x$,

$$ \frac{{p_{\rm{x}}^2}}{{2m}} + V(x) = E $$

(1.8)

Classically, the solution of this last equation gives the motion (orbit) of the electron. However, in quantum mechanics, the same equation is converted into a wave equation by means of a Hamiltonian transformation (see Table 1).

Table 1 Hamiltonian transformations relevant to quantum mechanics

Thus, converting to Hamiltonian operators,

$$ H = - \frac{{{\hbar^2}}}{{2m}}\,\frac{{{\partial^2}}}{{\partial {x^2}}} + V(x) $$

(1.9)

and so

$$ H\psi = - \frac{{{\hbar^2}}}{{2m}}\,\frac{{{\partial^2}\psi }}{{\partial {x^2}}} + V(x)\,\psi $$

(1.10)

Hence, for the time-independent case, we have

$$ H\psi = E\psi $$

(1.11)

and for the time-dependent case we have

$$ H\psi = \left( {i\hbar } \right)\,\frac{{\partial \psi }}{{\partial t}} $$

(1.12)

These are the textbook forms of the Schrödinger equation. In electron transfer theory, we are mainly concerned with the time-dependent form, Eq. 1.12.

Equation 1.12 is a homogeneous linear partial differential equation. (Homogeneous because every term depends on ψ; linear because there are no powers higher than the first.) Perhaps the most surprising feature of this equation is that it has an infinite number of solutions, with each solution representing a possible state of the system. Such an overabundance of outcomes leads to a natural question: if there are infinitely many solutions, which one is appropriate in a given circumstance? Actually, the answer is determined by the initial and boundary conditions of the problem. At room temperature, however, we are mostly concerned with the lowest energy solution, commonly known as the ground-state solution. It is also natural to ask whether mathematical solutions of the Schrödinger equation can be obtained in simple, closed forms. The answer is, generally, no. In most cases, solutions are obtained as infinite series whose coefficients must be determined by recurrence relations.

The Born–Oppenheimer approximation

Closed-form solutions of the time-dependent Schrödinger equation are possible only for certain special cases of the electrostatic potential energy V(x). It is particularly unfortunate that the Schrödinger equation is insoluble for all cases where an electron moves under the influence of more than one atomic nucleus, as in electron transfer. However, the equation may be simplified by noting that atomic nuclei have much greater masses than electrons. (Even a single proton is 1,836 times heavier than an electron.) Thus, in classical terms, an electron may be considered to complete several hundred orbits while an atomic nucleus completes just one vibration. An immediate corollary is that, to a good level of approximation, atomic nuclei may be considered motionless while an electron completes a single orbit in a single stationary state. This approximation, known as the Born–Oppenheimer approximation, greatly simplifies the solution of the Schrödinger equation and finds particular use in the solution of computationally intensive problems.

Today, the Born–Oppenheimer approximation is widely used in computer simulations of molecular structure. Assuming the approximation holds, then the system energy may be calculated uniquely for every possible position of the atomic nuclei (assumed motionless). This then allows one to construct a plot of total energy as a function of all the nuclear coordinates, yielding a multidimensional “potential energy surface” for the system under study. The contributing factors to this potential energy surface are

• 1. The Coulomb attractions between the electrons and the nuclei

• 2. The Coulomb repulsions between the electrons

• 3. The Coulomb repulsions between the nuclei

• 4. The kinetic energy of the electrons

It is immediately clear that this is not a true potential energy at all because it contains a mixture of potential energy and kinetic energy terms. However, it does determine the position of lowest potential energy of the atomic nuclei, and so the name is not entirely unreasonable.

Remark

The Coulomb attraction between electrons and nuclei is the only attractive force in the whole of chemistry.

The application of computer simulation methods to electron transfer systems raises the question of precisely what is meant by a “system.” Roughly speaking, there are two different answers to this question, depending on one’s point of view. The minimalist view is that the system consists of the donor and acceptor species only. In that case, there is no “friction” (interaction) between the system and the rest of the solution, and consequently the donor and acceptor species conserve their joint energy at all times. As they mutually interact, potential energy may be converted into kinetic energy, or kinetic energy may be converted into potential energy, but the total remains constant, and the system performs deterministic motions along the potential energy profile. Although unphysical, except perhaps in vacuo, this situation is comparatively easy to program on modern computers and has nowadays attained a certain level of acceptability. The alternative view is that the system consists of the donor and acceptor species plus the entirety of the surrounding solution (sometimes called the “heat bath”). In the latter case, there is continual friction (interaction) between the system and the solution, and accordingly the energies of the donor and acceptor species fluctuate wildly. This is more realistic but requires the use of Gibbs energy profiles rather than potential energy profiles to characterize the system and also makes the motion of the system along the reaction coordinate a stochastic (random) variable. Notwithstanding these complications, we have standardized on Gibbs energy profiles throughout the present work.

Remark

The most probable path between the reactants and products across the Gibbs energy profile is called the reaction coordinate, and the maximum energy along this path is called the Gibbs energy of activation.

For a nonconcerted single-step reaction, beginning at thermodynamic equilibrium and ending at thermodynamic equilibrium, the Gibbs energy of activation is supplied by just one degree of freedom of the system. In this primitive case, the reaction coordinate may be defined in the following convenient way.

Definition

For a nonconcerted single-step reaction, the reaction coordinate is just the extensive variable of the single degree of freedom that takes the system to its transition state. This might be, for example, the length of a single chemical bond or the electrical charge on the ionic atmosphere of an ion.

Remark

For a concerted reaction, the reaction coordinate is necessarily a combination of extensive variables. This is the case, for example, when electron transfer is accompanied by bond rupture, a situation that is outside the scope of the present work.

Tunneling

We now come to the fundamental mechanism of quantum transitions between stationary states. I refer, of course, to tunneling. Among the many outstanding successes of quantum theory over the past 80 years, surely the most impressive has been the discovery of tunneling. Tunneling is the quantum mechanical process by which an electron (or any other light particle) penetrates a classically forbidden region of space and thus transfers between two separate points A and B without localizing at any point in between. For electrons, a “classically forbidden” region of space simply means a region of negative electrostatic potential.

The theory of electron tunneling was initiated by Friedrich Hund in a series of papers published in Zeitschrift für Physik in 1927, where he called the effect “barrier penetration” [7–9]. However, his focus was on the tunneling of electrons between the wells of a double-well potential in a single molecule, so the results were not of immediate transferability to electron transfer between molecules. A more widely applicable theory of tunneling appeared 1 year later. In 1928, Ralph Fowler and Lothar Nordheim explained, on the basis of electron tunneling, the main features of electron emission from cold metals [10]. They were motivated by the fact that electron emission could be stimulated by high electric fields, a phenomenon that had deeply puzzled scientists since its first observation by Robert Wood in 1897 [11]. Also in 1928, Edward Condon and Ronald Gurney proposed a quantum tunneling interpretation of alpha-particle emission [12, 13], which led to widespread acceptance of the tunneling concept. Today, electron tunneling is recognized as crucially important throughout chemistry, biology, and solid-state and nuclear physics.

Before proceeding further, we must also say a few words about the Franck–Condon principle, which applies to most cases of electron tunneling. The principle states that, to a good level of approximation, all the atomic nuclei in a reacting system are effectively motionless while the process of electron tunneling takes place. James Franck and E.G. Dymond initially recognized a special case of this principle in their studies of the photoexcitation of electrons in 1926 [14]. Edward Condon then generalized the principle beyond photochemistry in a classic 1928 Physical Review article entitled “Nuclear Motions Associated with Electron Transitions in Diatomic Molecules” [15]. Although the Franck–Condon principle may be justified by arguments similar to those that are used to justify the Born–Oppenheimer approximation, it has a much wider scope, as the following “plain English” definitions make clear.

Definition

The Born–Oppenheimer approximation is the approximation that, in a system of electrons and nuclei, the atomic nuclei may be considered motionless while an electron makes a single orbit of a single stationary state.

Definition

The Franck–Condon principle is the approximation that, in a system of electrons and nuclei, the atomic nuclei may be considered motionless while an electron makes a quantum transition between two stationary states.

Besides the Born–Oppenheimer approximation and the Franck–Condon principle, several other methods of approximation have been developed to help solve the Schrödinger equation. The most important of these is called time-dependent perturbation theory. As we have already mentioned, it is impossible to find exact solutions of the Schrödinger equation for electrostatic potential energies of even moderate complexity. However, time-dependent perturbation theory allows some complex cases to be solved by first solving simpler cases and then modifying the results incrementally. The method was perfected by Paul Dirac in 1927 [16]. Besides introducing an efficient notation, Dirac also established an important criterion for successful electron transfer—an electron will localize in an acceptor species only if it has the same energy as it did in the donor species.

Dirac’s ideas were introduced into electrochemistry by Ronald Gurney in 1931 [17]. Gurney provided a very clear picture of how an electron transfer event occurs. An electron initially resides in a stationary electronic state of a chemical species, which we identify as the donor. Nearby, an empty electronic state exists inside a second chemical species, which we identify as the acceptor. Due to random fluctuations of the electrostatic potential energy of both species, the energies of both states are momentarily equalized, at which point, the wave function of the electron begins to build up on the acceptor. By the Born interpretation, this means that the probability of finding the electron builds up on the acceptor. When averaged over a whole population of donor and acceptor species, the rate of this buildup corresponds to the rate of electron transfer. In a vacuum, there are of course no random fluctuations of electrostatic potential energy and so the coincidence of donor and acceptor energy states is highly improbable. But, in an electrolyte solution, there are so many random fluctuations of electrostatic potential energy that coincidences of electron energy states occur billions of times every second.

To what extent do random fluctuations of electrostatic potential energy in solution affect the energy of an electron inside a molecule? Gurney answered this question with wonderful clarity. Suppose that an electron resides in the nth energy level of a certain molecule, where it experiences an electrostatic potential energy V(x, y, z). Call its energy w _n. Then, what we want to know is how this energy changes to a new value $w_{\rm{n}}\prime$ when the electrostatic potential energy of the surrounding ionic atmosphere changes to a new value V(x, y, z) + v(x, y, z). The precise answer involves an integration over the whole of space, thus

$$ w_{\rm{n}}\prime - {w_{\rm{n}}} = \int_{ - \infty }^{ + \infty } {\psi_{\rm{n}}^*\,v{\psi_{\rm{n}}}{\hbox{d}}\tau } $$

(1.13)

$$ w_{\rm{n}}\prime - {w_{\rm{n}}} = \int_{ - \infty }^{ + \infty } {v{{\left| {{\psi_{\rm{n}}}} \right|}^2}\,{\hbox{d}}\tau } $$

(1.14)

However, an approximate (but still sufficiently accurate) answer can be obtained by noting that the spatial variation of electrostatic potential energy occurs over long range. For comparison, the potential energy of two charges q ₁ and q ₂ a distance r apart varies as r ⁻¹, whereas the electron density in orbitals decays near-exponentially with r. With such a disparity of length scales, it is reasonable to assume that v(x, y, z) is spatially uniform when evaluating the integral. In that case, v(x, y, z) ≠ f(τ), and

$$ w_{\rm{n}}\prime - {w_{\rm{n}}} \approx v\,\int_{ - \infty }^{ + \infty } {{{\left| {{\psi_{\rm{n}}}} \right|}^2}d\tau } $$

(1.15)

$$ w_{\rm{n}}\prime - {w_{\rm{n}}} \approx v $$

(1.16)

So the answer to our question is that the energy of an electron inside a molecule fluctuates by the same amount as the electrostatic potential energy of the surrounding ionic atmosphere. For this reason, the energy of an electron inside an electrolyte solution bounces up and down like a cork in the ocean.

Yet another fascinating question is, “What is the intrinsic timescale of electron tunneling?” While it is not yet possible to give a final answer, we can estimate that the buildup of an electron’s wave function inside an acceptor species in an electrolyte solution typically occurs on a timescale of <1.0 fs. This timescale is determined by the inertia of the “sea of electrons” in the surrounding medium, which must equilibrate with the newly occupied state. Such a timescale is at the limit of present-day measurements and is exceptionally fast compared with transition-state lifetimes, which are typically on the 10–100-fs timescale. Because of this disparity of time scales, the rate-determining step in many-electron transfer reactions is commonly the environmental reorganization needed to equalize the energies of the donor and acceptor states, rather than the buildup of the wave function itself. For this reason, electron transfer is often referred to as a “mixed” classical–quantum phenomenon.

In summary, electron transfer requires the energies of two electronic states to be made equal. In electrolyte solutions, the equalization process occurs by random fluctuations of the electrostatic potential energies of both reactive species. The fluctuations are spontaneous; they are driven by heat; and they occur even at thermodynamic equilibrium. They are, indeed, equilibrium fluctuations. It is therefore to this topic that we turn first.

Fluctuations in electrolyte solutions

In this section, we seek to identify, and quantify, the fluctuations that trigger electron transfer in electrolyte solutions. We do this on the assumption that the fluctuations are drawn from the same distribution as those that occur at equilibrium.

Before beginning, let us briefly define what we mean by an electrolyte solution. An electrolyte is any neutral substance that dissociates into mobile ions when dissolved in a solvent. Thus, an electrolyte solution may be any mixture of mobile ions dissolved in a solvent. Compared with an ideal solution, an electrolyte solution has an additional degree of freedom, namely, an ability to store energy by microscopic displacements of charge.

In 1878, James Clerk Maxwell [18] defined thermodynamics as

... the investigation of the dynamical and thermal properties of bodies, deduced entirely from what are called the first and second laws of thermodynamics, without any hypotheses as to the molecular constitution of the bodies.

By contrast, kinetic theories require molecular information. In this section, we shall try, in the spirit of Maxwell, to see how much we can learn about the theory of equilibrium fluctuations, without explicitly introducing molecular information. While such an approach necessarily excludes the evaluation of rates, nevertheless, it provides powerful insights into the kinds of fluctuations that trigger electron transfer and supplies some stringent bounds on the kinetic theory.

Equipartition of energy

At thermodynamic equilibrium, all classical systems experience fluctuations of energy whose magnitude, on average, is ½ k _B T per degree of freedom. This is John James Waterston’s famous equipartition of energy [19]. In the case of electron transfer in an electrolyte solution, both the donor and the acceptor species are surrounded by small volumes of solution that experience such fluctuations, and, in fact, it is these that create the transition state for the electron transfer process. For this reason, it is of utmost importance to describe, and quantify, the various types of fluctuation that occur at equilibrium in electrolyte solutions.

Consider a small system embedded in a much larger system (the heat bath). The situation is illustrated in Fig. 2. The intensive parameters that characterize the small system are T (temperature), P (pressure), f (mechanical force), and ϕ (electric potential). Fluctuations of internal energy are denoted ΔU.

Fig. 2

A small system surrounded by a heat bath. Equilibrium fluctuations of internal energy ΔU have a large effect on the small system but a negligible effect on the large system. As a result, the heat bath retains uniform and constant values of all of its intensive parameters whereas the small system does not

We assume that the small system is so tiny that equilibrium fluctuations in its thermodynamic parameters cannot be neglected. Conversely, we assume that the heat bath is so large that equilibrium fluctuations in its thermodynamic parameters can be neglected. The heat bath is also assumed to be isolated from the external world.

Remark

As shown by Boltzmann, equilibrium fluctuations of the intensive parameters of a small system embedded inside a large system form a stationary ergodic process. That is to say, the time-averaged values of the intensive parameters of the small system are identical to the space-averaged values of the intensive parameters of the large system. If it were not so, equilibrium would not be achieved.

From the first law of thermodynamics (the conservation of energy), we know that any fluctuation in the internal energy of the small system ΔU must be accompanied by a complementary fluctuation in the internal energy of the heat bath ΔU _HB,

$$ \Delta U = - \Delta {U_{\rm{HB}}} $$

(2.1)

Further, any fluctuation in the volume of the small system ΔV must likewise be accompanied by a complementary fluctuation in the volume of the heat bath ΔV _HB,

$$ \Delta V = - \Delta {V_{\rm{HB}}} $$

(2.2)

This latter relation might be called the “no-vacuum” condition. To understand its importance, consider what would happen if the small system shrank, but the large system did not expand by the same amount. Then, a vacuum would appear between the two systems, and thermal and hydraulic contact would be lost. Thus, a necessary property of a perfect heat bath is that it does not lose thermal or hydraulic contact with the small system inside it.

We begin our analysis by noting that, for a fluctuated small system having intensive values (T, P, f, ϕ), any infinitesimal increments in the internal energy U _fluc can be written

$$ {\hbox{d}}{U_{\rm{fluc}}} = + T{\hbox{d}}S - P{\hbox{d}}V + f{\hbox{d}}L + \varphi {\hbox{d}}Q $$

(2.3)

Here, S is entropy; V is volume; L is extension; and Q is charge. In addition, T is absolute temperature; P is pressure; f is tension/compression force; and ϕ is electrostatic potential. We see that each of the terms on the right-hand side of Eq. 2.3 is the product of an intensive quantity (T, P, f, ϕ) and the derivative of an extensive quantity (S, V, L, Q). The full equation tells us that, in principle, we can change the internal energy of the small system in various ways, e.g., by changing its entropy S, by changing its volume V, by distorting it through a distance L, or by changing its electric charge Q. The absolute magnitudes of the corresponding internal energy changes are then determined by the sizes of the intensive quantities (T, P, f, ϕ). For example, if we increase the charge on the small system by dQ, then the increase in internal energy is large if the electrostatic potential ϕ is large and small if the electrostatic potential is small.

Thermodynamic availability

In the next step, we must connect the behavior of the small system after it has fluctuated with the behavior before it has fluctuated. In the latter case, the small system has temperature T ₀; pressure P ₀; tension/compression force f ₀; and electrostatic potential ϕ ₀. (The subscript “0” indicates the parameter values of the unfluctuated system.) Under “unfluctuated” conditions, any infinitesimal increments in the internal energy U _unfluc can be written

$$ {\hbox{d}}{U_{\rm{unfluc}}} = + {T_0}{\hbox{d}}S - {P_0}{\hbox{d}}V + {f_0}{\hbox{d}}L + {\varphi_0}{\hbox{d}}Q $$

(2.4)

and therefore the difference in internal energy between the fluctuated small system and the unfluctuated small system is

$$ {\hbox{d}}{U_{\rm{fluc}}} - {\hbox{d}}{U_{\rm{unfluc}}} = {\hbox{d}}\Phi $$

(2.5)

In a somewhat different context, the parameter Φ (phi) was termed the “availability” by Joseph Keenan in 1951 [20]. In engineering texts, it is also sometimes known as the “exergy” of the overall system, a term coined by Zoran Rant [21]. Regardless of what one calls it, the thermodynamic potential Φ is the natural potential for quantifying the energy that fluctuates reversibly back and forth between a small system and a large one. Thus, Φ is the natural potential for quantifying the equilibrium fluctuations in electron transfer theory (and, indeed, in chemical rate theory).

Remark

The thermodynamic potential Φ (availability, exergy) is the proper measure of the energy gained by a small system as it experiences an equilibrium fluctuation inside a much larger system (heat bath).

The essential difference between the internal energy and the available energy is obvious from the following definitions.

Definition

Internal energy (U) is the total energy of a stationary system that can be dissipated into a vacuum by nonnuclear processes.

Definition

Available energy (Φ) is the total energy of a stationary system that can be dissipated into a heat bath by nonnuclear processes.

Now let T, P, f, and ϕ be the temperature, pressure, tension/compression force, and electrostatic potential of the fluctuated small system inside the heat bath, and let T ₀, P ₀, f ₀, and ϕ ₀ be the temperature, pressure, tension/compression force, and electrostatic potential of the unfluctuated small system inside the heat bath. Then, by definition,

$$ \begin{array}{*{20}{c}} \Phi { = {U_{\rm{fluc}}} - {U_{\rm{unfluc}}}} \\{}{ = U\left( {T,P,f,\varphi } \right) - U\left( {{T_0},{P_0},{f_0},{\varphi_0}} \right)} \\\end{array} $$

(2.6)

Because Φ is a function of state, its differential is exact. Hence,

$$ {\hbox{d}}\Phi = {\hbox{d}}{U_{\rm{fluc}}} - {\hbox{d}}{U_{\rm{unfluc}}} $$

(2.7)

For a system having n degrees of freedom, we know from the first law of thermodynamics that the detailed expression for dΦ must contain one heat term (T − T ₀)dS plus (n − 1) work terms of the form (Y − Y ₀)dX. That is,

$$ {\hbox{d}}\Phi = \left( {T - {T_0}} \right){\hbox{d}}S + \sum\limits_{n - 1} {\left( {{Y_{n - 1}} - {Y_0}} \right)\,{\hbox{d}}{X_{n - 1}}} $$

(2.8)

Such a system has 2n primary variables arranged in conjugate pairs whose products have the dimensions of energy. Examples of such conjugate pairs are (P, V) and (ϕ, Q). In each case, the extensive variables are the independent variables. For chemical species in solution, the work terms are predominantly mechanical (vibrational–librational) or electrical in character.

For small n, Eq. 2.8 looks reassuringly benign. But, as n increases, the formula for Φ rapidly becomes unmanageable. Large values of n arise naturally in complex systems because large numbers of vibrational modes are available. Indeed, it is well known that all nonlinear molecules having N atoms have 3N–6 vibrational degrees of freedom, so that, for example, a redox protein has almost as many vibrational modes as it does atoms. (And even a “small” electron transport protein like rubredoxin contains 850 atoms!) To keep the theory of electron transfer within manageable bounds, we shall therefore find it convenient to limit our attention to four representative extensive variables, namely S, V, L, and Q. This allows us to consider four different types of activation process (thermal, hydraulic, mechanical, and electrical) for electron transfer, without becoming bogged down in detail. Thus, we consider

$$ \begin{array}{*{20}{c}} {{\hbox{d}}\Phi }{ = \left( {T - {T_0}} \right){\hbox{d}}S + \sum\limits_{n - 1} {\left( {{Y_{n - 1}} - {Y_0}} \right){\hbox{d}}{X_{n - 1}}} } \\{}{ = \left( {T - {T_0}} \right){\hbox{d}}S - \left( {P - {P_0}} \right){\hbox{d}}V + \left( {f - {f_0}} \right){\hbox{d}}L + \left( {\varphi - {\varphi_0}} \right){\hbox{d}}Q} \\\end{array} $$

(2.9)

We can immediately simplify this formula by noting that the unfluctuated state is at both mechanical equilibrium (mechanoneutrality) and electrostatic equilibrium (electroneutrality). Hence, f ₀ = 0 and ϕ ₀ = 0, so that

$$ {\hbox{d}}\Phi = \left( {T - {T_0}} \right){\hbox{d}}S - \left( {P - {P_0}} \right){\hbox{d}}V + f{\hbox{d}}L + \varphi {\hbox{d}}Q $$

(2.10)

Formulas for the mean square values of the fluctuations that occur in the extensive quantities (ΔS, ΔV, ΔL, ΔQ) of a small system inside a heat bath are readily derived from Eq. 2.10 and are collected in Table 2. These formulas are also of interest in nanotechnology because they set limits on the deterministic behavior of nanoscale devices.

Table 2 Mean square values of the fluctuations that occur in the extensive quantities (ΔS, ΔV, ΔL, ΔQ) of a small system inside a heat bath

At the moment of electron transfer, conservation of energy dictates that the availability of the reactants should match the availability of the products. At this special point, we refer to the value of the availability as the availability of activation and label it by an asterisk; thus,

$$ \Phi * = \left( {U - {U_0}} \right)* $$

(2.11)

In an analogous way, we label the entropy of activation as (S − S ₀)*, the volume of activation as (V − V ₀)*, the extension of activation as (L − L ₀)*, and the charge of activation as (Q − Q ₀)*. In general, we expect all of these parameters to be finite.

Gibbs energy manifold

At constant temperature and pressure of the heat bath (i.e., under “normal” laboratory conditions), it is more usual for chemists to think in terms of Gibbs energy rather than availability. We can readily convert to Gibbs energy by means of a Legendre transform of Eq. 2.11. Thus,

$$ {\hbox{d}}\left( {G - {G_0}} \right) = - \left( {S - {S_0}} \right){\hbox{d}}T + \left( {V - {V_0}} \right){\hbox{d}}P + f\,{\hbox{d}}L + \varphi \,{\hbox{d}}Q $$

(2.12)

Since there are four different terms on the right-hand side of this equation, we may think of the Gibbs energy difference (G − G ₀) as a four-dimensional manifold whose space is randomly explored by the various combinations of fluctuations that occur along the four axes (T, P, L, and Q). However, the most important path through this manifold is the one that maximizes the probability of reaching the product state. This path is called the “reaction coordinate.”

In chemical kinetics, the temperature and pressure of the transition state are assumed to be the same as those of the reactant and product states. This means that dT = 0 and dP = 0 along the reaction coordinate, so that two full terms disappear from Eq. 2.12, leaving only

$$ {\hbox{d}}{\left( {G - {G_0}} \right)_{\rm{RC}}} = f\,{\hbox{d}}L + \varphi \,{\hbox{d}}Q $$

(2.13)

The situation is shown schematically in Fig. 3. The Gibbs energy along the reaction coordinate is a function of L and Q, but not of T and P. Notice also that the transition state occurs at a point which is a maximum along the reaction coordinate but a minimum along all other coordinates.

Fig. 3

Schematic diagram of the most probable path through the four-dimensional manifold of Eq. 2.12, at constant temperature and pressure of the heat bath. Fluctuations of the temperature and pressure of the small system still occur, but they are orthogonal to the reaction coordinate and so do not contribute to the activation process. The transition state is indicated by the asterisk

Remark

Despite the disappearance of the entropy and volume terms from Eq. 2.12, we emphasize that (S − S ₀) and (V − V ₀) are not necessarily 0 along the reaction coordinate. On the contrary, they most likely have finite (and, in principle, measurable) values. It is simply that their conjugate parameters dT and dP are 0.

If we now write the Gibbs energy difference in the form

$$ {\left( {G - {G_0}} \right)_{\rm{RC}}} = \Delta {G_{\rm{RC}}} $$

(2.14)

and integrate Eq. 2.13, we obtain

$$ \Delta {G_{\rm{RC}}} = \int_{\,L} {f{\hbox{d}}L} + \int_{\,Q} {\varphi \,{\hbox{d}}Q} \,\,\, $$

(2.15)

This equation is valid provided only that the heat bath is maintained at constant temperature and pressure. Being thermodynamic, it is also entirely model free. Indeed, it subsumes all known models of electron transfer that use classical equilibrium fluctuations to equalize the energies of reactants and products.

In Eq. 2.15, an important limiting case is observed if f = 0, that is, if the reactants and their inner solvation shells are not distorted during the electron transfer process. In that case, the only fluctuations that are needed to trigger electron transfer are fluctuations of charge in the ionic atmosphere of the reactants. The Gibbs energy profile becomes one dimensional, and the reaction coordinate becomes the charge Q. (The charge fluctuation model [22].)

Remark

∆G _RC is the parameter that is sketched in innumerable “Gibbs energy plots” in the electrochemical literature.

It follows from the above analysis that the activation energy for electron transfer may be expressed in the generic form

$$ \Delta G_{\rm{RC}}^{*} = \int_0^{{L^*}} {f\,{\hbox{d}}L} + \int_0^{{Q^*}} {\varphi \,{\hbox{d}}Q} $$

(2.16)

where the asterisk once again indicates the transition state. This formula, which plays the role of a “master equation,” may also be incorporated directly into transition-state theory (TST).

Transition-state theory

Transition-state theory is one of the most enduring theories of chemical reactions in solution. It is based on the idea that an “energy barrier” exists between reactants and products. The original concept may be traced back to the researches of René Marcelin [23], published posthumously in 1915, although most modern formulations are actually derived from the work of Henry Eyring, Meredith Evans, Michael Polanyi, and Eugene Wigner published in the 1930s [24–26]. Today, the popularity of TST rests on its ability to correlate reaction rates with easily measured quantities such as temperature and concentration.

Many different versions of transition-state theory have evolved over time, but most of them share the following assumptions (at constant temperature and pressure):

• 1. There is thermodynamic equilibrium between all the degrees of freedom of the system, with the exception of those that contribute to the reaction coordinate.

• 2. The transition state occurs at a Gibbs energy maximum along the reaction coordinate, but at a Gibbs energy minimum along all other coordinates.

• 3. Electrons behave according to quantum laws while nuclei behave according to classical laws (i.e., nuclear tunneling is disallowed).

• 4. The rate of reaction never exceeds the response rate of the heat bath.

• 5. The rate of reaction is proportional to the number of nuclei in the transition state.

• 6. The rate of reaction is proportional to the rate that individual nuclei leave the transition state in the forward direction.

In electron transfer theory, all of these assumptions carry over, except for the last. Regarding the last assumption, the rate that individual nuclei leave the transition state must be replaced by the rate at which the electron probability builds up on the acceptor.

In transition-state theory, the rate constant for electron transfer (k _et) takes the form

$$ {k_{\rm{et}}} = {k_0}\exp \left( {\frac{{ - \Delta G_{\rm{RC}}^{*}}}{{RT}}} \right) $$

(2.17)

Here, k ₀ is the maximum rate constant and $\Delta G_{\rm{RC}}^{*}$ is the activation energy given by Eq. 2.16. When Eq. 2.17 is combined with Eq. 2.16, we see immediately that electron transfer requires at most just two types of thermodynamic fluctuation (thermodynamic work) in order to be activated, namely (1) elastic distortions of the donor and acceptor species, which take place against their internal force fields, and (2) electrostatic charge injections into the environment of the donor and acceptor species, which take place against the self-repulsions of the charges.

These are powerful insights. However, while the laws of thermodynamics reveal the kinds of energy fluctuations that can trigger electron transfer, the same laws reveal nothing about the structure of a given transition state or the structure of the electrolyte solution that surrounds it. Progress in those areas forms the subject of the next section.

Transition states in electrolyte solutions

In order to understand the structure of transition states in electrolyte solutions, we must first understand the structure of electrolyte solutions. Here, we provide a minimum account of this area, up to and including the theory of solvation. We then proceed to describe the evolution of ideas about “inner-sphere” and “outer-sphere” electron transfer processes.

In the late nineteenth century, the theory of solutions was developed by analogy with the theory of ideal gases. The solute was regarded as a set of uncharged spherical particles, and the solvent was regarded as an inert continuum through which the particles moved at random. Individual particles were assumed to be independent, and their mutual interaction was assumed to be negligible. For nonionic species, some minor success was achieved by this approach. For ionic species, however, the method proved wholly inadequate.

Today, we know why the “ideal solution” approach failed. Firstly, the high charge density of ions causes them to attract (and retain) solvent molecules by ion–dipole coupling. This phenomenon, known as solvation, powerfully inhibits the translational and rotational motions of solvent molecules and hence lowers their entropy. Secondly, at high concentrations, ions lose their mutual independence because their electric fields penetrate far into solution. Indeed, the electrostatic potential energy of a pair of point charges varies as r ⁻¹, which is very long range indeed. (Compare the potential energy of the van der Waals interaction, which varies as r ⁻⁶.) By having such a long-range influence, an ion is typically able to interact with a large population of mobile counterions and co-ions in its vicinity. This population is known as its “ionic atmosphere.” Though fluctuating continually in structure and composition, the ionic atmosphere has a time-averaged charge opposite to that of the central ion and is therefore electrically attracted to it.

Actually, the time-averaged charge on the ionic atmosphere necessarily balances the charge on the central ion because of the principle of electroneutrality. If we denote the valence of the ith type of ion by z _i and all the ions are mobile, then in the absence of an externally applied electric field we have

$$ \sum\limits_i {{c_i}{z_i}} = 0 $$

(3.1)

where c _i is the time-averaged number of i-ions per unit volume. Thus, the charge on the central ion, plus the time-averaged charge on the ionic atmosphere, equals 0.

Debye–Hückel theory

Historically, the thermodynamics of nonideal solutions appeared to be an intractable problem until the seminal work of Peter Debye and Erich Hückel in the 1920s [27, 28]. In 1923, they succeeded in develo** a mathematical model of ionic solutions which included long-range electrostatic interactions, although they still assumed a continuum model of the solvent. In their mind’s eye, they placed one particular ion at the origin of a spherical coordinate system and then investigated the time-average distribution of electric potential ϕ (phi) surrounding it. Instead of the expected Coulomb potential,

$$ \varphi (r) = \frac{Q}{{4\pi {\varepsilon_0}{\varepsilon_{\rm{r}}}\,r}} $$

(3.2)

they found the screened Coulomb potential,

$$ \varphi (r) = \frac{Q}{{4\pi {\varepsilon_0}{\varepsilon_{\rm{r}}}\,r}}\,\exp \,\left( { - \frac{r}{{{r_{\rm{D}}}}}} \right) $$

(3.3)

Here, Q is the charge on the central ion; ε ₀ (epsilon) is the permittivity of free space; ε _r is the relative permittivity (dielectric constant) of the solution; r is the distance from the central ion; and r _D is a constant. Since the exponential function has a value less than 1, the effect of long-range electrostatic interactions between ions is always to diminish the electric potential of the central ion and, by extension, to diminish the electric potential of every ion in solution. The magnitude of this “screening effect” is determined by the parameter r _D, where

$$ {r_{\rm{D}}} = \sqrt {{\frac{{{\varepsilon_0}{\varepsilon_{\rm{r}}}{k_{\rm{B}}}T}}{{2{N_{\rm{A}}}{e^2}\mu }}}} $$

(3.4)

and

$$ \mu = \frac{1}{2}\,\sum {{c_i}z_i^2} $$

(3.5)

Here, k _B is the Boltzmann constant; N _A is the Avogadro number; e is the elementary charge; μ (mu) is the ionic strength of the solution (M); c _i is the molar concentration of the ith type of ion; z _i is the valence of the ith type of ion; and the sum is taken over all the ions in solution. The parameter r _D has the dimensions of length and is widely known as the Debye length. It is noteworthy that the Debye length is inversely proportional to the square root of the ionic strength, which is an experimental variable.

The significance of the Debye length r _D is that it measures the radius of the ionic atmosphere surrounding the central ion. It also indicates the scale of length below which fluctuations from electroneutrality are significant and above which they are insignificant. Finally, the Debye length also determines the distance of closest approach of two similarly charged ions in solution, since they cannot approach within 2r _D of each other without feeling strong electrostatic repulsion.

Remark

As the ionic strength μ is increased, ions of the same polarity may approach each other more closely and thereby increase the probability of electron tunneling between them.

Overall, the picture that emerges from Debye–Hückel theory is that every ion in solution is surrounded by a supermolecular arrangement of counterions and co-ions. The time-averaged charge on this “supermolecule” (= central ion plus ionic atmosphere) is necessarily 0. However, the instantaneous charge may be positive or negative, depending on whether there is a transient excess of cations or anions.

As far as electron transfer theory is concerned, the fact that the time-averaged charge on each supermolecule is 0 has some very important consequences. Consider, for example, an iron (3+) ion surrounded, on average, by three mobile chloride ions. If the iron (3+) ion takes part in an electron transfer process and receives an electron, then it ends up as an iron (2+) ion, and so its ionic atmosphere must adjust by expelling a surplus chloride ion. In a similar way, if an iron (2+) ion loses an electron, then it ends up as an iron (3+) ion, and at some stage its ionic atmosphere must adjust by attracting an extra chloride ion. These charge-compensating events are an intrinsic part of electron transfer in electrolyte solutions, and the energy associated with them must be included in any theory.

Remark

In the presence of mobile ions, every electron transfer event is charge-compensated by an ion transfer event. This is an elementary consequence of the principle of electroneutrality.

Solvation

Although Debye–Hückel theory is successful in quantifying electrostatic interactions at long range, it still fails badly at short range. In particular, it fails to account for solvation and its many side effects. Quite commonly, solvent molecules that are immediately adjacent to ions lose some of their translational and rotational entropy; their dielectric response becomes saturated; and their molar volume is compressed below normal. None of these effects is captured by classic Debye–Hückel theory.

If the solvent is water, then solvation is referred to as hydration. Formally, the hydration process may be represented as

$$ {{\hbox{M}}^{q + }} + n{{\hbox{H}}_2}{\hbox{O}} \leftrightarrows {\left[ {{\hbox{M}}{{\left( {{{\hbox{H}}_2}{\hbox{O}}} \right)}_n}} \right]^{q{ + }}} $$

(3.6)

The values of the Gibbs energy, enthalpy, and entropy of hydration of some main group cations are collected in Table 3. The entropy loss due to the binding of a single water molecule is about −28 J K⁻¹ mol⁻¹ at 298 K. Thus, dividing each entropy of hydration in Table 3 by −28 J K⁻¹ mol⁻¹ yields a “thermodynamic hydration number” n. This parameter gives a useful indication of the time-averaged number of water molecules actually bonded to each ion. Of course, other water molecules are also nearby, but they are less strongly bonded. From the final column of Table 3, we readily see that singly charged cations are weakly hydrated, while multiply charged cations are strongly hydrated.

Table 3 Values of the Gibbs energy, enthalpy, and entropy of hydration of some common cations in water at 298.15 K and 1-atm pressure

If electron transfer changes the size of an ion (as it often does), then it follows that some energy must be supplied to expand or contract the associated solvation shell. This idea was first suggested by John Randles in 1952, and it led to the first successful kinetic theory of electron transfer based on molecular properties [33].

Things get even more complicated when we look at transition metal cations. Solutions of these species typically consist of coordination complexes (central metal ions with ligands attached) and mobile counterions to preserve electroneutrality. The structural principles of coordination complexes were largely understood by 1913, when Alfred Werner was awarded the Nobel Prize in Chemistry for his work in this area [34]. In a virtuoso performance, Werner had shown that the structure of the compound CoCl₃⋅6NH₃ was actually [Co(NH₃)₆]Cl₃, with the Co(3+) ion surrounded by six NH₃ ligands at the vertices of an octahedron. The NH₃ ligands constituted an “inner” coordination shell, with the three chloride ions constituting an “outer” solvation shell in the form of an ionic atmosphere. Werner had also analyzed analogous complexes containing bidentate ligands, most notably tris(ethylenediamine) cobalt (III) chloride, [Co(en)₃]Cl₃.

Outer-sphere and inner-sphere kinetics

Despite Werner’s success in establishing the structural principles of coordination complexes, the kinetic principles resisted analysis until much later, mainly because of the complicated mixtures of ligand substitution and electron tunneling that were involved. Indeed, progress was stalled until after World War II, when radioactive tracers such as ⁶⁰Co and ³⁶Cl became available from cyclotrons in the USA. In 1949, an epoch-making paper [35] was published by W.B. Lewis, Charles DuBois Coryell, and John W. Irvine, Jr., on the mechanism of electron transfer between the tris(ethylenediamine) complex of Co²⁺ and the corresponding complex of Co³⁺,

$$ {\left[ {{\hbox{*Co}}{{\left( {\hbox{en}} \right)}_3}} \right]^{{2} + }} \cdot {\hbox{2C}}{{\hbox{l}}^{-} } + {\left[ {{\hbox{Co}}{{\left( {\hbox{en}} \right)}_3}} \right]^{{3} + }} \cdot {\hbox{3C}}{{\hbox{l}}^{-} } \to {\left[ {{\hbox{*Co}}{{\left( {\hbox{en}} \right)}_3}} \right]^{{3} + }} \cdot {\hbox{3C}}{{\hbox{l}}^{-} } + {\left[ {{\hbox{Co}}{{\left( {\hbox{en}} \right)}_3}} \right]^{{2} + }} \cdot {\hbox{2C}}{{\hbox{l}}^{-} } $$

(3.7)

Here, en = NH₂⋅CH₂⋅CH₂⋅NH₂. By using a radioactive tracer (⁶⁰Co), these authors showed that, in this special case, ligand substitution was entirely absent. The ethylenediamine ligands remained firmly bound to the metal centers throughout the course of the reaction, thus proving that electron transfer could occur without any interpenetration of the inner solvation shells of the two reactants. Almost incredibly (or so it seemed at the time), the electron was tunneling from one complex to the other without bond making or bond breaking. It was the first example of what was later to be called an outer-sphere electron transfer process. Today, we know that electrons can tunnel as much as 1.4 nm through free space and even further if intervening species (such as water molecules or ligands) provide conduit electronic states.

Definition

An electron transfer process between two transition metal complexes is classified as outer sphere if the charge-compensating ion transfer process does not penetrate the inner coordination shell of either reactant.

Remark

This definition of outer-sphere electron transfer does not exclude the possibility that the inner coordination shells of both reactants might be elastically distorted during the reaction.

A few years later, in 1953, Henry Taube, Howard Myers, and Ronald L. Rich discovered a counterexample to outer-sphere electron transfer, involving electron transfer from the hexa(aquo) complex of Cr^II to the chlorido penta(amino) complex of Co^III [36, 37]. This reaction can be written

$$ {\left[ {{\hbox{C}}{{\hbox{r}}^{\rm{II}}}{{\left( {{{\hbox{H}}_2}{\hbox{O}}} \right)}_6}} \right]^{{2} + }} \cdot {2}{{\hbox{P}}^{-} } + {\left[ {{\hbox{C}}{{\hbox{o}}^{\rm{III}}}{{\left( {{\hbox{N}}{{\hbox{H}}_3}} \right)}_5}{\hbox{*Cl}}} \right]^{{2} + }} \cdot {2}{{\hbox{P}}^{-} } \to {\left[ {{\hbox{C}}{{\hbox{r}}^{\rm{III}}}{{\left( {{{\hbox{H}}_2}{\hbox{O}}} \right)}_5}{\hbox{*Cl}}} \right]^{{2} + }} \cdot {2}{{\hbox{P}}^{-} } + {\left[ {{\hbox{C}}{{\hbox{o}}^{\rm{II}}}{{\left( {{\hbox{N}}{{\hbox{H}}_3}} \right)}_5}{{\hbox{H}}_2}{\hbox{O}}} \right]^{{2} + }} \cdot {2}{{\hbox{P}}^{-} } $$

(3.8)

where (P⁻) is the perchlorate counterion. By a combination of spectrophotometry and radioactive tracer studies, the authors deduced that the radioactive *Cl⁻ ion was acting as a bridging ligand between the chromium and cobalt metal centers while the electron transfer occurred (Fig. 4). Furthermore, a negligible amount of free *Cl⁻ was found in solution at the end of the reaction. This was the first example of an inner-sphere (bridged) electron transfer process. Soon afterwards, numerous other complexes of the type [Co^III(NH₃)₅ L]²⁺⋅2X⁻ were synthesized, such as L = F⁻, Br⁻, I⁻, CNS⁻, N ⁻₃ , and these were all found to behave in a similar way [38].

Fig. 4

Schematic diagram of the inner-sphere (bridged) transition state discovered by Taube et al. [36, 37]

Definition

An electron transfer process between two transition metal complexes is classified as inner sphere if the charge-compensating ion transfer process penetrates the inner coordination shell of either reactant.

Since the discoveries of Lewis et al. and Taube et al., a vast literature has accumulated on the mechanisms and kinetics of outer-sphere and inner-sphere electron transfer reactions. It is particularly interesting to compare the rate constants of well-attested examples. Some of these are shown in Table 4. It can be seen that both types of reaction may be “fast” (k _et > 10³ L mol⁻¹ s⁻¹), and both types of reaction may be “slow” (k _et < 10⁻³ L mol⁻¹ s⁻¹), with the observed rate constants spanning more than six orders of magnitude in each category. Even from this small set of data, it is obvious that the rates of electron transfer reactions are extremely sensitive to small differences in molecular structure.

Table 4 Selected second-order rate constants for inner-sphere and outer-sphere electron transfer reactions in water

How exactly do small differences in molecular structure exert such a profound effect on the rates of electron transfer reactions? Thermodynamics provides some clues. It tells us that, in order to reach the transition state, elastic distortions of the complexes may be required or charge fluctuations within the Debye radius of the central ion or both. Thus, the elastic moduli of the molecules and the local distribution of electrical charges must both be considered. Once the transition state has been reached, quantum mechanical criteria also come into play. The donor and acceptor orbitals must overlap in order for efficient electron tunneling to occur, and the orbital symmetries must coincide (i.e., constructive interference must occur between the wave functions, not destructive interference). Finally, the chemical identity of the bridging ligand is a further consideration. Each ligand generates a different lifetime of the transition state, and this also affects the probability of electron transfer. In all these various ways, the structures of transition metal complexes may influence the rates of electron transfer.

Research during the 1950s initially found that the vast majority of electron transfer reactions were inner-sphere type. The explanation for this bias lay in the electronic structure of the ligands that were being used. At that time, there was a particular focus on anionic ligands, and most of them had lone pairs of electrons that were arranged at 180° to each other, which meant they were readily able to bridge the metal centers in the transition state. Examples included F⁻, Cl⁻, Br⁻, I⁻, CNS⁻, N ⁻₃ , CN⁻, SCN⁻, and ONO⁻. Among the few exceptions were H₂O and NH₃. Later, the use of neutral organic ligands whose lone pairs of electrons were all directed inwards towards the central ion (such as 1,10-phenanthroline, ethylenediamine, 2,2′-bipyridine, and 2,2′:6′,2″-terpyridine) began to reverse the trend, and examples of outer-sphere electron transfer also began to accumulate.

By the 1960s, however, experimentalists had realized that all the known inner-sphere and outer-sphere electron transfer reactions had multiple sensitivities to different aspects of molecular structure, and this prompted them to search for kinetically simpler instances of both cases. In the case of inner-sphere electron transfer reactions, a particularly vexing problem was the short lifetime of the bridged intermediates, which made them very difficult to study. So a search began for stable bridge linkages that would allow spectroscopic measurements on the timescale of seconds. The triumphant result was the synthesis of μ-pyrazine-bis(pentaammineruthenium)(II,II) tosylate by Peter Ford at Stanford in 1967 [43]. This has the formula [(NH₃)₅Ru(μ-pyz)Ru(NH₃)₅]⁴⁺[(Ts)₄]^4–, and it was soon oxidized by Carol Creutz and Henry Taube [44] to make the mixed-valent (II,III) ion shown in Fig. 5 (the Creutz–Taube ion). This latter has subsequently become the exemplar of all mixed-valent compounds [45]. The synthesis of the Creutz–Taube ion also made it possible to study electron transfer at fixed separation of the donor and acceptor states, a feat which eliminated the encounter distance as an experimental variable.

Fig. 5

Schematic diagram of the μ-pyrazine-bis(pentaammineruthenium)(II,III) complex (The Creutz–Taube ion)

In the case of outer-sphere reactions, the revised goal was a redox couple that would not need any elastic distortions in its inner coordination shell in order to convert from reactants to products. After some effort, it was found that the tris(2,2′-bipyridyl)ruthenium complexes Ru(bpy) ²⁺₃ and Ru(bpy) ³⁺₃ had identical octahedral geometries within experimental error (Ru-N distances = 0.2055 ± 0.0005 nm in both cases) [46]. As expected, this couple exhibited a phenomenally fast second-order rate constant in aqueous perchloric acid solution, namely 2 × 10⁹ L mol⁻¹ s⁻¹ (almost diffusion-controlled) [47]. Furthermore, the entropy of reaction was 0 [48, 49]. As a result of these special features, the tris(2,2′-bipyridyl)ruthenium (II/III) reaction gradually became the paradigm of outer-sphere electron transfer reactions, and it still holds that special status today (Fig. 6).

Fig. 6

Schematic diagram of the tris(2,2′-bipyridyl)ruthenium complex, the paradigm of outer-sphere electron transfer reactions

Effects of ionic strength

Despite many careful kinetic studies and the synthesis of innumerable transition metal complexes, one area of research that was comparatively neglected during the 1950s and 1960s was the effect of the ionic strength of solution on the rates of outer-sphere electron transfer processes. In 1982, however, an important paper was published by Harald Bruhn, Santosh Nigam, and Josef F. Holzwarth [50].

These authors investigated outer-sphere electron transfer processes between pairs of highly negatively charged complexes at different ionic strengths of solution. In particular, they determined the second-order rate constants for the reduction of hexachloroiridium(IV) by meso-tetraphenylporphyrin-tetrasulfonate silver(II),

$$ {\left[ {{{\left( {\hbox{M}} \right)}_2}} \right]^{{2} + }}{\left[ {{\hbox{I}}{{\hbox{r}}^{\rm{IV}}}{{\left( {\hbox{Cl}} \right)}_6}} \right]^{{2} - }} + {\left[ {{{\left( {\hbox{M}} \right)}_4}} \right]^{{4} + }}{\left[ {{\hbox{A}}{{\hbox{g}}^{\rm{II}}}\left( {\hbox{TPPTS}} \right)} \right]^{{4} - }} \to {\left[ {{{\left( {\hbox{M}} \right)}_3}} \right]^{3 + }}{\left[ {{\hbox{I}}{{\hbox{r}}^{\rm{III}}}{{\left( {\hbox{Cl}} \right)}_6}} \right]^{3 - }} + {\left[ {{{\left( {\hbox{M}} \right)}_3}} \right]^{3 + }}{\left[ {{\hbox{A}}{{\hbox{g}}^{\rm{III}}}\left( {\hbox{TPPTS}} \right)} \right]^{3 - }} $$

(3.8)

where M⁺ = Li⁺, Na⁺, K⁺, and Cs⁺. Some of their data are plotted in Fig. 7. The results demonstrate the effect of changing the ionic strength of the supporting electrolyte (M⁺Cl⁻). At low ionic strength (μ < 0.5 M), electron transfer takes place through the diffuse layers of both complexes, and since the probability of electron transfer declines steeply with increasing separation, the reaction “switches off.” But at high ionic strength (μ > 0.5 M), the diffuse layer collapses to near-zero thickness, and the rate of electron transfer saturates.

Fig. 7

Influence of ionic strength μ on the second-order rate constant k _et for electron transfer between two strongly negatively charged species in aqueous solution. Data from H. Bruhn et al. [50]

One way to picture the effect of ionic strength is to imagine that the solution is composed of neutral ionic clusters (supermolecules), Fig. 8. Embedded inside each supermolecule is a reactant ion surrounded by its ionic atmosphere. As the ionic strength changes, so too does the thickness of the ionic atmosphere, according to the relation ${r_{\rm{D}}} \propto \sqrt {{{1 \mathord{\left/{\vphantom {1 \mu }} \right.} \mu }}}$ (Eq. 3.4).

Fig. 8

The concept of a supermolecule (=ion + ionic atmosphere)

In summary, the supporting electrolyte plays two important roles in solution-phase electron transfer. Firstly, it provides long-range screening of electrically charged species, allowing them to approach each other without doing electrostatic work. Secondly, when the species are within electron tunneling distance, it provides the charge fluctuations that cause the electrostatic potentials of the donor and acceptor species to equalize, thus ensuring that the electron transfer takes place with conservation of energy.

Molecular models of electron transfer

In previous sections, we showed that if equilibrium fluctuations trigger electron transfer, then the activation energy can be expressed in the generic form

$$ \Delta G_{\rm{RC}}^{*} = \int_0^{{L^*}} {f\,{\hbox{d}}L} + \int_0^{{Q^*}} {\varphi \,{\hbox{d}}Q} $$

(4.1)

where $\Delta G_{\rm{RC}}^{*}$ is the Gibbs energy of activation; f is mechanical force; L is extension; ϕ is electric potential; and Q is charge. We also showed that the two terms on the right-hand side of this equation correspond to two fundamentally different types of activation process, namely (1) elastic distortions of the donor and acceptor species, which take place against their internal force fields, and (2) charge fluctuations within the Debye radius of the donor and acceptor species, which take place against the self-repulsions of the charges. In what follows, we describe molecular models of both of these processes. The elastic distortion model was elaborated by John Randles in 1952 [33], building on some prewar work of Meredith Evans [51]. The charge fluctuation model was proposed by Stephen Fletcher in 2007 [22]. A third model, which assumes that nonequilibrium fluctuations of solvent molecules trigger electron transfer, was proposed by Rudolph Marcus in 1956 [52–55] and will be discussed separately later.

The elastic distortion model

The principal features of the elastic distortion model are sketched in Fig. 9, using the aqueous Fe(II)/Fe(III) couple as an example. The Morse-type curves represent the potential energies of the inner solvation shells of the ferrous and ferric ions as a function of their radii. These potential energies were considered by Randles to be the main contributors to the Gibbs energy of activation of electron transfer. Here, for ease of exposition, we focus on the half-reaction

$$ {\left[ {{\hbox{F}}{{\hbox{e}}^{\rm{III}}}{{\left( {{{\hbox{H}}_2}{\hbox{O}}} \right)}_6}} \right]^{{3} + }} + {{\hbox{e}}^{-} }\,\,\, \to \,\,\,{\left[ {{\hbox{F}}{{\hbox{e}}^{\rm{II}}}{{\left( {{{\hbox{H}}_2}{\hbox{O}}} \right)}_6}} \right]^{{2} + }} $$

(4.2)

at an electrode surface and ignore the reverse reaction.

Fig. 9

Potential energies of the inner solvation shells of ${\hbox{F}}{{\hbox{e}}^{\rm{II}}}{\left( {{{\hbox{H}}_2}{\hbox{O}}} \right)_6}$ and ${\hbox{F}}{{\hbox{e}}^{\rm{III}}}{\left( {{{\hbox{H}}_2}{\hbox{O}}} \right)_6}$ complexes as a function of their radii. From J.E.B. Randles [33]. The energy of the lowest vibrational state of Fe(II) is arbitrarily assigned a value of 0

Since the radii of the inner solvation shells of the ferrous and ferric ions are not identical, it is obvious that some change in radius must take place during electron transfer. But at what stage? Randles’ brilliant insight was that “In accordance with the Franck–Condon principle the electron transfer will correspond to a vertical transition between the curves and it is clear that the reaction must proceed over the energy barrier pqr with the electron transfer occurring at q.” In other words, what Randles proposed was that some fraction of the change in radius takes place before the electron transfer, and some fraction takes place after, with the precise ratio determined by the location of the intersection point on the potential energy curves.

At the intersection point q (the transition state), the inner solvation shells of the Fe(II) and Fe(III) ions have equal radii. Thus, on the Randles model, the activation energy of electron transfer is just the work required to change the radius (bond length) of the inner solvation shell from its lowest vibrational-state value to its transition-state value.

Remark

The Randles approach is clearly not valid for electron transfer to more complex molecules, such as redox proteins, because it neglects distortions of bond angles and distortions of torsion angles. However, if desired, it could readily be extended to include such cases.

A well-known method of calculating the Randles activation energy is the following [56]. At room temperature, all molecules exhibit multiple vibrations, which have a strong tendency to synchronize with each other, forming what are known as normal modes of vibration. In normal modes, all the atoms vibrate with the same frequency and phase. One of the normal modes, known as the spherically symmetric normal mode, is of special interest because it describes the radial in-and-out motion of the entire first solvation shell. By focusing on this mode and excluding all other modes, it becomes possible to determine the precise amount of energy needed to expand or contract the first solvation shell up to its transition-state size.

The beauty of the normal mode analysis is that it allows theorists to ignore all the complicated energy changes of individual ligands—which would normally require a multitude of reaction coordinates—and replace them with a single measure (the energy of extension) which requires only a single reaction coordinate (the radius of the inner solvation shell). A further advantage of the analysis is that the spherically symmetric normal mode is a very loose mode, having energy levels so close together that they effectively form a continuum. This allows the Randles activation energy to be derived without recourse to quantum mechanics. Indeed, the chemical bonds that connect the central ion to its solvation shell can be treated as a single, classical spring that continually exchanges energy with the surrounding solution.

From Eq. 4.1, in the absence of charge fluctuations, we have

$$ \Delta G_{\rm{RC}}^{*} \approx \int_0^{{L^*}} {f\,{\hbox{d}}L} $$

(4.3)

where f is force and L is extension. And from Hooke’s law (“As the extension, so the force...”), we may assume the linear response relation

$$ f = - kL $$

(4.4)

where k is the spring constant. The negative sign merely indicates that the force opposes the extension.

Remark

Because the physical stretching of chemical bonds always exhibits nonlinear behavior at high force, one must not push the linear response relation too far.

Assuming the linear response relation is applicable, the Gibbs energy that must be supplied to expand or contract the inner solvation shell is

$$ \Delta G_{\rm{RC}}^{*} \approx \int_0^{{L^*}} {kL\,{\hbox{d}}L} $$

(4.5)

$$ \Delta G_{\rm{RC}}^{*} \approx \frac{{kL{*^2}}}{2} $$

(4.6)

In the scientific literature, Eq. 4.6 is widely known as the “harmonic oscillator approximation” or simply the “harmonic approximation.” This is a confusing terminology, however. For while it is true that Morse-type potential energy curves are tolerably well approximated by parabolas and the system would indeed perform simple harmonic motion if it were isolated, the fact is that the system is not isolated—it continually exchanges energy with the bulk of solution—and so the amplitude of the spherically symmetric normal mode actually varies randomly in time. As a result, the atoms of the solvation shell are executing motions considerably more complex than those of simple harmonic motion.

By noting that the extension required to reach the transition state is

$$ L* = r* - {r_0} $$

(4.7)

where r* is the transition-state radius of the inner solvation shell and r ₀ is the ground-state radius of the inner solvation shell, we finally arrive at the textbook formula for the activation energy on the Randles model,

$$ \Delta G_{\rm{RC}}^{*} \approx \frac{{k{{\left( {r* - {r_0}} \right)}^2}}}{2} $$

(4.8)

This is highly satisfactory. The radius of the inner solvation shell of the ion acts as the reaction coordinate, and the transition state occurs at the point on the reaction coordinate where the Gibbs energy curves of the donor and acceptor species intersect. Most important of all, this elegant arrangement also guarantees that the Franck–Condon principle and the conservation of energy are satisfied simultaneously.

In passing, we note that the Randles activation energy can also be written in the form

$$ \Delta G_{\rm{RC}}^{*} \approx \frac{{{{\left( {{\lambda_{\rm{inner}}} + \Delta {G^0}} \right)}^2}}}{{4{\lambda_{\rm{inner}}}}} $$

(4.9)

where λ _inner is the “reorganization energy” of the inner solvation shell and ∆G ⁰ is the difference in Gibbs energy between the unfluctuated donor and the unfluctuated acceptor states (i.e., the driving force for the reaction.) In electron transfer theory, the parameter λ _inner is a hypothetical quantity, equal to the energy that would be required to give the reactant the inner solvation shell of the product, without electron transfer. A formula of this type was first published by Ryogo Kubo and Yutaka Toyozawa in 1955 [57]. In more recent times, the total reorganization energy λ of an electrochemical system has been written as the sum of an inner contribution λ _inner and an outer contribution λ _outer, attributed to the complete reorganizations of the redox partners and their environment.

The charge fluctuation model

The successful development of the elastic distortion model by John Randles was a major milestone in the history of solution-phase electron transfer. However, almost as soon as it was published, the question arose as to what was determining the activation energy of electron transfer in cases where the inner solvation shell was not elastically distorted or was distorted only slightly. In various guises, this question has haunted electron transfer theory ever since. Clearly, some process occurs in the outer solvation shell that is able to trigger electron transfer. But what is it?

In 2007, it was suggested by Fletcher that the mysterious process might be the Brownian motion of co-ions and counterions into and out of the ionic atmospheres of the reactants [22]. Such a process—which would occur even at thermodynamic equilibrium—would cause charge fluctuations inside the ionic atmospheres of the donor and acceptor species, which in turn would drive the system towards the transition state for electron transfer. This explanation has many attractive features, including full compatibility with the Franck–Condon principle, the Debye–Hückel theory, and the equipartition of energy.

The charge fluctuation model is based on the following assumptions [22]:

• 1. There is an ionic atmosphere of co-ions and counterions, so Debye–Hückel screening is present.

• 2. The charges on the reactant species are fully screened outside the Debye length.

• 3. Fluctuations of electrostatic potential are generated inside the Debye length by the Brownian motion of co-ions and counterions.

In the original paper, the central results were obtained by develo** an “equivalent circuit” model of the reactant supermolecules. (Recall that a supermolecule is just an ion plus its ionic atmosphere.) Here, we derive the same results in a more elementary way, from Eq. 4.1, in order to illustrate the similarities and differences with the Randles model. Just as we did in the case of the Randles model, we focus on the half-reaction of Eq. 4.2 and ignore the reverse reaction.

From Eq. 4.1, in the absence of elastic distortions, we have

$$ \Delta G_{\rm{RC}}^{*} \approx \int_0^{{Q^*}} {\varphi \,{\hbox{d}}Q} $$

(4.10)

where ϕ is electrostatic potential, and Q is charge. Once again, we assume a linear response relation, explicitly

$$ \varphi = \Lambda Q $$

(4.11)

where the coefficient Λ (lambda, a constant) is the electrical elastance (farad⁻¹) of the ionic atmosphere. Note that this relation is just the electrical analog of Hooke’s law. Accordingly, the work that must be supplied to concentrate the charge on the ionic atmosphere of the donor or acceptor in the transition state is

$$ \Delta G_{\rm{RC}}^{*} \approx \int_0^{{Q^*}} {\Lambda Q\,{\hbox{d}}Q} $$

(4.12)

$$ \Delta G_{\rm{RC}}^{*} \approx \frac{{\Lambda Q{*^2}}}{2} $$

(4.13)

Alternatively, writing the elastance Λ as the reciprocal capacitance 1/C, we have

$$ \Delta G_{\rm{RC}}^{*} \approx \frac{{Q{*^2}}}{{2C}} $$

(4.14)

This formula will of course be familiar to electrical engineers—it is just the work required to charge a conducting sphere in a dielectric medium. This suggests that we might justifiably model a supermolecule (ion + ionic atmosphere) as a conducting sphere in a dielectric medium. Let us do that here. Since the capacitance of a conducting sphere is

$$ C = 4\pi {\varepsilon_0}{\varepsilon_{\rm{r}}}\left( \omega \right)a $$

(4.15)

where ε ₀ (epsilon) is the permittivity of free space, ε _r(ω) is the relative permittivity (dielectric constant) of the solution as a function of frequency ω (omega), and a is the radius of the sphere, it follows immediately that the Gibbs energy of activation is

$$ \Delta G_{\rm{RC}}^{*} \approx \frac{1}{2}Q{*^2}\left( {\frac{1}{{4\pi {\varepsilon_0}{\varepsilon_{\rm{r}}}\left( \omega \right)a}}} \right) $$

(4.16)

Remark

The radius of the supermolecule consists of three main contributions: the radius of the central ion, the thickness of the inner solvation shell, and the thickness of the diffuse layer. Through the latter, the radius a depends on the ionic strength of solution.

At this point, a new problem must be confronted. Since the relative permittivity (dielectric constant) of the solution depends on the frequency ω at which it is perturbed (or, equivalently, depends on the time scale ω ⁻¹ over which the perturbation is applied), it is necessary to decide which value of ω is appropriate to our problem. A reasonable estimate can be obtained from the Franck–Condon principle, which tells us that molecules possess so much inertia that they cannot move during the elementary act of electron tunneling. This implies that the only part of the relative permittivity that can respond is the electronic part (i.e., the high-frequency component), viz.

$$ \varepsilon \left( \omega \right) \approx \varepsilon \left( \infty \right) $$

(4.17)

So we finally obtain

$$ \Delta G_{\rm{RC}}^{*} \approx \frac{1}{2}Q{*^2}\left( {\frac{1}{{4\pi {\varepsilon_0}{\varepsilon_{\rm{r}}}\left( \infty \right)a}}} \right) $$

(4.18)

where Q* is the transition-state value of the charge fluctuation. Just as we found in the Randles model, the transition state occurs at the point where the Gibbs energy curves of the donor and acceptor species intersect. Unlike the Randles model, however, the reaction coordinate is now the electrical charge on the supermolecule rather than the mechanical extension of the ligands.

Interestingly, since the mechanical extension and the electrical charge are independent degrees of freedom of the system, the total activation energy may be decomposed into two terms:

$$ \Delta G_{\rm{RC}}^{*} \approx \frac{{k{{\left( {r* - {r_0}} \right)}^2}}}{2} + \frac{{\Lambda Q{*^2}}}{2} $$

(4.19)

However, identification of the dominant term in any given system must be a matter of empirical enquiry.

For the charge fluctuation model, the results for one supermolecule can readily be extended to the case of electron transfer between two supermolecules, D and A, where D is an electron donor and A is an electron acceptor [22]. The goal in this case is a formula for the activation energy of two charge fluctuations of identical magnitude but opposite sign, one on each supermolecule. The result is

$$ \Delta G_{\rm{RC}}^{*} = \frac{1}{2}Q{*^2}\,\left( {\frac{1}{{4\pi {\varepsilon_0}}}} \right)\,\,\left( {\frac{1}{{{\varepsilon_{\rm{r}}}\left( \infty \right)}}} \right)\,\,\left( {\frac{1}{{{a_{\rm{D}}}}} + \frac{1}{{{a_{\rm{A}}}}}} \right) $$

(4.20)

where a _D is the radius of the donor supermolecule, and a _A is the radius of the acceptor supermolecule. Under normal conditions, the charge fluctuation on the donor is fractionally negative, and the charge fluctuation on the acceptor is fractionally positive, and these reverse polarity at the moment of electron transfer.

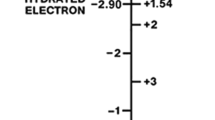
The charge fluctuation theory has also been extended to highly exergonic reactions (the “inverted region”) and to highly endergonic reactions (the “superverted region”), as shown in Fig. 10 [58]. The principal results are: (1) In the inverted region, the donor supermolecule remains positively charged both before and after the electron transfer event. (2) In the normal region, the donor supermolecule changes polarity from negative to positive during the electron transfer event. (3) In the superverted region, the donor supermolecule remains negatively charged both before and after the electron transfer event [58]. This overall pattern of events makes it possible for polar solvents to catalyze electron transfer in the inverted and superverted regions by screening the charge fluctuations on the supermolecules—a completely new type of chemical catalysis.

Fig. 10

Schematic diagram showing how the rate constants for electron transfer (k _et) vary with driving force (−ΔG ⁰) and reorganization energy (λ) on the theory of charge fluctuations [58]

In the normal region, where the vast preponderance of experimental data has been obtained, solvent molecules outside the supermolecules are not preferentially orientated in the transition state. If they were, they would have to reverse their orientation at the moment of electron transfer, and that process would violate the Franck–Condon principle. On the other hand, solvent molecules inside the supermolecules do become attached to the charge fluctuations by ion–dipole coupling and thereby lose rotational and translational entropy. This means that, on the charge fluctuation model, the entropy of activation of electron transfer is necessarily negative. Due to electrostriction, the volume of activation must likewise be negative.

The solvent fluctuation model

So far, we have discussed the theory of electron transfer from the viewpoint of processes that occur at equilibrium or close to equilibrium. Now, we broaden our horizons to include processes that occur far from equilibrium. Explicitly, we consider the solvent fluctuation model [52, 53]. Since its introduction by Rudolph A. Marcus in the mid-1950s, this model has enjoyed a tremendous vogue, and today it represents the most widely accepted theory of electron transfer in the world.

The solvent fluctuation model is based on the following assumptions [54, 55]:

• 1. The ionic atmosphere of co-ions and counterions can be neglected, so Debye–Hückel screening is absent.

• 2. The bare charges on the reactant species are screened only by solvent molecules.

• 3. Fluctuations of electrostatic potential are generated by the ordering/disordering of solvent dipoles near the reactant molecules.

Marcus used a continuum dielectric model for the solvent, rather than a molecular model, which led to a number of compact formulas for electron transfer between ions (but which also made his reaction coordinate difficult to understand). He also used the same formalism to model electron transfer between ions and electrodes. However, due to the unscreened nature of the bare charges on the reactant species, he was compelled to introduce work terms for bringing the reactants together and separating the products, something that is not needed in concentrated solutions of supporting electrolytes.

On the Marcus model, the transition state for electron transfer is created by solvent fluctuations. In the normal region of electron transfer, for a self-exchange reaction, the idea is that the less-charged species becomes more solvated, and the more-charged species becomes less solvated, so that the solvation shells of both species come to resemble each other. The net effect is a rough cancelation of any entropy changes in forming the transition state. This contrasts markedly with the charge fluctuation model, which predicts that the entropy of activation of electron transfer should always be negative.

Unfortunately for the Marcus model, there is no well-attested evidence that the entropies of activation of simple self-exchange electron transfer reactions are close to 0. There is, however, a great deal of evidence that the entropies of activation are substantially negative. Some examples are given in Table 5. Where high-pressure data are available, as in Table 6, the volumes of activation of electron transfer are also negative, implying the existence of electrostriction in the transition states. In summary, both categories of data suggest that the process of electron transfer in solution involves an increase in charge in the transition state.

Table 5 Entropies of activation (ΔS*) of some self-exchange reactions

Table 6 Volumes of activation (ΔV*) of some self-exchange reactions

Kinetic evidence in favor of the Marcus model is also lacking. For example, the solvent fluctuation theory predicts that the rate constant for electron transfer should be greater in less polar solvents, and that has never been observed (Fig. 11). In addition, the solvent fluctuation theory predicts that the graph of rate constant for electron transfer versus driving force should be symmetric (an inverted parabola), and that has never been observed either. Given all these difficulties, it may be timely to reconsider whether fluctuations of solvent dipoles really are the principal cause of electron transfer in electrolyte solutions.

Fig. 11

Schematic diagram showing how the rate constants for electron transfer (k _et) vary with driving force (−ΔG ⁰) and reorganization energy (λ) on the Marcus model, for solvents of different polarity

The inverted region

The experimental observation of an inverted region (i.e., a range of driving forces in which the rate constant for electron transfer actually decreases as the driving force increases) has been among the most remarkable discoveries in modern chemical science. The phenomenon itself is strongly counterintuitive, and its existence places powerful constraints on any prospective theory of electron transfer. Thus, among the models of electron transfer discussed in this article (Randles, Fletcher, Marcus), all of them predict the existence of an inverted region, although only the charge fluctuation model of Fletcher predicts an asymmetric response without the introduction of ad hoc hypotheses.

Rudolph A. Marcus noted as early as 1960 that his model of electron transfer might be applied to the topic of “inverted” behavior [67], but it took another 20 years before inverted behavior was actually observed in an electrochemical system. The results shown in Figs. 12 and 13 represent major experimental achievements in both cases [68–70]. The central problem that had to be overcome was that, for many combinations of solvent and redox couple, the bimolecular rate constants for electron transfer were obscured by diffusion control. However, the diffusion-controlled rate constant for the solvated electron in tetrahydrofuran (THF) is very high (1.7 × 10¹¹ L mol⁻¹ s⁻¹) due to the small size of the solvated electron and the low viscosity of the solvent. This fact permitted Abdul Kadhum and Arthur Salmon to report the first incontrovertible observation of the inverted region of electron transfer in 1982 [68]. The rate constants for the reaction of solvated electrons with various solutes were measured in tetrahydrofuran at 22 °C, and the results are shown in Fig. 12.

Fig. 12

The first experimental observation of the inverted region. Second-order rate constants for electron transfer from solvated electrons to various solutes in THF at room temperature, plotted as a function of electron affinity of solute (driving force). The solvent dielectric constant was 7.52. (1) Phenol, (2) 4-aminobenzonitrile, (3) 2,4,6-trimethylpyridine, (4) pyridine, (5) α-methylstyrene, (6) benzonitrile, (7) pyrimidine, (8) biphenyl, (9) trans-stilbene, (10) pyrene, (11) nitrobenzene, (12) m-dinitrobenzene, (13) tetranitromethane, (14) p-benzoquinone, (15) tetracyanoethylene, (16) galvinoxyl, and (17) 2,2-diphenyl-1-picrylhydrazyl. Data from Abdul A.H. Kadhum and G. Arthur Salmon [68]

Fig. 13

Experimental first-order rate constants for electron transfer as a function of the total Gibbs energy change. Electrons transferred intramolecularly across various internally bridged bifunctional molecules in 2-methyl tetrahydrofuran at 296 K. The solvent dielectric constant was 6.97. Data obtained by a pulse radiolysis technique. Data derived from John R. Miller et al. [69]

A somewhat different approach to establishing the existence of the inverted region was taken by John R. Miller, Lidia T. Calcaterra, and Gerhard Ludwig Closs, who synthesized a homologous series of eight compounds of the general structure A–B–C where A was 4-biphenylyl, B was a nonconjugated “bridge,” and C was one of a series of eight conjugated moieties [69]. In all the compounds tested, the distances between A and C were about the same (1.0 nm edge-to-edge). The experiment involved subjecting solutions of these various molecules to 30-ps pulses of electrons generated by the Argonne 20-MeV Linac. The electrons were then captured by either A or C with almost 100% efficiency, thus permitting the rate constants for intramolecular electron transfer to be estimated by measuring how fast the perturbed system relaxed back to equilibrium. The results are shown in Fig. 13. This elegant experiment established that, in addition to intermolecular electron transfer, an inverted region could also be observed for intramolecular electron transfer.

In systems where the acceptor molecule has a low-lying excited state, the presence of an inverted region may also trigger chemiluminescence. Chemiluminescence is the emission of light from a chemical reaction, greater than the background emission caused by black body radiation. Typical conditions that trigger chemiluminescence are illustrated in Fig. 14. In the example shown, the activation energy for electron transfer to the excited state is actually less than the activation energy for electron transfer to the ground state, so that the excited state of the product is preferentially populated. When that happens, the electron in the excited state can decay to the ground state by emitting a photon of light.

Fig. 14

The origin of chemiluminescence. Plot of Gibbs energy versus reaction coordinate for homogeneous electron transfer in an electrolyte solution, in the case of a highly exergonic reaction. Note that electron transfer into the ground state of the product is inhibited by the inverted region, but electron transfer into the excited state of the product is not. As a result, the excited state decays by emission of a photon

Finally, it should be noted that an inverted region is not predicted to occur in the case of heterogeneous electron transfer from a metal electrode to a species in solution because of the presence of a quasicontinuum of electronic states inside the metal surface. The situation is illustrated in Fig. 15. In this case, it is obvious that, for a highly exergonic reaction, electron transfer will instead take place from one of the many energy levels available below the Fermi energy.

Fig. 15

Plot of Gibbs energy versus reaction coordinate for heterogeneous electron transfer from a metal electrode to a neutral species in solution, in the case of a highly exergonic reaction. Here, various Gibbs energies of electrons have been added to the Gibbs energy of the reactant, producing the manifold of curves in the center of the diagram. Due to the large number (quasicontinuum) of energy levels in the metal, electron transfer can take place readily from an energy level below the Fermi energy without thermal activation. This activationless electron transfer process prevents inverted kinetics from being observed on metal electrodes

Quantum theory of electron transfer

Equalization of the energies of donor and acceptor states is the crucial first step in electron transfer, and we have now described several models of it. In this section, we focus on the electron tunneling process itself.

After the donor and the acceptor states have equalized their energies, the wave function of the electron becomes time dependent and starts to build up inside the acceptor. By the Born interpretation, the probability of finding the electron also builds up inside the acceptor. In order to describe this process mathematically and to develop a complete expression for the rate of electron transfer, we must find an acceptable solution to the time-dependent Schrödinger equation. Unfortunately, this is not so easy. In order to succeed, we shall find it necessary to employ a severe approximation (the pseudopotential approximation) to reduce the many-electron problem to a single-electron problem. Then, to force a solution, we shall also need to use Paul Dirac’s first-order perturbation theory. Along the way, we shall additionally have to confront a number of conceptual difficulties, not the least of which is the uncertainty principle.

The idea behind the pseudopotential approximation is to replace the complicated effects of all the electrons in a molecule (except one) with an effective potential, or pseudopotential, so that the Schrödinger equation may be solved more readily. In particular, the outermost electron is assumed to move in the electrostatic field of the nuclei and in the average field of all the other electrons. The innermost electrons are thereby removed from consideration, and all the focus is on the single electron in the highest occupied molecular orbital. In the present work, we shall adopt this approach, and we shall also use the simplest possible shape of pseudopotential, namely a rectangular potential well.

The uncertainty principle

The uncertainty principle asserts that one cannot simultaneously measure the values of a pair of conjugate quantum state properties to better than a certain limit of accuracy [4]. There is a minimum for the product of the uncertainties. Key features of pairs of conjugate quantum state properties are that they are uncorrelated and, when multiplied together, have the dimensions of action (energy × time). Examples are (1) momentum and location and (2) energy and lifetime. Thus,

$$ \Delta p\;\Delta x \geqslant {\hbar \mathord{\left/{\vphantom {\hbar 2}} \right.} 2} $$

(5.1)

$$ \Delta U\;\Delta t \geqslant {\hbar \mathord{\left/{\vphantom {\hbar 2}} \right.} 2} $$

(5.2)

Here, p is momentum of a particle (in one dimension); x is location of a particle (in one dimension); U is energy of a quantum state; t is lifetime of a quantum state; and ħ is the reduced Planck constant,

$$ \hbar = \frac{h}{{2\pi }} = 0.6582\;\;\left( {{\hbox{eV}} \times {\hbox{fs}}} \right) $$

(5.3)

The formal and general proof of the above inequalities was first given by Howard Percy Robertson in 1929 [71]. He also showed that the uncertainty principle was a deduction from quantum mechanics, not an independent hypothesis.

As a result of the “blurring” effect of the uncertainty principle, quantum mechanics is unable to predict the precise behavior of a single electron at short times. But it can still predict the average behavior of a large number of electrons at short times, and it can also predict the time-averaged behavior of a single electron over long times. From the above equations, the energy measured over a finite time interval ∆t has an uncertainty

$$ \Delta U \geqslant \frac{\hbar }{{2\Delta t}} $$

(5.4)

and therefore to decrease the energy uncertainty of an electron to practical insignificance (<1 meV, say, which is equivalent to about 1.602 × 10⁻²² J per electron), it is necessary to observe it for t > 330 fs. Conversely, if we wish to observe the motion of electrons with femtosecond accuracy, then we have to accept uncertainties in their energy of the order of 1 eV.

Wave mechanics

As proposed by Erwin Schrödinger [3], the total wave function Ψ of a (nonrelativistic) electron may be obtained by solving the time-dependent equation

$$ H\Psi = \left( {i\hbar } \right)\frac{{\partial \Psi }}{{\partial t}} $$

(5.5)

Here, H is the differential operator known as the Hamiltonian, which takes the form

$$ H\Psi = - \frac{{{\hbar^2}}}{{2m}}{\nabla^2}\Psi - {\hbox{e}}V\,\Psi $$

(5.6)

where m is the electron mass; −e is the electron charge; and V is the electrostatic potential.

Note that the electrostatic potential at a particular point in space (x, y, z), created by a system of charges, is just the change in potential energy that would occur if a test charge of +1 were introduced at that point. So −eV is the electrostatic potential energy of the electron in the electric field. The Laplacian ∇², which also appears in the Schrödinger equation, is the square of the vector operator ∇(“del”), defined in Cartesian coordinates by

$$ \nabla \phi \left( {x,y,z} \right) = \frac{{\partial \phi }}{{\partial x}}\hat x + \frac{{\partial \phi }}{{\partial y}}\hat y + \frac{{\partial \phi }}{{\partial z}}\hat z $$

(5.7)

As mentioned earlier, every solution of the Schrödinger equation represents a possible state of the system. There is, however, always some uncertainty associated with the manifestation of each state. Due to the uncertainty, the square of the modulus of the wave function |Ψ|² may be interpreted in two ways. Firstly and most abstractly, as the probability that an electron might be found at a given point. Secondly and more concretely, as the electric charge density at a given point (averaged over a large number of identically prepared systems for a short time or averaged over one system for a long time).

Remark

Almost all kinetic experiments in physics and chemistry lead to statements about the relative frequencies of events, expressed either as deterministic rates or as statistical transition probabilities. In the limit of large systems, these formulations are, of course, equivalent. By definition, a transition probability is just the probability that one quantum state will convert into another quantum state in a single step.

Time-dependent perturbation theory

It is an unfortunate fact of quantum mechanics that exact mathematical solutions of the time-dependent Schrödinger equation are possible only at the very lowest levels of system complexity. Even at modest levels of complexity, mathematical solutions in terms of the commonplace functions of applied physics are impossible. The recognition of this fact caused great consternation in the early days of quantum mechanics. To overcome the difficulty, Paul Dirac developed an extension of quantum mechanics called “perturbation theory,” which yields good approximate solutions to many practical problems [72]. The only limitation on Dirac’s method is that the coupling (orbital overlap) between states should be weak.

The key step in time-dependent perturbation theory is to split the total Hamiltonian into two parts, one of which is simple and the other of which is small. The simple part consists of the Hamiltonian of the unperturbed fraction of the system, which can be solved exactly, while the small part consists of the Hamiltonian of the perturbed fraction of the system, which, though complex, can often be solved as a power series. If the latter converges, solutions of various problems can be obtained to any desired accuracy simply by evaluating more and more terms of the power series. Although the solutions produced by Dirac’s method are not exact, they can nevertheless be extremely accurate.

In the case of electron transfer, we imagine a transition between two well-defined electronic states, an occupied state |D〉 inside an electron donor D, and an unoccupied state |A〉 inside an electron acceptor A. The central problem is then to determine how the wave function of the electron builds up inside the unoccupied state |A〉.

Electron transfer between single states

The problem of modeling electron transfer between single states has exercised the minds of chemists ever since the earliest days of quantum theory. Today, the theory has reached its highest state of development in the field of spectroscopy. However, in spectroscopy, the transitions are intramolecular, i.e., they occur between two allowed states inside one electrostatic potential well, and the perturbation that triggers the transition is typically the arrival of a photon. In electrochemistry, the problem is of a different type. The transitions are intermolecular, i.e., between two allowed states inside two different electrostatic potential wells, and the perturbation is typically the arrival of one potential well within electron tunneling distance of the other.

If classical physics prevailed, the intermolecular transfer of an electron from one single state to another single state would be governed by the conservation of energy and would occur only when both states had exactly the same energy. But in the quantum world, the uncertainty principle (in its time–energy form) briefly intervenes and allows electron transfer between states even when their energies are mismatched by a small amount $\Delta U = \hbar /2\Delta t$ (although energy conservation still applies on average). As a result of this complication, the transition probability of electrons between two states exhibits a complex behavior. Roughly speaking, the probability of electron transfer between two precise energies inside two specified states has a component that increases as t ², while the energy uncertainty decreases as t ⁻¹. The net result is that the overall state-to-state transition probability increases proportional to t.

To make these ideas precise, consider a perturbation which is “switched on” at time t = 0 and which remains constant thereafter. This perturbation might be, for example, a change in the electrostatic potential energy of the system induced by the movement of a nearby charged species into a new location. This introduces a perturbation H’ into the Hamiltonian, so that the time-dependent Schrödinger equation becomes

$$ \left( {i\hbar } \right)\frac{{\partial \Psi }}{{\partial t}} = \left( {{H_0} + H\prime} \right)\Psi $$

(5.8)

where Ψ(x, t) is the total electron wave function; H ₀ is the unperturbed part of the total Hamiltonian operator; and H′ is the perturbed part of the total Hamiltonian operator.

Remark

The total electron wave function Ψ(x, t) may be regarded as the linear superposition of the individual wave functions of all the possible states of the system, modified by appropriate weighting coefficients a _k. Thus,

$$ \Psi \left( {x,t} \right) = \sum {{a_{\rm{k}}}(t){\psi_{\rm{k}}}\left( {x,t} \right)} $$

(5.9)

By the Born interpretation, |a _k(t)|² is the probability that the electron will manifest in the kth state when the system interacts with the external world. The fact that the system randomly localizes in a particular state k when it is perturbed is called “the collapse of the wave function.” For a two-state donor–acceptor system, the probability that the electron localizes in the acceptor state is, of course, just the probability that the electron delocalizes from the donor state.

Now, according to our model, H′(t) has the following form,

$$ H\prime(t) = 0\quad {\hbox{for}}\quad t < 0 $$

(5.10)

$$ H\prime(t) = H\prime\quad {\hbox{for}}\quad t \geqslant 0 $$

(5.11)

That is, H′(t) is a step function with a constant value at t ≥ 0. Solving Eq. 5.8 under these boundary conditions, the probability of electron transfer between two specified energies U _D and U _A is

$$ {P_{\rm{DA}}}\left( {U,\,t} \right) \approx \frac{{2{{\left| {{{H\prime}_{\rm{DA}}}} \right|}^2}}}{{{{\left| {{U_{\rm{A}}} - {U_{\rm{D}}}} \right|}^2}}}\left[ {1 - \cos \left( {\frac{{\left[ {{U_{\rm{A}}} - {U_{\rm{D}}}} \right]t}}{\hbar }} \right)} \right] $$

(5.12)

where the modulus symbol denotes the (always positive) magnitude of any complex number. This probability is oscillatory and decays to 0 as time progresses, unless of course U _D = U _A. This is the quantum equivalent of the conservation of energy. The term ${H\prime_{\rm{DA}}}$ is commonly known as the “matrix element” of the donor–acceptor interaction and is characteristic for a particular interaction. It has units of energy and is related to the perturbation $H\prime$ by the equation

$$ H_{\rm{DA}}\prime = \int {\psi_{\rm{A}}^*} H\prime{\psi_{\rm{D}}}{\hbox{d}}\tau $$

(5.13)

or, in Dirac’s compact notation,

$$ H_{\rm{DA}}\prime = < {{\psi_{\rm{A}}}\left| {H\prime} \right|{\psi_{\rm{D}}}} > $$

(5.14)

In these equations, ψ _D and ψ _A are the wave functions of the donor state and acceptor state, respectively. As always, the asterisk indicates a complex conjugate, and the integral over dτ indicates an integral over all space.

In many cases in the scientific literature in which perturbation theory is applied to physical events, the meaning of the matrix element $H_{\rm{DA}}\prime$ is far from clear. Sometimes, it is referred to as the “coupling” between the donor and the acceptor states, but that description adds little to our understanding. However, in the special case under consideration here, the electron localizes inside an acceptor orbital; and, to a first approximation, the latter can be modeled as a rectangular potential well whose potential is constant and equal to that of the donor orbital. This allows H′ to be transposed out of the integral to yield

$$ H_{\rm{DA}}\prime = H\prime\int {\psi_{\rm{A}}^*} {\psi_{\rm{D}}}{\hbox{d}}\tau $$

(5.15)

or, in Dirac notation,

$$ H_{\rm{DA}}\prime = H\prime< {{\psi_{\rm{A}}}\left| {{\psi_{\rm{D}}}} \right.} > $$

(5.16)

In this special case, the meaning of $H_{\rm{DA}}\prime$ is unusually clear. It is simply a measure of the extent to which the donor and acceptor wave functions constructively interfere (“overlap”). Indeed, the term

$$ {S_{\rm{DA}}} = < {{\psi_{\rm{A}}}\left| {{\psi_{\rm{D}}}} \right.} > $$

(5.17)

is widely referred to in molecular orbital theory as the overlap integral.

Orbital overlap

The emergence of the overlap integral at the very heart of electron transfer theory emphasizes the crucial role that orbital overlap plays in determining the rates of electron transfer reactions. Recall that the wave functions of donor and acceptor states always have regions of both positive and negative amplitude. It follows that if a donor–acceptor interaction involves only positive or only negative overlap, then the overlap integral S _DA is finite, and electron transfer is strongly favored (“symmetry-allowed”). Conversely, if the donor–acceptor interaction involves roughly equal amounts of positive and negative overlap, then the overlap integral consists of two terms that nearly cancel, and electron transfer is strongly disfavored (“symmetry-disallowed”). An example of symmetry-disallowed electron transfer is illustrated in Fig. 16.

Fig. 16

Diagram to illustrate symmetry-disallowed electron transfer between an s-type donor orbital ψ _D and a p _z-type acceptor orbital ψ _A. In this case, the overlap integral S _DA vanishes because the contributions from the volume elements dτ₁ and dτ₂ are of opposite sign and hence cancel

As a result of symmetry considerations, the angle of interaction between donor and acceptor orbitals becomes a factor in determining the rate of electron transfer. The distance between the donor and acceptor orbitals also has a very strong effect. Accordingly, for electron transfer between ions in solution (or between an electrode and ions in solution), it is obvious that in practice only a mean rate of electron transfer is actually measured in the laboratory, with the experimental results representing a sum over an unknown range of internuclear angles and a sum over an unknown range of internuclear distances.

Some examples of symmetry-allowed combinations of donor and acceptor orbitals are collected in Table 7, assuming that electron transfer is confined to the x-direction. Similar tables could of course be constructed for electron transfer confined to the y-direction and the z-direction. Although the table neglects the possibility of an experimental dispersion of internuclear angles, it does bring to light one very important fact, which is that some pairs of orbitals are much more reactive than others towards electron transfer. It is evident that orbital symmetries must be properly matched for electron transfer to occur at a significant rate.

Table 7 Symmetry-allowed combinations of donor and acceptor orbitals in electron transfer

The simplest geometric measure of an electron transfer system is the internuclear separation between the donor and acceptor species. Unfortunately, there is no easy solution to the problem of how this parameter affects the value of the overlap integral S _DA. However, it has been found by innumerable ab initio quantum chemical calculations that electron wave functions decay with a mixed exponential/power-law functional form in the radial direction away from atomic nuclei. This is, indeed, the basis of several approximate methods in molecular simulation, based on “Slater-type orbitals.” These are named after the physicist John C. Slater who introduced them in 1930 [73]. Although Slater-type orbitals were originally designed for use in the computation of wave functions of atomic and diatomic systems, they are often used today as trial solutions for the wave functions of polyatomic systems, and the exponential decay of the wave functions of Slater-type orbitals at large r is widely thought to carry over into larger systems.

Considering only the radial component of a wave function, a typical Slater approximation takes the form

$$ \psi (r) = N{r^{n - 1}}\exp \left( { - \xi r} \right) $$

(5.18)

where N is a normalization constant; n is a natural number (1, 2, 3…) similar to the principal quantum number; ξ (zeta) is a constant related to the shielding of nuclear forces by low-lying electrons; and r is a distance coordinate measured from the atomic nucleus. Given this mixed exponential/power-law decay of the wave function of a single electron, it seems reasonable to conjecture that the overlap integral decays in a similar way, yielding the asymptotic approximation

$$ {S_{\rm{DA}}} \approx A{x^{\rm{B}}}\exp \left( { - Cx} \right) $$

(5.19)

where x is the internuclear separation. Even more complex behavior is expected at short range or if there is an interaction with a third electronic state.

The effects of orbital overlap become most apparent when homologous series of redox reactions are investigated. As an example, let us compare the electron self-exchange reactions of the 1,10-phenanthroline complexes of the Co(II)/Co(III) and the Fe(II)/Fe(III) couples. Note that the 1,10-phenanthroline ligand has a high field strength, and so its octahedral complexes are low spin [74].

The electronic structure of the Fe(II) ion is (Ar) 3d ⁶. By contrast, Co(II) has an additional proton in its nucleus and therefore an additional electron in its d-orbitals, yielding the electronic structure (Ar) 3d ⁷. In the case of low-spin octahedral complexes, this compels the Co(II) ion to place its seventh and outer electron into an e _g state, either a z ² orbital or a x ² − y ² orbital. On the other hand, the Fe(II) ion can accommodate all six of its d-electrons in t _2g states (see Fig. 17).

Fig. 17

Electronic configuration and relative orientation of d-orbitals in octahedral complexes of first-row transition elements. For low-spin complexes, the first six electrons are found in t _2g states. But the seventh electron occupies an e _g state

Due to the large size of the 1,10-phenanthroline ligands, the redox metal centers cannot approach each other closer than about 1.4 nm. This means that the probability of direct electron transfer between them is low. On the other hand, indirect electron transfer may readily take place via the π* orbital of the 1,10-phenanthroline ligand if there is symmetry-allowed overlap between the highest occupied molecular orbital of the redox metal center and the lowest unoccupied molecular orbital of the ligand. As it happens, there is very good overlap between the t _2g orbitals of Fe(II) and the π* orbitals of the 1,10-phenanthroline ligands, but there is very poor overlap between the e _g orbitals of Co(II) and the π* orbitals of the 1,10-phenanthroline ligands. This explains the following seemingly disparate rate constants [75, 76]:

$$ \begin{array}{*{20}{c}} {{\hbox{Co}}\left( {\hbox{phen}} \right)_3^{{3} + } + {\hbox{Co}}\left( {\hbox{phen}} \right)_3^{{2} + }} & { \leftrightarrows {\hbox{Co}}\left( {\hbox{phen}} \right)_3^{{2} + } + {\hbox{Co}}\left( {\hbox{phen}} \right)_3^{{3} + }} & {\left[ {{k_{\rm{et}}} = 12\;{\hbox{Lmo}}{{\hbox{l}}^{ - 1}}{{\hbox{s}}^{ - 1}}} \right]} \\{{\hbox{Fe}}\left( {\hbox{phen}} \right)_3^{{3} + } + {\hbox{Fe}}\left( {\hbox{phen}} \right)_3^{{2} + }} & { \leftrightarrows {\hbox{Fe}}\left( {\hbox{phen}} \right)_3^{{2} + } + {\hbox{Fe}}\left( {\hbox{phen}} \right)_3^{{3} + }} & {\left[ {{k_{\rm{et}}} = 1.3 \times {{10}^7}\;{\hbox{Lmo}}{{\hbox{l}}^{ - 1}}{{\hbox{s}}^{ - 1}}} \right]} \\\end{array} $$

We see that the cobalt redox couple reacts more than a million times slower than the iron redox couple, despite having an unpaired electron in its outermost orbital! It is evident that orbital symmetry is very important indeed.

The above results have no classical rationale and can be explained only by quantum mechanics. A corollary is that attempts to find purely classical relationships (“cross-relations”) between homologous pairs of redox reactions, based on neglect of quantum mechanics, are doomed to failure.

Finally, we may summarize the results of this section by stating the three quantum conditions for successful electron transfer:

• 1. The wave functions must overlap.

• 2. The wave functions must have the same energy.

• 3. The wave functions must interfere constructively.

Interfacial electron transfer

From the quantum theory of electron transfer, we have found that the probability of electron transfer between two specified energies U _D and U _A can be written in the form

$$ {P_{\rm{DA}}}\left( {U,\,t} \right) \approx \frac{{2{{\left| {{{H\prime}_{\rm{DA}}}} \right|}^2}}}{{{{\left| {{U_{\rm{A}}} - {U_{\rm{D}}}} \right|}^2}}}\left[ {1 - \cos \left( {\frac{{\left[ {{U_{\rm{A}}} - {U_{\rm{D}}}} \right]t}}{\hbar }} \right)} \right] $$

(6.1)

This probability is oscillatory and decays to 0 as time progresses, unless U _D = U _A, in which case the probability grows with time. We have also found that the matrix element $H_{\rm{DA}}\prime$ can be approximated by the expression

$$ \begin{array}{*{20}{c}} {H_{\rm{DA}}\prime} & { \approx H\prime\int {\psi_{\rm{A}}^*{\psi_{\rm{D}}}d\tau } } \\{} & { \approx H\prime{S_{\rm{DA}}}} \\\end{array} $$

(6.2)

where S _DA is an overlap integral.

In the present section, we apply these results to the case of heterogeneous (interfacial) electron transfer. We also describe how multitudes of states can be accommodated by the theory.

We begin by noting the identity

$$ 1 - \cos x = 2{\sin^2}\left( {{x \mathord{\left/{\vphantom {x 2}} \right.} 2}} \right) $$

(6.3)

which allows us to cast Eq. 6.1 into the slightly modified form

$$ {P_{\rm{DA}}}\left( {U,\,t} \right) \approx \frac{{4{{\left| {{{H\prime}_{\rm{DA}}}} \right|}^2}}}{{{{\left| {{U_{\rm{A}}} - {U_{\rm{D}}}} \right|}^2}}}{\sin^2}\left( {\frac{{\left[ {{U_{\rm{A}}} - {U_{\rm{D}}}} \right]t}}{{2\hbar }}} \right) $$

(6.4)

Furthermore, by recalling the definition of the cardinal sine function,

$$ {\hbox{sinc}}(x) = \frac{{\sin x}}{x} $$

(6.5)

we can simplify the result still further:

$$ {P_{\rm{DA}}}\left( {U,\,t} \right) \approx \frac{{{{\left| {{{H\prime}_{\rm{DA}}}} \right|}^2}{t^2}}}{{{\hbar^2}}}{ \sin }{{\hbox{c}}^2}\left( {\frac{{\left[ {{U_{\rm{A}}} - {U_{\rm{D}}}} \right]t}}{{2\hbar }}} \right) $$

(6.6)

Equation 6.6 gives the time evolution of the probability of electron transfer from the very earliest times, including the effects of the uncertainty principle. In electrochemistry, we are more concerned with longer times, when the effects of the uncertainty principle have decayed away. In that limit, Dirac [72] showed that

$$ {P_{\rm{DA}}}(t) \approx \frac{{2\pi t}}{\hbar }{\left| {{{H\prime}_{\rm{DA}}}} \right|^2}\delta \left( {{U_{\rm{A}}} - {U_{\rm{D}}}} \right) $$

(6.7)

where δ is the delta function. This formula is justly famous because it allows the theory of single acceptor states to be extended to multiple acceptor states.

Multiple acceptor states

To deal with this more complex case, it is necessary to define a probability density of acceptor state energies φ _A(U). Accordingly, we define φ _A(U) as the number of acceptor states per unit of energy, and note that it has units of joule⁻¹ (dimensions of energy⁻¹). If we further assume that there is such a high density of states that it can be treated as a continuum, then the transition probability between the single-donor state |D〉 and the multitude of acceptor states |A〉 becomes

$$ {P_{\rm{DA}}}(t) \approx \frac{{2\pi t}}{\hbar }{\left| {{{H\prime}_{\rm{DA}}}} \right|^2}{\varphi_{\rm{A}}}\left( {{U_{\rm{D}}}} \right) $$

(6.8)

where U _D, the single energy of the donor state, is a constant.

Remark

The parameter φ _A(U _D) in Eq. 6.8 is not the full density-of-states function φ _A(U) that it is often stated to be in the literature. It is, in fact, the particular value of the density-of-states function at the energy U _D.

Finally, in the ultimate simplification of the theory, it is possible to derive the rate constant for electron transfer k _et by differentiating the transition probability. This yields

$$ {k_{\rm{et}}} = \frac{{2\pi }}{\hbar }{\left| {{{H\prime}_{\rm{DA}}}} \right|^2}{\varphi_{\rm{A}}}\left( {{U_{\rm{D}}}} \right) $$

(6.9)

It was Enrico Fermi who first referred to this equation as a “golden rule” (in 1949), and the epithet has stuck [77]. The result, however, is due to Dirac [78].

Remark

The golden rule applies only to cases where electron transfer occurs from a single-donor state into a multitude of acceptor states. If electrons originate from a multitude of donor states—as they do during redox reactions in electrolyte solutions—then the transition probabilities must be summed (integrated) over the density of states of the donor, viz.

$$ {k_{\rm{et}}} = \int_{-\infty }^{ + \infty } {\frac{{2\pi }}{\hbar }{{\left| {{{H\prime}_{\rm{DA}}}} \right|}^2}{\varphi_{\rm{A}}}\left( {{U_{\rm{D}}}} \right)} {\varphi_{\rm{D}}}\left( {{U_{\rm{D}}}} \right){\hbox{d}}{U_{\rm{D}}} $$

(6.10)

For all molecules in solution, their densities of states arise from the random thermal motion of surrounding charged species. As a result, their electrostatic potentials vary billions of times every second.

The distribution of acceptor states

Ludwig Boltzmann brought the study of fluctuations inside equilibrium systems to a high state of development in the late nineteenth century [79]. Indeed, his methods are so general that they can be applied to any small system in thermal equilibrium with a large reservoir of heat. In our case, they permit us to calculate the probability that a randomly selected electrostatic fluctuation has a work of formation ΔG.

A system (such as an electrolyte solution) is in equilibrium if the requirements of detailed balance are satisfied, namely, that every process taking place in the system is exactly balanced by its reverse process, so there is no net change over time. This implies that the rate of formation of fluctuations matches their rate of dissipation. In other words, the fluctuations must have a distribution that is stationary. As a result, at thermodynamic equilibrium, we know in advance that the probability density function of any fluctuations must be independent of time.

Boltzmann discovered a remarkable property of fluctuations that occur inside systems at thermal equilibrium: their probability always contains the “Boltzmann factor,”

$$ \exp \left( {\frac{{ - \Delta W}}{{{k_{\rm{B}}}T}}} \right) $$

(6.11)

where ΔW is an appropriate thermodynamic potential; k _B is the Boltzmann constant; and T is the thermodynamic (absolute) temperature. At constant temperature and pressure, ΔW is the Gibbs energy of formation of the fluctuation along the reaction coordinate, ΔG _RC. Given this knowledge, it follows that the probability density function φ _A(V) of electrostatic potentials (V) must have the stationary form

$$ {\varphi_{\rm{A}}}(V) = A\exp \left( {\frac{{ - \Delta {G_{\rm{RC}}}}}{{{k_{\rm{B}}}T}}} \right) $$

(6.12)

where A is a time-independent constant. In the case of charge fluctuations that trigger electron transfer, we have

$$ \Delta {G_{\rm{RC}}} = \frac{1}{2}C{\left( {\Delta V} \right)^2} = \frac{1}{2}\frac{{{{\left( {\Delta V} \right)}^2}}}{\Lambda } $$

(6.13)

where C is the capacitance between the reactant species (including its ionic atmosphere) and infinity, and Λ is the elastance (reciprocal capacitance) between the reactant species and infinity. Defining Λe ²/2 as the reorganization energy λ, we immediately obtain

$$ {\varphi_{\rm{A}}}(V) = A\exp \left( {\frac{{ - {{\left( {eV - e{V_{\rm{A}}}} \right)}^2}}}{{4\lambda \,{k_{\rm{B}}}T}}} \right) $$

(6.14)

which means we now have to solve only for A. An elegant method of solving for A is based on the observation that φ_A(V) must be a properly normalized probability density function, meaning that its integral must equal 1. This yields

$$ A = \sqrt {{\frac{{{e^2}}}{{4\pi \lambda \,{k_{\rm{B}}}T}}}} $$

(6.15)

so that

$$ {\varphi_{\rm{A}}}(V) = \frac{e}{{\sqrt {{4\pi \lambda \,{k_{\rm{B}}}T}} }}\exp \left( {\frac{{ - {{\left( {eV - e{V_{\rm{A}}}} \right)}^2}}}{{4\lambda \,{k_{\rm{B}}}T}}} \right) $$

(6.16)

We are now just one step from our goal, which is the probability density of the energies of the acceptor states. We merely need to introduce the additional fact that, if an electron is transferred into an acceptor state whose electric potential is V, then the electron’s energy must be −eV because the charge on the electron is −e. Thus,

$$ {\varphi_{\rm{A}}}\left( { - eV} \right) = \frac{1}{{\sqrt {{4\pi \lambda \,{k_{\rm{B}}}T}} }}\exp \left( {\frac{{ - {{\left( {eV - e{V_{\rm{A}}}} \right)}^2}}}{{4\lambda \,{k_{\rm{B}}}T}}} \right) $$

(6.17)

or, writing U = −eV,

$$ {\varphi_{\rm{A}}}(U) = \frac{1}{{\sqrt {{4\pi \lambda \,{k_{\rm{B}}}T}} }}\exp \left( {\frac{{ - {{\left( {U - {U_{\rm{A}}}} \right)}^2}}}{{4\lambda \,{k_{\rm{B}}}T}}} \right) $$

(6.18)

where U is the electron energy. This equation gives the stationary, normalized probability density of the energies of the acceptor states in a reactant species in an electrolyte solution. It is a Gaussian density. If required, we can readily get the unnormalized result simply by multiplying φ _A(U) by the surface concentration of acceptor species. Finally, we note that the corresponding formula for φ _D(U) is also Gaussian

$$ {\varphi_{\rm{D}}}(U) = \frac{1}{{\sqrt {{4\pi \lambda \,{k_{\rm{B}}}T}} }}\exp \left( {\frac{{ - {{\left( {U - {U_{\rm{D}}}} \right)}^2}}}{{4\lambda \,{k_{\rm{B}}}T}}} \right) $$

(6.19)

where we have assumed that λ _A = λ _D = λ.

Rate constant for homogeneous electron transfer

Combining Eqs. 6.9 and 6.19, at constant temperature and pressure, we obtain

$$ {k_{\rm{et}}} = \frac{{2\pi }}{\hbar }{\left| {{{H\prime}_{\rm{DA}}}} \right|^2}\frac{1}{{\sqrt {{4\pi \lambda \,{k_{\rm{B}}}T}} }}\exp \left( {\frac{{ - \Delta G_{\rm{RC}}^{*}}}{{{k_{\rm{B}}}T}}} \right) $$

(6.20)

where k _et is the rate constant for electron transfer; $H_{\rm{DA}}\prime$ is the electronic coupling matrix element between the electron donor and acceptor species; k _B is the Boltzmann constant; λ is the sum of the reorganization energies of the donor and acceptor species; and $\Delta G_{\rm{RC}}^{*}$ is the “Gibbs energy of activation” for the reaction along the reaction coordinate.

Referring to Fig. 18, it is clear that $\Delta G_{\rm{RC}}^{*}$ is the total Gibbs energy that must be transferred from the surroundings to both reactants in order to bring them to their mutual transition states along the reaction coordinate. This is simply

$$ \Delta G_{\rm{RC}}^{*} = \frac{{{{\left( {\lambda + \Delta {G^0}} \right)}^2}}}{{4\lambda }} $$

(6.21)

which implies that

$$ {k_{\rm{et}}} = \frac{{2\pi }}{\hbar }{\left| {{{H\prime}_{\rm{DA}}}} \right|^2}\frac{1}{{\sqrt {{4\pi \lambda \,{k_{\rm{B}}}T}} }}\exp \left( {\frac{{ - {{\left( {\lambda + \Delta {G^0}} \right)}^2}}}{{4\lambda \,{k_{\rm{B}}}T}}} \right) $$

(6.22)

This equation is the central result of the modern theory of quantum electrochemistry. It corresponds to the golden rule formula of Dirac in the special case that the distribution of acceptor states is Gaussian.

Fig. 18

Gibbs energy diagram for homogeneous one-electron transfer between two noninteracting species in solution. As defined in the present work, the symmetry factor β corresponds to the fractional charge of the fluctuation on the ionic atmosphere of the acceptor molecule at the moment of electron transfer. After Fletcher [22]

An equation of the form of Eq. 6.22 was first published by Veniamin Levich and Revaz Dogonadze in 1959 [80]. Shortly afterwards, in 1962, the theory was extended to heterogeneous electron transfer (e.g., to electron transfer at metal electrodes) by Revaz Dogonadze and Yurii Chizmadzhev [81].

We can also define a symmetry factor β such that

$$ \Delta G_{\rm{RC}}^{*} = {\beta^2}\lambda $$

(6.23)

and therefore

$$ \beta = \frac{{{\text{d}}\,\Delta G_{\rm{RC}}^*}}{{{\hbox{d}}\,\Delta {G^0}}} = \frac{1}{2}\left( {1 + \frac{{\Delta {G^0}}}{\lambda }} \right) $$

(6.24)

Remark

β = 1/2 approximately if ΔG⁰ is sufficiently small (i.e., the electron transfer reaction is neither strongly exergonic nor strongly endergonic), and β = 1/2 exactly for a self-exchange reaction (ΔG⁰ = 0).

Combining Eqs. 5.19 and 6.2, we also obtain

$$\begin{aligned} & H^{\prime }_{{DA}} \approx H\prime S_{{DA}} \\ & \quad \,\,\,\, \approx Hx^{B} \exp {\left( { - Cx} \right)} \\ \end{aligned} $$

(6.25)

where x is the distance of closest approach of the donor and acceptor (i.e., a function of the ionic strength of the solution).

The validity of the Gibbs energy diagram in Fig. 18 relies on the existence of friction between the reactant species and the environment. This is consistent with the fact that each reactant species continually and randomly exchanges energy with the electrolyte solution and thus causes stochastic motion along the reaction coordinate. If we had used a potential energy diagram instead, this would have implied the nonexistence of friction between the reactant species and the environment. And in that case, each reactant species would conserve its own energy and hence would exhibit deterministic motions (such as harmonic oscillations) along the reaction coordinate.

In transition-state theory, it is assumed that the continual and random exchange of energy between the reactant species and the electrolyte solution is always fast enough to maintain the equilibrium population of reactant species at all points along the Gibbs energy surface, so that the high-energy population is never depleted by the electron transfer process. The opposite situation, in which the high-energy population of reactant species on the Gibbs energy diagram is actually depleted by the electron transfer process, is known as Kramer’s problem [82]. The rate derived from transition-state theory is therefore an upper bound on the solution of Kramer’s problem.

Finally, we note that Fig. 18 also explains why simultaneous two-electron transfer reactions are much rarer than one-electron transfer reactions. All things being equal, they require four times the activation energy. Thus, they are likely to be observed only in those very rare circumstances where the relative disposition of the Gibbs energy curves is such that the electron transfer process is nearly activationless.

Rate constant for heterogeneous electron transfer

In the case of electron transfer across a phase boundary (e.g., electron transfer from an electrode into a solution), the law of conservation of energy dictates that the energy of the transferring electron must be added into that of the acceptor species, such that the sum equals the energy of all the product species. At constant temperature and pressure, the energy of the transferring electron is just its Gibbs energy.

Let us denote by superscript $\overline {bar}$ the Gibbs energies of species in solution after the energy of the transferring electron has been added to them (see Fig. 19). We have

$$ {\overline G_{\rm{reactant}}} = {G_{\rm{reactant}}} + qE $$

(6.26)

$$ {\overline G_{\rm{reactant}}} = {G_{\rm{reactant}}} - eE $$

(6.27)

where e is the unit charge and E is the electrode potential of the injected electron. For the conversion of reactant to product, the overall change in Gibbs energy is

$$ \Delta {\overline G^0} = {\overline G_{\rm{product}}} - {\overline G_{\rm{reactant}}} $$

(6.28)

$$ \Delta {\overline G^0} = {G_{\rm{product}}} - \left( {{G_{\rm{reactant}}} - eE} \right) $$

(6.29)

$$ \Delta {\overline G^0} = \left( {{G_{\rm{product}}} - {G_{\rm{reactant}}}} \right) + eE $$

(6.30)

$$ \Delta {\overline G^0} = \Delta {G^0} + eE $$

(6.31)

Fig. 19

Gibbs energy diagram for heterogeneous one-electron transfer from an electrode to an initially neutral acceptor molecule in solution. The superscript bar indicates that the Gibbs energy of the injected electron has been added to that of the reactant

In the normal region of electron transfer, for a metal electrode, it is generally assumed that the electron tunnels from an energy level near the Fermi energy, implying $eE \approx e{E_{\rm{F}}}$. Thus, for a heterogeneous one-electron transfer process to an acceptor species in solution, we can use the golden rule directly [81],

$$ {k_{\rm{et}}} = \frac{{2\pi }}{\hbar }{\left| {{{H\prime}_{\rm{DA}}}} \right|^2}\frac{1}{{\sqrt {{4\pi \lambda \,{k_{\rm{B}}}T}} }}\exp \left( {\frac{{ - {{\left( {\lambda + \Delta {G^0} + e{E_{\rm{F}}}} \right)}^2}}}{{4\lambda \,{k_{\rm{B}}}T}}} \right) $$

(6.32)

where λ is the reorganization energy of the acceptor species in solution, and eE _F is the Fermi energy of the electrons inside the metal electrode. Or, converting to molar quantities

$$ {k_{\rm{et}}} = \frac{{2\pi }}{\hbar }{\left| {{{H\prime}_{\rm{DA}}}} \right|^2}\frac{{{N_{\rm{A}}}}}{{\sqrt {{4\pi \,{\lambda_{\rm{m}}}RT}} }}\exp \left( {\frac{{ - {{\left( {{\lambda_{\rm{m}}} + \Delta G_{\rm{m}}^0 + F{E_{\rm{F}}}} \right)}^2}}}{{4{\lambda_{\rm{m}}}RT}}} \right) $$

(6.33)

where k _et is the rate constant for electron transfer; ħ is the reduced Planck constant; H _DA is the electronic coupling matrix element between a single-electron donor and a single-electron acceptor; N _A is the Avogadro constant; λ _m is the reorganization energy per mole; $\Delta G_{\rm{m}}^0$ is the difference in molar Gibbs energy between the acceptor and the product; and (−FE _F) is the molar Gibbs energy of the electron that tunnels from the Fermi level of the metal electrode into the acceptor.

Equation 6.33 behaves exactly as we would expect. The more negative the Fermi potential E _F inside the metal electrode (i.e., the more negative the electrode potential), the greater is the rate constant for electron transfer from the electrode into the acceptor species in solution.

Some notational simplification is achieved by introducing the definition

$$ - \eta \equiv \frac{{\Delta G_{\rm{m}}^0}}{F} + {E_{\rm{F}}} $$

(6.34)

where η is called the “overpotential.” With this definition, increasing overpotential η corresponds to increasing rate of reaction. In other words, with this definition, the overpotential is a measure of the “driving force for the reaction.” The same inference may be drawn from the equation

$$ \eta \equiv - \frac{{\Delta \overline G_{\rm{m}}^0}}{F} $$

(6.35)

An immediate corollary is that the condition η = 0 corresponds to zero driving force (thermodynamic equilibrium) between the reactant, the product, and the electrode $(\Delta \overline G_{\rm{m}}^0 = 0)$.

By defining a molar Gibbs energy of activation along the reaction coordinate,

$$ \Delta \overline G_{\rm{m}}^{*} = \frac{{{{\left( {{\lambda_{\rm{m}}} + \Delta G_{\rm{m}}^0 + F{E_{\rm{F}}}} \right)}^2}}}{{4{\lambda_{\rm{m}}}}} $$

(6.36)

$$ = \frac{{{{\left( {{\lambda_{\rm{m}}} - F\eta } \right)}^2}}}{{4{\lambda_{\rm{m}}}}} $$

(6.37)

we can conveniently put Eq. 6.33 into the standard Arrhenius form

$$ {k_{\rm{et}}} = \frac{{2\pi }}{\hbar }{\left| {{{H\prime}_{\rm{DA}}}} \right|^2}\frac{{{N_{\rm{A}}}}}{{\sqrt {{4\pi \,{\lambda_{\rm{m}}}\,RT}} }}\exp \left( {\frac{{ - \Delta \overline G_{\rm{m}}^{*}}}{{RT}}} \right) $$

(6.38)

We can further simplify the analysis by defining the partial derivative ${{\partial \,\Delta \overline G_{\rm{m}}^{*}} \mathord{\left/{\vphantom {{\partial \,\Delta \overline G_{\rm{m}}^{*}} {\partial \,\left( { - F\eta } \right)}}} \right.} {\partial \,\left( { - F\eta } \right)}}$ at constant $\Delta G_{\rm{m}}^0$ as the symmetry factor β, so that

$$ \Delta \overline G_{\rm{m}}^{*} = {\beta^2}{\lambda_{\rm{m}}} $$

(6.39)

where

$$ \beta = \frac{{\partial \,\Delta \overline G_{\rm{m}}^{*}}}{{\partial \,\left( { - F\eta } \right)}} = \frac{1}{2}\left( {1 - \frac{{F\eta }}{{{\lambda_{\rm{m}}}}}} \right) $$

(6.40)

This latter equation highlights the remarkable fact that electron transfer reactions require less thermal activation energy $\left( {\Delta \overline G_{\rm{m}}^{*}} \right)$ as the overpotential (η) is increased.

Expanding Eq. 6.37 yields

$$ \Delta \overline G_{\rm{m}}^{*} = \frac{{\lambda_{\rm{m}}^2 - 2{\lambda_{\rm{m}}}F\eta + {F^2}{\eta^2}}}{{4{\lambda_{\rm{m}}}}} $$

(6.41)

which rearranges into the form

$$ \Delta \overline G_{\rm{m}}^{*} = \frac{{{\lambda_{\rm{m}}}}}{4} - \left( {\frac{{2\beta + 1}}{4}} \right)F\eta $$

(6.42)

Now substituting back into Eq. 6.38 yields

$$ {k_{\rm{et}}} = \frac{{2\pi }}{\hbar }{\left| {{{H\prime}_{\rm{DA}}}} \right|^2}\frac{{{N_{\rm{A}}}}}{{\sqrt {{4\pi \,{\lambda_{\rm{m}}}RT}} }}\exp \left( {\frac{{ - {\lambda_{\rm{m}}}}}{{4RT}}} \right)\exp \left( {\frac{{\left( {{2}\beta + 1} \right)F\eta }}{{4RT}}} \right) $$

(6.43)

$$ {k_{\rm{et}}} = {k_0}\exp \left( {\frac{{\left( {{2}\beta + 1} \right)F\eta }}{{4RT}}} \right) $$

(6.44)

where the parameter k ₀ is a complicated function of temperature T but is independent of overpotential η. An analogous equation applies to the back reaction, except that β is replaced by (1 − β). Thus, for the overall current–voltage curve, we may write

$$ I = {I_0}\left\{ {\exp \left( {\frac{{\left( {2\beta + 1} \right)F\eta }}{{{4}RT}}} \right) - \exp \left( {\frac{{ - \left( {3 - 2\beta } \right)F\eta }}{{{4}RT}}} \right)} \right\} $$

(6.45)

where

$$ \beta = \frac{1}{2}\left( {1 - \frac{{F\eta }}{{{\lambda_{\rm{m}}}}}} \right) $$

(6.46)

Equation 6.45 may be compared directly with experimental data. However, it should not be forgotten that I ₀ and β are both functions of temperature T. (In the case of β, via the dependence of λ _m on T.) Thus, the temperature should be measured and, preferably, controlled.

Equation 6.45 is the current–voltage curve for a reversible, one-electron transfer reaction at thermal equilibrium. It differs from the “textbook” Butler–Volmer equation [83, 84] namely

$$ I = {I_0}\left\{ {\exp \left( {\frac{{{\beta_{\rm{f}}}F\eta }}{{RT}}} \right) - \exp \left( {\frac{{ - {\beta_{\rm{b}}}F\eta }}{{RT}}} \right)} \right\} $$

(6.47)

because the latter was derived on the basis of a different definition of the symmetry factor. However, the models can be reconciled via the following transformation formulas:

$$ {\beta_{\rm{f}}} = \frac{{2\beta + 1}}{4} $$

(6.48)

and

$$ {\beta_{\rm{b}}} = \frac{{3 - 2\beta }}{4} $$

(6.49)

so that

$$ {\beta_{\rm{f}}} = \frac{1}{2}\left( {1 - \frac{{F\eta }}{{{2}{\lambda_{\rm{m}}}}}} \right) $$

(6.50)

and

$$ {\beta_{\rm{b}}} = \frac{1}{2}\left( {1 + \frac{{F\eta }}{{{2}{\lambda_{\rm{m}}}}}} \right) $$

(6.51)

It is unfortunate (and not widely realized) that the symmetry factor that is used in electron transfer theory is not the same as the symmetry factor that is used in electrochemistry textbooks. However, for avoidance of ambiguity, we shall hereafter use only the “electrochemistry” parameters β _f and β _b.

Tafel slopes for multistep reactions

As shown above, the current–voltage curve for a reversible, one-electron transfer reaction at thermal equilibrium may be written in the form

$$ I = FAC{k_0}\left\{ {\exp \left( {\frac{{{\beta_{\rm{f}}}F\eta }}{{RT}}} \right) - \exp \left( {\frac{{ - {\beta_{\rm{b}}}F\eta }}{{RT}}} \right)} \right\} $$

(6.52)

which corresponds to the reaction

$$ {\hbox{A + }}{{\hbox{e}}^{-} } \leftrightarrows {\hbox{B}} $$

(6.53)

In what follows, we seek to derive the current–voltage curves corresponding to the more complex reaction

$$ {\hbox{A + }}n{{\hbox{e}}^{-} } \leftrightarrows Z $$

(6.54)

For simplicity, we consider the forward and backward parts of the rate-determining step independently. This makes the rate-determining step appear irreversible in both directions. The general approach is due to Roger Parsons [85].

We begin by writing down all the electron transfer reactions steps separately:

(6.55)

Next, we adopt some simplifying notation. First, we define n _p to be the number of electrons transferred prior to the rate-determining step. Then, we define n _r to be the number of electrons transferred after the rate-determining step. In between, we define n _q to be the number of electrons transferred during one elementary act of the rate-determining step. (This is a ploy to ensure that n _q can take only the values 0 or 1, depending on whether the rate-determining step is a chemical reaction or an electron transfer. This will be convenient later.)

Restricting attention to the above system of unimolecular steps, the total number of electrons transferred is

$$ n = {n_{\rm{p}}} + {n_{\rm{q}}} + {n_{\rm{r}}} $$

(6.56)

We now make the following further assumptions. (1) The exchange current of the rate-determining step is at least 100 times less than that of any other step; (2) the rate-determining step of the forward reaction is also the rate-determining step of the backward reaction; (3) no steps are concerted; (4) there is no electrode blockage by adsorbed species; and (5) the reaction is in a steady state. Given these assumptions, the rate of the overall reaction is

$$ \begin{array}{*{20}{c}} {{I_{\rm{total}}}} & { = {I_0}\left[ {\exp \left( {\left[ {{n_{\rm{p}}} + {n_{\rm{q}}}{\beta_{\rm{f}}}} \right]\frac{F}{{RT}}\eta } \right) - \exp \left( { - \left[ {{n_{\rm{r}}} + {n_{\rm{q}}}{\beta_{\rm{b}}}} \right]\frac{F}{{RT}}\eta } \right)} \right]} \\{} & { = {I_0}\left[ {\exp \left( {{{{\alpha_{\rm{f}}}F\eta } \mathord{\left/{\vphantom {{{\alpha_{\rm{f}}}F\eta } {RT}}} \right.} {RT}}} \right) - \exp \left( {{{ - {\alpha_{\rm{b}}}F\eta } \mathord{\left/{\vphantom {{ - {\alpha_{\rm{b}}}F\eta } {RT}}} \right.} {RT}}} \right)} \right]} \\\end{array} $$

(6.57)

In the above expression, α _f should properly be called the transfer coefficient of the overall forward reaction, and correspondingly α _b should properly be called the transfer coefficient of the overall backward reaction. But in the literature, they are often simply called transfer coefficients.

It may be observed that n _r does not appear inside the first exponential in Eq. 6.57. This is because electrons that are transferred after the rate-determining step serve only to multiply the height of the current/overpotential relation and do not have any effect on the shape of the current/overpotential relation. For the same reason, n _p does not appear inside the second exponential in Eq. 6.57.

Although Eq. 6.57 has the same outward form as the Butler–Volmer equation (Eq. 6.47), actually the transfer coefficients α _f and α _b are very different to the modified symmetry factors β _f and β _b and should never be confused with them. Basically, α _f and α _b are composite terms describing the overall kinetics of multistep many-electron reactions, whereas β _f and β _b are fundamental terms describing the rate-determining step of a single-electron transfer reaction. Under the assumptions listed above, they are related by the equations

$$ {\alpha_{\rm{f}}} = {n_{\rm{p}}} + {n_{\rm{q}}}{\beta_{\rm{f}}} $$

(6.58)

and

$$ {\alpha_{\rm{b}}} = {n_{\rm{r}}} + {n_{\rm{q}}}{\beta_{\rm{b}}} $$

(6.59)

A century of electrochemical research is condensed into these equations. And the key result is this: if the rate-determining step is a purely chemical step (i.e., does not involve electron transfer), then n _q = 0 and the modified symmetry factors β _f and β _b disappear from the equations for α _f and α _b. Conversely, if the rate-determining step is an electrochemical step (i.e., does involve electron transfer), then n _q = 1 and the modified symmetry factors β _f and β _b enter the equations for α _f and α _b.

Remark

α_f and α_b differ from β_f and β_b in another important respect. The sum of β_f and β_b is

$$ {\beta_{\rm{f}}} + {\beta_{\rm{b}}} = 1 $$

(6.60)

whereas the sum of α_f and α_b is

$$ {\alpha_{\rm{f}}} + {\alpha_{\rm{b}}} = n $$

(6.61)

That is, the sum of the transfer coefficients of the forward and backward reactions is not necessarily unity. This stands in marked contrast to the classic case of a single-step one-electron transfer reaction, for which the sum is always unity. Furthermore, in systems where the rate-determining steps of the forward and backward reactions are not the same—a common occurrence—the sums of α _f and α _b have no particular diagnostic value. Experimentally, it is traditional to determine the values of α _f and α _b by evaluating the expression

$$ \frac{{\partial \eta }}{{\partial \,{ \log }\left| I \right|}} = \frac{{2.303RT}}{{{\alpha_{\rm{f}}}F}} = b $$

(6.62)

where b is called the “Tafel slope” [86]. Some theoretical values of b for multistep electrochemical reactions [87], derived via Eq. 6.58, are listed in Table 8.

Table 8 Tafel slopes for multistep electrochemical reactions

In order to simplify the data in the table, we have assumed 2.303RT/F ≈ 60 mV at 25 °C. (Actually, the precise value is 59.2 mV.) We have also written β _f in the form

$$ {\beta_{\rm{f}}} = \frac{1}{2}\left( {1 - \frac{{F\eta }}{{{2}{\lambda_{\rm{m}}}}}} \right) = {\raise0.7ex\hbox{$1$} \!\mathord{\left/{\vphantom {1 2}}\right.}\!\lower0.7ex\hbox{$2$}}\left( {1 - \Delta } \right) $$

(6.63)

Although most of the tabulated Tafel slopes have been derived previously, it is interesting to see them compiled in one list because it emphasizes their shared assumptions. Some of these are:

• 1. The ambient solution is at thermodynamic equilibrium.

• 2. All reaction steps are at thermodynamic equilibrium, except the rate-determining step.

• 3. There is weak orbital overlap between the electrode and the acceptor species.

• 4. The acceptor species experience Gaussian fluctuations of energy.

The effects of weakening these assumptions are not well cataloged, either theoretically or experimentally.

Conclusions

The investigation of electron transfer reactions presents problems of remarkable difficulty and complexity. Traditionally, the theory has been modeled at various levels, both quantum and classical, and it is not very easy to see how the results are connected. There are also problems of scale. Recently, more than 20,000 research papers related to electron transfer have become accessible via the internet, and more than 1.5 million web pages. Given this torrent of information, the development of a satisfactory synthesis of theory and experiment is still very much a “work in progress.” The history of electron transfer has yet to be written.

Throughout the compilation of the present document, much effort was expended in identifying the most original ideas from the past century and placing them in a common mathematical framework. Some interesting generalizations emerged from this process. Perhaps the most intriguing was the discovery that electron transfer could be triggered by two fundamentally different phenomena—mechanical distortions or charge fluctuations. These possibilities may be used to replace the earlier categorizations of inner-sphere and outer-sphere kinetics, to which they roughly correspond, though not exactly. Assuredly, the inner-sphere contribution to the activation energy is usually due to mechanical distortions, and the outer-sphere contribution is usually due to charge fluctuations, but there is actually no fundamental reason why this should be a universal truth. In many systems, it is surely the case that there are mechanical distortions in the outer sphere or charge fluctuations in the inner sphere or both, and these possibilities should now be considered.

The present work also sheds light on the literature confusion between Gibbs energy diagrams and potential energy diagrams. A Gibbs energy diagram is appropriate for thermally activated reactions. In such cases, the reactive species continually and randomly exchange heat with the environment (the heat bath), and therefore they move randomly up and down both sides of the Gibbs energy parabola. By contrast, the potential energy diagram is appropriate for situations in which the reactive species do not exchange heat with the environment, so that they are essentially isolated. In these cases, the reactive species conserve energy by transferring it between potential energy states and kinetic energy states, in the manner of an oscillator.

Limited space in the final document compelled some difficult choices. After much deliberation, I decided to omit discussion of proton tunneling, superexchange, and scanning tunneling microscopy. These are, of course, important topics, but they represent elaborations of the core theory, rather than being core theory per se. Thankfully, the choice of experimental data was a little easier. The data listed in the tables and figures are all derived from rare, and in many cases unique, experiments in which the effects of fundamental variables were unambiguously determined. One can only marvel at the skill of the original researchers. To this day, it remains a source of deep frustration that the fundamental variables of electron transfer theory (such as the orbital overlap and the density of energy states) are so difficult to control experimentally.

Much recent research has been directed towards molecular electronics. This is a rapidly develo** field that typically involves electron transfer between two metal electrodes separated by a single molecule. Numerous studies have indicated that the rates of reaction are dominated by contributions from non-Fermi energies in the metals. However, the theory is new and largely untested, and that is why I have not reviewed it in the present work. For further information, the reader is referred to the recent paper of Zhang et al. [88].

In the present work, an interesting distinction has emerged between the charge fluctuation model and the solvent fluctuation model. In the normal range of electron transfer, on the charge fluctuation model, the reorganization energy λ has the value [22]

$$ \lambda = \frac{1}{2}{e^2}\left( {\frac{1}{{4\pi {\varepsilon_0}}}} \right)\left( {\frac{1}{{\varepsilon \left( \infty \right)}}} \right)\left( {\frac{1}{{{a_{\rm{D}}}}} + \frac{1}{{{a_{\rm{A}}}}} - \frac{2}{d}} \right) $$

(7.1)

where −e is the charge on the electron; ε ₀ is the permittivity of free space; ε(∞) is the relative permittivity (dielectric constant) of the solution in the high frequency limit; a _D is the radius of the donor supermolecule; a _A is the radius of the acceptor supermolecule; and d is the center-to-center distance between the supermolecules. In general, the radius of each supermolecule consists of three terms—(1) the ionic radius, (2) the thickness of the compact layer (a constant independent of concentration of supporting electrolyte), and (3) the thickness of the diffuse layer (a variable that depends on the ionic strength of supporting electrolyte). By contrast, on the solvent fluctuation model, the reorganization energy λ has the value [54]

$$ \lambda = \frac{1}{2}{e^2}\left( {\frac{1}{{4\pi {\varepsilon_0}}}} \right)\left( {\frac{1}{{\varepsilon \left( \infty \right)}} - \frac{1}{{\varepsilon \left( {0} \right)}}} \right)\left( {\frac{1}{{{r_{\rm{D}}}}} + \frac{1}{{{r_{\rm{A}}}}} - \frac{2}{d}} \right) $$

(7.2)

where −e is the charge on the electron; ε ₀ is the permittivity of free space; ε(∞) is the relative permittivity (dielectric constant) in the high frequency limit; ε(0) is the relative permittivity (dielectric constant) in the low frequency limit; r _D is the radius of the donor molecule (including any inner coordination shell); and r _A is the radius of the acceptor molecule (including any inner coordination shell). It is immediately clear that Eq. 7.2 does not take ionic strength into account, whereas Eq. 7.1 does.

Combination of Eq. 6.22 with Eqs. 5.16 and 5.17 yields the new result

$$ {k_{\rm{et}}} = \frac{{2\pi }}{\hbar }{\left| {H\prime} \right|^2}S_{\rm{DA}}^2\frac{1}{{\sqrt {{4\pi \lambda \,{k_{\rm{B}}}T}} }}\exp \left( {\frac{{ - {{\left( {\lambda + \Delta {G^0}} \right)}^2}}}{{4\lambda \,{k_{\rm{B}}}T}}} \right) $$

(7.3)

where H′ is a constant and S _DA is the extent of overlap between the donor and the acceptor orbitals (i.e., the overlap integral). This expression is, I think, more transparent than the usual golden rule formulation because it makes explicit the need for orbital overlap (and constructive interference) between the donor and the acceptor species.

Finally, regarding an experimental test of the three primary theories of the reaction coordinate (Randles, Fletcher, Marcus), perhaps the most telling differences between them may be found in their vastly different predictions regarding changes in the relative permittivity (dielectric constant) of the solvent. The Randles “bond-stretching” model suggests that electron transfer to a specified complex ion should be essentially independent of solvent polarity. By contrast, the Fletcher “charge fluctuation” model suggests that electron transfer should be strongly catalyzed by polar solvents in the inverted and superverted regions. Finally, the Marcus “dielectric fluctuation” model suggests that electron transfer should be strongly inhibited by polar solvents (such as water) and strongly catalyzed by nonpolar solvents (such as carbon tetrachloride) in all regions of driving force. Given these differences, what is now needed is an experimentum crucis in which the relative permittivity (dielectric constant) of the solvent is treated as an experimental variable. That remains a tantalizing goal for the twenty-first century.