Semi-analytical findings for rotational trapped motion of satellite in the vicinity of collinear points {L₁, L₂} in planar ER3BP

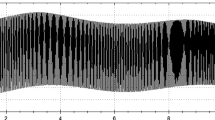
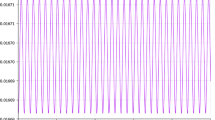
Abstract

A novel approach for solving equations of the rotational dynamics of finite-sized satellite in the vicinity of collinear points {L₁, L₂} for the elliptic restricted problem of three bodies, ER3BP is presented in this work. We consider two primaries, M_Sun and m_planet (the last is secondary in that binary system), both are orbiting around their barycenter on elliptic orbits. Case of collinear point L₃ should be investigated additionally in future works. Our aim is to revisit previously presented in work (Ashenberg: J Guid Control Dyn 19(1):68–74, 1996) approach and to investigate the updated type of the dynamics of satellite rotation correlated implicitly to its motion (in the synodic co-rotating Cartesian coordinate system) in so way that it will always be located near the secondary planet, m_planet, moving in this motion in the vicinity of collinear points {L₁, L₂} on quasi-stable elliptic orbit.

Appendix: A1 (estimation of absolute magnitudes for parameter A in (5)–(8))

Let us estimate the absolute magnitudes of parameter A which have been presented in formulae (5)–(8) [e.g. for the expression presented in the left part of (8)] by series of Taylor expansions, neglecting the terms of second-order smallness and less:

$$ \mu \; < < \;1\quad \Rightarrow A\; = \;\left( {\frac{1}{2}\sqrt {1 + 3(1 - 2\mu )^{{{\kern 1pt} 2}} } } \right)\omega_{{{\kern 1pt} 0}}^{2} \; \cong \left( {\sqrt {1 - 3\mu } } \right)\omega_{0}^{2} \; \cong \left( {1 - \frac{3\mu }{2}} \right){\kern 1pt} {\kern 1pt} \omega_{0}^{2} $$

where ω₀² = 3(B − A)/C <  < 1 is the inertial parameter of the satellite (which equals to zero for ellipsoid of rotation, for example), whereas e.g. $\mu \; \cong \;3.040 \cdot 10^{{\, - {\kern 1pt} 6}}$ for the case of two primaries in system “Earth-Sun”.

It is worth to note that the range of possible initial values for α is limited as pointed below:

$$ (5)\quad \Rightarrow \quad \left( {\frac{{{\text{d}}\alpha }}{{{\text{d}}t}}} \right)^{{{\kern 1pt} 2}} = \left( {\left. {\frac{{{\text{d}}\alpha }}{{{\text{d}}t}}} \right|_{t = 0} } \right)^{{{\kern 1pt} 2}} + B\alpha - \left( \frac{A}{2} \right)\,(\cos \,2\alpha - 1)\quad \Rightarrow \quad B\alpha_{{{\kern 1pt} 0}} = - A\sin^{2} \alpha_{0} $$

(9)

$$ \left\{ {B = (4e\,\sin \,f)\,,\;A = - \;\left[ {\frac{1 - \mu }{{r_{1}^{3} }} + \frac{\mu }{{r_{2}^{3} }}} \right]{\kern 1pt} {\kern 1pt} \omega_{{{\kern 1pt} 0}}^{2} \le 0\;} \right\} $$

Namely, the only possible initial value (for wide range of true anomaly f) is, obviously, α₀ = 0.