Abstract
There is a new nature-inspired algorithm called salp swarm algorithm (SSA), due to its simple framework, it has been widely used in many fields. But when handling some complicated optimization problems, especially the multimodal and high-dimensional optimization problems, SSA will probably have difficulties in convergence performance or drop** into the local optimum. To mitigate these problems, this paper presents a chaotic SSA with differential evolution (CDESSA). In the proposed framework, chaotic initialization and differential evolution are introduced to enrich the convergence speed and accuracy of SSA. Chaotic initialization is utilized to produce a better initial population aim at locating a better global optimal. At the same time, differential evolution is used to build up the search capability of each agent and improve the sense of balance of global search and intensification of SSA. These mechanisms collaborate to boost SSA in accelerating convergence activity. Finally, a series of experiments are carried out to test the performance of CDESSA. Firstly, IEEE CEC2014 competition fuctions are adopted to evaluate the ability of CDESSA in working out the real-parameter optimization problems. The proposed CDESSA is adopted to deal with feature selection (FS) problems, then five constrained engineering optimization problems are also adopted to evaluate the property of CDESSA in dealing with real engineering scenarios. Experimental results reveal that the proposed CDESSA method performs significantly better than the original SSA and other compared methods.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
It is generally known that population-based optimization algorithms can find high-quality solutions based on random operations [1,2,3,4,5, 112,113,114,115,116]. Being a new population optimizer, the salp swarm algorithm (SSA) [6] was created by Mirjalili in 2017. In literature [6], it can be found that SSA is superior to well-known algorithms: harmony search (HS) [7], particle swarm optimization (PSO) [8], gravitational search algorithm (GSA) [9], and flower pollination algorithm (FPA) [10] on CEC-BBOB-2015 test functions, and the multi-objective SSA (MSSA) outperforms the classical multi-objective algorithms: multiobjective particle swarm optimization (MOPSO) [11] and multiobjective evolutionary algorithm based on decomposition (MOEA/D) [12] on IEEE CEC2009 test suits, meanwhile, SSA and MSSA have been used to deal with seven engineering optimization problems. As a swarm algorithm, it has a high potential to approximate the optimal solutions with a satisfying convergence rate and coverage of solution space. In addition, it is much easier to comprehend and implement due to its simple mathematical model and framework. So it has been employed frequently to realize many real-world requests, for instance, feature selection (FS), energy, and environmental protection [13,14,15]. Lately, Faris et al. have summarized the work on SSA and they adopted it to train extreme learning machine (ELM) significantly [16].
One of the most crucial applications of SSA is FS. Faris et al.[17] built a binary SSA integrating a crossover scheme to deal with FS; 22 well-known UCI datasets tested its performance. Sayed et al. [18] presented a hybrid algorithm by embedding chaos theory into SSA. Mohammad et al. [19] integrated singer chaotic map and a new local search algorithm (LSA) into SSA for FS. Although all the experiment results clearly show that SSA shows promising performance in dealing with FS, the improved SSA variants are aimed at specific datasets. We see they perform badly on some datasets, so the algorithms need to be enhanced further and expand the field of application.
Another critical application of SSA is parameter estimation and result forecast. El-Fergany [20] presented an SSA-based method to evaluate parameters of polymer exchange membrane fuel cells (PEMFCs) to guarantee cognitive modeling, simulation, and control. Zhang et al. [21] applied SSA in parameter estimation for the soil water retention curve. Hussien et al. [22] introduced a K-nearest neighbor (KNN) to SSA for predicting chemical compound activities. Zhao et al. [23] established a novel model named SSA-LSSVM for CO2 prediction; SSA was used to optimize two parameters in the least-squares support vector machine (LSSVM). Although SSA variants get better results in dealing with parameter identification and result forecast problems, due to the model’s performance depends on the given datasets, the precision needs to be further enhanced to be hired in the real application fields.
The SSA was also employed to tackle and recognize solutions to other engineering optimization. Ateya et al. [24] used chaotic maps to enhance SSA and applied it to optimize controllers’ numbers and connections between switches and controllers in large scale SDN networks. Yang et al. [25] proposed a memetic SSA (MSSA) for the PV systems in the condition of partial shading. Wang et al. [26] introduced bound estimation into multi-objective SSA to deal with short-term load forecasting problems. Abbassi et al. [27] utilized an SSA-based strategy to obtain the optimal configurations of photovoltaic cell models. Abadi et al. [28] combined SSA and genetic algorithm (GA) for nurses’ scheduling and designation in COVID-19 pandemic. Salma et al. [29] adopted both a random mutation operator and an adaptive process to boost the search capability of SSA for solving optimal power flow (OPF) problems. Ewees et al. [30] combined firefly algorithm (FA) with SSA to deal with unrelated parallel machine scheduling problems (UPMSP). Rohit et al. [31] brought the self-adaptive parameters strategy in SSA to boost its convergence performance. Although SSA gets better results in solving real engineering optimization problems, we see the accuracy and efficiency requires to be augmented for satisfying actual needs.
It is observed that the SSA performs better in solving a lot of optimization problems. However, it needs to be improved in terms of convergence precision and rate in dealing with complex optimization problems. A range of scholars applied different local and global search enhanced mechanisms to boost its exploration and exploitation drifts. Ibrahim et al. [32] combined the characteristic of SSA with the feature of PSO, which is named SSAPSO, to improve the global and local search capability of basic SSA. In this framework, if the random value is bigger than 0.5, the SSA’s mechanisms are adopted. Otherwise, PSO’s mechanisms are applied; they reported that the SSAPSO is better than the simple SSA in dealing with 15 benchmark functions. Furthermore, the SSAPSO is employed to deal with FS problems on the UCI datasets. Rizk-Allah et al. [33] presented five versions of binary SSA with different transformations, and they all have been tested on 18 benchmark functions. The results show that the binary SSA embedding a modified Arctan transformation called BBSA-V has competitive performance. Divya et al. [34] embedded random opposition-based learning, multiple leadership, and simulated annealing into SSA to enhance its performance in solving complex multi-modal problems. Malik et al. [35] employed a novel lifetime scheme to accelerate the convergence performance of SSA. Bhaskar et al. [36] employed Gaussian, Cauchy, and levy-flight mutation schemes to enhance the performance of SSA. Fatima et al. [37] introduced the local best information and differential evolution to improve SSA named MSSA. Nibedan et al. [38] adopted both normal distributed mutation operator and oppositional learning concept to enhance the performance of SSA. Ren et al. [39] used the random replacement strategy and double adaptive weight to improve the performance of SSA. Saafan et al. [40] integrated improved whale optimization algorithm (IWOA) into SSA to boost its performance. Although the above mechanisms have enhanced SSA comparatively, these strategies are usually for the given problems, at the same time the convergence precision and rate of the process requires to be still enhanced.
As mentioned above, though many scholars have done a lot of valuable efforts to improve the property of SSA, we observe its exploitation and exploration propensities need to be further improved. As we experienced, the chaotic map has a good random performance, so it is usually utilized in improving the algorithm’s parameters, intensification, and the initialization of the population. Zhang et al. [14] proposed a new SSA variant named CMSSA, three mechanisms: Gaussian mutation, Cauchy mutation, and chaotic exploitative mechanism (CEM) were combing with SSA to boost its performance. The results verify that CMSSA is better than PSO with an aging leader and challengers (ALCPSO) [41], comprehensive learning particle swarm optimizer (CLPSO) [42], self-adaptive differential evolution (SaDE) [43], jDE [44], hybridizing grey wolf optimization (HGWO) [45], and improved grasshopper optimization algorithm (IGOA) [46] on 23 well-known benchmark functions. Emre et al. [47] used a chaotic map to update the control parameter, mutualistic relationship to enhance search performance, and a random technique to enhance the diversity. Liu et al. [48] integrated the chaotic exploitative trends and multi-population structure to enhance the performance of SSA. DE method has a superior searching performance, and it has widely been used to uphold the performance of other algorithms. Rohit et al. [49] adopted the mutation operators to boost the performance of SSA. Zhang et al. [50] combined the improved mutation operation of DE and restart mechanism with SSA to improve its optimization performance.
In this paper, a chaotic SSA with DE (CDESSA) is proposed by adopting chaotic initialization and DE-based mechanisms to help the SSA jump out of the local optimum (LO) and accelerate its convergence rapidity too. As far as we know, these strategies are firstly utilized to advance the effectiveness of SSA regarding exploratory and exploitative drifts. This paper has contributions as follow:
-
For one aspect, chaotic initialization is utilized to provide a better initial population; it is conducive to finding better global optima (GO).
-
In another aspect, DE is employed to boost the searching capability of each individual to increase the convergence potential and convergence accuracy of SSA.
-
Chaotic initialization and DE can help the exploration and exploitation competencies of SSA to make a more suitable balance.
-
We provide an efficient solver, called the CDESSA, to deal with functions of IEEE CEC2014, FS problems, constrained engineering optimization to not only solve high-dimensional and multimodal problems but also deal with complex practical application problems.
This work is conducted as below: The basic theory of original SSA was elaborated in Sect. 2. The proposed CDESSA was described in detail in Sect. 3. The experiment results and discussions were explained in Sect. 4. At last, the conclusions and future research plans were given briefly in Sect. 5.
2 Salp swarm algorithm (SSA)
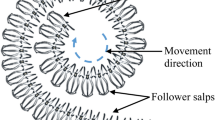
SSA is a bio-inspired optimizer firstly established by Mirjalili in 2017 [6], which is inspired by the swarming activities of salps when they are navigating and foraging for foods in oceans. Interestingly, salps often come together in a chain. This phenomenon can be illustrated in Fig. 1. Though this phenomenon cannot be interpreted by the theory, this interesting phenomenon can be ascribed to gain better movement through both rapid cooperation movement and foraging by Anderson [51].
To establish a mathematical model for the swarm, the salp swarm is divided into two groups: the leader and followers. The salp in the first place of the chain is called leader, so the rest of the salps are treated as followers. Taken literally, the leader leads the direction of the swarm, and the followers follow the leader one after another.
Like other swarm optimizers, the location of salps is defined as a D-dimensional vector where D is the dimension of the given problem. Hence, the position of all salps forms a two-dimension matrix called X. It is also supposed that the food source called F in the search space is the foraging target of the swarm. The following equation updates the position of the leader:
where \(X_{1,j}\) shows the position of leader in the jth dimension, Fj is the position of the food source in the jth dimension, ubj denotes the jth dimension of the upper bound, lbj indicates the jth dimension of lower bound, c1, c2, and c3 are control parameters.
The rule in Eq. (1) shows that the position of the leader is updated only based on the food source. The parameters c2 and c3 are random real numbers that are uniformly generated in the region of [0,1]. The most critical parameter c1 used to keep the poise between exploration and exploitation drifts in SSA is calculated as follows:
where l means current iteration, meanwhile, L is the maximum iteration.
The location of followers is renewed ed by:
where \(X_{i,j}\) means the location of the ith follower salp in the jth dimension.
The flowchart of SSA is demonstrated in Fig. 2. The implemented process of SSA can be depicted as the below steps:
Step 1: Produce the initial salp population randomly within the boundaries of the solution space and evaluate the population and gain the best salp, as the global best solution (FoodPosition), and attain its fitness (FoodFitness), l = 1.
Step 2: If the current iteration l is not more than the maximum iteration L, go to Step 3; otherwise, go to Step 6.
Step 3: Update the parameter c1 according to Eq. (2).
Step 4: if i == 1, replace the location of the leading salp based on Eq. (1); else renew the location of the follower salp based on Eq. (3).
Step 5: Amend the salps according to the upper and lower boundaries of the problem, and evaluate the salp population, if the best salp in the current population is better than the global best solution (FoodPosition), then, update the global best solution (FoodPosition) by the best salp in the current population; otherwise, the global best solution (FoodPosition) keeps unchanged, l = l + 1, and go to Step 2.
Step 6: Return the best solution (FoodPosition) and its fitness (FoodFitness).
3 Proposed chaotic SSA with DE (CDESSA)
The original SSA has some advantages such as quick convergence speed and simple structure. However, when solving more complicated practical optimization problems, it may easily face stagnation problems. The performance of SSA mainly depends on the interactions between the leader agent and follower agents. When a single agent falls into the LO, the agent can jump out of the LO by the full effect of the leading agent. But if most agents sink into the same condition, the whole algorithm will slow down and lock down around the LO finally. This condition provides the opportunity for other strategies to be embedded in SSA, so the performance of SSA will be improved.
3.1 Chaotic initialization mechanism
Literature [52, 53] has pointed out that a well-distributed initial population is always useful. For instance, it will assist the population to converge to a better optimal solution, and it may also augment the convergence speed and quickness of the optimization process. The chaotic map has been widely utilized throughout the initialization period of the optimizers due to the following characteristics: closeness to the initial condition, semi-randomness, and ergodicity. In the initialization phase, for one aspect, the chaotic map is utilized to produce random parameters to replace the uniform or gaussian parameters [54,55,56]. For another aspect, the chaotic map is adopted to generate a chaotic solution [57,58,59], as well as the role of opposition-based learning [60].
In this paper, the logistic map is exploited to generate a chaotic solution of the agent in the initialization; the distribution of the logistic map can be denoted by Eq. (4).
where \(\mu\) is coefficient, it is often equal to 4, at this time chaotic map will be produced; \(t\) is the index of current chaotic number; \(N\) is population size; \(C\left( 1 \right)\) indicates a random number in the range \(\left( {0, 1} \right)\) that is not equal to 0.25, 0.5, and 0.75; \(N - 1\) chaotic numbers will be generated based on Eq. (4).
The chaotic solution of the ith agent can be attained by Eq. (5).
where \(C\left( t \right)\) is the tth chaotic numbers; \(X_{i}\) denotes the ith agent; \(CX_{i}\) indicates the chaotic solution of the ith agent.
3.2 Differential evolution mechanism
The DE algorithm is a population-based algorithm and it has been embedded into many optimizers [61, 117]. Its optimization process mainly includes mutation, crossover, and selection, in which mutation is the key factor of DE; it determines the optimization adaptation of DE mainly. Aim to prevent SSA from drop** into premature convergence. The well-known DE is introduced into SSA to generate a new, better candidate solution for each search agent as an intensification tool. The population has \(N\) search agents. Each agent is a vector with \(D\) dimensions denoted as \(X_{i} = \left( {X_{i,1} ,X_{i,2} , \ldots ,X_{i,D} } \right)\).
3.2.1 Mutation
In the mutation process, the mutation operator is carried out by selecting three diverse agents \(X_{r1}\), \(X_{r2}\), and \(X_{r3}\) from the current population, where \(r1 \ne r2 \ne r3 \ne i\), so a mutant vector \(U_{i}\) can be attained. The mutation operator can be denoted as Eq. (6).
where \(F\) is the mutation scale factor, it is a vector of \(D\) dimensions. Each dimension distributes in the range \(\left[ {0, 1} \right]\).
In this study, mutation scale factor \(F\) can be generated by Eq. (7).
where \(U\) stands for uniform distribution, it means generating a vector \(F\) with \(D\) dimensions. Each dimension is uniformly distributed in the range \(\left[ {F_{\min } , F_{\max } } \right]\). In this paper, \(F_{\min } = 0.2\) and \(F_{\max } = 0.8\).
3.2.2 Crossover
In this process, a trial vector \(V_{i}\) can be generated by carrying out a crossover operator. The crossover operator can be modeled as Eq. (8):
where \(P_{{{\text{CR}}}}\) is a probability factor in determining the diversity of the swarm and prevents the algorithm from dwindling into local minima. In this paper, \(P_{CR} = 0.1\). \({\text{rand}}\) is a random number in the range \(\left[ {0, 1} \right]\)., \(j_{{{\text{rand}}}}\) is an index, which is randomly generated between \(\left\{ {1, 2, \ldots , D} \right\}\). It ensures that one element of the trial vector \(V_{i}\) comes from mutant vector \(U_{i}\).
3.2.3 Selection
Selection operator means that the better offspring is chosen between the trial vector \(V_{i}\) and the search agent \(X_{i}\) based on fitness. It can guarantee that the better candidate solution will be retained, so the convergence speed and accuracy of the algorithm will be enhanced. This operator can be denoted as Eq. (9):
3.3 The implementation of CDESSA
The implementation details of CDESSA are introduced in this section. In the original SSA, the search agent moves to the next location based on the leader agent or its previous agent; therefore, a promising solution cannot always be obtained in each time so that the algorithm will trap into early convergence; its convergence speed and accuracy will be prevented to be further improved. To further develop the exploitation and exploration trends of SSA, chaotic initialization mechanism and DE-based mechanism are combined with SSA to form a new enhanced SSA, named CDESSA.
In CDESSA, a chaotic initialization mechanism is utilized to build a better opening population for the subsequent optimization process. Because the quality of the initial population regulates the convergence rapidity and accuracy of the population-based algorithms, a chaotic initialization mechanism guarantees that we keep an initial population as random as possible. This gives the algorithm more chance to escape from the LO and find a more promising solution. A DE-based mechanism is utilized to intensify the exploitation and exploration of the search agent as an intensification technique. This gives the search agents more opportunities to find a more satisfactory solution. Hence, the convergence speed and accuracy of the algorithm will be further enhanced.
The flowchart of CDESSA is shown in Fig. 3. The implemented process of the CDESSA method can be depicted as below:
Step 1: Generate the location of the search agent in the initial population randomly by Eq. (10), \({\text{FEs}} = {\text{FEs}} + N\).
where \(X_{i,j}\) means the jth dimension of the position of the ith agent; \(lb_{j}\) and \(ub_{j}\) denote the jth dimension of the lower bound and upper bound, respectively; \({\text{rand}}()\) produces a random number in the range.
Step 2: Evaluate the fitness of each individual in the initial population; calculate the chaotic solution of the individual in the initial population by Eqs. (4) and (5), thus, the \(N\) chaotic solutions can be obtained and form a chaotic population; choose the best \(N\) solutions from both the initial population and the chaotic population to update the initial population, repeat this process \(N - 1\) times and obtain the best initial population to participate in the next iteration process; get the optimal solution (FoodPosition), \({\text{FEs}} = {\text{FEs}} + \left( {N - 1} \right) \times N\).
Step 3: Initialize the algorithm parameters such as \(c_{1}\), \(F_{\min }\), \(F_{\max }\), \(P_{{{\text{CR}}}}\), in which \(c_{1}\) can be generated by Eq. (11):
where \({\text{FEs}}\) is the current fitness evolution number; \({\text{MaxFEs}}\) is the maximum fitness evolution number.
Step 4: If \(i = = 1\), refresh the location of the leader agent by Eq. (1); else renew the location of the follower agents by Eq. (3).
Step 5: Select three different agents from the current population, then carry out a DE mechanism and generate the candidate solution of the search agent by Eqs. (6), (7), (8), update the search agent by Eq. (9), \({\text{FEs}} = {\text{FEs}} + N\).
Step 6: Amend the position of the agent within the lower and upper bound, evaluate the fitness of each agent in the current population, \({\text{FEs}} = {\text{FEs}} + N\); if the optimal agent is better than the global optimal solution (FoodPosition), update the global optimal solution (FoodPosition) by the optimal agent in the current population; else the global optimal solution (FoodPosition) keeps unchanged.
Step 7: If the termination condition is met (\({\text{FEs}} < {\text{MaxFEs}}\)), repeat Steps 4–6; otherwise, go to Step 8.
Step 8: Output the global optimal solution (FoodPosition) and its fitness (FoodFitness).
3.4 The time complexity of CDESSA
The proposed algorithm is made of chaotic initialization mechanism, DE mechanism, and basic SSA, so its computational complexity depends on the chaotic initialization mechanism, DE mechanism, and original SSA. As mentioned earlier, N and MaxFEs signify group size and maximum fitness evolution number, respectively. Similarly, D means the dimension of the given problem, respectively. The computing time complexity of initialization process is O(N × D), The computing time complexity of chaotic initialization mechanism is O((N − 1) × N × D). Because the initial population and chaotic initialization consume N × N fitness evolutions. There are two fitness evolutions in each iteration, so the rest of the iterations are (MaxFEs − N × N)/2. In each iteration, the computing time complexity of updating the position by basic SSA is O(N × D), the computing time complexity of the DE mechanism is O(N × D), the computing time complexity of updating the global optimal solution is O(N). So, the computing time complexity of the proposed algorithm is O((N × D + (N − 1) × N × D) + (N × D + N × D + N) × (MaxFEs − N × N)/2), which can be simplified to O((2 × N × D + N) × ((MaxFEs − N × N)/2 + N × N × D)).
4 Experimental results
To estimate the performance of CDESSA, a series of experiments is conducted, firstly, the IEEE CEC2014 benchmark suite is used to test the performance of CDESSA in solving high-dimensional and multimodal problems; secondly, FS problems are adopted to evluate the capability of CDESSA in dealing with discrete optimization problems; finally, CDESSA is used to solve four constrained engineering optimization problems. All the experiments can evaluate the performance of CDESSA in handling global optimization problems comprehensively and objectively.
To be fair, as per standards in machine learning works [98,99,100,101] all the experiments were performed on the server with Intel (R) Xeon(R) E5-2650 v3 (2.30 GHz) CPU and 20 GB RAM, it runs Windows Server 2008 R2 version operating system, all the codes are implemented by MATLAB R2014b.
4.1 Experiment 1: results for IEEE CEC2014 problems
In this section, CDESSA is compared with the state-of-the-art algorithms on the IEEE CEC2014 benchmark suit. IEEE CEC2014 benchmark suite can be divided into four types such as unimodal, multimodal, hybrid, and composition functions. The summary of the CEC2014 benchmark suite is demonstrated in Table 1. In this experiment, to be fair, the swarm size N was 40, the maximum evaluations (MaxFEs) were set to D × 10,000, in which D is problem dimensions, at the same time each method runs 30 times on each function independently.
At the same time, seven competitive improved evolutionary algorithms are chosen to participate in this competition; the parameters of all the involved algorithms are listed in Table 2 in detail. The Wilcoxon singed-rank test [62] was utilized with a 0.05 significance level to measure whether there is a statistical significance between CDESSA and other competitors. In the results, “w’’ sign identifies that CDESSA is superior to the competitors, “t” symbol denotes a tie and so there is not a statistically significant difference, and “l” sign signifies CDESSA is inferior to the peer algorithms, and hence CDESSA exhibits the worse performance.
4.1.1 The impact of chaotic initialization and DE
As it was mentioned in Sect. 3, chaotic initialization and DE mechanism are integrated with the original SSA. To measure the influences of each strategy and acquire the best mechanism combinations for the next experiments. Among these combinations, CSSA indicates only a chaotic initialization mechanism is embedded in the original SSA; DESSA means only the DE mechanism is introduced in basic SSA; CDESSA denotes both chaotic initialization, and DE mechanism are applied to enhance the performance of SSA. All these mechanism combinations are evluated on the CEC2014 benchmark 30D test. Then, the Friedman test is employed to measure the differences between all strategies according to the average ranking value. The results of the Friedman test are displayed on Table 3. In Table 3, it can be observed that CDESSA gets the minimum average value of 1.8233 and the best rank No. 1. All these results indicate that the performance of CDESSA outperforms CSSA and DESAA. Based on the results, CDESSA with the best performance comparing with other mechanism combinations is chosen to take part in the following experiments as the proposed algorithm.
4.1.2 Diversity analysis and balance analysis
To measure the population diversity and the balance between exploration and exploitation of CDESSA and SSA in the search process, the diversity analysis and balance analysis experiment is conducted based on the IEEE CEC2014 benchmark 30D test, the population is formed by 40 agents, when iteration reachs 1000 the search process is terminated. The diversity and balance analysis convergence plots are indicated in Figs. 4 and 5, respectively.
In Fig. 4, the horizontal axis indicates the iteration number; the vertical axis denotes the average distance between the individuals in the population. It indicates the individual distribution in the current population. And then, it reveals the population diversity. In Fig. 4, at the initialization phase the mean distance between agents is much bigger because the agents are distrbuted randomly in the solution space, the curve will go down as the iteration increases, it will reach stabilization finally. At the initialization stage, the average distance between the agents of the CDESSA is much bigger than basic SSA owing to the chaotic initialization mechanism performed in the initialization. The chaotic initialization mechanism makes the initial population distributes more uniformly so that the population can search for more potential regions. It indicates that the proposed CDESSA has more diversity at the initial phase. The time at which the average distance between the agents in the CDESSA population reaches the steady-state is later than the original SSA. It can be ascribed to the DE mechanism, which enhances the exploration performance of SSA. It increases the diversity of the population and avoids the population being premature convergence to a certain extent.
In Fig. 5, the horizontal ordinate means the iteration number, the ordinate menas the percentage, the red curve denotes the exploration, the blue curve indicates the exploitation, an cyan incremental-decremental curve is appended in the chart, firstly, it increases from 0 to 100%, when the exploration and exploitation of the algorithm reach balance condition it reaches the biggest value 100%. After this moment, the exploitation curve rises to 100%, but the exploration curve falls to 0, the incremental-decremental curve also drops to 0, this phenomenon matches the optimization cycle of the population-based method, most of the population-based methods mainly performs the global searching stage to accelerate convergence rate in the base phase, in the later stage it carries out the exploitation step to boost the convergence accuracy. From Fig. 5, it can be found that the difference between the exploration and the exploitation in CDESSA is much higher than that in basic SSA, because that the chaotic initialization mechanism enhances the exploration at the initial stage. The moment that the exploration and exploitation of the algorithm archive balance are later in the CDESSA than that in the original SSA, this indicates that the DE mechanism boosts the exploration ability and makes it last longer, so the stable moment will be delayed. In the same way, the average exploration of CDESSA is bigger than the original SSA. This also demonstrates that the chaotic initialization mechanism and the DE mechanism promote the exploration performance of SSA.
4.1.3 Comparison with other state-of-the-art algorithms on 30D test
In this section, CDESSA is in comparison to other state-of-the-art methods at D = 30. The results of all the competitors for IEEE CEC2014 problems at D = 30 are shown in Appendix Table 19, which include mean and std values for each function. The overall ranking of all the methods based on the average value is listed in Table 4, the last row of Table 4 shows the total number that CDESSA wins, tie with, and loses to the corresponding competitor, respectively. The results of the Friedman test are exhibited in Table 5. The average execution time of each method on each function is demonstrated in Table 6. The convergence trend pictures of all the involved algorithms are demonstrated in Fig. 6.
Based on the results in Appendix Table 19 and the rangking table Table 4, it can be found that CDESSA outperforms ESSA and CSSA on all 30 functions; CDESSA wins ALCPSO on 21 functions, it loses to ALCPSO on 4 functions (F1, F2, F3, F10), it ties with ALCPSO on other 5 functions; CDESSA is superior to CLPSO on 18 functions, it is inferior to CLPSO on 8 functions (F2, F3, F4, F8, F10, F16, F18, F22); CDESSA outperforms DECLS on 23 functions, it is worse than DECLS on 6 functions (F2, F3, F7, F8, F10, F22), there is no statistically significant difference between CDESSA and DECLS on other one function; Compared with WDE, CDESSA gains more promising results on 17 functions, it loses to WDE on 11 functions (F1, F3, F4, F8, F10, F16, F17, F18, F20, F21, F22), it shows a tie on other 2 functions; Compared to CMSSA, CDESSA shows more competitive performance on 23 functions, it is behind CMSSA on 3 functions (F27, F29, F30), on other 4 functions CDESSA and CMSSA go to deuce. Based on the above analysis, it comes to a conclusion that on most of the Unimodal functions CDESSA does not demonstrate more competitive performance than ALCPSO, CLPSO, DECLS, and WDE, at the same time CDESSA does not acquire more promising results on Multimodal functions than WDE, but our proposed algorithm CDESSA shows more competitive performance on Hybrid, and Composition functions, these functions are more difficult to solve than Unimodal and Multimodal functions. In a word, our CDESSA gains the lowest rank value 2.4000 and ranks first, which means CDESSA can beat all the competitors on the IEEE CEC2014 benchmark suit.
The average ranking of all the peers obtained by the Friedman test is shown in Table 5, CDESSA gets the lowest average ranking 2.3622 and No. 1 rank, but the average ranking of No.2 rank CLPSO is 3.2356 who is more than CDESSA, which means CDESSA shows more disadvantage than other competitors.
The average execution time of all the compared algorithms on each function of IEEE CEC2014 problems at D = 30 is demonstrated in Table 6. From Table 6, it can be found that the time consumption of CMSSA is much bigger than other algorithms due to the chaotic exploitative mechanism (CEM), Gaussian and Cauchy mutation consume more computing time, CSSA and ESSA consume less computing time than other methods owing to it only modifies the parameters and does not introduce extra time consumption, the time consumption of the proposed CDESSA is similar to WDE, it costs less computing time than CMSSA. However, it spends more computing time than CSSA, ESSA, ALCPSO, CLPSO, DECLS. These results indicate that the time complexity of CDESSA is higher than CSSA, ESSA, ALCPSO, CLPSO, DECLS, it is lower than CMSSA; it is equal to WDE.
These results verify that the performance of CDESSA is improved significantly in comparison with the original SSA and other competitors. It also states clearly that the improvements between the CDESSA and other competitors are outstanding. The presented CDESSA performs better due to the following reasons. During the initialization, the chaotic initialization mechanism can obtain a better initial population through the less simulated stochastic process. It ensures that the initial population distributes as uniformly and randomly as possible, literature [52, 53] states clearly that a well-distributed initial population will promote the population to find a better optimal solution faster; during each iteration, the DE mechanism will enhance the exploitation and exploration of each salp as an intensification tool by mutation, crossover, and selection operators, more potential areas will be traversed. All the embedded mechanisms strengthen the exploitation and exploration capacity of the original SSA, so the proposed CDESSA has better convergence accuracy and faster convergence speed, as revealed in Fig. 6 the presented algorithm CDESSA can find a more promising solution quickly.
4.1.4 Scalability test for CDESSA
The scalability test for CDESSA was organized in this section. The dimensionality D is rose to 50 and 100 to estimate the capability of CDESSA in dealing with the benchmark problems with higher dimensions. These state-of-the-art algorithms were utilized as competitors as in Sect. 4.1.3. The comparison results of all the competitors on the IEEE CEC2014 benchmark set at D = 50 and 100 are exhibited in Appendix Tables 20 and 21, respectively. The overall ranking of all the methods based on the average value on the IEEE CEC2014 benchmark set at D = 50 and 100 are illustrated in Tables 7 and 8, respectively. From the last row in Tables 7 and 8, it can be seen that the victory function total number of the presented algorithm CDESSA is bigger than the lost function number and the tied function number compared with the competitors. It indicates that the proposed CDESSA outperforms all the peers. From the average Friedman ranking in Table 9, the presented CDESSA achieves the best average ranking value, which is 2.1433 and 1.9211 for D = 50 and 100, respectively. All the comparison results demonstrate that CDESSA holds distinct advantages in solving higher dimensions to optimize the problem. The CDESSA is far advance than the second one in dealing with higher dimensions problems.
Comparing the average Friedman ranking value for D = 50 and 100 with D = 30, it can be found that the average ranking value of the improved CDESSA drops from 2.3622 to 2.1433 and 1.9211 with the increasing dimensionality. It indicates that the enhanced CDESSA holds more advantages in higher dimensionality problems contrary to the competitors; it also means that the introduced mechanisms play a greater role in the high-dimensional problems.
4.2 Experiment 2: results for FS problems
In essence, FS is a kind of discrete optimization problem. This problem aims to choose as few features as possible and get rid of irrespective features to acquire the best classification precision. In this section, the presented CDESSA is adopted to deal with 12 diverse datasets from the UCI machine learning repository [66] comparing with four advanced FS algorithms such as BMFO, BSSA, BWOA, BFOA, SSAPSO [32]. The parameters of all the competitors are set as their original versions in the literature [6, 67,68,69], respectively. The details of the data sets are described in Table 10, including feature numbers and sample numbers of each dataset.
As we all know, in the beginning, CDESSA is designed for continuous real optimization problems, so it cannot be used to solve FS problems directly. It must be carried out binary transformation as follows.
In the initial stage, every dimension of each agent is assigned 0 or 1 randomly to acquire the binary value. This operation can be denoted as below.
where \(X_{i,j}\) indicates the jth dimension of the value of ith agent.
During the optimization process, each dimension of the continuous solution of each agent will be transformed into a binary value by the following transfer functions called the S-shaped transfer function,
where \(x\) indicates each dimension of the position of each agent, \({\text{posOut}}\) means the output binary value of the S-shaped transfer function. These functions realize the aim of transforming continuous real value to binary value.
During the process, each algorithm executes N (N means the population size of each method) times on each dataset and carries out K-fold crossover at each time. During each crossover, the data of each dataset will be divided into three sections: training set, validation set, and test set. First of all, the K nearest neighbor classifier (KNN) is applied to train and classify the data of the training set; then the training model will be verified on the validation set; finally, the selected features are performed on the test set with the objective of gaining the accuracy value.
In this work, whether each feature will be selected depends on the binary value of the corresponding dimension of the solution. If the value is 0, it indicates this feature is chosen; if the value is 1, it means this feature is abandoned. Each FS scheme that corresponds to the position of the agent is estimated based on the fitness acquired by the method. The fitness \(fit\) can be calculated by Eq. (15) as follows:
where \({\text{accuracy}}\) means the accuracy acquired by the algorithm on the validation set. \(N\) indicates the total feature number in the corresponding dataset. \(N_{i}\) is the feature number which is selected by the algorithm. The parameters \(\alpha\) and \(\beta\) are weight coefficients of the accuracy and feature number, respectively.
In this experiment, the maximum iteration is 50. The population size is 10. Each algorithm runs ten times randomly, Wilcoxon singed-rank test [62] was also utilized with a 0.05 significance level to measure whether there is a statistical significance between CDESSA and other competitors.
The comparison results of fitness obtained by competitors are shown in Appendix Table 22. From Appendix Table 22, it can be found that CDESSA acquires the best results on Breastcancer, primary-tumor, heart, M-of-n, SpectEW; at the same time, CDESSA obtains second best results on BreastEW, Exactly, Cleveland_heart, Tumors_14. The boxplot of fitness obtained by the competitors on datasets is demonstrated in Fig. 7 also supports this conclusion, and in Fig. 7, it can be seen that the fitness fluctuation range of CDESSA is smaller than the competitors on most datasets. The ranking values of peers illustrated in Table 11 indicate that our proposed algorithm CDESSA gets the best ranking value 2.5667 and first rank No.1. The results of the fitness state clearly that the presented CDESSA acquires the best FS set on the datasets. The convergence pictures of the compared algorithms on fitness are shown in Fig. 8. The convergence graphs indicate our proposed CDESSA holds a faster convergence speed against the competitors.
The comparison results of errors acquired by peers are demonstrated in Appendix Table 23. It can be found that CDESSA obtains the lowest error value on Exactly, primary-tumor, heart, SpectEW, CongressEW, Tumors_14; meanwhile, CDESSA obtains second best results on Breastcancer, M-of-n. The boxplot of error value obtained by the peers on datasets is illustrated in Fig. 9 also affirms this conclusion; at the same time, it can be found that the error volatility of CDESSA is lower than the compared algorithms on most of the datasets. The ranking values of all the compared algorithms shown in Table 12 make clear that our presented algorithm CDESSA obtains the best ranking value 2.5708 and first rank No.1. The results of the error value state clearly that the FS scheme found by CDESSA holds the highest accuracy rate on the classifier at the datasets.
The comparison results of the feature number gained by compared algorithms are illustrated in Appendix Table 24. From Appendix Table 24, it can be concluded that CDESSA obtains the smallest feature number on Exactly, primary-tumor, heart, CongressEW, Cleveland_heart; at the same time, CDESSA obtains second best results on BreastEW, M-of-n, CTG3. The boxplot of feature number acquired by the peers on datasets is demonstrated in Fig. 10 also indicates this, meanwhile, it can be discovered that CDESSA has a lower fluctuation on the feature number than rivals on most datasets in Fig. 10. The ranking values of competitors shown in Table 13 indicate that the proposed algorithm CDESSA obtains the best ranking value 2.7042 and No.1 rank value. The results of feature numbers indicate that CDESSA acquires the shortest FS set on the datasets. All the feature number results indicate that the FS set gained by CDESSA contains the fewest uncorrelated feature information.
4.3 Experiment 3: results for constrained engineering optimization problems
In this section, our proposed CDESSA is adopted to deal with five constrained engineering optimization problems. When solving these problems, for CDESSA the population size is set to 50. The maximum iteration is 2000, CDESSA runs 100 times randomly. The statistical results of all the compared algorithms are extracted from the corresponding references due to the best results reported by researchers.
4.3.1 Tension/compression spring design problem
Finding solutions using a developed approach needs a logical modeling process [70,71,72,73]. The spring design problem is a widespread case in the engineering design field. The objective of the spring design problem is to devise a minimum weight (\(f\left( x \right)\)) compression spring holding three variables: wire diameter (\(d\)), mean coil diameter (\(D\)), and the number of active coils (\(P\)) [74,75,76].
This problem holds the mathematical model as below:
consider \(x = \left[ {x_{1} ,x_{2} ,x_{3} } \right] = \left[ {d, D, P} \right]\).
object \(\min f\left( {\vec{x}} \right) = x_{1}^{2} x_{2} \left( {x_{3} + 2} \right)\).
subject to:
variable scope \(0.05 \le x_{1} \le 2.00, 0.25 \le x_{2} \le 1.30, 2.00 \le x_{3} \le 15.0\).
The best solution obtained by CDESSA for the tension/compression spring design problem is shown in Table 14. From Table 14, it can be found that CDESSA is superior to both original SSA and other competitors in solving tension/compression spring design problems. All the results indicate that CDESSA maintains a more competitive performance for tension/compression spring design problems, in which GA3 is the worst performer, ESSA performs the second best.
4.3.2 Welded beam design problem
Design a welded beam with minimum fabrication cost is another kind of typical engineering design problem. This problem holds four design variables, which are reported in detail in related refs [81].
To solve this problem, the corresponding mathematical model is built as below:
consider \(\vec{x} = \left[ {x_{1} ,x_{2} ,x_{3} , x_{4} } \right] = \left[ {h, l, t, b} \right]\)
object \(\min f\left( {\vec{x}} \right) = 1.10471x_{1}^{2} + 0.04811x_{3} x_{4} \left( {x_{4} + 14.0} \right)\)
subject to:
variable scope \(0.1 \le x_{1} , x_{4} \le 2.0, 0.1 \le x_{2} ,x_{3} \le 10.0\)
where \(\tau \left( {\vec{x}} \right) = \sqrt {\tau^{{\prime}{2}} + 2\tau^{\prime}\tau^{\prime\prime}\frac{{x_{2} }}{2R} + \tau^{{\prime\prime}{2}} } , \tau^{\prime} = \frac{P}{{\sqrt 2 x_{1} x_{2} }}, \tau^{\prime\prime} = \frac{MR}{J}\)
The best solution gained by CDESSA is shown in Table 15. From Table 17, it can be concluded that CDESSA further outperforms all the compared methods. The results got by other methods are all bigger than 1.72, but the proposed CDESSA is less than 1.7, the difference between CDESSA and other peers is obvious. It means the proposed CDESSA can find a more promising solution within the variable boundaries and restraints.
4.3.3 Pressure vessel design problem
This design problem aims to devise a pressure vessel using a minimum total cost under the constraints of material cost, forming cost, and welding cost. This problem contains four variables: the shell thickness (Ts), the head thickness (Th), inner radius (R), the cylindrical section length (L); in which, both Ts and Th are the integral multiples of 0.625 in [84].
The corresponding mathematical model of this problem is built as follows:
consider \(\vec{x} = \left[ {x_{1} ,x_{2} ,x_{3} , x_{4} } \right] = \left[ {T_{{\text{s}}} , T_{{\text{h}}} ,R, L} \right]\).
object \(\min f\left( {\vec{x}} \right) = 0.6224x_{1} x_{2} x_{3} x_{4} + 1.7781x_{3} x_{1}^{2} + 3.1661x_{4} x_{1}^{2} + 19.84x_{3} x_{1}^{2}\).
subject to:
variable scope \(0 \le x_{1} , x_{2} \le 100, 10 \le x_{3} ,x_{4} \le 200\).
The best solution gained by the proposed CDESSA is in Table 16. As shown in Table 16, it can be observed that the best result gained by CDESSA is much smaller than other peers, quality of the solution acquired by the competitors is more than 6000, our method CDESSA is only 5453.2428, the difference between CDESSA and other compared approaches is more than 600, so it means CDESSA is much better than other methods. All these results indicate that our method has a much more competitive performance in solving this problem.
4.3.4 Three-bar design problem
The goal of this problem is to design a truss using three bars with the minimum weight, it is a classical constraining optimization problem, it includes two variables: the cross-sectional areas of the bars (A1, A2) [89, 90].
To solve this problem its corresponding mathematical model can be constructed as follows:
consider \(x = \left[ {x_{1} ,x_{2} } \right] = \left[ {A_{1} , A_{2} } \right]\).
object \(\min f\left( {\vec{x}} \right) = \left( {2\sqrt {2x_{1} } + x_{2} } \right) \times l\).
subject to:
variable scope \(0 \le x_{1} \le 1, 0 \le x_{2} \le 1\). where \(l = 100\; {\text{cm}}\), \(P = 2\; {\text{KN}}/{\text{cm}}^{2}\), \(\sigma = 2\; {\text{KN}}/{\text{cm}}^{2}\).
The optimal results got by CDESSA and other competitors are demonstrated in Table 17. Based on the values in Table 17 it can be observed that DEDS, PSO-DE, SSA, and CDESSA obtain the same best result 263.8958434, Ray and Sain acquire the worst result 264.3. CDESSA shows better competitiveness in comparison to other evolutionary algorithms. So it can be used to solve the three-bar design problem effectively.
4.3.5 Multiple disk clutch brake design problem
This design problem is a kind of classical discrete optimization problem, its goal is to design a multiple disk clutch brake with both the minimum mass of the multiple disk clutch brake systems. This problem involves five variables: internal diameter (ri), external diameter (ro), the thickness of the disc (t), activating force (F), the number of frictional-force(Z). At the same time, the value range of ri and ro is [54, 73] and [83], respectively; their step size is both one. The variable t changes in the region [1], and its step size is 0.5. The value range of F is [600, 1000] and its step size is 10. The variable Z changes in the region, and its step size is one. It means the type of all the variables value is discrete [83, 95].
The corresponding mathematical model of this problem can be built as below:
consider \(\vec{x} = \left[ {x_{1} ,x_{2} ,x_{3} , x_{4} , x_{5} } \right] = \left[ {r_{i} , r_{o} ,t, F, Z} \right]\).
object \(\min f\left( {\vec{x}} \right) = \pi \left( {x_{2}^{2} - x_{1}^{2} } \right)x_{3} \left( {x_{5} + 1} \right)\rho\).
subject to:
where \(M_{{\text{h}}} = \frac{2}{3}\mu x_{4} x_{5} \frac{{x_{2}^{3} - x_{1}^{3} }}{{x_{2}^{2} - x_{1}^{2} }}{\text{N}}\;{\text{mm}}\), \(\omega = \frac{\pi n}{{30}}\; {\text{rad/s}}\), \(A = \pi \left( {x_{2}^{2} - x_{1}^{2} } \right) \;{\text{mm}}^{2}\), \(p_{rz} = \frac{{x_{a} }}{A}\; {\text{N/mm}}^{2} .\)
\(V_{{{\text{sh}}}} = \frac{{\pi R_{{{\text{sr}}}} n}}{30}\;{\text{mm/s}}\), \(R_{{{\text{sr}}}} = \frac{2}{3}\frac{{x_{2}^{3} - x_{1}^{3} }}{{x_{2}^{2} - x_{1}^{2} }} \;{\text{mm}}\), \(\Delta R = 20\; {\text{mm}}\), \(L_{\max } = 30 \;{\text{mm}}\), \(\mu = 0.5\)
\(p_{\max } = 1 {\text{MPa}}\), \(= 0.0000078\; {\text{kg/mm}}^{3}\), \(V_{{{\text{srmax}}}} = 10\; {\text{m/s}}\), \(s = 1.5\), \(T_{\max } = 15 {\text{s}}\).
\(n = 250 rpm\), \(M_{{\text{s}}} = 40 \;{\text{Nm}}\), \(M_{{\text{f}}} = 3 {\text{Nm}}\), \(I_{z} = 55 \;{\text{kg}}\;{\text{m}}^{2}\), \(\delta = 0.5 \;{\text{mm}}\), \(r_{{i,{\text{min}}}} = 60\; {\text{mm}}\).
\(r_{i,\max } = 80 {\text{mm}}\), \(r_{0,\min } = 90 {\text{mm}}\), \(r_{0,\max } = 110 {\text{mm}}\), \(t_{\min } = 1.5 {\text{mm}}\), \(t_{\max } = 3 {\text{mm}}\).
\(F_{\max } = 1000 {\text{N}}\), \(Z_{\max } = 9\).
This problem is a discrete combinatorial optimization problem, it needs to satisfy more constraints, so it is harder to solve. The best solutions acquired by CDESSA and other compared methods are shown in Table 18. It can be observed that CDESSA gets the best solution with the lowest function value 0.235242; CBA ranks second; WCA and TLBO acquire the same result 0.313656, PVS obtains the worst results 0.313660. It can be found that CDESSA is superior to other competitors and CDESSA holds more advantages.
5 Conclusions and future directions
In this study, the performance of SSA is enhanced by chaotic initialization and DE mechanism. The presented CDESSA was firstly estimated on IEEE CEC2014 benchmark problems to test the efficacy in solving high-dimensional and multimodal problems. Then, it is utilized to deal with feature selection problems and constrained engineering optimization problems. During the experiments, the proposed CDESSA is compared with the state-of-the-art algorithms. The results and evaluations verified the improved performance of CDESSA in terms of quality of results and convergence trends, and the Friedman test also shows that CDESSA is significantly superior to those competitors. The results verify that the chaotic initialization and DE mechanism enhance the exploration and exploitation capability of the original SSA effectively. The proposed mechanism in CDESSA can improve the equilibrium between the diversification and intensification cores of SSA and mitigate its convergence and stagnation shortcomings.
In future works, our research plans to focus on the following themes: firstly, introduce the surrogate model to CDESSA to reduce the computation cost; secondly, CDESSA will be applied to handle other challenging optimization problems, such as multi-objective problems, and dynamic optimization problems; then, chaotic initialization and DE strategy will be adopted to enhance the performance of other representative computational intelligence algorithms for engineering optimization problems, such as monarch butterfly optimization (MBO) [102], earthworm optimization algorithm (EWA) [103], elephant herding optimization (EHO) [104], moth search (MS) algorithm [105]; finally, the advanced adaptive DE [106, 107] and adaptive distributed DE [108–110] a lgorithms will be arranged to further enhance the performance of the proposed method.
References
Chen H, Zhang Q, Luo J, Xu Y, Zhang X (2019) An enhanced bacterial foraging optimization and its application for training kernel extreme learning machine. Appl Soft Comput. https://doi.org/10.1016/j.asoc.2019.105884
Heidari AA, Mirjalili S, Faris H, Aljarah I, Mafarja M, Chen H (2019) Harris hawks optimization: algorithm and applications. Futur Gener Comput Syst 97:849–872. https://doi.org/10.1016/j.future.2019.02.028
Yu H, Zhao N, Wang P, Chen H, Li C (2020) Chaos-enhanced synchronized bat optimizer. Appl Math Model 77:1201–1215. https://doi.org/10.1016/j.apm.2019.09.029
Li S, Chen H, Wang M, Heidari AA, Mirjalili S (2020) Slime mould algorithm: a new method for stochastic optimization. Futur Gener Comput Syst 111:300–323. https://doi.org/10.1016/j.future.2020.03.055
Wei Y, Lv H, Chen M, Wang M, Heidari AA, Chen H, Li C (2020) Predicting entrepreneurial intention of students: an extreme learning machine with gaussian barebone Harris Hawks optimizer. IEEE Access 8:76841–76855. https://doi.org/10.1109/ACCESS.2020.2982796
Mirjalili S, Gandomi AH, Mirjalili SZ, Saremi S, Faris H, Mirjalili SM (2017) Salp swarm algorithm: a bio-inspired optimizer for engineering design problems. Adv Eng Softw 114:163–191. https://doi.org/10.1016/j.advengsoft.2017.07.002
Zong WG, Joong HK, Loganathan GV (2001) A new heuristic optimization algorithm: harmony search. SIMULATION 76:60–68. https://doi.org/10.1177/003754970107600201
Kennedy J, Eberhart R (1995) Particle swarm optimization. In: Proceedings of ICNN'95—international conference on neural networks, vol 1944, pp 1942–1948. https://doi.org/10.1109/ICNN.1995.488968
Rashedi E, Nezamabadi-pour H, Saryazdi S (2009) GSA: a gravitational search algorithm. Inf Sci 179:2232–2248. https://doi.org/10.1016/j.ins.2009.03.004
Yang X-S (2012) Flower pollination algorithm for global optimization. In: Unconventional computation and natural computation, Berlin, pp 240–249. https://doi.org/10.1007/978-3-642-32894-7_27
Coello CAC, Pulido GT, Lechuga MS (2004) Handling multiple objectives with particle swarm optimization. IEEE Trans Evol Comput 8:256–279. https://doi.org/10.1109/TEVC.2004.826067
Zhang Q, Li H (2007) MOEA/D: a multiobjective evolutionary algorithm based on decomposition. IEEE Trans Evol Comput 11:712–731. https://doi.org/10.1109/TEVC.2007.892759
Abbassi A, Abbassi R, Heidari AA, Oliva D, Chen H, Habib A, Jemli M, Wang M (2020) Parameters identification of photovoltaic cell models using enhanced exploratory salp chains-based approach. Energy 198:117333. https://doi.org/10.1016/j.energy.2020.117333
Zhang Q, Chen H, Heidari AA, Zhao X, Xu Y, Wang P, Li Y, Li C (2019) Chaos-induced and mutation-driven schemes boosting salp chains-inspired optimizers. IEEE Access 7:31243–31261. https://doi.org/10.1109/access.2019.2902306
Gupta S, Deep K, Heidari AA, Moayedi H, Chen H (2021) Harmonized salp chain-built optimization. Eng Comput 37:1049–1079. https://doi.org/10.1007/s00366-019-00871-5
Faris H, Mirjalili S, Aljarah I, Mafarja M, Heidari AA (2020) Nature-inspired optimizers: theories, literature reviews and applications. Springer International Publishing, Cham, pp 185–199. https://doi.org/10.1007/978-3-030-12127-3_11
Faris H, Mafarja MM, Heidari AA, Aljarah I, Al-Zoubi AM, Mirjalili S, Fujita H (2018) An efficient binary salp swarm algorithm with crossover scheme for feature selection problems. Knowl Based Syst 154:43–67. https://doi.org/10.1016/j.knosys.2018.05.009
Sayed GI, Khoriba G, Haggag MH (2018) A novel chaotic salp swarm algorithm for global optimization and feature selection. Appl Intell 48:3462–3481. https://doi.org/10.1007/s10489-018-1158-6
Tubishat M, Ja’afar S, Alswaitti M, Mirjalili S, Idris N, Ismail MA, Omar MS (2021) Dynamic Salp swarm algorithm for feature selection. Expert Syst Appl 164:113873. https://doi.org/10.1016/j.eswa.2020.113873
El-Fergany AA (2018) Extracting optimal parameters of PEM fuel cells using salp swarm optimizer. Renew Energy 119:641–648. https://doi.org/10.1016/j.renene.2017.12.051
Zhang J, Wang Z, Luo X (2018) Parameter estimation for soil water retention curve using the salp swarm algorithm. Water 10(6):815. https://doi.org/10.3390/w10060815
Hussien AG, Hassanien AE, Houssein EH (2017) Swarming behaviour of salps algorithm for predicting chemical compound activities. In: 2017 eighth international conference on intelligent computing and information systems (ICICIS), pp 315–320. https://doi.org/10.1109/INTELCIS.2017.8260072
Zhao H, Huang G, Yan N (2018) Forecasting energy-related CO2 emissions employing a novel SSA-LSSVM model: considering structural factors in China. Energies. https://doi.org/10.3390/en11040781
Ateya AA, Muthanna A, Vybornova A, Algarni AD, Abuarqoub A, Koucheryavy Y, Koucheryavy A (2019) Chaotic salp swarm algorithm for SDN multi-controller networks. Eng Sci Technol 22:1001–1012. https://doi.org/10.1016/j.jestch.2018.12.015
Yang B, Zhong L, Zhang X, Shu H, Yu T, Li H, Jiang L, Sun L (2019) Novel bio-inspired memetic salp swarm algorithm and application to MPPT for PV systems considering partial shading condition. J Clean Prod 215:1203–1222. https://doi.org/10.1016/j.jclepro.2019.01.150
Wang J, Gao Y, Chen X (2018) A novel hybrid interval prediction approach based on modified lower upper bound estimation in combination with multi-objective salp swarm algorithm for short-term load forecasting. Energies 11:1–30. https://doi.org/10.3390/en11061561
Abbassi R, Abbassi A, Heidari AA, Mirjalili S (2019) An efficient salp swarm-inspired algorithm for parameters identification of photovoltaic cell models. Energy Convers Manag 179:362–372. https://doi.org/10.1016/j.enconman.2018.10.069
Abadi MQH, Rahmati S, Sharifi A, Ahmadi M (2021) HSSAGA: designation and scheduling of nurses for taking care of COVID-19 patients using novel method of hybrid salp swarm algorithm and genetic algorithm. Appl Soft Comput 108:107449. https://doi.org/10.1016/j.asoc.2021.107449
Abd el-sattar S, Kamel S, Ebeed M, Jurado F (2021) An improved version of salp swarm algorithm for solving optimal power flow problem. Soft Comput 25:4027–4052. https://doi.org/10.1007/s00500-020-05431-4
Ewees AA, Al-qaness MAA, Abd EM (2021) Enhanced salp swarm algorithm based on firefly algorithm for unrelated parallel machine scheduling with setup times. Appl Math Model 94:285–305. https://doi.org/10.1016/j.apm.2021.01.017
Salgotra R, Singh U, Singh S, Singh G, Mittal N (2021) Self-adaptive salp swarm algorithm for engineering optimization problems. Appl Math Model 89:188–207. https://doi.org/10.1016/j.apm.2020.08.014
Ibrahim RA, Ewees AA, Oliva D, Abd EM, Lu S (2019) Improved salp swarm algorithm based on particle swarm optimization for feature selection. J Ambient Intell Humaniz Comput 10:3155–3169. https://doi.org/10.1007/s12652-018-1031-9
Rizk-Allah RM, Hassanien AE, Elhoseny M, Gunasekaran M (2019) A new binary salp swarm algorithm: development and application for optimization tasks. Neural Comput Appl 31:1641–1663. https://doi.org/10.1007/s00521-018-3613-z
Bairathi D, Gopalani D (2021) An improved salp swarm algorithm for complex multi-modal problems. Soft Comput 25:10441–10465. https://doi.org/10.1007/s00500-021-05757-7
Braik M, Sheta A, Turabieh H, Alhiary H (2021) A novel lifetime scheme for enhancing the convergence performance of salp swarm algorithm. Soft Comput 25:181–206. https://doi.org/10.1007/s00500-020-05130-0
Nautiyal B, Prakash R, Vimal V, Liang G, Chen H (2021) Improved salp swarm algorithm with mutation schemes for solving global optimization and engineering problems. Eng Comput. https://doi.org/10.1007/s00366-020-01252-z
Ouaar F, Boudjemaa R (2021) Modified salp swarm algorithm for global optimisation. Neural Comput Appl 33:8709–8734. https://doi.org/10.1007/s00521-020-05621-z
Panda N, Majhi SK (2021) Oppositional salp swarm algorithm with mutation operator for global optimization and application in training higher order neural networks. Multimed Tools Appl. https://doi.org/10.1007/s11042-020-10304-x
Ren H, Li J, Chen H, Li C (2021) Stability of salp swarm algorithm with random replacement and double adaptive weighting. Appl Math Model 95:503–523. https://doi.org/10.1016/j.apm.2021.02.002
Saafan MM, El-Gendy EM (2021) IWOSSA: an improved whale optimization salp swarm algorithm for solving optimization problems. Expert Syst Appl 176:114901. https://doi.org/10.1016/j.eswa.2021.114901
Chen W, Zhang J, Lin Y, Chen N, Zhan Z, Chung HS, Li Y, Shi Y (2013) Particle swarm optimization with an aging leader and challengers. IEEE Trans Evol Comput 17:241–258. https://doi.org/10.1109/TEVC.2011.2173577
Liang JJ, Qin AK, Suganthan PN, Baskar S (2006) Comprehensive learning particle swarm optimizer for global optimization of multimodal functions. IEEE Trans Evol Comput 10:281–295. https://doi.org/10.1109/TEVC.2005.857610
Qin AK, Huang VL, Suganthan PN (2009) Differential evolution algorithm with strategy adaptation for global numerical optimization. IEEE Trans Evol Comput 13:398–417. https://doi.org/10.1109/TEVC.2008.927706
Brest J, Greiner S, Boskovic B, Mernik M, Zumer V (2006) Self-adapting control parameters in differential evolution: a comparative study on numerical benchmark problems. IEEE Trans Evol Comput 10:646–657. https://doi.org/10.1109/TEVC.2006.872133
Zhu A, Xu C, Li Z, Wu J, Liu Z (2015) Hybridizing grey wolf optimization with differential evolution for global optimization and test scheduling for 3D stacked SoC. J Syst Eng Electron 26:317–328. https://doi.org/10.1109/JSEE.2015.00037
Luo J, Chen H, Zhang Q, Xu Y, Huang H, Zhao X (2018) An improved grasshopper optimization algorithm with application to financial stress prediction. Appl Math Model 64:654–668. https://doi.org/10.1016/j.apm.2018.07.044
Çelik E, Öztürk N, Arya Y (2021) Advancement of the search process of salp swarm algorithm for global optimization problems. Expert Syst Appl 182:115292. https://doi.org/10.1016/j.eswa.2021.115292
Liu Y, Shi Y, Chen H, Heidari AA, Gui W, Wang M, Chen H, Li C (2021) Chaos-assisted multi-population salp swarm algorithms: framework and case studies. Expert Syst Appl 168:114369. https://doi.org/10.1016/j.eswa.2020.114369
Salgotra R, Singh U, Singh G, Singh S, Gandomi AH (2021) Application of mutation operators to salp swarm algorithm. Expert Syst Appl 169:114368. https://doi.org/10.1016/j.eswa.2020.114368
Zhang H, Wang Z, Chen W, Heidari AA, Wang M, Zhao X, Liang G, Chen H, Zhang X (2021) Ensemble mutation-driven salp swarm algorithm with restart mechanism: framework and fundamental analysis. Expert Syst Appl 165:113897. https://doi.org/10.1016/j.eswa.2020.113897
Andersen V, Nival P (1986) A model of the population dynamics of salps in coastal waters of the Ligurian Sea. J Plankton Res 8:1091–1110. https://doi.org/10.1093/plankt/8.6.1091
He Q, Wang L (2007) An effective co-evolutionary particle swarm optimization for constrained engineering design problems. Eng Appl Artif Intell 20:89–99. https://doi.org/10.1016/j.engappai.2006.03.003
Mahdavi M, Fesanghary M, Damangir E (2007) An improved harmony search algorithm for solving optimization problems. Appl Math Comput 188:1567–1579. https://doi.org/10.1016/j.amc.2006.11.033
Gao W-F, Huang L-L, Wang J, Liu S-Y, Qin C-D (2016) Enhanced artificial bee colony algorithm through differential evolution. Appl Soft Comput 48:137–150. https://doi.org/10.1016/j.asoc.2015.10.070
**ang W-L, Li Y-Z, Meng X-L, Zhang C-M, An M-Q (2017) A grey artificial bee colony algorithm. Appl Soft Comput 60:1–17. https://doi.org/10.1016/j.asoc.2017.06.015
Tian D, Zhao X, Shi Z (2019) Chaotic particle swarm optimization with sigmoid-based acceleration coefficients for numerical function optimization. Swarm Evol Comput 51:100573. https://doi.org/10.1016/j.swevo.2019.100573
Wang X, Wang Z, Weng J, Wen C, Chen H, Wang X (2018) A new effective machine learning framework for sepsis diagnosis. IEEE Access 6:48300–48310. https://doi.org/10.1109/ACCESS.2018.2867728
Zhang Q, Chen H, Luo J, Xu Y, Wu C, Li C (2018) Chaos enhanced bacterial foraging optimization for global optimization. IEEE Access 6:64905–64919. https://doi.org/10.1109/ACCESS.2018.2876996
Luo J, Chen H, Heidari AA, Xu Y, Zhang Q, Li C (2019) Multi-strategy boosted mutative whale-inspired optimization approaches. Appl Math Model 73:109–123. https://doi.org/10.1016/j.apm.2019.03.046
Tizhoosh HR (2005) Opposition-based learning: a new scheme for machine intelligence. In: international conference on computational intelligence for modelling, control and automation and international conference on intelligent agents, web technologies and internet commerce (CIMCA-IAWTIC'06), pp 695–701. https://doi.org/10.1109/CIMCA.2005.1631345
Chen H, Wang M, Zhao X (2020) A multi-strategy enhanced sine cosine algorithm for global optimization and constrained practical engineering problems. Appl Math Comput 369:124872. https://doi.org/10.1016/j.amc.2019.124872
Derrac J, García S, Molina D, Herrera F (2011) A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol Comput 1:3–18. https://doi.org/10.1016/j.swevo.2011.02.002
Jia D, Zheng G, Khurram KM (2011) An effective memetic differential evolution algorithm based on chaotic local search. Inf Sci 181:3175–3187. https://doi.org/10.1016/j.ins.2011.03.018
Civicioglu P, Besdok E, Gunen MA, Atasever UH (2020) Weighted differential evolution algorithm for numerical function optimization: a comparative study with cuckoo search, artificial bee colony, adaptive differential evolution, and backtracking search optimization algorithms. Neural Comput Appl 32:3923–3937. https://doi.org/10.1007/s00521-018-3822-5
Qais MH, Hasanien HM, Alghuwainem S (2019) Enhanced salp swarm algorithm: application to variable speed wind generators. Eng Appl Artif Intell 80:82–96. https://doi.org/10.1016/j.engappai.2019.01.011
Frank AA (2010) UCI machine learning repository
Pan W-T (2012) A new fruit fly optimization algorithm: taking the financial distress model as an example. Knowl Based Syst 26:69–74. https://doi.org/10.1016/j.knosys.2011.07.001
Mirjalili S (2015) Moth-flame optimization algorithm: a novel nature-inspired heuristic paradigm. Knowl Based Syst 89:228–249. https://doi.org/10.1016/j.knosys.2015.07.006
Mirjalili S, Lewis A (2016) The whale optimization algorithm. Adv Eng Softw 95:51–67. https://doi.org/10.1016/j.advengsoft.2016.01.008
Yang, S., Yu, X., Ding, M., He, L., Cao, G., Zhao, L.,... Ren, N. (2021). Simulating a combined lysis-cryptic and biological nitrogen removal system treating domestic wastewater at low C/N ratios using artificial neural network. Water research (Oxford), 189, 116576. doi: 10.1016/j.watres.2020.116576
Che, H., & Wang, J. (2021). A Two-Timescale Duplex Neurodynamic Approach to Mixed-Integer Optimization. IEEE transaction on neural networks and learning systems, 32(1), 36-48. doi: 10.1109/TNNLS.2020.2973760
Meng, Q., Lai, X., Yan, Z., Su, C., & Wu, M. (2021). Motion Planning and Adaptive Neural Tracking Control of an Uncertain Two-Link Rigid-Flexible Manipulator With Vibration Amplitude Constraint. IEEE transaction on neural networks and learning systems, PP, 1-15. doi: 10.1109/TNNLS.2021.3054611
Zhang, M., Chen, Y., & Susilo, W. (2020). PPO-CPQ: A Privacy-Preserving Optimization of Clinical Pathway Query for E-Healthcare Systems. IEEE internet of things journal, 7(10), 10660-10672. doi: 10.1109/JIOT.2020.3007518
Belegundu AD, Arora JS (1985) A study of mathematical programming methods for structural optimization. Part II: numerical results. Int J Numer Methods Eng 21:1601–1623. https://doi.org/10.1002/nme.1620210905
Coello Coello CA, Mezura Montes E (2002) Constraint-handling in genetic algorithms through the use of dominance-based tournament selection. Adv Eng Inform 16:193–203. https://doi.org/10.1016/S1474-0346(02)00011-3
Arora JS (2017) Introduction to optimum design, 4th edn. Academic Press, Boston, pp 601–680. https://doi.org/10.1016/B978-0-12-800806-5.00014-7
Krohling RA, Coelho L (2006) Coevolutionary particle swarm optimization using gaussian distribution for solving constrained optimization problems. IEEE Trans Syst Man Cybern Part B (Cybernetics) 36:1407–1416. https://doi.org/10.1109/TSMCB.2006.873185
Zahara E, Kao Y-T (2009) Hybrid Nelder–Mead simplex search and particle swarm optimization for constrained engineering design problems. Expert Syst Appl 36:3880–3886. https://doi.org/10.1016/j.eswa.2008.02.039
Li LJ, Huang ZB, Liu F, Wu QH (2007) A heuristic particle swarm optimizer for optimization of pin connected structures. Comput Struct 85:340–349. https://doi.org/10.1016/j.compstruc.2006.11.020
Zhang HL, Cai ZN, Ye XJ, Wang MJ, Kuang FJ, Chen HL, Li CY, Li YP (2020) A multi-strategy enhanced salp swarm algorithm for global optimization. Eng Comput. https://doi.org/10.1007/s00366-020-01099-4
Wang G-G, Guo L, Gandomi AH, Hao G-S, Wang H (2014) Chaotic Krill Herd algorithm. Inf Sci 274:17–34. https://doi.org/10.1016/j.ins.2014.02.123
Coello-Coello CA, Becerra RL (2004) Efficient evolutionary optimization through the use of a cultural algorithm. Eng Optim 36:219–236. https://doi.org/10.1080/03052150410001647966
Eskandar H, Sadollah A, Bahreininejad A, Hamdi M (2012) Water cycle algorithm—a novel metaheuristic optimization method for solving constrained engineering optimization problems. Comput Struct 110–111:151–166. https://doi.org/10.1016/j.compstruc.2012.07.010
Kannan BK, Kramer SN (1994) An augmented Lagrange multiplier based method for mixed integer discrete continuous optimization and its applications to mechanical design. J Mech Des 116:405–411. https://doi.org/10.1115/1.2919393
Sandgren E (1990) Nonlinear integer and discrete programming in mechanical design optimization. J Mech Des 112:223–229. https://doi.org/10.1115/1.2912596
Huang F-Z, Wang L, He Q (2007) An effective co-evolutionary differential evolution for constrained optimization. Appl Math Comput 186:340–356. https://doi.org/10.1016/j.amc.2006.07.105
He Q, Wang L (2007) A hybrid particle swarm optimization with a feasibility-based rule for constrained optimization. Appl Math Comput 186:1407–1422. https://doi.org/10.1016/j.amc.2006.07.134
Coelho L (2010) Gaussian quantum-behaved particle swarm optimization approaches for constrained engineering design problems. Expert Syst Appl 37:1676–1683. https://doi.org/10.1016/j.eswa.2009.06.044
Ray T, Liew KM (2003) Society and civilization: an optimization algorithm based on the simulation of social behavior. IEEE Trans Evol Comput 7:386–396. https://doi.org/10.1109/TEVC.2003.814902
Sadollah A, Bahreininejad A, Eskandar H, Hamdi M (2013) Mine blast algorithm: a new population based algorithm for solving constrained engineering optimization problems. Appl Soft Comput 13:2592–2612. https://doi.org/10.1016/j.asoc.2012.11.026
Ray T, Saini P (2001) Engineering design optimization using a swarm with an intelligent information sharing among individuals. Eng Optim 33:735–748. https://doi.org/10.1080/03052150108940941
Zhang M, Luo W, Wang X (2008) Differential evolution with dynamic stochastic selection for constrained optimization. Inf Sci 178:3043–3074. https://doi.org/10.1016/j.ins.2008.02.014
Liu H, Cai Z, Wang Y (2010) Hybridizing particle swarm optimization with differential evolution for constrained numerical and engineering optimization. Appl Soft Comput 10:629–640. https://doi.org/10.1016/j.asoc.2009.08.031
Gandomi AH, Yang X-S, Alavi AH (2013) Cuckoo search algorithm: a metaheuristic approach to solve structural optimization problems. Eng Comput 29:17–35. https://doi.org/10.1007/s00366-011-0241-y
Savsani P, Savsani V (2016) Passing vehicle search (PVS): a novel metaheuristic algorithm. Appl Math Model 40:3951–3978. https://doi.org/10.1016/j.apm.2015.10.040
Adarsh BR, Raghunathan T, Jayabarathi T, Yang X-S (2016) Economic dispatch using chaotic bat algorithm. Energy 96:666–675. https://doi.org/10.1016/j.energy.2015.12.096
Rao RV, Savsani VJ, Vakharia DP (2011) Teaching–learning-based optimization: a novel method for constrained mechanical design optimization problems. Comput Aided Des 43:303–315. https://doi.org/10.1016/j.cad.2010.12.015
Chen, S., Zhang, J., Meng, F., & Wang, D. (2021). A Markov Chain Position Prediction Model Based on Multidimensional Correction. Complexity (New York, N.Y.), 2021. https://doi.org/10.1155/2021/6677132
He, Y., Dai, L., & Zhang, H. (2020). Multi-Branch Deep Residual Learning for Clustering and Beamforming in User-Centric Network. IEEE communications letters, 24(10), 2221-2225. https://doi.org/10.1109/LCOMM.2020.3005947
Wu, X., Zheng, W., Chen, X., Zhao, Y., Yu, T., & Mu, D. (2021). Improving high-impact bug report prediction with combination of interactive machine learning and active learning. Information and Software Technology, 133, 106530.
Wu, Z., Cao, J., Wang, Y., Wang, Y., Zhang, L., & Wu, J. (2018). hPSD: a hybrid PU-learning-based spammer detection model for product reviews. IEEE transactions on cybernetics, 50(4), 1595-1606.
Wang, G. G., Deb, S., & Cui, Z. (2019). Monarch butterfly optimization. Neural computing and applications, 31(7), 1995-2014.
Wang, G. G., Deb, S., & Coelho, L. D. S. (2018). Earthworm optimisation algorithm: a bio-inspired metaheuristic algorithm for global optimisation problems. International journal of bio-inspired computation, 12(1), 1-22.
Wang, G. G., Deb, S., & Coelho, L. D. S. (2015, December). Elephant herding optimization. In 2015 3rd International Symposium on Computational and Business Intelligence (ISCBI) (pp. 1-5). IEEE. doi: 10.1109/ISCBI.2015.8
Wang, G. G. (2018). Moth search algorithm: a bio-inspired metaheuristic algorithm for global optimization problems. Memetic Computing, 10(2), 151-164.
Liu, X. F., Zhan, Z. H., Lin, Y., Chen, W. N., Gong, Y. J., Gu, T. L., ... & Zhang, J. (2018). Historical and heuristic-based adaptive differential evolution. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 49(12), 2623-2635.
Zhao, H., Zhan, Z. H., Lin, Y., Chen, X., Luo, X. N., Zhang, J., ... & Zhang, J. (2019). Local binary pattern-based adaptive differential evolution for multimodal optimization problems. IEEE transactions on cybernetics, 50(7), 3343-3357.
Zhan, Z. H., Wang, Z. J., **, H., & Zhang, J. (2019). Adaptive distributed differential evolution. IEEE transactions on cybernetics, 50(11), 4633-4647.
Zhan, Z. H., Liu, X. F., Zhang, H., Yu, Z., Weng, J., Li, Y., ... & Zhang, J. (2016). Cloudde: A heterogeneous differential evolution algorithm and its distributed cloud version. IEEE Transactions on Parallel and Distributed Systems, 28(3), 704-716.
Liu, X. F., Zhan, Z. H., & Zhang, J. (2021) Resource-Aware Distributed Differential Evolution for Training Expensive Neural-Network-Based Controller in Power Electronic Circuit. IEEE Transactions on Neural Networks and Learning Systems 1-11 10.1109/TNNLS.2021.3075205
Chen, Z. G., Zhan, Z. H., Wang, H., & Zhang, J. (2019). Distributed individuals for multiple peaks: A novel differential evolution for multimodal optimization problems. IEEE Transactions on Evolutionary Computation, 24(4), 708-719.
Chen, H., Li, S., Heidari, A. A., Wang, P., Li, J., Yang, Y., ... & Huang, C. (2020). Efficient multi-population outpost fruit fly-driven optimizers: Framework and advances in support vector machines. Expert Systems with Applications, 142, 112999.
Chen, H., Yang, C., Heidari, A. A., & Zhao, X. (2020). An efficient double adaptive random spare reinforced whale optimization algorithm. Expert Systems with Applications, 154, 113018.
Zhang, H., Heidari, A. A., Wang, M., Zhang, L., Chen, H., & Li, C. (2020). Orthogonal Nelder-Mead moth flame method for parameters identification of photovoltaic modules. Energy Conversion and Management, 211, 112764.
Ridha, H. M., Heidari, A. A., Wang, M., & Chen, H. (2020). Boosted mutation-based Harris hawks optimizer for parameters identification of single-diode solar cell models. Energy Conversion and Management, 209, 112660.
Chen, H., Jiao, S., Wang, M., Heidari, A. A., & Zhao, X. (2020). Parameters identification of photovoltaic cells and modules using diversification-enriched Harris hawks optimization with chaotic drifts. Journal of Cleaner Production, 244, 118778.
Chen, H., Heidari, A. A., Chen, H., Wang, M., Pan, Z., & Gandomi, A. H. (2020). Multi-population differential evolution-assisted Harris hawks optimization: Framework and case studies. Future Generation Computer Systems, 111, 175-198.
Acknowledgements
This work was supported in part by the college-enterprise cooperation project of the domestic visiting engineer of colleges (FG2020077), Zhejiang, China, General research project of Zhejiang Provincial Education Department (Y201942618), Zhejiang, China, the National Natural Science Foundation of China (62076185, U1809209), the Bei**g Natural Science Foundation (L182015), Zhejiang Provincial Natural Science Foundation of China (LY21F020030), Wenzhou Science & Technology Bureau (2018ZG016). We acknowledge comments of the reviewers.
Author information
Authors and Affiliations
Corresponding authors
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A
Appendix A
See Tables 19, 20, 21, 22, 23, and 24.
Rights and permissions
About this article
Cite this article
Zhang, H., Liu, T., Ye, X. et al. Differential evolution-assisted salp swarm algorithm with chaotic structure for real-world problems. Engineering with Computers 39, 1735–1769 (2023). https://doi.org/10.1007/s00366-021-01545-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00366-021-01545-x