SpringerLink
Log in

The Line-Tension Approximation as the Dilute Limit of Linear-Elastic Dislocations

  • Published:
Archive for Rational Mechanics and Analysis Aims and scope Submit manuscript

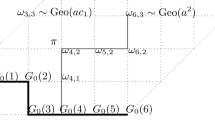
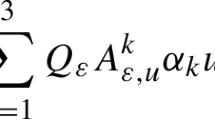Abstract

We prove that the classical line-tension approximation for dislocations in crystals, that is, the approximation that neglects interactions at a distance between dislocation segments and accords dislocations energy in proportion to their length, follows as the Γ-limit of regularized linear-elasticity as the lattice parameter becomes increasingly small or, equivalently, as the dislocation measure becomes increasingly dilute. We consider two regularizations of the theory of linear-elastic dislocations: a core-cutoff and a mollification of the dislocation measure. We show that both regularizations give the same energy in the limit, namely, an energy defined on matrix-valued divergence-free measures concentrated on lines. The corresponding self-energy per unit length \({\psi(b, t)}\), which depends on the local Burgers vector and orientation of the dislocation, does not, however, necessarily coincide with the self-energy per unit length \({\psi_0(b, t)}\) obtained from the classical theory of the prelogarithmic factor of linear-elastic straight dislocations. Indeed, microstructure can occur at small scales resulting in a further relaxation of the classical energy down to its \({\mathcal H^1}\)-elliptic envelope.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
EUR 32.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or Ebook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Brazil)

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Agmon S., Douglis A., Nirenberg L.: Estimates near the boundary for solutions of elliptic partial differential equations satisfying general boundary conditions. II. Commun. Pure Appl. Math. 17, 35–92 (1964)

    Article  MathSciNet  MATH  Google Scholar 

  2. Alberti G., Baldo S., Orlandi G.: Variational convergence for functionals of Ginzburg–Landau type. Indiana Univ. Math. J. 54(5), 1411–1472 (2005). doi:10.1512/iumj.2005.54.2601

    MathSciNet  MATH  Google Scholar 

  3. Alicandro R., Cicalese M., Ponsiglione M.: Variational equivalence between Ginzburg–Landau, XY spin systems and screw dislocations energies. Indiana Univ. Math. J. 60(1), 171–208 (2011). doi:10.1512/iumj.2011.60.4339

    Article  MathSciNet  MATH  Google Scholar 

  4. Alicandro R., De Luca L., Garroni A., Ponsiglione M.: Metastability and dynamics of discrete topological singularities in two dimensions: a Γ-convergence approach. Arch. Ration. Mech. Anal. 214(1), 269–330 (2014). doi:10.1007/s00205-014-0757-6

    Article  MathSciNet  MATH  Google Scholar 

  5. Ambrosio L., Braides A.: Functionals defined on partitions in sets of finite perimeter. I. Integral representation and Γ-convergence. J. Math. Pures Appl. (9) 69, 285–305 (1990)

    MathSciNet  MATH  Google Scholar 

  6. Ambrosio L., Braides A.: Functionals defined on partitions in sets of finite perimeter. II. Semicontinuity, relaxation and homogenization. J. Math. Pures Appl. (9) 69, 307–333 (1990)

    MathSciNet  MATH  Google Scholar 

  7. Ambrosio, L., Fusco, N., Pallara, D.: Functions of bounded variation and free discontinuity problems. In: Mathematical Monographs. Oxford University Press, Oxford, 2000

  8. Anzellotti G., Baldo S., Percivale D.: Dimension reduction in variational problems, asymptotic development in Γ-convergence and thin structures in elasticity. Asymptotic Anal. 9(1), 61–100 (1994)

    MathSciNet  MATH  Google Scholar 

  9. Ariza M.P., Ortiz M.: Discrete crystal plasticity. Arch. Ration. Mech. Anal. 178, 149–226 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  10. Bacon D.J., Barnett D.M., Scattergood R.O.: Anisotropic continuum theory of lattice defects. Progr. Mater. Sci. 23, 51–262 (1979)

    Article  ADS  Google Scholar 

  11. Barnett D., Swanger L.: The elastic energy of a straight dislocation in an infinite anisotropic elastic medium. Physica Status Solidi 48(b), 419–428 (1971)

    Article  ADS  Google Scholar 

  12. Bott, R., Tu, L.W.: Differential Forms in Algebraic Topology. Springer, Berlin, 1982

  13. Bourgain J., Brezis H.: New estimates for the Laplacian, the div-curl, and related Hodge systems. C. R. Math. Acad. Sci. Paris 338(7), 539–543 (2004). doi:10.1016/j.crma.2003.12.031

    Article  MathSciNet  MATH  Google Scholar 

  14. Bourgain J., Brezis H.: New estimates for elliptic equations and Hodge type systems. J. Eur. Math. Soc. (JEMS) 9(2), 277–315 (2007). doi:10.4171/JEMS/80

    Article  MathSciNet  MATH  Google Scholar 

  15. Bulatov, V., Cai, W.: Computer Simulations of Dislocations, Oxford Series on Materials Modelling, vol. 3. Oxford University Press, Oxford, 2013

  16. Cacace S., Garroni A.: A multi-phase transition model for the dislocations with interfacial microstructure. Interfaces Free Bound. 11, 291–316 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  17. Cermelli P., Leoni G.: Renormalized energy and forces on dislocations. SIAM J. Math. Anal. 37(4), 1131–1160 (2005). doi:10.1137/040621636

    Article  MathSciNet  MATH  Google Scholar 

  18. Conti, S., Garroni, A., Massaccesi, A.: Modeling of dislocations and relaxation of functionals on 1-currents with discrete multiplicity. Calc. Val. PDE (2014). doi:10.1007/s00526-015-0846-x

  19. Conti S., Garroni A., Müller S.: Singular kernels, multiscale decomposition of microstructure, and dislocation models. Arch. Rat. Mech. Anal. 199, 779–819 (2011). doi:10.1007/s00205-010-0333-7

    Article  MATH  Google Scholar 

  20. Conti, S., Gladbach, P.: A line-tension model of dislocation networks on several slip planes. Mech. Mat. (2015, to appear). doi:10.1016/j.mechmat.2015.01.013

  21. Dal Maso G., Murat F., Orsina L., Prignet A.: Renormalized solutions of elliptic equations with general measure data. Annali della Scuola Normale Superiore di Pisa, Classe di Scienze 4a serie 28(4), 741–808 (1999)

  22. De Luca L., Garroni A., Ponsiglione M.: Γ-convergence analysis of systems of edge dislocations: the self energy regime. Arch. Ration. Mech. Anal. 206(3), 885–910 (2012). doi:10.1007/s00205-012-0546-z

    Article  MathSciNet  MATH  Google Scholar 

  23. El Hajj A., Ibrahim H., Monneau R.: Dislocation dynamics: from microscopic models to macroscopic crystal plasticity. Contin. Mech. Thermodyn. 21(2), 109–123 (2009). doi:10.1007/s00161-009-0103-7

    Article  MathSciNet  ADS  MATH  Google Scholar 

  24. Federer, H.: Geometric measure theory. Die Grundlehren der mathematischen Wissenschaften, Band 153. Springer, New York, 1969

  25. Focardi M., Garroni A.: A 1D macroscopic phase field model for dislocations and a second order Γ-limit. Multiscale Model. Simul. 6(4), 1098–1124 (2007). doi:10.1137/070679181

    MathSciNet  Google Scholar 

  26. Friesecke G., James R.D., Müller S.: A theorem on geometric rigidity and the derivation of nonlinear plate theory from three-dimensional elasticity. Commun. Pure Appl. Math. 55(11), 1461–1506 (2002). doi:10.1002/cpa.10048

    Article  MATH  Google Scholar 

  27. Garroni A., Leoni G., Ponsiglione M.: Gradient theory for plasticity via homogenization of discrete dislocations. J. Eur. Math. Soc. (JEMS) 12(5), 1231–1266 (2010). doi:10.4171/JEMS/228

    Article  MathSciNet  MATH  Google Scholar 

  28. Garroni A., Müller S.: Γ-limit of a phase-field model of dislocations. SIAM J. Math. Anal. 36, 1943–1964 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  29. Garroni A., Müller S.: A variational model for dislocations in the line tension limit. Arch. Ration. Mech. Anal. 181, 535–578 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  30. Geers M.G.D., Peerlings R.H.J., Peletier M.A., Scardia L.: Asymptotic behaviour of a pile-up of infinite walls of edge dislocations. Arch. Ration. Mech. Anal. 209(2), 495–539 (2013). doi:10.1007/s00205-013-0635-7

    Article  MathSciNet  MATH  Google Scholar 

  31. Hall C.L., Chapman S.J., Ockendon J.R.: Asymptotic analysis of a system of algebraic equations arising in dislocation theory. SIAM J. Appl. Math. 70(7), 2729–2749 (2010). doi:10.1137/090778444

    Article  MathSciNet  MATH  Google Scholar 

  32. Hirsch, P.B.: Fifth International Conference on Crystallography, p. 139. Cambridge University, Cambridge, 1960

  33. Hirth, J.P., Lothe, J.: Theory of Dislocations. McGraw-Hill, New York, 1968

  34. Holz A.: Topological properties of linked disclinations in anisotropic liquids. J. Phys. A 24, L1259–L1267 (1991)

    Article  MathSciNet  ADS  Google Scholar 

  35. Holz A.: Topological properties of linked disclinations and dislocations in solid continua. J. Phys. A 25, L1–L10 (1992)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  36. Holz A.: Topological properties of static and dynamic defect configurations in ordered liquids. Physica A 182, 240–278 (1992)

    Article  MathSciNet  ADS  Google Scholar 

  37. Hull, D., Bacon, D.J.: Introduction to dislocations, 5th edn. Butterworth-Heinemann, Oxford, 2011

  38. Jerrard R.L.: Lower bounds for generalized Ginzburg–Landau functionals. SIAM J. Math. Anal. 30(4), 721–746 (1999). doi:10.1137/S0036141097300581

    Article  MathSciNet  MATH  Google Scholar 

  39. Kleman M., Michel L., Toulouse G.: Classification of topologically stable defects in ordered media. J. de Physique 38, L195–L197 (1977)

    Article  Google Scholar 

  40. Koslowski M., Cuitiño A.M., Ortiz M.: A phase-field theory of dislocation dynamics, strain hardening and hysteresis in ductile single crystal. J. Mech. Phys. Solids 50, 2597–2635 (2002)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  41. Koslowski M., Ortiz M.: A multi-phase field model of planar dislocation networks. Model. Simul. Mat. Sci. Eng. 12, 1087–1097 (2004)

    Article  ADS  Google Scholar 

  42. Kröner E.: Berechnung der elastischen Konstanten des Vielkristalls aus den Konstanten des Einkristalls. Zeitung der Physik 151, 504–518 (1958)

    Article  ADS  Google Scholar 

  43. Mermin N.D.: The topological theory of defects in ordered media. Rev. Modern Phys. 51(3), 591–648 (1979)

    Article  MathSciNet  ADS  Google Scholar 

  44. Morgan, F.: Geometric Measure Theory. Academic Press, Inc., Boston, 1988. A beginner’s guide

  45. Morrey, J.C.B.: Multiple Integrals in the Calculus Of Variations. Die Grundlehren der mathematischen Wissenschaften, Band 130. Springer, New York, 1966

  46. Müller S., Scardia L., Zeppieri C.I.: Geometric rigidity for incompatible fields and an application to strain-gradient plasticity. Indiana Univ. Math. J. 63, 1365–1396 (2014)

    Article  MathSciNet  Google Scholar 

  47. Mura, T.: Micromechanics of Defects in Solids. Kluwer Academic Publishers, Boston, 1987

  48. Nye J.F.: Some geometrical relations in dislocated crystals. Acta Metallurgica 1, 153–162 (1953)

    Article  Google Scholar 

  49. Orowan, E.: Discussion. Symposium on Internal Stresses in Metals and Alloys, p. 451. Institute of Metals, London, 1948

  50. Ponsiglione M.: Elastic energy stored in a crystal induced by screw dislocations: from discrete to continuous. SIAM J. Math. Anal. 39(2), 449–469 (2007). doi:10.1137/060657054

    Article  MathSciNet  MATH  Google Scholar 

  51. Read, W.T.J.: Dislocations in Crystals. McGraw-Hill, New York, 1953. p. 53

  52. Reina C., Conti S.: Kinematic description of crystal plasticity in the finite kinematic framework: a micromechanical understanding of F = F e F p. J. Mech. Phys. Solids 67, 40–61 (2014). doi:10.1016/j.jmps.2014.01.014

    Article  MathSciNet  ADS  Google Scholar 

  53. Rice, J.R.: Conserved integrals and energetic forces (Ed. Miller K.J. Fundamentals of Deformation and Fracture. Cambridge University Press, Cambridge, 1985

  54. Saada G.: Sur le durcissement dû à la recombinaison des dislocations. Acta Metallurgica 8, 841–847 (1960)

    Article  Google Scholar 

  55. Sandier E.: Lower bounds for the energy of unit vector fields and applications. J. Funct. Anal. 152(2), 379–403 (1998). doi:10.1006/jfan.1997.3170

    Article  MathSciNet  MATH  Google Scholar 

  56. Sandier, E., Serfaty, S.: Vortices in the Magnetic Ginzburg–Landau Model. Progress in Nonlinear Differential Equations and their Applications, Vol. 70. Birkhäuser, Boston, 2007

  57. Scala, R., Goethem, N.V.: Dislocations at the continuum scale: functional setting and variational properties (2013, Preprint)

  58. Scardia L., Zeppieri C.: Line-tension model for plasticity as the Γ-limit of a nonlinear dislocation energy. SIAM J. Math. Anal. 44, 2372–2400 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  59. Simpson H.C., Spector S.J.: On the positivity of the second variation in finite elasticity. Arch. Rat. Mech. Anal. 98(1), 1–30 (1987). doi:10.1007/BF00279960

    Article  MathSciNet  MATH  Google Scholar 

  60. Simpson H.C., Spector S.J.: Applications of estimates near the boundary to regularity of solutions in linearized elasticity. SIAM J. Math. Anal. 41(3), 923–935 (2009). doi:10.1137/080722990

    Article  MathSciNet  MATH  Google Scholar 

  61. Stampacchia G.: Le probléme de Dirichlet pour les équations elliptiques du second ordre à coefficients discontinus. Annales du Institut Fourier (Grenoble) 15, 189–258 (1965)

    Article  MathSciNet  MATH  Google Scholar 

  62. Stein, E.M.: Singular Integrals and Differentiability Properties of Functions. Princeton Mathematical Series, No. 30. Princeton University Press, Princeton, 1970

  63. Taylor G.I.: Mechanism of plastic deformation of crystals. Proc. R. Soc. London A 145, 362 (1934)

    Article  ADS  MATH  Google Scholar 

  64. Toulouse G., Kleman M.: Principles of a classification of defects in ordered media. J. Physique 37, L149–L151 (1976)

    Article  Google Scholar 

  65. Trebin H.R.: The topology of non-uniform media in condensed matter physics. Adv. Phys. 31(3), 195–254 (1982)

    Article  MathSciNet  ADS  Google Scholar 

  66. Van Schaftingen J.: Estimates for L 1-vector fields. C. R. Math. Acad. Sci. Paris 339(3), 181–186 (2004). doi:10.1016/j.crma.2004.05.013

    Article  MathSciNet  MATH  Google Scholar 

  67. Vitek V.: Theory of the core structures of dislocations in body-centred-cubic metals. Crystal Lattice Defects 5, 1–34 (1974)

    Google Scholar 

  68. de Wit G., Köhler J.S.: Interaction of dislocations with an applied stress in anisotropic crystals. Phys. Rev. 116(5), 1113–1120 (1959)

    Article  Google Scholar 

  69. Xu W., Moriarty J.A.: Atomistic simulation of ideal shear strength, point defects, and screw dislocations in bcc transition metals: Mo as a prototype. Phys. Rev. B 54(10), 6941–6951 (1996)

    Article  ADS  Google Scholar 

  70. Yang L.H., Soderlind P., Moriarty J.A.: Accurate atomistic simulation of \({(a/2)\langle111\rangle}\) screw dislocations and other defects in bcc tantalum. Philos. Mag. A 1(5), 1355–1385 (2001)

    Article  Google Scholar 

  71. Zehebauer M., Seumer V.: Cold work hardening in stages iv and v of fcc metals—i. experiments and interpretation. Acta Metallurgica et Materialia 45(2), 577–588 (1993)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institut für Angewandte Mathematik, Universität Bonn, 53115, Bonn, Germany

    Sergio Conti

  2. Dipartimento di Matematica, Università di Roma, Sapienza, 00185, Rome, Italy

    Adriana Garroni

  3. Division of Engineering and Applied Science, California Institute of Technology, Pasadena, CA, 91125, USA

    Michael Ortiz

Authors
  1. Sergio Conti
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Adriana Garroni
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Michael Ortiz
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Michael Ortiz.

Additional information

Communicated by The Editors

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Conti, S., Garroni, A. & Ortiz, M. The Line-Tension Approximation as the Dilute Limit of Linear-Elastic Dislocations. Arch Rational Mech Anal 218, 699–755 (2015). https://doi.org/10.1007/s00205-015-0869-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00205-015-0869-7

Keywords

Search

Navigation