SpringerLink
Log in

Application of shuffled frog-lea** algorithm on clustering

  • ORIGINAL ARTICLE
  • Published:
The International Journal of Advanced Manufacturing Technology Aims and scope Submit manuscript

Abstract

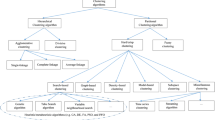
Evolutionary algorithms, such as shuffled frog lea**, are stochastic search methods that mimic natural biological evolution and/or the social behavior of species. Such algorithms have been developed to arrive at near-optimum solutions to complex and large-scale optimization problems which cannot be solved by gradient-based mathematical programming techniques. The shuffled frog-lea** algorithm draws its formulation from two other search techniques: the local search of the “particle swarm optimization” technique and the competitiveness mixing of information of the “shuffled complex evolution” technique. Cluster analysis is one of the attractive data mining techniques which is used in many fields. One popular class of data clustering algorithms is the center-based clustering algorithm. K-means is used as a popular clustering method due to its simplicity and high speed in clustering large datasets. However, k-means has two shortcomings: Dependency on the initial state and convergence to local optima and global solutions of large problems cannot be found with reasonable amount of computation effort. In order to overcome local optima problem, lots of studies are done in clustering. In this paper, we proposed an application of shuffled frog-lea** algorithm in clustering (SFLK-means). We compared SFLK-means with other heuristics algorithm in clustering, such as GAK, SA, TS, and ACO, by implementing them on several simulations and real datasets. Our finding shows that the proposed algorithm works better than others.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Ward JW (1963) Hierarchichal grou** to optimize an objective function. J Am Stat Assoc 58:236–244. doi:10.2307/2282967

    Article  Google Scholar 

  2. Selim SZ, Ismail MA (1984) K-means type algorithms: a generalized convergence theorem and characterization of local optimality. IEEE Trans Pattern Anal Mach Intell 6:81–87

    Article  MATH  Google Scholar 

  3. Spath H (1989) Clustering analysis algorithms. Ellis Horwood, Chichester, UK

    Google Scholar 

  4. Maulik U, Bandyopadhyay S (2000) Genetic algorithm-based clustering technique. Pattern Recognition 33:1455–1465

    Article  Google Scholar 

  5. Krishna K, Murty N (1999) Genetic k-means algorithm. IEEE Trans Syst, Man Cybernet—Part B: Cybernetics 29:433–439

    Article  Google Scholar 

  6. Shokri Z, Selim, Al-Sultan K (1991) A simulated annealing algorithm for the clustering problem. Pattern Recognition 24(10):1003–1008. doi:10.1016/0031-3203(91)90097-O

    Article  MathSciNet  Google Scholar 

  7. Sung CS, ** HW (2000) A Tabu-search-based heuristic for clustering. Pattern Recognition 33:849–858. doi:10.1016/S0031-3203(99)00090-4

    Article  Google Scholar 

  8. Kuo RI, Wang HS, Hu T-L, Chou SH (2005) Application of ant K-means on clustering analysis. Comput Math Appl 50:1709–1724. doi:10.1016/j.camwa.2005.05.009

    Article  MATH  MathSciNet  Google Scholar 

  9. Shelokar PS, Jayaraman VK, Kulkarni BD (2004) An ant colony approach for clustering. Anal Chim Acta 509:187–195. doi:10.1016/j.aca.2003.12.032

    Article  Google Scholar 

  10. Garey MR, Johnson DS, Witsenhausen HS (1982) The complexity of the generalized Lloyd–Max problem. IEEE Trans Inf Theory 28(2):255–256. doi:10.1109/TIT.1982.1056488

    Article  MATH  MathSciNet  Google Scholar 

  11. Gungor Z, Unler A (2007) K-harmonic means data clustering with simulated annealing heuristic. Appl Math Comput 184:199–209

    Article  MathSciNet  Google Scholar 

  12. Reynolds CW (1987) Flocks, herds and schools: a distributed behavioral model. Comput Graph 21(4):25–34. doi:10.1145/37402.37406

    Article  MathSciNet  Google Scholar 

  13. Heppner F, Grenander U (1990) A stochastic nonlinear model for coordinated bird flocks. In: Krasner S (ed) The ubiquity of chaos. AAAS, Washington, DC, pp 233–238

    Google Scholar 

  14. Wilson EO (1975) Sociobiology: the new synthesis. Belknap, Cambridge, MA

    Google Scholar 

  15. Eusuff M, Lansey K, Pasha F (2006) Shuffled frog-lea** algorithm: a memetic meta-heuristic for discrete optimization. Eng Optim 38(2):129–154. doi:10.1080/03052150500384759

    Article  MathSciNet  Google Scholar 

  16. Kennedy J, Eberhart R (1995) Particle swarm optimization. Proceedings of the IEEE International Conference on Neural Networks. IEEE Service Center, Piscataway, NJ, pp 1942–1948

  17. Duan QY, Gupta VK, Sorooshian S (1993) Shuffled complex evolution approach for effective and efficient global minimization. J Optim Theory Appl 76:502–521. doi:10.1007/BF00939380

    Article  MathSciNet  Google Scholar 

  18. Eusuff MM, Lansey KE (2003) Optimizing of water distribution network design using the shuffled frog lea** algorithm. J Water Resour Plan Manage 129(3):210–225. doi:10.1061/(ASCE)0733-9496(2003)129:3(210)

    Article  Google Scholar 

  19. Elbeltagi E, Hegazy T, Grierson D (2005) Comparison among five evolutionary-based optimization algorithms. J Adv Eng Inform 19:43–53. doi:10.1016/j.aei.2005.01.004

    Article  Google Scholar 

  20. Pal SK, Majumder DD (1977) Fuzzy sets and decision making approaches in vowel and speaker recognition.. IEEE Trans Syst Man Cybernet SMC-7:625–629

    Google Scholar 

  21. Blake CL, Merz CJ. UCI repository of machine learning databases. Available from <http://www.ics.uci.edu/_mlearn/MLRepository.html>

  22. Johnson RA, Wichern DW (1982) Applied multivariate statistical analysis. Prentice-Hall, Englewood Cliffs, NJ

    MATH  Google Scholar 

  23. Emad E, Tarek H, Donald G (2005) Comparison among five evolutionary-based optimization algorithms. Adv Eng Inform 19:43–53. doi:10.1016/j.aei.2005.01.004

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Industrial Engineering, Iran University of Science and Technology, Tehran, Iran

    Babak Amiri

  2. Department of Industrial Engineering, Iran University of Science and Technology, Tehran, Iran

    Mohammad Fathian

  3. Department of Electrical and Electronic Engineering, Iran University of Science and Technology, Tehran, Iran

    Ali Maroosi

Authors
  1. Babak Amiri
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Mohammad Fathian
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Ali Maroosi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Babak Amiri.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Amiri, B., Fathian, M. & Maroosi, A. Application of shuffled frog-lea** algorithm on clustering. Int J Adv Manuf Technol 45, 199–209 (2009). https://doi.org/10.1007/s00170-009-1958-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00170-009-1958-2

Keywords

Search

Navigation