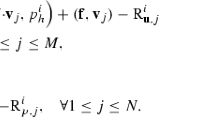SpringerLink
Log in

A posteriori error estimators for the Stokes equations II non-conforming discretizations

  • Published:
Numerische Mathematik Aims and scope Submit manuscript

Summary

We present an a posteriori error estimator for the non-conforming Crouzeix-Raviart discretization of the Stokes equations which is based on the local evaluation of residuals with respect to the strong form of the differential equation. The error estimator yields global upper and local lower bounds for the error of the finite element solution. It can easily be generalized to the stationary, incompressible Navier-Stokes equations and to other non-conforming finite element methods. Numerical examples show the efficiency of the proposed error estimator.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
EUR 32.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or Ebook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Germany)

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Adams, R.A. (1975): Sobolev Spaces. Academic Press, New York

    Google Scholar 

  2. Babuska, I., Rheinboldt, W.C. (1978): A posteriori error estimates for the finite element method. Int. J. Numer. Methods in Engrg.12, 1597–1615

    Google Scholar 

  3. Babuska, I., Rheinboldt, W.C. (1976): Error estimates for adaptive finite element computations. SIAM J. Numer. Anal.15, 736–754

    Google Scholar 

  4. Bank, R.E., Weiser, A. (1985): Some a posteriori error estimators for elliptic partial differential equations. Math. Comput.44, 283–301

    Google Scholar 

  5. Bank, R.E., Welfert, B.D. (1990): A posteriori error estimates for the Stokes equations: a comparison. Comp. Meth. Appl. Mech. Engrg.82, 323–340

    Google Scholar 

  6. Bank, R.E., Welfert, B.D. (1990): A posteriori error estimates for the Stokes problem. Preprint, Univ. of California San Diego

  7. Bernardi, C., Raugel, G. (1981): Méthodes d'éléments finis mixtes pour les équations de Stokes et de Navier-Stokes dans un polygone non-convexe. Calcolo18, 255–291

    Google Scholar 

  8. Braess, D., Verfürth, R. (1990): Multi-grid methods for non-conforming finite element methods. SIAM J. Numer. Anal.27, 979–986

    Google Scholar 

  9. Brenner, S. (1988): Multigrid methods for nonconforming finite elements. PhD Thesis, Univ. of Michigan

  10. Brenner, S. (1990): A nonconforming multigrid method for the stationary Stokes equations. Math. Comput.55, 411–437

    Google Scholar 

  11. Brezzi, F., Rappaz, J., Raviart, P.A. (1980): Finite dimensional approximation of non-linear problems I. Branches of non-singular solutions. Numer. Math.36, 1–25 (1980)

    Google Scholar 

  12. Clément, P. (1975): Approximation by finite element functions using local regularization. RAIRO Anal. Numér.9, 77–84

    Google Scholar 

  13. Crouzeix, M., Raviart, P.A. (1973): Conforming and non-conforming finite element methods for solving the stationary Stokes equations. RAIRO Anal. Numér.7, 33–76

    Google Scholar 

  14. Dobrowolski, M., Thomas, K. (1984): On the use of discrete solenoidal finite elements for approximating the Navier-Stokes equation. In: Application of Mathematics in Technology, Proc. Ger.-Ital. Symp., Rome pp. 246–262

  15. Dörfler, W. (1990): The condition of the stiffness matrix for certain elements approximating the incompressibility condition in fluid dynamics. Numer. Math.58, 203–214

    Google Scholar 

  16. Eriksson, K., Johnson, C. (1988): An adaptive finite element method for linear elliptic problems. Math. Comput.50, 361–383

    Google Scholar 

  17. Girault, V., Raviart, P.A. (1986): Finite element approximation of the Navier-Stokes equations. Computational Methods in Physics. Springer, Berlin Heidelberg New York

    Google Scholar 

  18. Griffiths, D.F. (1979): Finite elements for incompressible flow. Math. Meth. Appl. Sci.1, 16–31

    Google Scholar 

  19. Kellogg, R.B., Osborn, J.E. (1976): A regularity result for the Stokes problem in a convex polygon. J. Funct. Anal.21, 397–431

    Google Scholar 

  20. Verfürth, R. (1989): A posteriori error estimators for the Stokes equations. Numer. Math.55, 309–325

    Google Scholar 

  21. Verfürth, R. (1990): A posteriori error estimators and adaptive mesh-refinement for a mixed finite element discretization of the Navier-Stokes equations. In: W. Hackbusch, R. Rannacher, eds., Proc. 5th GAMM Conf. on Numerical Methods for the Navier-Stokes Equations. Vieweg, Braunschweig, pp. 145–152

    Google Scholar 

  22. Verfürth, R. (1989): On the preconditioning of non-conforming solenoidal finite element approximations of the Stokes equation. Preprint, Universität Zürich

  23. Verfürth, R. (1989): FEMFLOW-user guide. Version 1. Preprint, Universität Zürich

  24. Welfert, B.D. (1990): A posteriori error estimates for the Stokes problem. PhD Thesis, Univ. of California San Diego

Download references

Author information

Authors and Affiliations

  1. Institut für Angewandte Mathematik, Universität Zürich, Rämistrasse 74, CH-8001, Zürich, Switzerland

    R. Verfürth

Authors
  1. R. Verfürth
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Verfürth, R. A posteriori error estimators for the Stokes equations II non-conforming discretizations. Numer. Math. 60, 235–249 (1991). https://doi.org/10.1007/BF01385723

Download citation

  • Received:

  • Revised:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF01385723

Mathematics Subject Classification (1991)

Search

Navigation