Highly Efficient $GF(2^8)$ Inversion Circuit Based on Redundant GF Arithmetic and Its Application to AES Design

Abstract

This paper proposes a compact and efficient $GF(2^8)$ inversion circuit design based on a combination of non-redundant and redundant Galois Field (GF) arithmetic. The proposed design utilizes redundant GF representations, called Polynomial Ring Representation (PRR) and Redundantly Represented Basis (RRB), to implement $GF(2^8)$ inversion using a tower field $GF((2^4)^2)$. In addition to the redundant representations, we introduce a specific normal basis that makes it possible to map the former components for the 16th and 17th powers of input onto logic gates in an efficient manner. The latter components for $GF(2^4)$ inversion and $GF(2^4)$ multiplication are then implemented by PRR and RRB, respectively. The flexibility of the redundant representations provides efficient map**s from/to the $GF(2^8)$. This paper also evaluates the efficacy of the proposed circuit by means of gate counts and logic synthesis with a 65 nm CMOS standard cell library and comparisons with conventional circuits, including those with tower fields $GF(((2^2)^2)^2)$. Consequently, we show that the proposed circuit achieves approximately 40 % higher efficiency in terms of area-time product than the conventional best $GF(((2^2)^2)^2)$ circuit excluding isomorphic map**s. We also demonstrate that the proposed circuit achieves the best efficiency (i.e., area-time product) for an AES encryption S-Box circuit including isomorphic map**s.

1 Introduction

The substitution function, sometimes defined as arithmetic functions over $GF(2^m)$, is one of the most important parts of the Substitution Permutation Network (SPN) and Feistel structures [6]. Inversion functions, in particular, play an essential role in modern ciphers. Many ISO/IEC standard ciphers, such as AES and Camellia, employ an inversion function over $GF(2^8)$ in substitution functions [1, 9]. For example, SubBytes of AES consists of an inversion over $GF(2^8)$ (i.e., S-Box) and an affine transformation over GF(2). The hardware performance of such ciphers heavily depends on the inversion circuits used. As a result of the explosive increase in resource-constrained devices in the context of Internet of Things (IoT) applications, there is currently substantial demand for lightweight implementation of inversion functions.

Many approaches to reducing the hardware cost of $GF(2^8)$ inversion circuits have been proposed. Among them, the tower field approach, which calculates $a^{-1}$ $(= a^{254})$ $(a \in GF(2^8))$ using the equivalent tower field, is a promising approach for achieving the compact implementation. This technique converts the original field $GF(2^8)$ into a tower field, such as $GF(((2^2)^2)^2)$ and $GF((2^4)^2)$, in the middle of the inversion. Researchers have previously shown that the tower field approach is efficient because the subfields $GF((2^2)^2)$ and $GF(2^4)$ operations are designed more compactly than the original field operations. Satoh and Morioka [14] were the first to present a compact implementation of the AES S-Box by the tower field $GF(((2^2)^2)^2)$ represented by Polynomial Bases (PB). Canright [3] further reduced the gate count of the AES S-Box by using Normal Bases (NB) and optimizing the isomorphic map**s. Canright’s implementation was the smallest for a long time. Nogami et al. [11] recently mixed polynomial and normal bases to achieve the most efficient implementation. They showed that the product of gate count and critical delay for the inversion circuit could be reduced by the Mixed Bases (MB). Some implementations using $GF((2^4)^2)$ have also been proposed by researchers such as Rudra et al. [13] and Jeon et al. [8], who presented PB-based $GF((2^4)^2)$ inversion circuit designs. These results suggest that such field representations have a significant impact on hardware performance.

The above bases (i.e., PB, NB, and MB) represent each element of $GF(2^m)$ using m bits in a non-redundant manner. However, there are two redundant representations, namely, Polynomial Ring Representation (PRR) and Redundantly Represented Basis (RRB), which use n $(> m)$ bits to represent each element of $GF(2^m)$. The modular polynomial of these redundant representations is given by an n-degree reducible polynomial, whereas that of non-redundant representations is given by an m-degree irreducible polynomial. This means that redundant representations provide a wider variety of polynomials that can be selected as a modular polynomial than non-redundant representations. Drolet [5] showed that the use of PRR makes it possible to select a binomial $x^n+1$ as a modular polynomial, which can lead to the design of small-complexity arithmetic circuits. Wu et al. [16] and Nekado et al. [10] showed that RRB-based designs were useful for designing efficient inversion circuits.

This paper presents a technique in which non-redundant and redundant GF arithmetic are combined to achieve a compact and efficient $GF(2^8)$ inversion circuit design. The key idea underlying the proposed circuit is calculation of the inversion of the tower field $GF((2^4)^2)$ by the NB, PRR, and RRB combination. The former part for the 16th and 17th powers of the input is calculated by an NB with a symmetric property. This is followed by calculation of the latter parts for $GF(2^4)$ inversion and $GF(2^4)$ multiplication by PRR and RRB, respectively. The map** from NB to PRR/RRB is efficiently implemented by the symmetric property of the NB. The efficacy of the proposed circuit is evaluated by means of gate counts and logic synthesis results using a TSMC 65 nm CMOS standard cell library. The proposed circuit is approximately 19 % higher efficiency (i.e., area-time product) excluding isomorphic map**s than any other conventional circuits, including those with the tower field $GF(((2^2)^2)^2)$. In addition, the flexibility of redundant representations in the proposed circuit enables it to have the best efficiency even including isomorphic map**s from/to $GF(2^8)$. To the best of our knowledge, the proposed circuit is the most efficient tower field arithmetic-based implementation for the AES encryption S-Box.

The remainder of this paper is organized as follows. Section 2 introduces preliminary and related work associated with the design of $GF(2^8)$ inversion circuits. The redundant GF representations introduced in the proposed circuit are also described. Section 3 presents the proposed $GF(2^8)$ inversion circuit. Section 4 evaluates the proposed circuit by comparing the results of gate count and logic synthesis with those from conventional circuits. Section 5 presents the AES S-Box design that incorporates the proposed inversion circuit and its isomorphic map**s. Finally, Sect. 6 presents concluding remarks.

2 Preliminaries and Related Works

2.1 Inversion Circuits by Tower Fields

This section briefly describes previous work on the design of $GF(2^8)$ inversion circuits based on tower field arithmetic. The inverse element of a non zero $a \in GF(2^8)$ is given by $a^{-1} = a^{254}$ because any non zero element of $GF(2^8)$ satisfies $a = a^{256}$. (The inverse element of zero is usually defined to be zero.) The basic idea underlying the tower field approach is reduction of hardware cost by exploiting smaller arithmetic operations over subfield $GF((2^2)^2)$ or $GF(2^4)$ instead of $GF(2^8)$. There is a one-to-one map** (i.e., an isomorphism) between the elements of $GF(2^8)$ and those of the tower field. This GF inversion over a tower field is efficiently implemented in the Itoh-Tsujii Algorithm (ITA) [7].

Fig. 1.

Inversion circuit over $GF(((2^2)^2)^2)$ in [3].

Figure 1 illustrates a $GF(2^8)$ inversion circuit presented in [3], where the datapath is divided into upper and lower 4 bits and each component denotes an arithmetic circuit over subfield $GF((2^2)^2)$. Let $a \in GF(((2^2)^2)^2)$ be the input given by $h \alpha ^{16} + l \alpha$ in an NB $\{\alpha ^{16}, \alpha \}$, where h and l $(\in GF((2^2)^2))$ are respectively the upper and lower 4 bits of a, and $\alpha$ is a root of a second degree irreducible polynomial over $GF((2^2)^2)$ (i.e., a modular polynomial for extending $GF((2^2)^2)$ to $GF(((2^2)^2)^2)$). The inversion of a is calculated in the following three stages: (1) Calculation of the 16th and 17th powers, (2) Subfield inversion, and (3) Final multiplication. Note that the above $GF((2^2)^2)$ operators are replaced with the $GF(2^4)$ operators in the case of the tower field $GF((2^4)^2)$.

The performance of this inversion circuit depends on the tower field and its basis representation. Three of the best known circuit structures are based on the tower field of $GF(((2^2)^2)^2)$. Satoh and Morioka first designed this kind of $GF(((2^2)^2)^2)$ inversion circuit using PB [14]. Canright then designed a more compact circuit based on NB [3]. The hardware cost of inversion and exponentiation operations can be reduced by NB because the squaring operation is performed solely by wiring. Nogami et al. presented the possibility of MB, which employs both polynomial and normal bases for the input and output data, respectively [11]. Their method exhibited improved performance in the product of gate count and critical delay for the $GF(((2^2)^2)^2)$ inversion circuit and the AES S-Box, including isomorphic map**s. In addition to $GF(((2^2)^2)^2)$, it is possible to design efficient inversion circuits using another tower field of $GF((2^4)^2)$. Rudra et al. [13] and Jeon et al. [8] designed $GF((2^4)^2)$ inversion circuits based on PB with smaller critical delay than those of $GF(((2^2)^2)^2)$ inversion circuits.

2.2 Redundant Representations for Galois Fields

Polynomial Ring Representation (PRR). is a redundant representation of GF [5] An extension field $GF(2^m)$ based on a PB has a set of elements (i.e., polynomials) whose degrees are at most $m-1$ (i.e., m bits). Elements of an NB-based $GF(2^m)$ are also represented by m bits. On the other hand, an extension field $GF(2^m)$ based on PRR has a set of polynomials whose degrees are up to $n-1$ (i.e., n bits), where $n > m$ [5]. In other words, whereas a PB- or an NB-based $GF(2^m)$ is defined as an m-dimensional linear space over GF(2), a PRR-based $GF(2^m)$ is defined as an m-dimensional subspace of an n-dimensional linear space. PRR is also equivalent to Cyclic Redundancy Code (CRC), a kind of error-correction code.

Let x and H(x) be an indeterminate element and an irreducible polynomial over GF(2), respectively. Let G(x) be a polynomial of degree $n - m$, which is relatively prime to H(x), and is satisfied with $G(0) \not = 0$. Let P(x) be a polynomial (of degree n) given by the product of G(x) and H(x). A set of polynomials of degrees less than or equal to $n - 1$, where each polynomial is divisible by G(x), together with modulo P(x) arithmetic is isomorphic to $GF(2^m)$. Note here that $n = m + \deg G(x)$. The representation of $GF(2^m)$ using such a residue ring is called PRR. A PRR can be constructed from any PB-based $GF(2^m)$. (See Appendix for a construction method and corresponding example).

Table 1. Example of correspondence between PB- and PRR-based $GF(2^4)$.

Table 1 shows an example of elements for a PB-based $GF(2^4)$ and a constructed PRR-based $GF(2^4)$, where $\beta$ and x are the indeterminate elements of PB and PRR, respectively. Note that whereas the PB-based $GF(2^4)$ represents elements by at most third degree polynomials (i.e., 4 bits), the PRR-based $GF(2^4)$ represents elements by up to the fourth degree polynomial (i.e., 5 bits). It is known that the performance of the GF circuit generally improves as the number of terms in the modular polynomial decreases [17]. Here, a binomial $x^n + 1$ is available for the modular polynomial of PPR-based $GF(2^m)$, whereas it is unavailable for GFs based on non-redundant representations. This is because the modular polynomial P(x) is given by a reducible polynomial (i.e., $G(x) \times H(x)$). Thus, the performance of PRR-based GF arithmetic circuits can be better than those of PB- and NB-based arithmetic circuits. For example, we can use $x^{m+1} + 1$ for P(x) if the m-th degree All One Polynomial (AOP) is irreducible according to the following formula over GF(2):

$$\begin{aligned} x^{m+1} + 1 = (x+1)(x^m+x^{m-1}+ \dots +1), \end{aligned}$$

(1)

where the polynomial $x^m+x^{m-1}+ \dots +1$ is called the m-th degree AOP.

The major advantages of using the binomial are as follows: (i) Parallel multiplication can be given as the discrete time Wiener-Hopf equation, and (ii) Squaring and a part of constant multiplication are performed only by bitwise permutation (i.e., wiring). This suggests that the PRR-based design can be more efficient than conventional designs.

Redundantly Represented Basis (RRB). is another redundant representation of GF [10]. Each element is represented by a root of an m-th degree irreducible polynomial, similarly to PB and NB.

RRB is available when the m-th degree AOP is irreducible. Let $\beta$ be a root of the AOP. The m elements (i.e., bases) $\beta ^{m-1}, \beta ^{m-2}, \dots ,$ and $\beta ^0$ are linearly independent and then compose a PB. In contrast, RRB employs a binomial $\beta ^{m+1}-1$ as the modular polynomial, which is satisfied with the following equation:

$$\begin{aligned} \beta ^{m+1} - 1 = (\beta + 1) (\beta ^{m} + \beta ^{m-1} + \dots + 1) = 0. \end{aligned}$$

(2)

The set $\{\beta ^m, \beta ^{m-1}, \dots , \beta ^0\}$ is called RRB. Because the degree of the binomial is $m+1$, each element is represented by a linear combination of $\beta ^m, \beta ^{m-1}, \dots$ and $\beta ^0$. Note that the elements of such an RRB-based $GF(2^m)$ are represented in a non-unique manner because $\beta ^m, \beta ^{m-1}, \dots$ and $\beta ^0$ are linearly dependent¹.

RRB-based $GF(2^m)$ squaring can be performed by bitwise permutation, as is the case with NB. This is because RRB is equivalent to an extended (Type-I) Optimal Normal Basis (ONB). We can derive RRB by adding a base $\{1\}$ $(= \{\beta ^0\})$ to ONB. This means that an efficient multiplication method for ONB, called the Cyclic Vector Multiplication Algorithm (CVMA) [12], is also available for RRB. Thus, we can design more compact and efficient multipliers by combining RRB and CVMA. As an example, let us consider a $GF(2^4)$ multiplier based on RRB. Let s and t $(\in GF(2^4))$ be the inputs and u $(\in GF(2^4))$ be the output. Let $\beta$ be a root of the fourth degree AOP. In RRB, s is given by $s_4\beta ^4+s_3\beta ^3+ \dots + s_0$, where $s_0, s_1, \dots ,$ and $s_4 \in GF(2)$. (t and u are also given in the same manner.) The multiplication is represented by

$$\begin{aligned} u = s \times t = u_4\beta ^4 + u_3 \beta ^3 + u_2\beta ^2 + u_1 \beta + u_0, \end{aligned}$$

(3)

where

$$\begin{aligned} u_0= & {} (s_1 + s_4)(t_1+t_4) + (s_2+s_3)(t_2+t_3), \end{aligned}$$

(4)

$$\begin{aligned} u_1= & {} (s_0 + s_1)(t_0+t_1) + (s_2+s_4)(t_2+t_4), \end{aligned}$$

(5)

$$\begin{aligned} u_2= & {} (s_0 + s_2)(t_0+t_2) + (s_3+s_4)(t_3+t_4), \end{aligned}$$

(6)

$$\begin{aligned} u_3= & {} (s_0 + s_3)(t_0+t_3) + (s_1+s_2)(t_1+t_2), \end{aligned}$$

(7)

$$\begin{aligned} u_4= & {} (s_0 + s_4)(t_0+t_4) + (s_1+s_3)(t_1+t_3). \end{aligned}$$

(8)

The critical delay of such an RRB-based multiplier is $T_A + 2T_X$, while those of multipliers based on non-redundant representations are $T_A + 3T_X$ [10]. The gate count of the RRB-based multiplier requires only 10 AND and 25 XOR gates [10], whereas that of a PRR-based multiplier requires 25 AND and 20 XOR gates [5]. Nekado et al. [10] designed a more efficient $GF((2^4)^2)$ inversion circuit based on RRB by utilizing the above advantage.

3 Proposed $GF(2^8)$ Inversion Circuit

This section presents our proposed $GF(2^8)$ inversion circuit that takes full advantage of the above redundant GF arithmetic. The important ideas are to employ the tower field $GF((2^4)^2)$ inside the circuit and perform the subfield (i.e., $GF(2^4)$) operations using redundant GF arithmetic. We introduce PRR for the $GF(2^4)$ inversion because we can exploit a modular polynomial, $P(x) = x^5 + 1$, thanks to the irreducible fourth degree AOP. We also introduce RRB for the $GF(2^4)$ multiplication. In addition, we employ an NB for the input in order to exploit the Frobenius map** feature, which performs the 16th power of input solely by wiring.

Fig. 2.

Proposed inversion circuit.

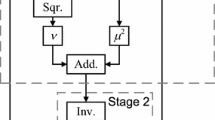
In accordance with ITA, our inversion circuit consists of three stages, as shown in Fig. 1. Here, we represent the inputs of Stages 1, 2, and 3 by NB, PRR, and RRB, respectively. In particular, we employ an NB that has a symmetric property, which makes it possible to convert the elements from NB to PRR without increasing the circuit delay.

Figure 2 shows a block diagram of our proposed circuit, where components H, L,  and F respectively calculate $H_{i, j}, L_{i, j},$ and $F_{i', j'}$ described in the following. When input a is represented by $h\alpha ^{16} + l\alpha$, components NBtoRRB convert h and l from NB to RRB solely by wiring. Note that H and L are shared with Stages 1 and 3. The stages in the proposed circuit are designed as follows:

1. Calculation of the 16th and 17th powers.

Stage 1 performs the 16th and 17th powers of input, where input a is given by NB, and outputs $a^{16}$ and $a^{17}$ are given by RRB and PRR, respectively. Let $\alpha$ be a root of a second degree irreducible polynomial over $GF(2^4)$. The irreducible polynomial is given by $\alpha ^2+\mu \alpha +\nu$, where $\mu$ and $\nu$ are the constants of $GF(2^4)$. When input a is represented by $a = h\alpha ^{16} + l \alpha$ in an NB $\{\alpha ^{16}, \alpha \}$, $a^{16}$ and $a^{17}$ are respectively given by

$$\begin{aligned} a^{16}= & {} l \alpha ^{16} + h \alpha , \end{aligned}$$

(9)

$$\begin{aligned} a^{17}= & {} hl \mu ^2 + (h+l)^2 \nu . \end{aligned}$$

(10)

Equation (9) indicates that $a^{16}$ is performed by twisting wires.

The isomorphic map** from NB to RRB does not require any additional gates because the NB (e.g., $\{\beta ^4, \beta ^3, \beta ^2, \beta ^1\}$) can be considered as a reduced version of RRB (e.g., $\{\beta ^4, \beta ^3, \beta ^2, \beta ^1, \beta ^0\}$) with the same root of the 4th degree AOP. Conversely, the isomorphic map** from NB to PRR requires some gates. However, the symmetric property of the NB used in our circuit provides a map** that does not increase the circuit delay.

Let us now look at the isomorphic map** from NB to PRR. Here, an isomorphic map** is represented by $z' = \varGamma (z)$, where an element z in one GF representation is converted into an element $z'$ in another GF representation. In the binary vector form, the output $\varvec{z}'$ is obtained from the product of a conversion matrix $\gamma$ and the transposed input (i.e., $\varvec{z}' = \gamma \varvec{z}^T$) when the conversion matrix $\gamma$ represents the isomorphism $\varGamma$. The PRR-based $GF(2^4)$ is given with the modular polynomial $P(x) = x^5 + 1$ ($G(x) = x + 1$ and $H(x) = x^4 + x^3 + x^2 + x + 1$) and the conversion matrix from NB to PRR is as follows:

$$\begin{aligned} \phi = \left( \begin{matrix} 1 &{} 1 &{} 1 &{} 1 \\ 0 &{} 1 &{} 1 &{} 1 \\ 1 &{} 0 &{} 1 &{} 1 \\ 1 &{} 1 &{} 0 &{} 1 \\ 1 &{} 1 &{} 1 &{} 0 \end{matrix}\right) , \end{aligned}$$

(11)

where the least significant bits are in the upper left corner. (See Appendix for an explanation of how to obtain the matrix.) Let d $(= d_4x^4 +d_3x^3 + \dots +d_0)$ be the output of Stage 1 (i.e., the 17th power of input in PRR), where $d_0, d_1, \dots ,$ and $d_4$ are the elements of GF(2). The output is provided by applying the isomorphism $\varPhi$ from NB to PRR to $a^{17}$ (i.e., the product of the conversion matrix $\phi$ and the transposed vector form of $a^{17}$). However, the multiplication of $\phi$ and the output of Eq. (10) requires an additional circuit with $2T_X$ delay if the multiplication is performed explicitly. To avoid such additional circuit, we derive another output equation from Eq. (10) as follows:

$$\begin{aligned} d= & {} \varPhi (hl \mu ^2 + (h+l)^2 \nu ) \nonumber \\= & {} \varPhi (\mu ^2(hl)) + \varPhi (\nu ((h+l)^2)) \nonumber \\= & {} \varPhi '(hl) + \varPhi ''((h+l)^2), \end{aligned}$$

(12)

where $\varPhi '$ and $\varPhi ''$ are the linear functions obtained by merging $\varPhi$ with the constant multiplications of $\mu ^2$ and $\nu$, respectively. Note that constant multiplications over GF can also be given as linear functions represented by conversion matrices. When $\mu = \beta ^4+\beta$ and $\nu = \beta$, the resulting matrices $\phi '$ and $\phi ''$ representing respectively $\varPhi '$ and $\varPhi ''$ are given as

$$\begin{aligned} \phi ' = \left( \begin{matrix} 0 &{} 1 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 &{} 1 \\ 0 &{} 0 &{} 0 &{} 1 \\ 1 &{} 0 &{} 0 &{} 0 \\ 1 &{} 1 &{} 0 &{} 0 \end{matrix}\right) , \ \phi '' = \left( \begin{matrix} 1 &{} 1 &{} 1 &{} 0 \\ 1 &{} 1 &{} 1 &{} 1 \\ 0 &{} 1 &{} 1 &{} 1 \\ 1 &{} 0 &{} 1 &{} 1 \\ 1 &{} 1 &{} 0 &{} 1 \end{matrix}\right) , \end{aligned}$$

(13)

where the least significant bits are in the upper left corners. The resulting elements of PRR are shown in Table 1.

To design the circuit defined by Eq. (12), we exploit an NB with the symmetric property that h and l are given by $h = h_4\beta ^4+h_3\beta ^3+h_2\beta ^2+h_1\beta$ and $l = l_4\beta ^4+l_3\beta ^3+l_2\beta ^2+l_1\beta$ with a common NB $\{\beta ^4, \beta ^3, \beta ^2, \beta ^1\}$, where $h_1, \dots , h_4$ and $l_1, \dots , l_4$ are the elements of GF(2) ². As a result, the outputs $d_0, d_1, \dots ,$ and $d_4$ are given by

$$\begin{aligned} d_0= & {} (h_1l_2 + h_2l_1 + h_3l_4 + h_4l_3 + h_1l_1+h_4l_4)\nonumber \\&+ (h_1+l_1+h_3+l_3+h_4+l_4), \end{aligned}$$

(14)

$$\begin{aligned} d_1= & {} (h_1l_2 + h_2l_1 + h_1l_3 + h_3l_1 + h_2l_2+h_4l_4) \nonumber \\&+ (h_1+l_1+h_2+l_2+h_3+l_3+h_4+l_4), \end{aligned}$$

(15)

$$\begin{aligned} d_2= & {} (h_1l_3 + h_3l_1+h_1l_4 + h_4l_1 +h_2l_3+h_3l_2 + h_2l_2)\nonumber \\&+ (h_1+l_1+h_2+l_2+h_4+l_4), \end{aligned}$$

(16)

$$\begin{aligned} d_3= & {} (h_1l_4 + h_4l_1 + h_2l_3+h_3l_2+h_2l_4 + h_4l_2 + h_3l_3) \nonumber \\&+ (h_2+l_2+h_3+l_3+h_4+l_4), \end{aligned}$$

(17)

$$\begin{aligned} d_4= & {} (h_2l_4 + h_4l_2 +h_3l_4 + h_4l_3 + h_1l_1+h_3l_3) \nonumber \\&+ (h_1+l_1+h_2+l_2+h_3+l_3), \end{aligned}$$

(18)

respectively. Here, the symmetric property enable us to factor Eqs. (14)–(18) as follows:

$$\begin{aligned} d_0= & {} H_{1, 2}\vee L_{1, 2} + H_{3, 4}\vee L_{3, 4} + h_2 \vee l_2+h_3l_3, \end{aligned}$$

(19)

$$\begin{aligned} d_1= & {} H_{1, 2} \vee L_{1, 2} + H_{1, 3}L_{1, 3}+ h_3 \vee l_3+h_4 \vee l_4, \end{aligned}$$

(20)

$$\begin{aligned} d_2= & {} H_{1, 3} \vee L_{1, 3} +H_{1, 4}L_{1, 4} + H_{2, 3}\vee L_{2, 3} +h_4 \vee l_4, \end{aligned}$$

(21)

$$\begin{aligned} d_3= & {} H_{1, 4} \vee L_{1, 4} + H_{2, 3} \vee L_{2, 3} + H_{2, 4}L_{2, 4} + h_1 \vee l_1, \end{aligned}$$

(22)

$$\begin{aligned} d_4= & {} H_{2, 4} \vee L_{2, 4} + H_{3, 4} \vee L_{3, 4} + h_1 \vee l_1+h_2l_2, \end{aligned}$$

(23)

where $H_{i,j} = h_i+h_j$, $L_{i,j} = l_i+l_j$ $(1 \le i < j \le 4)$, and $\vee$ denotes the OR operator (i.e., $a \vee b = a+b+ab$). The component denoted by Stage 1 in Fig. 2 performs the computations corresponding to Eqs. (19)–(23). Therefore, the proposed Stage 1 is performed with only $T_A + 3T_X$ (or $T_O + 3T_X$) delay, whereas conventional $GF(((2^2)^2)^2)$ inversion implementations are performed with at least $6T_X$ delay, where $T_A, T_O,$ and $T_X$ denote the delays of the AND, OR, and XOR gates, respectively.

2. Subfield Inversion.

Stage 2 performs the inversion over the subfield $GF(2^4)$, where the input and output are given by PRR and RRB, respectively. We first describe the architecture of the PRR-based $GF(2^4)$ inversion, and then show the isomorphic map** from PRR to RRB below.

The inversion over $GF(2^4)$ is performed by the 14th power of the input. The input (i.e., the output of Stage 1) d $(= d_4x^4 + d_3x^3 + \dots + d_0)$ is given as an element of the PRR-based $GF(2^4)$. The input is satisfied with the condition (called the linear recurrence relation) $d_0 + d_1 + d_2 + d_3 + d_4 = 0$ ³ because it is equivalent to the codeword of a CRC generated by G(x) $(= x + 1)$, which makes it possible to perform the exponentiation by bitwise operations over the PRR-based $GF(2^4)$ in an efficient manner.

Let e $(= e_4x^4 + e_3x^3 + \dots + e_0)$ be the inverse element of d in PRR, where $e_0, e_1, \dots ,$ and $e_4$ are the elements of GF(2). Using the linear recurrence relation, we can derive $e_0, e_1, \dots ,$ and $e_4$ as follows:

$$\begin{aligned} e_0= & {} (d_1 \vee d_4)(d_2 \vee d_3), \end{aligned}$$

(24)

$$\begin{aligned} e_1= & {} ((d_4+1)(d_1+d_2)) \vee (d_0d_4(d_2 \vee d_3)), \end{aligned}$$

(25)

$$\begin{aligned} e_2= & {} ((d_3+1)(d_2+d_4)) \vee (d_0d_3(d_1 \vee d_4)), \end{aligned}$$

(26)

$$\begin{aligned} e_3= & {} ((d_2+1)(d_1+d_3)) \vee (d_0d_2(d_1 \vee d_4)), \end{aligned}$$

(27)

$$\begin{aligned} e_4= & {} ((d_1+1)(d_3+d_4)) \vee (d_0d_1(d_2 \vee d_3)). \end{aligned}$$

(28)

According to Eqs. (24)–(28), the proposed Stage 2 requires $T_A + T_O + T_X$ delay, whereas the conventional structures [3, 10, 11, 14] require at least $T_A+3T_X$. Note that when the multiplicative unit element E(x) $(= x^4 + x^3 + x^2 + x)$ is given as the input, the output becomes not E(x) but 1. However, the output is acceptable in Stage 3 (i.e., $GF(2^4)$ multiplication) because both E(x) and 1 are the idempotent elements in the residue ring modulo P(x).

Let us now look at the PRR-to-RRB map**. To provide it uniquely, we focus on the definition of PRR in [5], in which the map** $\varPsi$ from PRR defined by x to another representation defined by $\beta$ is isomorphism. Let f $(= f_4\beta ^4+f_3\beta ^3+ \dots + f_0)$ be the output of Stage 2 in RRB, where $f_0, f_1, \dots ,$ and $f_4$ are the elements of GF(2). The output can be given by

$$\begin{aligned} f = \varPsi (e) = e_4\beta ^4+e_3\beta ^3+e_2\beta ^2+e_1\beta +e_0. \end{aligned}$$

(29)

This means that the PRR-to-RRB map** is performed without any additional circuit, assuming that $f_0 = e_0, \dots ,$ and $f_4=e_4$. As a result, the PRR-based design provides inversion and isomorphic map** with fewer logic gates.

3. Final multiplication.

Stage 3 generates the final output using two $GF(2^4)$ multiplication operations, where both the inputs and output are given by RRB. As stated above, the RRB-based $GF(2^4)$ multiplier is known to be one of the most efficient multipliers [10].

Let $h'$ $(= h'_4\beta ^4+h'_3\beta ^3+\dots +h'_0)$ be the upper 5 bits of the final output $a^{-1}$ in RRB, where $h'_0, h'_1, \dots ,$ and $h'_4$ are the elements of GF(2). Multiplying f and l, we can calculate elements $h'_0, h'_1, \dots ,$ and $h'_4$ as follows:

$$\begin{aligned} h'_0= & {} L_{1, 4}F_{1, 4} + L_{2, 3}F_{2, 3}, \end{aligned}$$

(30)

$$\begin{aligned} h'_1= & {} l_1F_{0, 1} + L_{2, 4}F_{2, 4}, \end{aligned}$$

(31)

$$\begin{aligned} h'_2= & {} l_2F_{0, 2} + L_{3, 4}F_{3, 4}, \end{aligned}$$

(32)

$$\begin{aligned} h'_3= & {} l_3F_{0, 3} + L_{1, 2}F_{1, 2}, \end{aligned}$$

(33)

$$\begin{aligned} h'_4= & {} l_4F_{0, 4} + L_{1, 3}F_{1, 3}, \end{aligned}$$

(34)

where $F_{i',j'}$ denotes $f_{i'} + f_{j'}$ $(0 \le i' < j' \le 4)$. The lower five bits of $a^{-1}$ (denoted by $l'$) are also obtained in the same manner as in Eqs. (30)–(34). The component denoted by Stage 3 in Fig. 2 performs the computations corresponding to Eqs. (30)–(34). Note here that the calculations for $F_{i', j'}$ can be shared within Stage 3. As a result, the number of circuit components for the two multipliers in Stage 3 is reduced.

4 Performance Evaluation

Table 2 shows the circuit delay and gate count of the proposed inversion circuit, where $(g_0, g_1, g_2, g_3, g_4, g_5, g_6)$ in the Gate count column respectively indicate the number of AND, OR, XOR, XNOR, NOT, NAND and NOR gates, and Rep. indicates the GF representation(s) used in the circuit. For comparison, the table also shows those of the conventional inversion circuits. The critical delay paths of all the conventional ones were given by reference to [10]. On the other hand, the gate counts of the conventional ones were individually given because there was no single reference data covering all the conventional ones. The gate count of [3] was given from the original paper [3], that of [14] was given from a public source code by the authors [15], and those of [8, 10, 13] were given by reference to [10]. The gate count of [11] was given from a straightforward structure designed by us according to [11] because there was no public data and source code.

The critical paths of Stages 1, 2, and 3 in the proposed circuit require $T_A +3T_X$, $T_A +T_O +T_X$, and $T_A +2T_X$ delay, respectively. As a result, the total delay of our inversion circuit is $3T_A+T_O+6T_X$, which compared with the other inversion circuits, is the smallest. The gate count in this work is smaller or comparable to the conventional ones. In total, our circuit is more efficient than any other circuits because fewer XOR and XNOR gates are required compared to the other implementations.

Table 2. Critical delay and gate count of inversion circuits over tower fields.

Table 3. Performance evaluation of inversion circuits over tower fields.

To conduct a detailed evaluation, some of the above $GF(2^8)$ inversion circuits were synthesized using Synopsys Design Compiler with a TSMC 65 nm CMOS standard cell library. Table 3 shows the synthesis results, where Area indicates the circuit area estimated based on a two-way NAND equivalent gate size (i.e., gate equivalents (GE)), Time indicates the circuit delay under the worst-case conditions, and Area-Time product indicate the product of Area and Time. For the best performance comparison, an area optimization option (which maximizes the effort of minimizing the number of gates without flattening the description) was applied. Note that the results were consistent even when the following speed optimization (which searches for the minimum timing without increasing the area obtained from the prior area optimization) options was applied. The conventional inversion circuits were also synthesized using the same option. The source codes of [3, 14] were obtained from authors’ websites [4, 15], respectively. (Like them, we also applied gate-reduction techniques to our inversion circuit.) The source codes of [10, 11] were described by us according to the structures given in the papers. Consequently, we confirmed that the proposed circuit achieves the smallest area of 229.67 GE and the smallest circuit delay of 1.81 ns. The area-time product of the proposed circuit is 19.3 % smaller than that of the conventional best circuit.

5 Application to AES S-Box

The proposed inversion circuit was efficiently applied to the AES S-Box design. The AES S-Box consists of a $GF(2^8)$ inversion and an affine transformation over GF(2). Here, the $GF(2^8)$ is represented in a PB and the $GF(2^8)$ inversion is performed with an irreducible polynomial $x^8 + x^4 + x^3 + x + 1$. Therefore, an isomorphic map** between $GF(2^8)$ and $GF((2^4)^2)$ is required if the inversion over $GF((2^4)^2)$ is applied. Figure 3 shows an overview of the AES S-Box with tower field arithmetic. The input (in the PB-based $GF(2^8)$) is initially mapped to the tower field by applying an isomorphic map** $\varDelta _f$. After the inversion operation over the tower field, the inverse map** and affine transformation are finally performed in series. Here, we can merge the inverse map** into the affine transformation because both of them are represented in the form of constant matrices over GF(2). The merged map** is denoted by $\varDelta _l$. This merging reduces the delay and gate counts.

Fig. 3.

Overview of AES S-Box based on tower field arithmetic.

The matrices for the map**s $\varDelta _f$ and $\varDelta _l$ have an impact on the performance of S-Box. When tower field $GF((2^4)^2)$ is used, the matrices are defined by the bases of $GF(2^4)$ and the modular polynomials for the extension of $GF(2^4)$ to $GF((2^4)^2)$. The efficiency of the two matrices for map**s $\varDelta _f$ and $\varDelta _l$ is determined by the largest Hamming weight in the columns. For example, if the largest Hamming weight in the columns is four, the critical path becomes $2T_X$ delay. If it is five, the critical path becomes $3T_X$ delay. Therefore, the matrices should be selected with a view to minimizing the largest Hamming weight in the columns.

In our design, we found efficient conversion matrices $\delta _f$ and $\delta _l$ respectively for $\varDelta _f$ and $\varDelta _l$ when the $GF(2^4)$ elements of Stage 1 are represented in an NB $\{\beta ^4, \beta ^3, \beta ^2, \beta ^1\}$ and the modular polynomial for the extension is given by $\alpha ^2+(\beta ^4+\beta )\alpha +\beta$. As an example, the matrices $\delta _f$ and $\delta _l$ are given by

$$\begin{aligned} \delta _f = \left( \begin{matrix} 0 &{} 1 &{} 0 &{} 1 &{} 1 &{} 1 &{} 0 &{} 0 \\ 1 &{} 0 &{} 1 &{} 0 &{} 0 &{} 0 &{} 1 &{} 1 \\ 1 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} 0 &{} 1 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 \\ 0 &{} 1 &{} 1 &{} 0 &{} 1 &{} 1 &{} 0 &{} 0 \\ 1 &{} 0 &{} 1 &{} 0 &{} 1 &{} 0 &{} 0 &{} 0 \\ 1 &{} 1 &{} 1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 \\ 0 &{} 0 &{} 1 &{} 1 &{} 0 &{} 0 &{} 0 &{} 1 \end{matrix} \right) , \,\delta _l = \left( \begin{matrix} 1 &{} 1 &{} 1 &{} 1 &{} 0 &{} 1 &{} 0 &{} 0 &{} 1 &{} 0\\ 0 &{} 0 &{} 1 &{} 1 &{} 0 &{} 1 &{} 1 &{} 1 &{} 0 &{} 1\\ 1 &{} 1 &{} 1 &{} 1 &{} 0 &{} 0 &{} 1 &{} 0 &{} 1 &{} 0\\ 1 &{} 0 &{} 0 &{} 0 &{} 1 &{} 1 &{} 1 &{} 1 &{} 0 &{} 1\\ 1 &{} 1 &{} 0 &{} 1 &{} 1 &{} 1 &{} 0 &{} 0 &{} 0 &{} 1\\ 1 &{} 0 &{} 0 &{} 0 &{} 1 &{} 1 &{} 0 &{} 1 &{} 1 &{} 1\\ 0 &{} 0 &{} 1 &{} 0 &{} 1 &{} 0 &{} 0 &{} 1 &{} 0 &{} 1\\ 1 &{} 0 &{} 1 &{} 0 &{} 0 &{} 1 &{} 1 &{} 0 &{} 1 &{} 1 \end{matrix} \right) , \end{aligned}$$

(35)

where the least significant bits are in the upper left corners. Here, the largest Hamming weight in the columns of $\delta _f$ is at most four while that of $\delta _l$ is at most six. This means that the former and latter map**s are implemented with delays of $2T_X$ and $3T_X$, respectively. Note that the matrix $\delta _l$ does not include the constant addition of affine transformation in S-Box. The addition does not lead to the increase of delay for our S-Box since the largest Hamming weight of in the columns is at most six.

Table 4. Performance comparison of AES S-Boxes based on tower field arithmetic.

Table 4 shows the critical delay of the proposed AES S-Box compared with the conventional implementations. Our circuit achieves $3T_A + T_O + 11T_X$ delay, which is smaller than the conventional S-Boxes with tower field arithmetic. The table also shows the synthesis results (area, delay time, and power) obtained from the same tool and synthesis options as the above⁴. The source codes were given from the same methods as Table 3. Note here that Canright’s design in [3] supports both encryption and decryption, and we have slightly changed it to support only encryption to allow a fair comparison to our design. As a result, the area-time product of our AES S-Box is more than 22.5 % better than Canright’s S-Box, which had been the most efficient for a long time, and more than 17.1 % better than Nekado’s latest S-Box.

A further evaluation with full AES implementations is being left for the future study. For example, our current design does not directly lead to the most efficient one if we should support both encryption and decryption. For such evaluation, another optimization (e.g. considering the overall architecture and conversion matrices specified for both encryption and decryption) should be discussed. On the other hand, the practical impact of the proposed method would be even more visible in that case.

Another discussion point when applying the proposed method to cryptographic cores is the well-known side channel issue. In particular, the resource sharing of Stages 1 and 3 would cause glitches during the computation. To apply our method to pipelining-based countermeasures for reducing glitch problems, we need to decompose shared resources, which results in the increase of 12 XOR gates in total. Note however that such increase would also happen in other works (e.g., [3, 10]) using the similar optimization. In contrast, our method is more suitable for multiplexing-based countermeasures, such as WDDL, due to the high efficiency. A further and comprehensive study on the side-channel security is definitely one of the important future topics for our method.

6 Conclusion

This paper proposed a new $GF(2^8)$ inversion circuit that utilizes a combination of non-redundant and redundant GF arithmetic. The proposed circuit, which is based on tower field arithmetic, was designed by utilizing PRR and RRB for the subfield inversion and multiplication, respectively. The flexibility of such redundant representations can provide efficient isomorphic map**s from/to $GF(2^8)$. The efficiency of our proposed inversion circuit and its AES encryption S-Box was evaluated by gate count and logic synthesis results with a 65 nm CMOS standard cell library. As a result, we confirmed that the proposed inversion circuit is approximately 38 % faster than the conventional best $GF(((2^2)^2)^2)$ circuit without any area overhead. Further, even including isomorphic map**s to AES GF, the proposed circuit exhibited the best efficiency compared with existing inversion circuits based on tower field arithmetic.

Redundant GF representations, such as PRR and RRB, provide high flexibility for GF arithmetic circuit design. It is definitely possible to obtain efficient circuit structures using them because the search space of isomorphic map**s increases as a result of their flexibility. In addition, a combination of non-redundant and redundant GF representations has the potential to further improve GF circuits, as shown in this paper. On the other hand, our AES S-Box design is optimized only for the encryption. If an AES design should support both encryption and decryption, our current design does not directly lead to the most efficient one. In that case, another specific optimization for the overall architecture and conversion matrices for both encryption and decryption should be considered. An isomorphic map** optimization method for other applications still remains as future work. Further research is being conducted to expand the application of our design methodology. Other block ciphers and error-correction circuits, including GF inversion circuits, are possible applications. It is also worth considering efficient implementation of countermeasures against side-channel attacks by redundant GF arithmetic.

Appendix: Construction Method of PRR and Its Example

Construction of an isomorphic map** from a PB-based $GF(2^m)$ to a PRR-based $GF(2^m)$ is accomplished as follows. We first define the multiplicative unit element of PRR for the construction. Let U(x) and V(x) be polynomials that satisfy

$$\begin{aligned} U(x)G(x) + V(x)H(x) = 1. \end{aligned}$$

(36)

H(x) is an irreducible polynomial of the PB-based $GF(2^m)$ and G(x) is a polynomial of degree $n - m$, which is relatively prime to H(x). Such U(x) and V(x) are always found since G(x) and H(x) are relatively prime. We can easily derive them using the extended Euclidean algorithm. The multiplicative unit element E(x), which is an idempotent of the PRR-based $GF(2^m)$, is given by U(x)G(x). This is explained by multiplying Eq. (36) and U(x)G(x) as follows:

$$\begin{aligned} \{U(x)G(x)\}^2 + U(x)G(x)V(x)H(x) = U(x)G(x). \end{aligned}$$

(37)

Therefore,

$$\begin{aligned} \{E(x)\}^2 \equiv E(x) \text { mod }P(x), \end{aligned}$$

(38)

where $P(x) = G(x)H(x)$. Note that V(x)H(x) is not included in the PRR-based $GF(2^m)$ because V(x)H(x) is indivisible by G(x).

With the above relations, we obtain the relational expression between the indeterminate elements of PB and PRR. Let $\beta$ be a root of H(x) (i.e., $H(\beta ) = 0$). The multiplication of Eq. (36) and x is given as follows:

$$\begin{aligned} xU(x)G(x) + xV(x)H(x) = x. \end{aligned}$$

(39)

Assuming that we substitute $\beta$ for x in Eq. (39), both LHS and RHS become $\beta$. This means that $\beta$ is mapped to/from $x \times E(x)$. We also obtain the corresponding relational expressions between $\beta ^i$ and $x^i \times E(x)$ for an integer i $(0 \le i \le m -~1)$. As a result, we can construct the isomorphic map** using the relational expressions. Let $C_i(x)$ be an element of the PRR-based $GF(2^m)$ corresponding to $\beta ^i$. $C_i(x)$ is then given by

$$\begin{aligned} C_{i}(x) \equiv x^{i} \times E(x) \text { mod }P(x). \end{aligned}$$

(40)

Note that $C_0(x), C_1(x), \dots ,$ and $C_{m-1}(x)$ are linearly independent in the polynomial ring over GF(2) because $\{\beta ^{m-1}, \beta ^{m-2}, \dots , \beta ^0\}$ composes a PB of $GF(2^m)$. Therefore, the conversion matrix $\phi _{PB \rightarrow PRR}$ for the isomorphic map** from PB- to PRR-based $GF(2^m)$ is given by

$$\begin{aligned} \phi _{PB\rightarrow PRR} = \left( \begin{matrix} {{\varvec{c}}}_0^T&{{\varvec{c}}}_1^T&\dots&{{\varvec{c}}}_{m-1}^T \end{matrix}\right) , \end{aligned}$$

(41)

where $\varvec{c}_i^T$ denotes the transposed binary vector form of $C_i(x)$. The least significant bits are in the upper left corner.

As an example of PRR, we present the construction of a PRR-based $GF(2^4)$. Here, the modular polynomial P(x) is given by $x^5 + 1$ and its factors G(x) and H(x) are given by

$$\begin{aligned} G(x)= & {} x+1, \end{aligned}$$

(42)

$$\begin{aligned} H(x)= & {} x^4+x^3+x^2+x+1. \end{aligned}$$

(43)

We first compute the multiplicative unit element E(x), which is derived from G(x) and H(x) by using the extended Euclidean algorithm as follows:

$$\begin{aligned} (x^3+x) \times G(x) + 1 \times H(x) = 1. \end{aligned}$$

(44)

Therefore, $E(x) = (x^3+x) \times G(x) = x^4+x^3+x^2+x$. $C_0(x), C_1(x), C_2(x)$ and $C_3(x)$ are then obtained as follows:

$$\begin{aligned} C_0(x)= & {} x^4+x^3+x^2+x, \end{aligned}$$

(45)

$$\begin{aligned} C_1(x)= & {} x^4+x^3+x^2+1, \end{aligned}$$

(46)

$$\begin{aligned} C_2(x)= & {} x^4+x^3+x+1, \end{aligned}$$

(47)

$$\begin{aligned} C_3(x)= & {} x^4+x^2+x+1, \end{aligned}$$

(48)

which correspond to $\beta ^0, \beta ^1, \beta ^2$ and $\beta ^3$, respectively. Thus, a conversion matrix $\phi _{PB\rightarrow PRR}$ from the PB-based $GF(2^4)$ with $H(\beta )$ to a PRR-based $GF(2^4)$ with P(x) is given by

$$\begin{aligned} \phi _{PB\rightarrow PRR} = \left( \begin{matrix} 0 &{} 1 &{} 1 &{} 1 \\ 1 &{} 0 &{} 1 &{} 1 \\ 1 &{} 1 &{} 0 &{} 1 \\ 1 &{} 1 &{} 1 &{} 0 \\ 1 &{} 1 &{} 1 &{} 1 \end{matrix}\right) , \end{aligned}$$

(49)

where the least significant bits are in the upper left corner. The conversion matrix $\phi _{NB}$ from the NB-based $GF(2^4)$ with $H(\beta )$ to the PRR-based $GF(2^4)$ is also constructed by using the NB $\{\beta ^4, \beta ^3, \beta ^2, \beta ^1\}$. $\phi _{NB\rightarrow PRR}$ is given by

$$\begin{aligned} \phi _{NB\rightarrow PRR} = \left( \begin{matrix} 1 &{} 1 &{} 1 &{} 1 \\ 0 &{} 1 &{} 1 &{} 1 \\ 1 &{} 0 &{} 1 &{} 1 \\ 1 &{} 1 &{} 0 &{} 1 \\ 1 &{} 1 &{} 1 &{} 0 \end{matrix}\right) , \end{aligned}$$

(50)

where the least significant bits are in the upper left corner.