Abstract
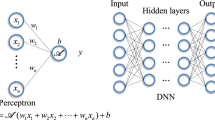
The finite element method (FEM) is a well-known method for numerically solving partial differential equations (PDEs) over a physical domain. It has been applied successfully to solve various problems in the field of structural analysis, electromagnetics, heat transfer, fluid flows, etc. However, the issue of improving FEM has been going on for the last 50 years. The objective of the study is to create an artificial neural network (ANN) model that can learn to predict the stiffness matrices of 2D finite elements, such as the 8-node quadrilateral element. The computational efficiency and accuracy of the finite elements generated through the ANN model are also checked with existing finite elements through some numerical examples. The results have been found to be consistent with available literature.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Cook RD, Malkus DS, Plesha ME, Witt RJ (2007) Concepts and applications of finite element analysis. John Wiley & Sons
Gautam SS, Khan K (2020) Detection of fretting fatigue using machine learning algorithms. In: Proceedings of the 3rd structural integrity conference and exhibition (SICE 2020)—“structural integrity at multiple length scales” (e-Conference). IIT Bombay
Glorot X, Bengio Y (2010) Understanding the difficulty of training deep feedforward neural networks. In: Proceedings of the thirteenth international conference on artificial intelligence and statistics. JMLR workshop and conference proceedings, pp 249–256
Goodfellow I, Bengio Y, Courville A (2016) Deep learning. MIT Press
Gouravaraju S, Narayan J, Sauer RA, Gautam SS (2023) A Bayesian regularization-backpropagation neural network model for peeling computations. J Adhesion 99(1):92–115
Hughes TJ (1980) Generalization of selective integration procedures to anisotropic and nonlinear media. Int J Numer Meth Eng 15(9):1413–1418
Ioffe S, Szegedy C (2015) Batch normalization: accelerating deep network training by reducing internal covariate shift. In: Bach F, Blei D (eds) Proceedings of the 32nd international conference on machine learning. Proceedings of machine learning research, vol 37. PMLR, Lille, France, pp 448–456
Jung J, Yoon K, Lee PS (2020) Deep learned finite elements. Comput Methods Appl Mech Eng 372:113401
Khoei A, Moslemi H, Seddighian M (2020) An efficient stress recovery technique in adaptive finite element method using artificial neural network. Eng Fract Mech 237:107231
Kingma DP, Ba J (2014) Adam: a method for stochastic optimization. ar**v preprint ar**v:1412.6980
Lagaris IE, Likas A, Fotiadis DI (1998) Artificial neural networks for solving ordinary and partial differential equations. IEEE Trans Neural Networks 9(5):987–1000
Liang L, Liu M, Martin C, Sun W (2018) A deep learning approach to estimate stress distribution: a fast and accurate surrogate of finite-element analysis. J R Soc Interface 15(138):20170844
Liu X, Athanasiou CE, Padture NP, Sheldon BW, Gao H (2020) A machine learning approach to fracture mechanics problems. Acta Mater 190:105–112
Mitchell T (1997) Machine learning. McGraw-Hill Education
Nowell D, Nowell P (2020) A machine learning approach to the prediction of fretting fatigue life. Tribol Int 141:105913
Oishi A, Yagawa G (2017) Computational mechanics enhanced by deep learning. Comput Methods Appl Mech Eng 327:327–351
Oishi A, Yagawa G (2020) A surface-to-surface contact search method enhanced by deep learning. Comput Mech 65:1125–1147
Ozarde AP, Narayan J, Yadav D, McNay GH, Gautam SS (2020) Optimization of diesel engine’s liner geometry to reduce head gasket’s fretting damage. SAE Int J Engines 14(1):81–97
Raissi M, Perdikaris P, Karniadakis GE (2019) Physics-informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J Comput Phys 378:686–707
Roylance D (2001) Transformation of stresses and strains. Lecture notes for mechanics of materials
Vithalbhai SK, Nath D, Agrawal V, Gautam SS (2022) Artificial neural network assisted numerical quadrature in finite element analysis in mechanics. Mat Today Proc 66:1645-1650
Vithalbhai S, Gautam SS (2021) A machine learning approach to fretting fatigue problem. In: Proceedings of the international conference on futuristic technologies (e-Conference)—structural health monitoring, energy harvesting, Green Material and Biomechanics. IIT Delhi
Zienkiewicz OC, Taylor RL, Zhu JZ (2005) The finite element method: its basis and fundamentals. Elsevier
Acknowledgements
The authors gratefully acknowledge the support from SERB, DST under project IMP/2019/000276, and VSSC, ISRO, through MoU No.: ISRO:2020:MOU:NO: 480.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2023 The Author(s), under exclusive license to Springer Nature Singapore Pte Ltd.
About this paper
Cite this paper
Nath, S.S., Nath, D., Gautam, S.S. (2023). Design of Efficient Finite Elements Using Deep Learning Approach. In: Sharma, R., Kannojiya, R., Garg, N., Gautam, S.S. (eds) Advances in Engineering Design. FLAME 2022. Lecture Notes in Mechanical Engineering. Springer, Singapore. https://doi.org/10.1007/978-981-99-3033-3_2
Download citation
DOI: https://doi.org/10.1007/978-981-99-3033-3_2
Published:
Publisher Name: Springer, Singapore
Print ISBN: 978-981-99-3032-6
Online ISBN: 978-981-99-3033-3
eBook Packages: EngineeringEngineering (R0)