SpringerLink
Log in

Bi-Level Linear Fuzzy Fractional Programming Problem Under Trapezoidal Fuzzy Environment: A Solution Approach

  • Conference paper
  • First Online:
Proceedings of International Joint Conference on Advances in Computational Intelligence (IJCACI 2022)

Part of the book series: Algorithms for Intelligent Systems ((AIS))

  • 187 Accesses

Abstract

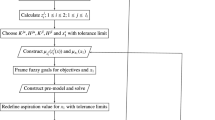
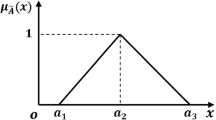
This paper proposes a method to solve a bi-level linear fuzzy fractional programming problem comprising all its constants and coefficients expressed in form of trapezoidal fuzzy numbers. Fuzzy \(\alpha , \beta \)-cuts are respectively used in the objective functions and constraints to equivalently transform the bi-level fuzzy optimization into bi-level interval valued form. Subsequently, a bi-level bi-objective linear fractional programming problem is generated. Change of variable method is implemented to construct linear fuzzy membership functions at upper and lower level. Fuzzy goal programming eliminating over deviations from aspiration level of fuzzy membership functions along with a proposed modified linearization process of fractional functions are together used to determine the compromise solution of the problem. To illustrate and justify the feasibility of the proposed method, an existing numerical problem is solved and the results obtained are comparatively analyzed.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution
Springer+ Basic
EUR 32.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or Ebook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now
Chapter
EUR 29.95
Price includes VAT (Germany)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
eBook
EUR 245.03
Price includes VAT (Germany)
  • Available as EPUB and PDF
  • Read on any device
  • Instant download
  • Own it forever
Softcover Book
EUR 320.99
Price includes VAT (Germany)
  • Compact, lightweight edition
  • Dispatched in 3 to 5 business days
  • Free ship** worldwide - see info
Hardcover Book
EUR 320.99
Price includes VAT (Germany)
  • Durable hardcover edition
  • Dispatched in 3 to 5 business days
  • Free ship** worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Similar content being viewed by others

References

  1. Abo-Sinna MA (2001) A bi-level non-linear multi-objective decision making under fuzziness. Opsearch 38(5):484–495

    Article  MathSciNet  MATH  Google Scholar 

  2. Arora SR, Gupta R (2009) Interactive fuzzy goal programming approach for bilevel programming problem. Eur J Oper Res 194(2):368–376

    Article  MathSciNet  MATH  Google Scholar 

  3. Arya R, Singh P, Kumari S, Obaidat MS (2020) An approach for solving fully fuzzy multi-objective linear fractional optimization problems. Soft Computing 24(12):9105–9119

    Article  MATH  Google Scholar 

  4. Borza M, Rambely AS (2022) An approach based on \( alpha \)-cuts and max-min technique to linear fractional programming with fuzzy coefficients. Iran J Fuzzy Syst 19(1):153–168

    MathSciNet  MATH  Google Scholar 

  5. Calvete HI, Galé C (1999) The bilevel linear/linear fractional programming problem. Eur J Oper Res 114(1):188–197

    Article  MATH  Google Scholar 

  6. Chakraborty M, Gupta S (2002) Fuzzy mathematical programming for multi objective linear fractional programming problem. Fuzzy Sets Syst 125(3):335–342

    Article  MathSciNet  MATH  Google Scholar 

  7. Charnes A, Cooper WW (1962) Programming with linear fractional functionals. Naval Res Logistics Q 9(3–4):181–186

    Article  MathSciNet  MATH  Google Scholar 

  8. Toksari MD (2010) Taylor series approach for bi-level linear fractional programming problem. Selçuk J Appl Math 11(1):63–69

    MathSciNet  MATH  Google Scholar 

  9. Hirche J, Craven BD (1989) Fractional programming. Berlin, Heldermann Verlag 1988, 145 p, DM 48. ISBN 3-88538-404-3 (Sigma Series in Applied Mathematics 4). Zeitschrift Angewandte Mathematik und Mechanik, 69(10), 371–371 (1989)

    Google Scholar 

  10. Malhotra N, Arora SR (2000) An algorithm to solve linear fractional bilevel programming problem via goal programming. Opsearch 37(1):1–13

    Article  MathSciNet  MATH  Google Scholar 

  11. Mehra A, Chandra S, Bector CR (2011) Acceptable optimality in linear fractional programming with fuzzy coefficients. Fuzzy Optim Decis Making 6(1):5–16

    Article  MathSciNet  MATH  Google Scholar 

  12. Miettinen K (2012) Nonlinear multiobjective optimization (Vol 12). Springer Science & Business Media

    Google Scholar 

  13. Mishra S (2007) Weighting method for bi-level linear fractional programming problems. Eur J Oper Res 183(1):296–302

    Article  MATH  Google Scholar 

  14. Pal BB, Moitra BN, Maulik U (2003) A goal programming procedure for fuzzy multiobjective linear fractional programming problem. Fuzzy Sets Syst 139(2):395–405

    Article  MathSciNet  MATH  Google Scholar 

  15. Pramanik S, Dey PP (2011) Bi-level linear fractional programming problem based on fuzzy goal programming approach. Int J Comput Appl 25(11):34–40

    Google Scholar 

  16. Saad OM, Hafez MS (2011) An algorithm for solving bi-level integer linear fractional programming problem based on fuzzy approach. General Math Notes 3:86–99

    Google Scholar 

  17. Stancu-Minasian IM (2012) Fractional programming: theory, methods and applications (Vol 409). Springer Science & Business Media

    Google Scholar 

  18. Stanojević B, Dzitac S, Dzitac I (2020) Fuzzy numbers and fractional programming in making decisions. Int J Inf Technol Decis Making 19(04):1123–1147

    Article  Google Scholar 

  19. Thirwani D, Arora SR (1993) Bi-level linear fractional programming problem. Cahiers du Centre d’études de recherche opérationnelle 35(1–2):135–149

    MathSciNet  MATH  Google Scholar 

  20. Veeramani C, Sumathi M (2016) A new method for solving fuzzy linear fractional programming problems. J Intell Fuzzy Syst 31(3):1831–1843

    Article  MATH  Google Scholar 

  21. Zimmermann HJ (2011) Fuzzy set theory and its applications. Springer Science & Business Media

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, School of Applied Sciences, KIIT Deemed to be University, Bhubaneswar, 751024, Odisha, India

    Sujit Maharana & Suvasis Nayak

Authors
  1. Sujit Maharana
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Suvasis Nayak
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Suvasis Nayak .

Editor information

Editors and Affiliations

  1. Department of Computer Science and Engineering, Jahangirnagar University, Dhaka, Bangladesh

    Mohammad Shorif Uddin

  2. Department of Mathematics, South Asian University, New Delhi, India

    Jagdish Chand Bansal

Rights and permissions

Reprints and permissions

Copyright information

© 2023 The Author(s), under exclusive license to Springer Nature Singapore Pte Ltd.

About this paper

Check for updates. Verify currency and authenticity via CrossMark

Cite this paper

Maharana, S., Nayak, S. (2023). Bi-Level Linear Fuzzy Fractional Programming Problem Under Trapezoidal Fuzzy Environment: A Solution Approach. In: Uddin, M.S., Bansal, J.C. (eds) Proceedings of International Joint Conference on Advances in Computational Intelligence. IJCACI 2022. Algorithms for Intelligent Systems. Springer, Singapore. https://doi.org/10.1007/978-981-99-1435-7_38

Download citation

Publish with us

Policies and ethics

Search

Navigation