Neutronics of Lead and Bismuth

Abstract

Cross-section uncertainties of Pb and Bi isotopes could consequently affect the precision of nuclear design calculations of preliminary analyses, before the actual operation of upcoming ADS, since Pb and Bi are composed partly of coolant material (lead-bismuth eutectic: LBE) in ADS facilities. The main characteristics of LBE in ADS are recognized as follows: chemically inactive; high boiling point mechanically; excellent neutron economy caused by large scattering cross sections. From the viewpoint of neutronics, LBE exerts considerable impact on nuclear design parameters for numerical simulations of neutron interactions of Pb and Bi isotopes. As a suitable way of investigating cross-section uncertainties, sample reactivity worth measurements in critical states are considered effective with the use of reference and test materials in a zero-power state, such as a critical assembly, because integral parameter information on cross sections of test materials can be acquired experimentally. For the required experimental study on Pb and Bi nuclear data uncertainties, the sample reactivity worth experiments are carried out at the KUCA core by the substitution of reference (aluminum) for test (Pb or Bi) materials, and numerical simulations are performed with stochastic and deterministic calculation codes together with major nuclear data libraries.

7.1 Sample Reactivity Worth Experiments

7.1.1 Core Configuration

7.1.1.1 Lead Sample Reactivity Worth

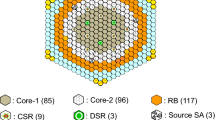
The lead (Pb) sample reactivity experiments [1, 2] were carried out in the A-core (Fig. 7.1) that has polyethylene moderator (polyethylene “p” in Fig. 7.1) and reflector (conventional polyethylene) rods, and four different fuel assemblies: normal “F,” partials “40” and “14,” and reference “f” fuel assemblies (Figs. 7.2a–d, respectively). Normal fuel assembly “F” is composed of 60 unit cells, and upper and lower polyethylene blocks about 24″ and 21″ long, respectively, in an aluminum (Al) sheath. For the normal and partial fuel assemblies, a unit cell in the fuel region is composed of a highly enriched uranium (HEU) fuel plate 1/16″ thick and polyethylene plate 1/8″ thick. The numerals 40 and 14 correspond to the number of fuel plates in the partial fuel assembly used for reaching the criticality mass. The reference fuel assembly “f” is composed of 40 unit cells with an HEU fuel plate 1/16″ thick and Al plate 1/16″ thick, 20 unit cells of HEU and the polyethylene plate as in the normal fuel assembly, as shown in Fig. 7.2d.

Fig. 7.1

Top view of the KUCA A-core in sample reactivity experiments (Reference core) (Ref. [1])

Fig. 7.2

Schematic drawing of fuel assemblies in the KUCA A-core (Fig. 7.1) (Ref. [1])

7.1.1.2 Bismuth Sample Reactivity Worth

The bismuth (Bi) sample reactivity worth experiments [3] were carried out in the A-core (Fig. 7.3), which has polyethylene moderator and reflector rods, and four different fuel assemblies, including HEU, polyethylene moderator (p), polyethylene reflector (PE), graphite (Gr) and Al plate: normal “F,” partials “40” and “14” and test “f” (Figs. 7.4a–d, respectively).

Fig. 7.3

Top view of the KUCA A-core in Bi sample reactivity worth experiments (Reference core) (Ref. [3])

Fig. 7.4

Schematic drawing of fuel assemblies (Fig. 7.3) in the A-core (Ref. [3])

7.1.2 Experimental Settings

In the sample reactivity experiments, a test-zoned fuel region was arranged for measuring the effects of substituting Al plates for Pb or Bi ones upon the criticality. In the test zone, five test fuel assemblies were set around the core at positions (14, M), (15, L), (15, M), (15, O) and (16, M), as shown in Figs. 7.1 and 7.3. The patterns of sample reactivity experiments were ranging between three and five, as shown in Fig. 7.5, substituting the reference fuel rods for Pb or Bi fuel rods. The test fuel rod was the same as in the reference fuel rod substituting Al plates for Pb or Bi ones shown in Fig. 7.6. The spectrum of experimental core at KUCA was compared with that of LBE core [4] in the JAEA ADS model, as shown in Fig. 7.7. The experimental core was a relatively hard spectrum one implemented in KUCA, though not to a fast spectrum core in actual ADS. The substitution was conducted in a total of 40 unit cells of the central region of fuel rods, such as changing Al plates in Figs. 7.2d and 7.4d into Pb and Bi ones in Figs. 7.6a, b, respectively. The sample reactivity caused by the substitution was experimentally obtained through the difference between the excess reactivities of Al reference core and Pb or Bi test core. In the experiments, the critical state was adjusted by maintaining the control rods (C1, C2 and C3) in certain positions shown in Tables 7.1 and 7.2; the excess reactivity was then deduced by the difference between the critical and super-critical states in the core. The experimental excess reactivity was obtained with the combined use of both the reactivity worth of each control rod evaluated by the rod drop method and its integral calibration curve obtained by the positive period method.

Fig. 7.5

Patterns of sample reactivity worth experiments (Refs. [1,2,3])

Fig. 7.6

Schematic drawing of test fuel rods

Fig. 7.7

Comparison between the neutron spectra of HEU-Pb test zone in KUCA and LBE-cooled core in JAEA ADS model (Ref. [1])

Table 7.1 Control rod positions at critical state in Al reference and Pb test cores (Cases 1 through 4) (Ref. [1])

Table 7.2 Control rod positions at critical state in Al reference and Bi test cores (Cases 1 through 4) (Ref. [3])

The estimated experimental error of excess reactivity measurement was less than 5%. In the Al reference and Pb or Bi test cores, the effective delayed neutron fraction (β_eff) was acquired by MCNP6.1 [5] (2,000 active cycles of 50,000 histories; 2 pcm statistical error) with JENDL-4.0, [6] and the values of 798 and 801 pcm were applied to these two cores, respectively, when the excess reactivity in dollar units was converted into that in pcm units.

7.2 Monte Carlo Analyses

7.2.1 Evaluation Method

Experimental sample reactivity worth $\Delta \rho_{{{\text{Al}} \to {\text{Pb}}}}^{\text{Exp}}$ was deduced by the difference between two excess reactivities $\Delta \rho_{\text{Excess}}^{\text{Exp,Al}}$ and $\Delta \rho_{\text{Excess}}^{\text{Exp,Pb}}$ obtained by the positive period method in the reference and test cores, respectively, as follows, when the Al plates were substituted for the Pb (or Bi) ones:

$$\begin{aligned} \Delta \rho_{{{\text{Al}} \to {\text{Pb}}}}^{\text{Exp}} = & \rho_{\text{Excess}}^{\text{Exp,Pb}} - \rho_{\text{Excess}}^{\text{Exp,Al}} = \left( {1 - \frac{1}{{k_{\text{Clean}}^{\text{Exp,Pb}} }}} \right) - \left( {1 - \frac{1}{{k_{\text{Clean}}^{\text{Exp,Al}} }}} \right) \\ = & \frac{1}{{k_{\text{Clean}}^{\text{Exp,Al}} }} - \frac{1}{{k_{\text{Clean}}^{\text{Exp,Pb}} }}, \\ \end{aligned}$$

(7.1)

where $k_{\text{Clean}}^{\text{Exp,Al}}$ and $k_{\text{Clean}}^{\text{Exp,Pb}}$ indicate the effective multiplication factors deduced by the experimental excess reactivities obtained in super-critical cores (clean core) before (Al) and after (Pb or Bi) substituting Al plates for Pb ones, respectively, under the condition of all the control and safety rods withdrawn.

In the MCNP analyses, numerical sample reactivity worth $\Delta \rho_{{{\text{Al}} \to {\text{Pb}}}}^{\text{MCNP}}$ was deduced by the difference between two excess reactivities $\Delta \rho_{\text{Excess}}^{\text{MCNP,Al}}$ and $\Delta \rho_{\text{Excess}}^{{{\text{MCNP,}}\,{\text{Pb}}}}$ in the reference and test cores, respectively, as follows, with the same method as that of experimental sample reactivity:

$$\begin{aligned} \Delta \rho_{{{\text{Al}} \to {\text{Pb}}}}^{\text{MCNP}} = & \rho_{\text{Excess}}^{\text{MCNP,Pb}} - \rho_{\text{Excess}}^{\text{MCNP,Al}} = \left( {\frac{1}{{k_{\text{Critical}}^{\text{MCNP,Pb}} }} - \frac{1}{{k_{\text{Clean}}^{\text{MCNP,Pb}} }}} \right) \\ - & \left( {\frac{1}{{k_{\text{Critical}}^{\text{MCNP,Al}} }} - \frac{1}{{k_{\text{Clean}}^{\text{MCNP,Al}} }}} \right), \\ \end{aligned}$$

(7.2)

where $k_{\text{Clean}}^{\text{MCNP,Al}}$ and $k_{\text{Clean}}^{\text{MCNP,Pb}}$ indicate the effective multiplication factors in super-critical cores before and after substituting Al plates for Pb ones, respectively. Also, $k_{\text{Critical}}^{\text{MCNP,Al}}$ and $k_{\text{Critical}}^{\text{MCNP,Pb}}$ need to be defined as the values of the effective multiplication factors in critical cores before and after substituting Al plates for Pb ones, since these numerical values always are not unity.

On the basis of the experimental methodology shown in Eq. (7.1), the numerical approach of sample reactivity worth $\Delta \rho_{{{\text{Al}} \to {\text{Pb}}}}^{\text{Cal}}$ can be generally expressed as follows, in case of substituting Al plates for Pb ones:

$$\begin{aligned} \Delta \rho_{{{\text{Al}} \to {\text{Pb}}}}^{\text{Cal}} \, = & \rho_{\text{Excess}}^{\text{Cal,Pb}} - \rho_{\text{Excess}}^{\text{Cal,Al}} = \left( {1 - \frac{1}{{k_{\text{Clean}}^{\text{Cal,Pb}} }}} \right) - \left( {1 - \frac{1}{{k_{\text{Clean}}^{\text{Cal,Al}} }}} \right) \\ = & \frac{1}{{k_{\text{Clean}}^{\text{Cal,Al}} }} - \frac{1}{{k_{\text{Clean}}^{{{\text{Cal,}}\,{\text{b}}}} }}, \\ \end{aligned}$$

(7.3)

where $k_{\text{Clean}}^{\text{Cal,Al}}$ and $k_{\text{Clean}}^{\text{Cal,Pb}}$ indicate the effective multiplication factors in super-critical cores.

Numerical sample reactivity $\Delta \rho_{{{\text{Al}} \to {\text{Pb}}}}^{\text{MCNP}}$ in Eq. (7.2) can be rewritten with the use of the concept of Eq. (7.3), as follows:

$$\begin{aligned} \Delta \rho_{{{\text{Al}} \to {\text{Pb}}}}^{\text{MCNP}} = & \rho_{\text{Excess}}^{\text{MCNP,Pb}} - \rho_{\text{Excess}}^{\text{MCNP,Al}} = \left( {\frac{1}{{k_{\text{Critical}}^{\text{MCNP,Pb}} }} - \frac{1}{{k_{\text{Clean}}^{\text{MCNP,Pb}} }}} \right) \\ - & \left( {\frac{1}{{k_{\text{Critical}}^{\text{MCNP,Al}} }} - \frac{1}{{k_{\text{Clean}}^{\text{MCNP,Al}} }}} \right) \\ = & \Delta_{{{\text{Critical,}}\,{\text{Al}} \to {\text{Pb}}}}^{\text{MCNP}} + \left( {\frac{1}{{k_{\text{Clean}}^{\text{MCNP,Al}} }} - \frac{1}{{k_{\text{Clean}}^{\text{MCNP,Pb}} }}} \right), \\ \end{aligned}$$

(7.4)

where $\Delta_{{{\text{Critical,Al}} \to {\text{Pb}}}}^{\text{MCNP}}$ indicates the difference between inverse values of eigenvalue calculations in the two critical states evaluated by MCNP6.1. Here, the first term in Eq. (7.4) is defined as “criticality bias” as follows:

$$\Delta_{{{\text{Critical,Al}} \to {\text{Pb}}}}^{\text{MCNP}} = \frac{1}{{k_{\text{Critical}}^{\text{MCNP,Al}} }} - \frac{1}{{k_{\text{Critical}}^{\text{MCNP,Pb}} }}.$$

(7.5)

By introducing the evaluation methodology of the numerical sample reactivity worth shown in Eq. (7.3), $\Delta_{{{\text{Clean,J}}40\, \to \,{\text{xxx,}}\,{\text{yy}} - {\text{zzz}}}}^{{{\text{MCNP,Al}} \to {\text{Pb}}}}$ is investigated on the numerical sample reactivity worth as follows, when the nuclear data libraries and isotopes are varied in the MCNP calculations:

$$\begin{aligned} \Delta_{{{\text{Clean,J}}40 \to {\text{xxx,}}\,{\text{yy}} - {\text{zzz}}}}^{{{\text{MCNP,Al}} \to {\text{Pb}}}} = & \left( {\frac{1}{{k_{\text{Clean,J40,All}}^{\text{MCNP,Al}} }} - \frac{1}{{k_{\text{Clean,J40,All}}^{\text{MCNP,Pb}} }}} \right) \\ - & \left( {\frac{1}{{k_{{{\text{Clean,xxx,}}\,{\text{yy}} - {\text{zzz}}}}^{\text{MCNP,Al}} }} - \frac{1}{{k_{{{\text{Clean,xxx,}}\,{\text{yy}} - {\text{zzz}}}}^{\text{MCNP,Pb}} }}} \right), \\ \end{aligned}$$

(7.6)

where J40 indicates the JENDL-4.0 library, All all the related isotopes and xxx a suitable choice of three nuclear data libraries: JENDL-3.3 [7], ENDF/B-VII.0 [8] and JEFF-3.1 [9], yy an isotope and zzz a mass of isotopes.

7.2.2 Lead Sample Reactivity Worth

7.2.2.1 Numerical Simulations

The numerical analyses were conducted with the use of MCNP6.1 together with the JENDL-3.3, JENDL-4.0, ENDF/B-VII.0 and JEFF-3.1 for transport. For actual experimental analyses, the capability of eigenvalue calculations by MCNP6.1 was useful to be discussed with the use of JENDL-4.0 in processing important data analyses. Also, JENDL-4.0, as a reference library, was compared with the other nuclear data libraries to reveal its uncertainty.

In the reference core shown in Fig. 7.1, criticality was reached by adjusting the position of control rod C2 and withdrawing control rods C1 and C3, and safety rods S4, S5 and S6 from the core, and excess reactivity was deduced with the combined use of control rod worth (C2) by the rod drop method and its calibration curve by the positive period method. The measured excess reactivity was within an uncertainty of 5%, and compared with the numerical one as shown in Table 7.3. The numerical excess reactivity was obtained by the MCNP6.1 eigenvalue calculations with JENDL-4.0 within a statistical error of 2 pcm through 2,000 active cycles of 25,000 histories and estimated with the use of the two eigenvalue calculations in critical and super-critical states. From a comparison between measured and calculated results shown in Table 7.3, the C/E (calculation/experiment) value revealed good agreement with a relative difference of 7%.

Table 7.3 Comparison between the results of measured and calculated excess reactivities in reference core shown in Fig. 7.1 (Ref. [1])

Furthermore, in the reference core, the measured control rod worth was compared with the calculated one, using the same method as for the excess reactivity. The results are as shown in Table 7.4. The MCNP eigenvalue calculations reproduced the experimental results of control rod worth accurately, with the C/E values within 2%, ranging between 350 and 1,000 pcm, regardless of the kind of control rod used (Table 7.4).

Table 7.4 Comparison between the results of measured and calculated control rod worth in reference core shown in Fig. 7.1 (Ref. [1])

7.2.2.2 Eigenvalue Bias

On the basis of Eq. (7.2), numerical analyses of sample reactivity were conducted by the MCNP6.1 eigenvalue calculations with nuclear data libraries as in Sect. 7.2.2.1. In numerical simulations, sample reactivity worth was obtained by the two eigenvalue calculations in both critical and super-critical states: the difference between the inverse values of eigenvalue calculations in the two states. The calculated results of the sample reactivity were obtained by varying the nuclear data libraries, as shown in Table 7.5 (comparison between Eqs. (7.1) and (7.2)), and, through an estimation of C/E values, were compared at a high accuracy with the experimental results in almost all cases, regardless of the kind of nuclear data libraries used. From the calculated results in Tables 7.3 through 7.5, the precision of MCNP6.1 with JENDL-4.0 was considered fairly good in the eigenvalue calculations, and JENDL-4.0 was found reliable as a reference nuclear data library, comparing it with JENDL-3.3.

Table 7.5 Comparison between the results of measured and calculated sample reactivities evaluated by Eqs. (7.1) and (7.2), respectively, by substituting Al plates for Pb ones as shown in Fig. 7.5 (Ref. [1])

Prior to the MCNP numerical analyses, in the experiment results, interesting discussions were provided from two aspects. First, the positive reactivity effect was found in the sample reactivity experiments substituting Al plates for Pb ones, and was mainly attributable to the difference between the values of moderating ratio (ξΣ_s/Σ_a: ξ, Σ_s and Σ_a indicate the average logarithmic energy decrement, macro cross sections of scattering and absorption, respectively.) in Al and Pb. Second, while the number of substitution of fuel rods was the same as in both Cases 1 and 2, a significant difference between sample reactivities was involved in the forward and adjoint functions of reactivity defined in the First-order perturbation theory with the variation of core sizes in horizontal and vertical directions shown in Fig. 7.1.

7.2.2.3 Criticality Bias

As discussed in Sect. 7.2, the ability of MCNP6.1 calculations was confirmed in terms of the general definition of sample reactivity by the MCNP approach. Here, the main objective of this study was to compare the experimental and numerical sample reactivities defined in Eqs. (7.1) and (7.3), respectively. By comparing Eqs. (7.1) and (7.3), as shown in Table 7.6, considering the uncertainties of C/E values, the accuracy of the numerical analyses by MCNP6.1 with JENDL-4.0 demonstrated a relative difference of about 5% and an overestimation by more than 50% with JENDL-3.3. By comparing JENDL-3.3 and JENDL-4.0, the calculated values with JENDL-4.0 improved more with a high accuracy of 30% in the C/E values than with the values calculated with JENDL-3.3. Regarding libraries ENDF/B-VII.0 and JEFF-3.1, the calculated sample reactivities were considered well within the relative difference of 10% as shown in Table 7.6.

Table 7.6 Comparison between the results of measured and calculated sample reactivities evaluated by Eqs. (7.1) and (7.3), respectively, by substituting Al plates for Pb ones as shown in Fig. 7.5 (Ref. [1])

Mention should be made, however, of the accuracy of the numerical analyses obtained by MCNP with the four libraries, especially the absolute values by JENDL-4.0, as shown in Table 7.6. Further investigation was needed to find the reason for the discrepancy of unit C/E values with JENDL-4.0. Consequently, in addition to the concept of eigenvalue bias mentioned in Sect. 7.2.2.2, a different evaluation, here termed “criticality bias,” of sample reactivity worth was introduced to investigate C/E discrepancy, when the formulation of sample reactivity by MCNP6.1 defined in Eq. (7.2) is changed to that in Eq. (7.4). As shown in Eq. (7.5), the criticality bias $\Delta_{{{\text{Critical,}}\,{\text{Al}} \to {\text{Pb}}}}^{\text{MCNP}}$ by the MCNP approach was obtained by the difference between reactivity-like criticalities in critical cores by substituting of Al plates for Pb ones, and interpreted as a bias of reactivity induced by the difference between the experiments and the eigenvalue calculations. By the introduction of criticality bias in Eq. (7.5), a small discrepancy in C/E values (Table 7.6) was found in the numerical simulations.

On the basis of Eq. (7.5), criticality bias $\Delta_{{{\text{Critical,}}\,{\text{Al}} \to {\text{Pb}}}}^{\text{MCNP}}$ was compared with each nuclear data library as shown in Fig. 7.8 and Table 7.7. JENDL-4.0 revealed the bias around 20 pcm; JENDL-3.3 a further bias ranging between 50 and 100 pcm; ENDF/B-VII.0 a relatively small bias less than 20 pcm, compared with the JENDL libraries. Among the four libraries, JEFF-3.1 compared favorably with a small bias around 10 pcm, and resulted in a markedly high accuracy of C/E values, as shown in Table 7.6.

Fig. 7.8

Comparison between the values of criticality bias in critical states evaluated by Eq. (7.4) (Ref. [1])

Table 7.7 Comparison between the results of criticality bias by four nuclear data libraries corresponding to Fig. 7.8 (Ref. [1])

7.2.2.4 Discussion

Special attention was paid to the second term in Eq. (7.4) to investigate the difference between JENDL libraries mentioned in Sect. 7.2.2.3. The second term in Eq. (7.4) was significantly demonstrated in actual sample reactivity by the MCNP analyses, as well as by the experiments, and the bias between JENDL-4.0 and the other libraries were studied with a new definition, as shown in Eq. (7.6): contribution of individual isotope to sample reactivity. In the analyses of differences defined in Eq. (7.6), JENDL-4.0 was selected as the reference library, and the sample reactivities in clean cores were obtained, as shown in Figs. 7.9a, d along with four cases in Fig. 7.5, respectively, when the libraries and isotopes were varied separately: core composition materials of Pb isotopes, ²⁷Al, ²³⁵U and ²³⁸U in the fuel rod of the core.

Fig. 7.9

Comparison between the values of difference in Eq. (7.6) in JENDL-4.0 and other nuclear data libraries (Ref. [1])

A comparison between the two JENDL libraries showed a significant effect on the reactivity resulting from large differences among all Pb isotopes (²⁰⁴Pb, ²⁰⁶Pb, ²⁰⁷Pb and ²⁰⁸Pb), regardless of the magnitude of sample reactivity: especially from those of ²⁰⁶Pb and ²⁰⁷Pb; contrary to that among the others (²⁷Al, ²³⁵U and ²³⁸U). Regarding the discussion between the two JENDL libraries, the reason for total difference was attributable mainly to those of all Pb isotopes through the analyses of differences in Eq. (7.6). As discussed in previous studies [11, 12], this fact provided valuable knowledge that an improvement of the inelastic scattering cross sections around a few MeV neutron energy region of ²⁰⁶Pb and ²⁰⁷Pb had been pointed out importantly in the difference between JENDL-3.3 and JENDL-4.0 libraries through the analyses of the Pb void reactivity in the JAEA ADS model [10] and of the Pb reflector effect on SEG experiments through JENDL-4.0 benchmarks [12]. From the results of ENDF/B-VII.0, a small effect of the difference was compared inversely with that in JENDL-4.0 about 20 pcm in all cases, with regard to Pb isotopes and ²⁷Al, but not to ²³⁵U and ²³⁸U, although the total difference between JENDL-4.0 and ENDF/B-VII.0 was slight.

Furthermore, while a difference about 20 pcm was found in ²³⁸U and ²⁷Al of Cases 2 and 4, respectively, the difference between JENDL-4.0 and JEFF-3.1 was considered notably minor within the allowance of relative errors.

On the basis of these observations, a library update from JENDL-3.3 to JENDL-4.0 was demonstrated by the fact that the difference between Pb isotopes of the two JENDL libraries was dominant in the comparative study, through the numerical analyses of sample reactivity by the MCNP approach. Moreover, JENDL-4.0 revealed a slight difference from ENDF/B-VII.0 in all the Pb isotopes to ²⁷ Al, and from JEFF-3.1 in ²³⁸U to ²⁷Al.

7.2.3 Bismuth Sample Reactivity Worth

7.2.3.1 Eigenvalue Calculations

Numerical analyses were conducted with the use of the Monte Carlo code MCNP6.1 together with the JENDL-4.0 nuclear data library for transport. For actual experimental analyses, the capability of eigenvalue calculations by MCNP6.1 was useful in the discussion with the use of JENDL-4.0 for processing important data analyses, and JENDL-4.0 has already been compared with other nuclear data libraries in a previous study [4], while demonstrating a reference library.

In the reference core shown in Fig. 7.3, criticality was reached by adjusting the position of control rod C2 and withdrawing control rods C1 and C3, and safety rods S4, S5 and S6 from the core; excess reactivity was then deduced from the combined use of control rod worth of C2 by the rod drop method and its calibration curve by the positive period method. The measured excess reactivity was attained within an uncertainty of 3%, and compared with the numerical one as shown in Table 7.8. Here, effective delayed neutron fraction (β_eff) was attained by MCNP6.1 with JENDL-4.0 in both reference (Al: 798 ± 3 pcm) and test (Bi: 801 ± 3 pcm) cores. Since two values were almost same within statistical errors, the β_eff in reference core was used, when converting measured values in dollar units into ones in pcm units. The numerical excess reactivity was obtained by the MCNP6.1 eigenvalue calculations with JENDL-4.0 within a statistical error of 6 pcm through 2,000 active cycles of 25,000 histories. By comparing the measured and calculated results shown in Table 7.8, the C/E (calculation/experiment) value revealed good agreement within a relative difference of 4%, except in Case 1.

Table 7.8 Comparison between the results of measured and calculated (Eq. (7.2); MCNP6.1) excess reactivities in reference (Al) and test (Bi) cores (Ref. [3])

Furthermore, the measured control rod worth in the reference core was compared with the calculated one by the same method used for excess reactivity, as shown in Table 7.9. As shown in Tables 7.8 and 7.9, the MCNP eigenvalue calculations with JENDL-4.0 revealed accurate reproduction of the experimental results of excess reactivity and control rod worth, respectively, with the C/E values within 6%, ranging widely between 87 and 945 pcm.

Table 7.9 Comparison between the results of measured and calculated (MCNP6.1) control rod worth in reference core (Al reference core) (Ref. [3])

7.2.3.2 Criticality Bias

As discussed in Sect. 7.2.3.1, the accuracy of MCNP6.1 calculations was confirmed in terms of the general definition of sample reactivity worth by the MCNP approach. Here, the actual objective of this subsection was to compare the difference between experimental and numerical sample reactivity worth defined in Eqs. (7.1) and (7.2), respectively, and to confirm the precision of MCNP calculations of the Bi sample reactivity worth experiments.

Special mention is made of the accuracy of numerical results by MCNP, especially of the absolute values shown in Table 7.10, and additional investigation was requisite to find the reason for the discrepancy between the results of experiments and calculations in Eq. (7.4) shown in Table 7.10. Then, as suggested in Sect. 7.2.1, “criticality bias” of sample reactivity worth was useful in the investigation of the discrepancy, when a formulation of sample reactivity worth by MCNP6.1 defined in Eq. (7.2) is changed into that by Eq. (7.4). The criticality bias $\Delta_{{{\text{Critical,Al}} \to {\text{Bi}}}}^{\text{MCNP}}$ defined in Eq. (7.5) was around 30 pcm, as shown in Table 7.10 and Fig. 7.10. From these results, the criticality bias of 37 pcm at most was confirmed as being included in the sample reactivity worth about 80 pcm, even in the analyses of MCNP calculations, although the absolute value of sample reactivity worth was small.

Table 7.10 Comparison of measured and calculated Bi sample reactivity worth in Eqs. (7.1) and (7.4), respectively, and criticality bias in Eq. (7.5) (Ref. [3])

Fig. 7.10

Comparison between the values of criticality bias at critical state evaluated by Eq. (7.5) (Ref. [3])

7.3 Sensitivity Coefficients

7.3.1 Theoretical Background

7.3.1.1 Sensitivity Coefficients

The sensitivity coefficient S of the integral reactor physics parameter R is defined by the ratio of the rate of change in R and a certain parameter x as follows:

$$S\, = \,{{\frac{dR}{R}} \mathord{\left/ {\vphantom {{\frac{dR}{R}} {\frac{dx}{x}}}} \right. \kern-0pt} {\frac{dx}{x}}}.$$

(7.7)

The effective multiplication factor k_eff can be expressed by a balance equation of neutrons as follows:

$${\mathbf{A}}\phi \, = \,\frac{1}{{k_{\text{eff}} }}{\mathbf{F}}\phi ,$$

(7.8)

where A and F indicate operators of transport and fission terms, respectively, and ϕ the forward neutron flux. Multiplying Eq. (7.8) by adjoint neutron flux ϕ^* and integrating over whole volume and energy, the following equation is obtained:

$$\frac{1}{{k_{\text{eff}} }}\, = \,\frac{{\left\langle {\phi^{*} {\mathbf{A}}\phi } \right\rangle }}{{\left\langle {\phi^{*} {\mathbf{F}}\phi } \right\rangle }},$$

(7.9)

where brackets <> indicate an integration over the whole volume and energy.

Assuming that the value of k_eff is a function x, taking the logs of both sides in Eq. (7.9) and differentiating Eq. (7.9) with respect to x, the following equation is obtained, on the basis of theoretical considerations [13,14,15,16]:

$$\begin{aligned} - & \frac{d}{dx}\log k_{\text{eff}} \, = \,\frac{d}{dx}\log \left( {\left\langle {\phi^{*} {\mathbf{A}}\phi } \right\rangle } \right) - \frac{d}{dx}\log \left( {\left\langle {\phi^{*} {\mathbf{F}}\phi } \right\rangle } \right) \\ \Leftrightarrow - & \frac{1}{{k_{\text{eff}} }}\frac{d}{dx}k_{\text{eff}} = \frac{1}{{\left\langle {\phi^{*} \,{\mathbf{A}}\,\phi } \right\rangle }}\frac{d}{dx}\left\langle {\phi^{*} {\mathbf{A}}\phi } \right\rangle - \frac{1}{{\left\langle {\phi^{*} {\mathbf{F}}\phi } \right\rangle }}\frac{d}{dx}\left\langle {\phi^{*} {\mathbf{F}}\phi } \right\rangle \\ = & \frac{{\left\langle {\frac{\partial }{\partial x}\phi^{*} {\mathbf{A}}\phi } \right\rangle }}{{\left\langle {\phi^{*} {\mathbf{A}}\phi } \right\rangle }} - \frac{{\left\langle {\frac{\partial }{\partial x}\phi^{*} {\mathbf{F}}\phi } \right\rangle }}{{\left\langle {\phi^{*} {\mathbf{F}}\phi } \right\rangle }} + \frac{{\left\langle {\phi^{*} \frac{\partial }{\partial x}{\mathbf{A}}\phi } \right\rangle }}{{\left\langle {\phi^{*} {\mathbf{A}}\phi } \right\rangle }} - \frac{{\left\langle {\phi^{*} \frac{\partial }{\partial x}{\mathbf{F}}\phi } \right\rangle }}{{\left\langle {\phi^{*} {\mathbf{F}}\phi } \right\rangle }} \\ + & \frac{{\left\langle {\phi^{*} {\mathbf{A}}\frac{\partial }{\partial x}\phi } \right\rangle }}{{\left\langle {\phi^{*} {\mathbf{A}}\phi } \right\rangle }} - \frac{{\left\langle {\phi^{*} {\mathbf{F}}\frac{\partial }{\partial x}\phi } \right\rangle }}{{\left\langle {\phi^{*} {\mathbf{F}}\phi } \right\rangle }}. \\ \end{aligned}$$

(7.10)

With the use of an operator B, Eq. (7.8) can be expressed as follows:

$$\left( {{\mathbf{A}} - \frac{1}{{k_{{e{\text{ff}}}} }}{\mathbf{F}}} \right)\,\phi = {\mathbf{B}}\phi = 0.$$

(7.11)

Here, assuming that parameter x, operator B and neutron flux ϕ are changed into x + δx, B + δB and ϕ + δϕ, respectively, in a critical state, the following equations are obtained:

$$\left( {{\mathbf{B}} + \delta {\mathbf{B}}} \right)\left( {\phi + \delta \phi } \right) = 0.$$

(7.12)

Neglecting second-order perturbation terms, Eq. (7.11) can be expressed as follows:

$${\mathbf{B}}\delta \phi + \delta {\mathbf{B}}\phi = 0.$$

(7.13)

Introducing the generalized adjoint flux Γ^*, the following equation is obtained with the use of adjoint operator B^* and a certain adjoint source term q^*, defined as reactivity in these analyses:

$${\mathbf{B}}^{*} \varGamma^{*} = q^{*} .$$

(7.14)

Multiplying Eq. (7.13) by the generalized adjoint flux Γ ^* on the left side, and integrating over the whole volume and energy, the following equations are obtained with the use of theoretical consideration [16]:

$$\left\langle {\varGamma^{*} {\mathbf{B}}\delta \phi } \right\rangle + \left\langle {\varGamma^{*} \delta {\mathbf{B}}\phi } \right\rangle = 0,$$

(7.15)

$$q^{*} = \frac{{A^{*} \phi^{*} }}{{\left\langle {\phi^{*} A\phi } \right\rangle }} - \frac{{F^{*} \phi^{*} }}{{\left\langle {\phi^{*} F\phi } \right\rangle }}.$$

(7.16)

From the formation of q^* in Eq. (7.16), q^* is interpreted as an adjustment term for numerically obtaining Γ ^* in Eq. (7.14), on the basis of the Generalized Perturbation Method [14].

Finally, with the use of Eqs. (7.11) through (7.16), the sensitivity coefficient in Eq. (7.7) can be expressed as follows, on the basis of the first-order perturbation approximation [17]:

$$S = \frac{{\left\langle {\phi^{*} \frac{{\partial {\mathbf{A}}}}{\partial x}\phi } \right\rangle }}{{\left\langle {\phi^{*} {\mathbf{A}}\phi } \right\rangle }} - \frac{{\left\langle {\phi^{*} \frac{{\partial {\mathbf{F}}}}{\partial x}\phi } \right\rangle }}{{\left\langle {\phi^{*} {\mathbf{F}}\phi } \right\rangle }} + \left\langle {\varGamma^{*} \frac{{d{\mathbf{B}}}}{dx}\phi } \right\rangle - \left\langle {\varGamma^{*} \frac{{d{\mathbf{B}}^{*} }}{dx}\phi } \right\rangle .$$

(7.17)

7.3.1.2 Difference Between Nuclear Data Libraries

With the use of the sensitivity coefficient described in Sect. 7.3.1.1, reactivity change by a data library variation was evaluated by multiplying a relative value of cross sections between data libraries by the sensitivity coefficient.

For example, the sensitivity in JENDL-4.0 is expressed as follows:

$$S_{{\rho ,\sigma_{n,i,g}^{J40} }} = \frac{{\sigma_{n,i,g}^{J40} }}{{\rho_{J40} }} \cdot \frac{d\rho }{d\sigma },$$

(7.18)

where ρ_J40 indicates the calculated sample reactivity by JENDL-4.0, σ the microscopic cross section, n the kind of nuclides, i the kind of reactions and g the energy group. Equation (7.18) can be rewritten as follows:

$$\frac{d\rho }{{\rho_{J40} }} = \frac{d\sigma }{{\sigma_{n,i,g}^{J40} }} \cdot S_{{\rho ,\sigma_{n,i,g}^{J40} }} .$$

(7.19)

A variation $\Delta \rho_{n,i,g}^{\text{Lib}}$ of sample reactivity by some library (Lib) is evaluated by comparing with that by JENDL-4.0 as follows:

$$\Delta \rho_{n,i,g}^{\text{Lib}} = \left( {\frac{{\sigma_{n,i,g}^{\text{Lib}} - \sigma_{n,i,g}^{J40} }}{{\sigma_{n,i,g}^{J40} }} \cdot S_{{\rho ,\sigma_{n,i,g}^{J40} }} } \right) \cdot \rho_{J40} .$$

(7.20)

7.3.2 Lead Isotopes

7.3.2.1 Numerical Approach

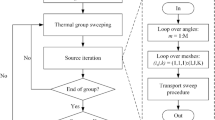
The numerical analyses were conducted with the combined use of SRAC2006 and MARBLE code systems: collision probability calculations (PIJ [18]), eigenvalue calculations (CITATION [19]), sensitivity coefficient calculations (SAGEP [20]) of SRAC2006 and uncertainty calculations (UNCERTAINTY [21]) of MARBLE shown in Fig. 7.11, coupled with JENDL-3.3, JENDL-4.0, ENDF/B-VII.0 and JEFF-3.1 nuclear data libraries. The cross-section data set in 107-energy-group processed by the NJOY code [22] is pre-installed with the use of each data library in the SRAC2006 and the MARBLE code systems, to conduct numeral analyses of the thermal neutron spectrum core, such as the KUCA core. For the experimental analyses, the accuracy of deterministic (diffusion-based) calculations by CITATION was useful in the discussion with the use of JENDL-4.0 in processing important data analyses. Also, JENDL-4.0, as a reference library in this study, was compared with other nuclear data libraries to reveal its uncertainty. Finally, covariance data of cross sections were obtained by NJOY99 with the use of cross-section data contained in JENDL-4.0.

Fig. 7.11

Calculation flow of sensitivity and uncertainty analyses (Ref. [2])

7.3.2.2 Diffusion-Based Eigenvalue Calculations

The measured excess reactivity was within an uncertainty of 5%, and compared with the numerical one as shown in Table 7.11. The numerical excess reactivity was deduced, for a clean core (all control and safety rod withdrawal) in a super-critical state, by the result of diffusion-based eigenvalue calculations (CITATION) in 107-energy-group and x-y-z dimensions (3-D) with JENDL-4.0. The numerical error was within an absolute value of about 30 pcm, compared with the experimental result, as shown in Table 7.10.

Table 7.11 Comparison between measured and calculated sample reactivities, substituting reference (Al) for test-zoned (Pb) rods in Cases 1 through 4 shown in Fig. 7.5 (Ref. [2])

Among the four cases shown in Table 7.11, CITATION reproduced the experimental results of sample reactivity with an error of about 20 pcm in Case 4, which was the maximum value in a series of Pb sample reactivity experiments. The experimental result of Case 4 was selected as a representative one in sensitivity and uncertainty analyses, because of the maximum value of experiments and an acceptable accuracy of deterministic calculations by CITATION.

7.3.2.3 Sensitivity Coefficients

Sensitivity coefficients in Eq. (7.17) of sample reactivity were analyzed by the SAGEP code, for cross-section data of inelastic scattering, elastic scattering and capture reactions in Pb isotopes (^{204, 206, 207, 208}Pb), as shown in Figs. 7.12a–c, respectively. The sensitivity coefficients of inelastic scattering reactions (Fig. 7.12a) of all Pb isotopes were found to be dominant over the high energy (MeV) region with the other two reactions. The sensitivity coefficients were relatively highly positive in ²⁰⁸Pb mostly around 1 MeV for the elastic scattering reactions (Fig. 7.12b); conversely, they were negative in all Pb isotopes for the capture reactions (Fig. 7.12c). Furthermore, as shown in Fig. 7.12c, the capture cross sections of ²⁰⁷Pb were highly sensitive in the thermal neutron region, since the neutron spectrum of the KUCA core revealed extensive thermalization ranging between 0.01 and 100 eV shown in Fig. 7.13.

Fig. 7.12

Sensitivity coefficients of sample reactivity for Pb isotopes (Ref. [2])

Fig. 7.13

Neutron spectra of HEU-PE, -Al and -Pb fuel zones in KUCA (Reg. [2])

For a comparative study of the nuclear data libraries, the contributions of reactions and energy regions were analyzed by the sample reactivity difference between JENDL-4.0 and one other nuclear library (JENDL-3.3, END/F-VII.0 or JEFF-3.1), with the use of sensitivity coefficients and variation of sample reactivity between JENDL-4.0 and another library shown in Eq. (7.20). As shown in Fig. 7.14a, the comparison between JENDL-3.3 and JENDL-4.0 was large, about 30 and 20 pcm, in inelastic scattering reactions of ²⁰⁶Pb and ²⁰⁷Pb, respectively. This tendency was taken into account for a well-known revision of inelastic scattering reactions of ^{206, 207}Pb isotope cross sections from JENDL-3.3 to JENDL-4.0. The energy breakdown of reactivity and microscopic cross sections for inelastic scattering reactions were found in the energy region ranging between 1 and 5 MeV shown in Fig. 7.14b. From the results, a large difference of sample reactivity between two JENDL libraries was attributable mainly to the contribution of inelastic scattering reactions of two ^{206, 207}Pb isotopes. Another comparison between ENDF/B-VII.0 and JENDL-4.0 revealed mainly a difference of 6 pcm in inelastic scattering reactions of ²⁰⁸Pb shown in Fig. 7.14c, and almost the same with JEFF-3.1, as well as with ENDF/B-VII.0, except for ²⁰⁸Pb isotopes, as shown in Fig. 7.14d.

Fig. 7.14

Contribution of reactivity by reactions of Pb isotopes between nuclear data libraries (Ref. [2])

7.3.3 Bismuth Isotope

Sensitivity coefficients of k_eff (Case 4) in Eq. (7.17) were analyzed by the SAGEP code, for cross-section data of inelastic scattering, elastic scattering and capture reactions in Bi isotope (²⁰⁹Bi) shown in Figs. 7.15, 7.16 and 7.17, respectively, compared as ²⁷Al, ²³⁵U and ²³⁸U that are mainly core components. The sensitivity coefficients of inelastic scattering reactions (Fig. 7.15a) of ²⁰⁹Bi were found to be dominant over the high-energy (MeV) region, like those of ²⁷Al shown in Fig. 7.15b. The sensitivity coefficients of ²⁰⁹Bi elastic scattering reactions revealed an increasing tendency between epi-thermal and fast neutron energy regions shown in Fig. 7.16a, although the coefficients of ²⁰⁹Bi and ²⁷Al were compared with the mostly same distribution around 1 MeV of the elastic scattering reactions (Figs. 7.16a, b, respectively). For the sensitivity coefficients of capture reactions, ²⁰⁹Bi was found at a highly negative peak around 10³ eV regions shown in Fig. 7.17a, whereas ²⁷Al and ²³⁵U showed a locally strong depression around the thermal neutron region, as shown in Fig. 7.17b. Nonetheless, from all the results of sensitivity coefficients, absolute values of ²⁰⁹Bi were markedly very small in vertical axes shown in Figs. 7.15, 7.16 and 7.17, as compared with the values of ²⁷Al and ²³⁵U, demonstrating that the impact of ²⁰⁹Bi cross sections was considered minor in the sensitivity coefficient analyses of k_eff in the Bi sample reactivity worth experiments at KUCA.

Fig. 7.15

Sensitivity coefficients of inelastic scattering reactions of ²⁰⁹Bi and ²⁷Al in JENDL-4.0 (Ref. [3])

Fig. 7.16

Sensitivity coefficients of elastic scattering reactions of ²⁰⁹Bi and ²⁷Al in JENDL-4.0 (Ref. [3])

Fig. 7.17

Sensitivity coefficients of capture reactions of ²⁰⁹Bi, ²⁷Al, ²³⁵U and ²³⁸U in JENDL-4.0 (Ref. [3])

7.4 Uncertainty Quantification

7.4.1 Theoretical Background

7.4.1.1 Uncertainty

As for the cross-section uncertainty analyses of nuclear data [23], the uncertainty of reactor physics parameters ν can be expressed as follows:

$$\nu \, = \,{\mathbf{G}}_{\text{tar}} \,{\mathbf{M}}\,({\mathbf{G}}_{\text{tar}} )^{{\mathbf{t}}} = \sum\limits_{i} {\sum\limits_{j} {s_{i} c_{i,\,j} s_{j} } } \equiv \sum\limits_{i} {\sum\limits_{j} {\upsilon_{i,\,j} } } (1 \le i,j \le p),$$

(7.21)

where G_tar (1 × p) indicates the sensitivity vector of reactor physics parameters, M (p × p) the covariance matrix of nuclear reaction parameters, s_i the sensitivity coefficient, c_{i, j} the covariance, υ_{i, j} the factor of uncertainty and p the number of nuclear reactions including the nuclides. Thus, the contribution of uncertainty u_i in each nuclear reaction can be defined as follows:

$$u_{i} \, \equiv \,\sum\limits_{i} {\upsilon_{i,\,j} } .$$

(7.22)

Generally, since sensitivity coefficient s_i and covariance c_{i, j} are dominant in the energy group, the factor of uncertainty is finally expressed with the use of the maximum number of energy group G as follows:

$$\upsilon_{i,\,j} \, = \,\sum\limits_{g} {\sum\limits_{g\,'} {s_{g}^{\,i} c_{g,\,g\,'}^{\,i,\,j} s_{g\,'}^{\,j} } \left( {1 \le g,g' \le G} \right)} .$$

(7.23)

7.4.1.2 Cross-Section Adjustment Method

In the cross-section adjustment method [24], probability P(T) with a certain cross-section set T is obtained as follows, assuming that a set of nuclear cross sections provides a true value in normal distribution around a true value T₀ of the nuclear cross-section set with dispersion M:

$${\text{P}}({\mathbf{T}}) = {\text{P}}({\mathbf{T}}_{{\mathbf{0}}} ) \propto \exp \,\left\{ { - \left( {{\mathbf{T}} - {\mathbf{T}}_{{\mathbf{0}}} } \right)^{t} {\mathbf{M}}^{\, - 1} \left( {{\mathbf{T}} - {\mathbf{T}}_{{\mathbf{0}}} } \right)/2} \right\}.$$

(7.24)

Substituting the values of T₀, T and M in Eq. (7.24) for those of experiments R_e, the true value of experiments R_e0 and covariance V_e of experiment errors, Eq. (7.18) can be expressed as follows:

$${\text{P}}({\mathbf{R}}_{{\mathbf{0}}} ) \propto \exp \left\{ { - \left( {{\mathbf{R}}_{{\mathbf{e}}} - {\mathbf{R}}_{{{\mathbf{e}}\,{\mathbf{0}}}} } \right)^{t} {\mathbf{V}}_{{\mathbf{e}}}^{\, - 1} \left( {{\mathbf{R}}_{{\mathbf{e}}} - {\mathbf{R}}_{{{\mathbf{e}}\,{\mathbf{0}}}} } \right)/2} \right\}.$$

(7.25)

The values R_e are distributed around true values R_e0 of experiment with covariance V_e of experimental value, giving true values T₀ of a set of nuclear cross sections. Also, the values R_c(T₀) of experiment with the true value of the nuclear data cross-section set are distributed around true value R_e0 with covariance V_e + V_m, giving true value T₀ of a set of nuclear cross sections, as follows:

$${\text{P}}({\mathbf{R}}_{{\mathbf{0}}} |{\mathbf{T}}_{{\mathbf{0}}} ) \propto \exp \left\{ { - \left( {{\mathbf{R}}_{{\mathbf{e}}} - {\mathbf{R}}_{{\mathbf{c}}} ({\mathbf{T}}_{{\mathbf{0}}} )} \right)^{t} \left( {{\mathbf{V}}_{{\mathbf{e}}} + {\mathbf{V}}_{{\mathbf{m}}} } \right)^{\, - 1} \left( {{\mathbf{R}}_{{\mathbf{e}}} - {\mathbf{R}}_{{\mathbf{c}}} ({\mathbf{T}}_{{\mathbf{0}}} )} \right)/2} \right\},$$

(7.26)

where V_m indicates the covariance of calculation value.

Using Eqs. (7.24) through (7.26), the following equations are obtained with the consideration of mathematical formulation [24]:

$$\begin{aligned} {\text{P}}({\mathbf{T}}_{{\mathbf{0}}} |{\mathbf{R}}_{{\mathbf{0}}} ) = & {\text{P}}({\mathbf{R}}_{{\mathbf{0}}} |{\mathbf{T}}_{{\mathbf{0}}} ) \cdot \frac{{{\text{P}}({\mathbf{T}}_{{\mathbf{0}}} )}}{{{\text{P}}({\mathbf{R}}_{{\mathbf{0}}} )}} \\ = & ({\text{const}} .) \cdot \exp \left[ {{{( - J)} \mathord{\left/ {\vphantom {{( - J)} {\exp \left\{ { - ({\mathbf{R}}_{{\mathbf{e}}} - {\mathbf{R}}_{{\mathbf{c}}} ({\mathbf{T}}_{{\mathbf{0}}} ))^{t} ({\mathbf{V}}_{{\mathbf{e}}} + {\mathbf{V}}_{{\mathbf{m}}} )^{ - 1} {{({\mathbf{R}}_{{\mathbf{e}}} - {\mathbf{R}}_{{\mathbf{c}}} ({\mathbf{T}}_{{\mathbf{0}}} ))} \mathord{\left/ {\vphantom {{({\mathbf{R}}_{{\mathbf{e}}} - {\mathbf{R}}_{{\mathbf{c}}} ({\mathbf{T}}_{{\mathbf{0}}} ))} 2}} \right. \kern-0pt} 2}} \right\}}}} \right. \kern-0pt} {\exp \left\{ { - ({\mathbf{R}}_{{\mathbf{e}}} - {\mathbf{R}}_{{\mathbf{c}}} ({\mathbf{T}}_{{\mathbf{0}}} ))^{t} ({\mathbf{V}}_{{\mathbf{e}}} + {\mathbf{V}}_{{\mathbf{m}}} )^{ - 1} {{({\mathbf{R}}_{{\mathbf{e}}} - {\mathbf{R}}_{{\mathbf{c}}} ({\mathbf{T}}_{{\mathbf{0}}} ))} \mathord{\left/ {\vphantom {{({\mathbf{R}}_{{\mathbf{e}}} - {\mathbf{R}}_{{\mathbf{c}}} ({\mathbf{T}}_{{\mathbf{0}}} ))} 2}} \right. \kern-0pt} 2}} \right\}}}} \right], \\ \end{aligned}$$

(7.27)

$$J{ = }\left( {{\mathbf{T}} - {\mathbf{T}}_{{\mathbf{0}}} } \right)^{t} {\mathbf{M}}^{{\, - {\mathbf{1}}}} \left( {{\mathbf{T}} - {\mathbf{T}}_{{\mathbf{0}}} } \right){ + }\left( {{\mathbf{R}}_{{\mathbf{e}}} - {\mathbf{R}}_{{\mathbf{c}}} ({\mathbf{T}}_{{\mathbf{0}}} )} \right)^{t} \left( {{\mathbf{V}}_{{\mathbf{e}}} + {\mathbf{V}}_{{\mathbf{m}}} } \right)^{\, - 1} \left( {{\mathbf{R}}_{{\mathbf{e}}} - {\mathbf{R}}_{{\mathbf{c}}} ({\mathbf{T}}_{{\mathbf{0}}} )} \right).$$

(7.28)

Introducing the sensitivity coefficient G as shown in Eq. (7.21), the relation between R_c and G is obtained as follows:

$${\mathbf{R}}_{{\mathbf{c}}} ({\mathbf{T}}_{{\mathbf{0}}} ){ = }{\mathbf{R}}_{{\mathbf{c}}} ({\mathbf{T}}) - {\mathbf{G}}\left( {{\mathbf{T}} - {\mathbf{T}}_{{\mathbf{0}}} } \right),$$

(7.29)

substituting Eq. (7.29) for Eq. (7.28) and taking the derivative of Eq. (7.28), a set of nuclear cross-sections T′ after cross-section adjustment is expressed as follows:

$${\mathbf{T'}}\;{ = }\;{\mathbf{T}} + {\mathbf{MG}}^{{\mathbf{t}}} \left( {{\mathbf{GMG}} + {\mathbf{V}}_{{\mathbf{e}}} + {\mathbf{V}}_{{\mathbf{m}}} } \right)^{\, - 1} \left( {{\mathbf{R}}_{{\mathbf{e}}} - {\mathbf{R}}_{{\mathbf{c}}} ({\mathbf{T}}_{{\mathbf{0}}} )} \right).$$

(7.30)

When the covariance of (T − T₀) in Eq. (7.29) is obtained, applying to the cross-section adjustment, the covariance M′ of T′ can be expressed as follows:

$${\mathbf{M}}\prime \,{ = }\,{\mathbf{M}}\, - \,{\mathbf{M}}\,{\mathbf{G}}^{{\mathbf{t}}} \,\left( {{\mathbf{G}}\,{\mathbf{M}}\,{\mathbf{G}} + {\mathbf{V}}_{{\mathbf{e}}} + {\mathbf{V}}_{{\mathbf{m}}} } \right)^{\, - 1} {\mathbf{GM}}.$$

(7.31)

Finally, uncertainty induced by the errors of cross sections is evaluated by the difference between GMG^t and GM′G^t before and after the cross-section adjustment, respectively.

7.4.2 Lead Isotopes

7.4.2.1 Uncertainty

The uncertainty analyses by the UNCERTAINTY code of the MARBLE system were conducted with the use of JENDL-4.0 covariance data (107-energy-group) generated by NJOY99. Since the covariance data of H, C and Al nuclides consisted mainly of core components that were not prepared in JENDL-4.0, the uncertainty analyses were executed for several reactions of U and Pb isotopes composed of the reference and the test zones in fuel assemblies of the KUCA A-core, including capture, elastic scattering, inelastic scattering, fission and (n, 2n) reactions. As shown in Table 7.12, the results of uncertainty in reactivity induced by covariance data were large about the total reactivity of 33.1 pcm, compared with an experimental error around 8 pcm of sample reactivity. The value of total uncertainty was acquired by a square root of the sum of squares for reaction-wise contributions, ignoring the covariance between different nuclides in the sum of squares. Among the nuclides, the reaction-wise contribution was dominant over the capture (19.4 pcm) and the inelastic scattering (20.0 pcm) reactions of ²³⁵U and ²⁰⁶Pb, respectively, shown in Table 7.12. A large contribution was attributable to the sensitivity coefficients of ²³⁵U capture and fission reactions (Fig. 7.18). Also, the reaction-wise contribution of ^{207, 208}Pb inelastic scattering reactions was observed to obtain meaningful values (9.0 pcm).

Table 7.12 Reaction-wise uncertainty contribution [pcm] to changes in sample reactivity induced by covariance data of JENDL-4.0 (Ref. [2])

Fig. 7.18

Sensitivity coefficients of ²³⁵U fission and capture cross sections (JENDL-4.0) (Ref. [2])

For additional study on uncertainty, close attention was paid to the reliability of Pb isotope covariance data of JENDL-4.0 through a comparison between JENDL-4.0 and another library, such as JENDL-3.3, ENDF/B-VII.0 or JEFF-3.1. For a comparison with JENDL-3.3 shown in Fig. 7.19a, contributions of the inelastic scattering cross sections of ^{206, 207}Pb isotopes were found to remarkably exceed the standard deviation evaluated by JENDL-4.0. This tendency was demonstrated mainly with the energy breakdown of reactivity and the difference of microscopic cross sections, with respect to the Pb isotope inelastic scattering reactions, as shown in Fig. 7.19b. This was also the same tendency as the sensitivity coefficients discussed in Sect. 7.3. With ENDF/B-VII.0 and JEFF-3.1, the tendency was not found to be greatly different from JENDL-4.0 as shown in Figs. 7.19c, d, respectively, except for the capture reactions of ^{204, 207}Pb isotopes. Although most cross-section data of Pb isotopes are the same in both ENDF/B-VII.0 and JEFF-3.1, a notable difference in ²⁰⁸Pb inelastic scattering cross sections was observed between the two libraries, through a comparison with the standard deviation by JENDL-4.0.

Fig. 7.19

Reactivity contributions of Pb isotope reactions induced by uncertainties (The error bars indicate the standard deviation evaluated by JENDL-4.0.) (Ref. [2])

7.4.2.2 Cross-Section Adjustment Method

As discussed in Sect. 7.4.2.1, the uncertainty induced by covariance data was compared with that of sample reactivity obtained by the experiments. In this section, the effect of decreasing uncertainty induced by the nuclear data was investigated by the cross-section adjustment method shown in Eqs. (7.30) and (7.31), on calculated reactivity. Here, the uncertainty induced by the analyses was assumed to be null, in order to estimate the maximum effect of decreasing uncertainty on the calculated reactivity. The cross-section adjustment with U and Pb isotopes was considered useful analyses in that the effects of covariance data (U and Pb isotopes) were significant, although the covariance data of H, C and Al isotopes could give inadequate results of the effect on the evaluation of uncertainty.

As shown in Table 7.13, the effect of decreasing uncertainty on the calculated reactivity was significant in ²³⁵U and Pb isotopes. Generally, the effect of decreasing uncertainty regards as becoming large, when errors induced by both experimental and numerical analyses are compared with smaller errors of uncertainty induced by covariance data. In the analyses, the cross-section adjustment method was useful for decreasing the uncertainty, demonstrating a large uncertainty over 30 pcm induced by nuclear data of JENDL-4.0 toward experimental uncertainty of 7 pcm. As a representative example, the C/E value of sample worth reactivity in Case 4 shown in Table 7.11 was greatly improved over 10% shown in Table 7.14, applying the cross-section adjustment method to the uncertainty analyses. Additionally, the C/E values of sample reactivity in Cases 1 through 3 shown in Table 7.10 were remarkably improved to around 5% error with the use of the results of Case 4.

Table 7.13 Reaction-wise uncertainty contribution [pcm] to changes in sample reactivity induced by nuclear data of JENDL-4.0 (Ref. [2])

Table 7.14 Results of C/E values of sample worth reactivity in Case 4 before and after application of cross-section adjustment method (Ref. [2])

7.4.3 Bismuth Isotope

7.4.3.1 Uncertainty

Uncertainty analyses by the UNCERTAINTY code of the MARBLE system were conducted with the use of JENDL-4.0 covariance data (107-energy-group). Since the covariance data of H, C and Al nuclides consisted mainly of core components that are not provided in JENDL-4.0, the uncertainty was analyzed for several reactions of ²⁰⁹Bi, ²³⁵U and ²³⁸U, including capture, elastic scattering, inelastic scattering, fission and (n, 2n) reactions, comprising reference and test fuel assemblies of the KUCA A-core. Nonetheless, among the covariance data of ²⁰⁹Bi, inelastic scattering reactions were only prepared in JENDL-4.0. As shown in Table 7.15, the results of uncertainty induced by covariance data were large, with total reactivity of 24.4 pcm, compared with the experimental error around 3 pcm of sample reactivity worth (Table 7.8). The value of total uncertainty was acquired by the square root of the sum of squares of reaction-wise contributions, disregarding the covariance between different nuclides in the sum of squares. Among the nuclides, the reaction-wise contribution was dominant mainly over the capture (19.4 pcm) and fission (9.7 pcm) reactions of ²³⁵U, and reasonable in the inelastic scattering reactions (10.0 pcm) of ²⁰⁹Bi. In other words, non-negligible contribution of ²⁰⁹Bi inelastic scattering reactions was observed in the uncertainty analyses of Bi sample reactivity worth.

Table 7.15 Reaction-wise contribution [pcm] to changes in Bi sample reactivity worth (Case 4) induced by covariance data of JENDL-4.0 (Ref. [3])

7.4.3.2 Comparative Study on Bi and Pb

Bi sample reactivity worth experiments were considered successfully carried out from the viewpoint of the reproducibility of previous Pb sample reactivity worth experiments, since the measured excess reactivity of the Al reference core was compared with the Bi and Pb experiments under the same condition, as shown in Table 7.16. With the combined use of experimental and numerical results, a comparative study on Bi and Pb sample reactivity worth was instrumental in examining the neutron characteristics of Pb–Bi coolant material in the actual ADS experimental facility.

Table 7.16 Comparison of the results of measured excess reactivities between Bi and Pb test cores (Ref. [3])

In terms of the absolute values of sample reactivity worth shown in Table 7.16, the difference between Bi and Pb sample reactivity worth clearly emphasized the significance of the characteristics of the actual ADS facility attributed to the reactivity effect. Interestingly, on the basis of the neutronics of Pb–Bi, an ADS with a Pb–Bi coolant core could exactly be analyzed by nuclear design calculations. Additionally, from the results of the uncertainty of Bi and Pb isotopes shown in Table 7.17, the impact of Bi induced by nuclear covariance data was considered small compared with that of the total contribution of Pb isotopes, and invaluable in understanding the reason for choosing Pb–Bi as coolant material in ADS.

Table 7.17 Comparison of reaction-wise contributions [pcm] between Bi and Pb (Ref. [6]) sample reactivity worth (Case 4) induced by covariance data of JENDL-4.0 (Ref. [3])

7.5 Conclusion

The Pb sample reactivity worth experiments were carried out at KUCA to examine the uncertainties of cross sections of Pb and other isotopes. The comparison between the experiments and the calculations by MCNP6.1 with JENDL-3.3, JENDL-4.0, ENDF/B-VII.0 and JEFF-3.1 libraries revealed as follows: The library update from JENDL-3.3 to JENDL-4.0 demonstrated that the difference between Pb isotopes was dominant in the comparative study, through the experimental analyses of sample reactivity by the MCNP approach. Moreover, JENDL-4.0 revealed a slight difference from ENDF/B-VII.0 in all the Pb isotopes and ²⁷Al, and from JEFF-3.1 in ²³⁸U and ²⁷Al. For the Bi sample reactivity worth, the comparison between the experiments and the calculations by MCNP6.1 with JENDL-4.0 revealed the importance of the effect of criticality bias on the precision of numerical simulations.

Sensitivity and uncertainty analyses of Pb isotope cross sections were conducted with the combined use of sample reactivity experiments carried out at KUCA and numerical simulations by the SRAC2006 and MARBLE code systems. The experimental sample reactivity was compared with the calculated one by the deterministic approach with the covariance data of JENDL-4.0 as follows: A series of sensitivity and uncertainty analyses demonstrated the reliability of Pb isotope cross-section data of JENDL-4.0, such as the uncertainty of the covariance data, compared with JENDL-3.3, ENDF/B-VII.0 and JEFF-3.1 libraries. Additionally, the numerical results revealed the applicability of sensitivity and uncertainty analyses to the thermal neutron spectrum cores, such as the KUCA core, demonstrating the improvement of calculation results induced by the cross-section adjustment.

For the Bi isotope, sensitivity coefficients of the Bi isotope were relatively small with the comparison of ²⁷Al, ²³⁵U and ²³⁸U comprising of fuel plates and core components. Uncertainty induced by Bi cross sections demonstrated a reasonable result of the Bi sample reactivity worth. From the results of Bi isotope uncertainty, the comparative study on Bi and Pb sample reactivity worth was instrumental in emphasizing the neutronics and the impact of Pb–Bi coolant material in ADS.