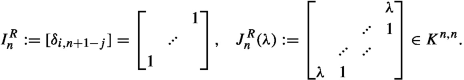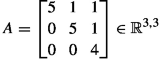Die Jordan- und Frobenius-Normalform

Zusammenfassung

In diesem Kapitel benutzen wir die Theorie der Dualität, um die Eigenschaften eines Endomorphismus f auf einem endlichdimensionalen Vektorraum $\mathcal {V}$ genauer zu untersuchen. Hierbei geht es uns insbesondere um die algebraische und geometrische Vielfachheit aller Eigenwerte von f und die Charakterisierung der entsprechenden Eigenräume. Unsere Strategie in dieser Untersuchung ist, den Vektorraum $\mathcal {V}$ so in eine direkte Summe f-invarianter Unterräume zu zerlegen, dass bei einer geeigneten Wahl von Basen in den jeweiligen Unterräumen die Eigenschaften von f anhand der entsprechenden Matrixdarstellung offensichtlich werden. Diese Idee führt uns auf die Jordan-Normalform von Endomorphismen und Matrizen, die existiert, wenn das charakteristische Polynom von f bzw. A in Linearfaktoren zerfällt. Wegen ihrer großen Bedeutung für die Theorie der Linearen Algebra hat es seit ihrer Entdeckung im 19. Jahrhundert zahlreiche weitere Herleitungen der Jordan-Normalform mit den unterschiedlichsten mathematischen Hilfsmitteln gegeben. Unser Zugang mit der Dualitätstheorie basiert auf der Arbeit [Pta56] von Vlastimil Pták (1925–1999).Mit der gleichen Strategie leiten wir in diesem Kapitel auch die Frobenius-Normalform von Endomorphismen und Matrizen her. Im Gegensatz zur Jordan-Normalform existiert die Frobenius-Normalform selbst dann, wenn f bzw. A keine Eigenwerte besitzt.

Aufgaben

(In den folgenden Aufgaben ist K stets ein beliebiger Körper.)

• 16.1 Beweisen Sie Lemma 16.1 (1).

• 16.2 Beweisen Sie Lemma 16.6 (1).

• 16.3 Seien

  $$A=\begin{bmatrix}0 &{} 1 &{} 1\\ 1 &{} 0 &{} 1\\ 1 &{} 1 &{} 0\end{bmatrix}\in \mathbb {R}^{3,3}, \quad v_1=\begin{bmatrix}1 \\ 1 \\ 1\end{bmatrix}\in \mathbb {R}^{3,1},\quad v_2=\begin{bmatrix}0 \\ 1 \\ 1\end{bmatrix}\in \mathbb {R}^{3,1}.$$

  Bestimmen Sie die Krylov-Räume ${\mathcal {K}}_j(A,v_i)$, $i=1,2$, für alle $j\in \mathbb {N}$.

• 16.4 Sei $\mathcal {V}$ ein endlichdimensionaler K-Vektorraum, $f \in {\mathcal {L}}(\mathcal {V},\mathcal {V})$, $v\in \mathcal {V}$ und $\lambda \in K$. Zeigen Sie, dass ${\mathcal {K}}_{j}(f,v)={\mathcal {K}}_{j}(f-\lambda {{\,\textrm{Id}\,}}_\mathcal {V},v)$ für alle $j\in \mathbb {N}$ gilt. Folgern Sie, dass der Grad von v bezüglich f gleich dem Grad von v bezüglich $f-\lambda {{\,\textrm{Id}\,}}_\mathcal {V}$ ist.

• 16.5 Sei $f\in {\mathcal {L}}(\mathbb {R}^{3,1},\mathbb {R}^{3,1})$ mit $f(e_1)=-e_1$, $f(e_2)=e_2+e_3$, $f(e_3)=-e_3$ gegeben.

  • (a) Bestimmen Sie das charakteristische Polynom $P_f$ und eine Basis des Eigenraums $\mathcal {V}_f(-1)$.

  • (b) Zeigen Sie, dass $\dim ({\mathcal {K}}_3(f,v))\le 2$ für jedes $v\in \mathbb {R}^{3,1}$ gilt.

• 16.6 Beweisen Sie Lemma 16.16.

• 16.7 Sei $\mathcal {V}$ ein endlichdimensionaler euklidischer oder unitärer Vektorraum und sei $f\in {\mathcal {L}}(\mathcal {V},\mathcal {V})$ selbstadjungiert und nilpotent. Zeigen Sie, dass dann $f=0$ ist.

• 16.8 Sei $\mathcal {V}\ne \{0\}$ ein endlichdimensionaler K-Vektorraum, sei $f \in {\mathcal {L}}(\mathcal {V},\mathcal {V})$ nilpotent vom Grad m und $P_f$ zerfalle in Linearfaktoren. Zeigen Sie folgende Aussagen:

  • (a) Es gilt $P_f = t^n$ mit $n=\dim (\mathcal {V})$.

  • (b) Es gilt $M_f = t^m$.

  • (c) Es existiert ein Vektor $v \in \mathcal {V}$ vom Grad m bezüglich f.

  • (d) Für jedes $\lambda \in K$ gilt $M_{f-\lambda {{\,\textrm{Id}\,}}_\mathcal {V}} = (t+\lambda )^m$.

• 16.9 Sei $\mathcal {V}$ ein endlichdimensionaler $\mathbb {C}$-Vektorraum und seien $f,g \in {\mathcal {L}}(\mathcal {V},\mathcal {V})$ zwei kommutierende nilpotente Endomorphismen. Zeigen Sie, dass dann $f+g$ auch nilpotent ist.

• 16.10 Sei $\mathcal {V}$ ein endlichdimensionaler K-Vektorraum und $f \in {\mathcal {L}}(\mathcal {V},\mathcal {V})$. Zeigen Sie folgende Aussagen:

  • (a) Es gilt $\text {Kern}(f^j) \subseteq \text {Kern}(f^{j+1})$ für alle $j\ge 0$ und es existiert ein $m\ge 0$ mit $\text {Kern}(f^m) = \text {Kern}(f^{m+1})$. Für dieses m gilt $\text {Kern}(f^m) = \text {Kern}(f^{m+j})$ für alle $j\ge 1$.

  • (b) Es gilt ${{\,\textrm{Bild}\,}}(f^j) \supseteq {{\,\textrm{Bild}\,}}(f^{j+1})$ für alle $j\ge 0$ und es existiert ein $\ell \ge 0$ mit ${{\,\textrm{Bild}\,}}(f^\ell ) = {{\,\textrm{Bild}\,}}(f^{\ell +1})$. Für dieses $\ell$ gilt ${{\,\textrm{Bild}\,}}(f^\ell ) = {{\,\textrm{Bild}\,}}(f^{\ell +j})$ für alle $j\ge 1$.

  • (c) Sind $m, \ell \ge 0$ minimal mit $\text {Kern}(f^m) = \text {Kern}(f^{m+1})$ und ${{\,\textrm{Bild}\,}}(f^\ell ) = {{\,\textrm{Bild}\,}}(f^{\ell +1})$, dann gilt $m = \ell$.

  (Nach Satz 16.5 ist dann $\mathcal {V}= \text {Kern}(f^m) \oplus {{\,\textrm{Bild}\,}}(f^m)$ eine Zerlegung von $\mathcal {V}$ in f-invariante Unterräume.)

• 16.11 Bestimmen Sie die Jordan-Normalform der Matrizen

  $$\begin{aligned} A=\left[ \begin{array}{rrrr} 1 &{} -1 &{} 0 &{} 0 \\ 1 &{} -1 &{} 0 &{} 0 \\ 3 &{} 0 &{} 3 &{} -3 \\ 4 &{} -1 &{} 3 &{} -3 \end{array}\right] \in \mathbb {R}^{4,4}, \quad B = \left[ \begin{array}{rrrrr} 2 &{} 1 &{} 0 &{} 0 &{} 0 \\ -1 &{} 1 &{} 1 &{} 0 &{} 0 \\ -1 &{} 0 &{} 3 &{} 0 &{} 0 \\ -1 &{} -1 &{} 0 &{} 1 &{} 1 \\ -2 &{} -1 &{} 1 &{} -1 &{} 3 \end{array}\right] \in \mathbb {R}^{5,5} \end{aligned}$$

  mit Hilfe des im letzten Abschnitt dieses Kapitels angegebenen Verfahrens. Bestimmen Sie jeweils auch die Minimalpolynome.

• 16.12 Bestimmen Sie die Jordan-Normalform und das Minimalpolynom der linearen Abbildung

  $$\begin{aligned} f:\mathbb {C}[t]_{\le 3}\rightarrow \mathbb {C}[t]_{\le 3},\quad \alpha _0+\alpha _1 t +\alpha _2 t^2 +\alpha _3 t^3\;\mapsto \; \alpha _1+\alpha _2 t+\alpha _3 t^3. \end{aligned}$$

• 16.13 Bestimmen Sie (bis auf die Reihenfolge der Blöcke) alle Matrizen J in Jordan-Normalform mit $P_J = (t+1)^3 (t-1)^3$ und $M_J = (t+1)^2 (t-1)^2$.

• 16.14 Sei $A\in \mathbb {C}^{3,3}$ mit $A^2=2A-I_3$. Bestimmen Sie alle (bis auf die Reihenfolge der Jordan-Blöcke) verschiedenen möglichen Jordan-Normalformen von A.

• 16.15 Seien $\mathcal {V}\ne \{0\}$ ein endlichdimensionaler K-Vektorraum und f ein Endomorphismus auf $\mathcal {V}$, dessen charakteristisches Polynom in Linearfaktoren zerfällt. Zeigen Sie folgende Aussagen:

  • (a) $P_f = M_f$ gilt genau dann, wenn $g(\lambda ,f) = 1$ für alle Eigenwerte $\lambda$ von f ist.

  • (b) f ist genau dann diagonalisierbar, wenn $M_f$ nur einfache Nullstellen besitzt.

  • (c) Eine Nullstelle $\lambda \in K$ von $M_f$ ist genau dann einfach, wenn $\text {Kern}(f-\lambda {{\,\textrm{Id}\,}}_\mathcal {V})=\text {Kern}((f-\lambda {{\,\textrm{Id}\,}}_\mathcal {V})^2)$ ist.

• 16.16 Sei $\mathcal {V}$ ein K-Vektorraum der Dimension 2 oder 3 und sei $f\in {\mathcal {L}}(\mathcal {V},\mathcal {V})$, so dass $P_f$ in Linearfaktoren zerfällt. Zeigen Sie, dass die Jordan-Normalform von f eindeutig durch die Angabe von $P_f$ und $M_f$ bestimmt ist. Warum gilt dies nicht mehr, wenn $\dim (\mathcal {V})\ge 4$ ist?

• 16.17 Beweisen Sie Lemma 16.20.

• 16.18 Zeigen Sie, dass zwei Matrizen $A,B\in K^{n,n}$ genau dann ähnlich sind, wenn sie die gleiche Frobenius-Normalform bzw. die gleichen Invariantenteiler besitzen.

• 16.19 Sei $A \in K^{n,n}$ eine Matrix, deren charakteristisches Polynom in Linearfaktoren zerfällt. Zeigen Sie, dass eine diagonalisierbare Matrix D und eine nilpotente Matrix N existieren mit $A = D + N$ und $D N = N D$.

• 16.20 Sei

  $$A=\begin{bmatrix}\alpha &{} \beta &{} 0\\ \beta &{} 0 &{} 0\\ 0 &{} 0 &{}\alpha \end{bmatrix} \in \mathbb {R}^{3,3}.$$

  • (a) Bestimmen Sie die Eigenwerte von A in Abhängigkeit von $\alpha ,\beta \in \mathbb {R}$.

  • (b) Bestimmen Sie alle $\alpha ,\beta \in \mathbb {R}$ mit $A\notin GL_3(\mathbb {R})$.

  • (c) Bestimmen Sie das Minimalpolynom $M_A$ in Abhängigkeit von $\alpha ,\beta \in \mathbb {R}$.

• 16.21 Sei $A \in K^{n,n}$ eine Matrix, die eine Jordan-Normalform hat. Wir definieren

  

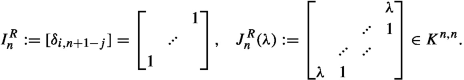
  Zeigen Sie folgende Aussagen:

  • (a) $I_n^R J_n(\lambda ) I_n^R = J_n(\lambda )^T$.

  • (b) A und $A^T$ sind ähnlich.

  • (c) $J_n(\lambda ) = I_n^R J_n^R(\lambda )$.

  • (d) A kann als Produkt zweier symmetrischer Matrizen geschrieben werden.

• 16.22 Sei $\lambda \in K\setminus \{0\}$.

  • (a) Zeigen Sie, dass $J_n(\lambda )$ invertierbar ist mit

    $$ J_n(\lambda )^{-1} = [c_{ij}],\quad c_{ij} = {\left\{ \begin{array}{ll} (-1)^{j-i}\lambda ^{i-j-1},\quad i \le j,\\ 0,\quad i>j. \end{array}\right. } $$

  • (b) Bestimmen Sie eine Jordan-Normalform von $J_n(\lambda )^{-1}$.

  • (c) Sei $A \in K^{n,n}$ eine invertierbare Matrix, deren charakteristisches Polynom in Linearfaktoren zerfällt. Zeigen Sie, dass $A^{-1}$ eine Jordan-Normalform hat und bestimmen Sie diese basierend auf der Jordan-Normalform von A.

• 16.23 Berechnen Sie für die Matrix

  

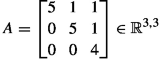
  zwei symmetrische Matrizen $S_1, S_2 \in \mathbb {R}^{3,3}$ mit $A = S_1 S_2$.