Keywords

1 Introduction

Via algorithmic differentiation it is possible to calculate directional derivatives from evaluation procedures of vector valued functions simultaneously with their evaluation at a base point \(x_0\). These evaluations are exact within the limitations of machine precision. An evaluation procedure is a composition of so called elementary functions, which are aggregated as a library in their symbolic form and thus make up the atomic constituents of complex functions. Basically the selection of elementary functions for the library is arbitrary, as long as they comply with assumption (ED) (elementary differentiability, in [3]), meaning that they are at least once Lipschitz-continuously differentiable. In the literature (see e.g. [3, 8]) the following collection is suggested as the quasi-standard for a library:

$$\begin{aligned} \varPhi = \{ +, -, *, /, \sin , \cos , \tan , \cot , \exp , \log , \dots \} \end{aligned}$$

Common software packages such as ADOL-C provide tools for the algorithmic differentiation of functions composed from the contents of this collection.

But many practical problems and most algorithms are not smooth everywhere and thus cannot be modelled via a library that consists solely of a set of functions that comply with (ED). More specifically one is likely to encounter standard functions of computer arithmetic, that are not globally differentiable, e.g. \(\mathbin {\mathrm{abs }}, \max \) and \(\min \). Since

$$\begin{aligned} \max (x,y,z) \equiv \max (\max (x,y),z), \quad \max (x,y) \equiv 0.5 *(x+y+\mathbin {\mathrm{abs }}(x-y)) \end{aligned}$$

\(\max \) and \(\min \) can be expressed in terms of the absolute value function. As shown, this reformulation of \(\max \) and \(\min \) provides us with a very practical handle on the representation of piecewise linearity, since Scholtes proved in [12], that any scalar-valued, real piecewise linear function \(f:\mathbb {R}^n \rightarrow \mathbb {R}\) can be expressed as a finite nesting of \(\max \) and \(\min \) comparisons of linear functions. Here and throughout we use linear in the sense of affine, i.e. allow a constant increment.

Generally any one dimensional piecewise linear function \(f:\mathbb {R}\rightarrow \mathbb {R}\) can be expressed in terms of absolute values. For a given set of points \(\{(x_i,y_i):\, i = 0, \dots , n\}\), where \(x_0 < x_1 < \dots < x_n\), two outer slopes \(s_0,s_{n+1}\) and \(n\) inner slopes \(s_i = (y_i-y_{i-1})/(x_i-x_{i-1})\), we obtain the formula

$$\begin{aligned} y = \frac{1}{2} \left[ y_0+ s_0 (x-x_{0}) + \sum _{i=0}^{n} (s_{i+1}-s_i) \mathbin {\mathrm{abs }}(x-x_{i}) + y_n + s_{n+1} (x-x_n) \right] \end{aligned}$$

where the two linear functions at the beginning and the end can be combined to \( [y_0- s_0 \, x_{0} + y_n - s_{n+1}\, x_n + (s_0 + s_{n+1}) x]/2\). This might be helpful for the purpose of implementation. For example with \(a < b \in \mathbb {R}\) we obtain the cut-off function

$$\begin{aligned} f(x)&= \max (a, \min (x, b)) = 0.5*[a+\mathbin {\mathrm{abs }}(x-a)-\mathbin {\mathrm{abs }}(x-b)+b] \end{aligned}$$

Similar to linear models of smooth functions, piecewise linearizations can be used to approximate piecewise smooth functions [12]. The aim is to extend the principles and techniques of classic algorithmic differentiation in such a way, that these piecewise linear models can be evaluated with the same efficiency, stability and simplicity of data structures as in the linear case. Since the absolute value function is already piecewise linear, it can be modelled by itself. By proposition \(3.1\) from [4] we have for the procedure (introduced in the next chapter) that the error of the piecewise linear approximation is of second order and varies Lipschitz continuously w.r.t. the develo** point.

2 Piecewise Linearization and Abs-Normal Form

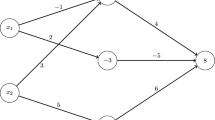
Example 1

Formula, graph and sequential code instruction of an evaluation procedure:

figure a

The \(v_i\) are called intermediate values. The indices are in a dependency relation \(j \prec i\), if there is an edge from \(v_j\) to \(v_i\). In general the values of a sequential code instruction of an evaluation procedure are denoted as a tuple

$$\begin{aligned}{}[v_{1-n}, v_{1-(n-1)}, \dots , v_0, v_1, v_2, \dots , v_i, \dots , v_l] \quad \text { where } \end{aligned}$$
$$\begin{aligned} v_{j-n}&= x_j \qquad \qquad \text {for} \quad j = 1, \dots , n \\ v_i&= \varphi _i(v_j)_{j \prec i}\quad \quad \! \text {for}\quad i = 1, \dots , l \quad \text { and } \quad \varphi \in \varPhi _{\mathbin {\mathrm{abs }}} = \varPhi \cup \{\mathbin {\mathrm{abs }}\} \end{aligned}$$

The values of the piecewise linearization can be evaluated simultaneuosly as increments of the function value by the following set of propagation rules [4] that implicitly defines a second code instruction.

Procedure 1

$$\begin{aligned}{}[\varDelta v_{1-n}, \varDelta v_{1-(n-1)}, \dots , \varDelta v_0, \varDelta v_1, \varDelta v_2, \dots , \varDelta v_i, \dots , \varDelta v_l] \quad \text { where } \end{aligned}$$

for \(\quad j = 1,\dots ,n: \quad \varDelta v_{j-n} =\varDelta x_j \quad \) and for \(\quad i = 1,\dots ,l:\)

Then the \(k\)-th component of the piecewise linearization is determined by:

$$\begin{aligned} y_k = v_{l-m+k} + \varDelta v_{l-m+k} \end{aligned}$$

The overall costs are at most four times of those of a function evaluation [3].

So far we have a method for a small number of evaluations at some basepoints. But for the purposes of integration, solving ODEs, optimization and solving piecewise linear equation systems (see [4, 5]) we need a suitable data structure for a large number of evaluations of a single piecewise linearization. A general nonlinear concept of Barton and Khan from [6] combined with ta** technology leads to the abs-normal form:

Definition 1

For \(Z \in \mathbb {R}^{s\times n}, L\in \mathbb {R}^{s\times s}, J \in \mathbb {R}^{m\times n}, Y\in \mathbb {R}^{m\times s}\) matrices, where \(L\) is of strictly lower triangular form and vectors \(c \in \mathbb {R}^s, b\in \mathbb {R}^m\), the system

$$\begin{aligned} \left[ \begin{array}{c} z \\ y \end{array}\right] = \left[ \begin{array}{c} c \\ b \end{array}\right] + \left[ \begin{array}{cc} Z &{} L \\ J &{} Y \end{array}\right] \left[ \begin{array}{c} x \\ |z |\end{array}\right] \end{aligned}$$
(1)

is called abs-normal form. The modulus operation \(|z |\) has to be understood componentwise here. An abs-normal form is called simply switched if \(L=0\).

The components of \(z\) can be evaluated successively, since \(L\) is a strictly lower triangular matrix. The control flow in the evaluation of the abs-normal form is conveniently characterised by the signature vectors and matrices

$$\begin{aligned} \sigma _x \equiv \sigma _z \equiv \mathbin {\mathrm{sign }}(z) \in \{-1,0,1\}^s, \qquad \varSigma _z = \mathbin {\mathrm{diag }}(\sigma _z) \in \{-1,0,1\}^{s\times s} \end{aligned}$$

In particular we will use throughout the identity \(|z |= \varSigma _z z\). Using this relation we can eliminate \(z\) for any given \(x \in \mathbb {R}^n\) and obtain the explicit representation

$$\begin{aligned} F(x) = y =&\overbrace{b + Y\varSigma _\sigma (I-L\varSigma _\sigma )^{-1}c}^{\text {piecewise constant}} + J_\sigma \cdot x \end{aligned}$$
(2)
$$\begin{aligned}&\text {where } J_\sigma = J + Y\varSigma _\sigma (I-L\varSigma _\sigma )^{-1}Z \end{aligned}$$
(3)

On the other hand every piecewise linear function in \(\max \)-\(\min \) expression can be represented in abs-normal form. Thus the abs-normal form is an equivalent characterization of piecewise linear map**s, which is stable w.r.t to perturbationsFootnote 1. Each signature vector \(\sigma \in \{-1,0,1\}^s\) uniquely characterises the polyhedron

$$\begin{aligned} P_\sigma = \{ x \in \mathbb {R}^n \mid \sigma _x = \sigma \} \end{aligned}$$

The collection of these mutually disjoint and relatively open polyhedra forms a so called polyhedral decomposition or skeleton \(\mathcal P\) of \(\mathbb {R}^n\). The restriction of \(F\) to the closure of any \(P_\sigma \in \mathcal P\) is linear (Fig. 1).

Fig. 1.
figure 1

Example of a piecewise linear function and its corresponding polyhedral decomposition

Full size image

Each \(P = P_\sigma \) has a nonempty interior if and only if it is open, in which case we will also refer to \(\sigma \) as open. By continuity all \(\sigma \) that have no zero components are open, but the converse need not be the case. It can be shown, that the \(J_\sigma \) given in (3) are limiting Jacobians in the following sense exactly if \(\sigma \) is open.

For general Lipschitz continuous \(F\) it follows from Rademacher’s Theorem that it has a Frechet derivative \(F^\prime (x)\) at all points in a set \(D_F\), whose complement has the measure zero. The set of limiting Jacobians at any \(x_0 \in \mathbb {R}^n\) is defined as

$$\begin{aligned} \partial ^L F(x_0) = \left\{ \lim _{\begin{array}{c} x \rightarrow x_0 \\ x \in D_F \end{array}} F^\prime (x) \right\} \ne \emptyset \end{aligned}$$

and the set of generalized Jacobians in the sense of Clarke as

$$\begin{aligned} \partial F(x_0) = \mathbin {\mathrm{conv }}(\partial ^L F(x_0)) \end{aligned}$$

The definition of \(\partial ^L F(x_0)\) looks quite nonconstructive and in fact there is no general methodology for evaluating limiting Jacobians since the rules for propagating generalized derivatives are only inclusions. Given the abs-normal form one can compute limiting Jacobians that are also generalized Jacobians of the underlying nonlinear functions by a technique called polynomial escape [4, 6]. The computational complexity is similar to that of the foward mode in the smooth case. Especially for generalized gradients where \(m = 1\) an adaption of the much cheaper reverse mode is under development.

Throughout the remainder of this paper, we will only consider piecewise linear \(F\) in abs-normal form that are square in that \(m=n\). Furthermore we assume w.l.o.g. that the so called smooth part \(J\) is nonsingular. If this is not a priori true one can shift terms by using the identity \(x = \mathbin {\mathrm{abs }}(x+\mathbin {\mathrm{abs }}(x)) - \mathbin {\mathrm{abs }}(x)\). The Schur complement of \(J\) within the abs-normal form is given by \(S = L - ZJ^{-1}Y\). By using the Sherman-Morrison-Woodbury formula we can characterise the nonsingularity of the generalized Jacobian \(J_\sigma \) as follows

$$\begin{aligned} \det (J_\sigma ) = \det (J)\det (I-S\varSigma _\sigma ) \text {, for } \sigma = \sigma _x \in \{-1,0,1\}^s \end{aligned}$$
(4)

Note that the upper half of the abs-normal form, which maps \(x\) onto \(z\), need not be surjective. Hence the map** is maybe partially switched in that some signature vectors \(\sigma \in \{-1,0,1\}^s\) do not arise as \(\sigma _x\) for any \(x\). In other words some \(P_\sigma \) might be empty. On the other hand if the linear map \(Zx\) is surjective, then the abs-normal form must be totally switched in that all \(3^n\) sign combinations of \(\sigma \) with corresponding nonempty \(P_\sigma \) do arise. The following so called complementary piecewise linear map**s are always totally switched, since \(z \in \mathbb {R}^s\) becomes independent and ranges over all of \(\mathbb {R}^s\).

3 Complementary Piecewise Linear Systems and Their Relation to LCPs

In contrast the nonsingularity of the smooth part \(J\) allows the elimination of \(x\) for any given \(z\) and \(y\).

$$\begin{aligned} y = b + Jx + Y |z |\iff x = J^{-1}(y-b) - J^{-1}Y |z |\end{aligned}$$

In view of solving \( F(x) = 0 \) we can set \(y = 0\) or absorb it into \(b\). Then substitution of \(x\) into the upper half yields the complementary piecewise linear map**

$$\begin{aligned} H(z) \equiv (I-S\varSigma _z)z - \hat{c} \text {, where } \hat{c} \equiv c - ZJ^{-1}b \end{aligned}$$

The function \(H:\mathbb {R}^s \rightarrow \mathbb {R}^s\) is still piecewise linear and has the abs-normal form

$$\begin{aligned} \left[ \begin{array}{c} \tilde{z} \\ H(z) \end{array}\right] = \left[ \begin{array}{c} 0 \\ -\hat{c} \end{array}\right] + \left[ \begin{array}{cc} I &{} 0 \\ I &{} -S \end{array}\right] \left[ \begin{array}{c} z \\ |\tilde{z} |\end{array}\right] \end{aligned}$$
(5)

whose Schur complement is again \(S\). Since the new \(L\) vanishes, the complementary piecewise linear map is always simply switched. Moreover the polyhedral decomposition consists entirely of \(2^n\) open orthants and their faces. As shown in [5] this implies that \(H\) is bijective if and only if it is an open map. For general PL functions and in particular the underlying \(F\) we only have the chain of implications [12]

$$\begin{aligned} F \text { is injective } \implies F \text { is open } \implies F \text { is surjective} \end{aligned}$$

Furthermore Scholtes has proven in [12] that piecewise linear maps are open maps if and only if the determinants of all limiting Jacobians have the same sign (are w.l.o.g. positive). The limiting Jacobians of \(H\) are exactly the shifted identities \(I-S\varSigma \) for any \(\varSigma = \mathbin {\mathrm{diag }}(\sigma )\) with \(\sigma \in \{-1,1\}^{s}\). Consequently, coherent orientation of \(H\) occurs if and only if all \(\det (I-S\varSigma )\) are positive, which implies by (4) the coherent orientation of \(F\). Whereas the converse need not be true, i.e. \(F\) may be coherently oriented but \(H\) not.

The problem of solving \(H(z) = 0\), for some \(z\in \mathbb {R}^n\) can be recast as a linear complementarity problem (LCP). It turns out to have the \(P\)-matrix property if and only if \(H\) is coherently oriented [11]. The reformulation requires:

Lemma 1

Let \(M,S \in \mathbb {R}^{s\times s}\) arbitrary, s.t. \((I+S)M = (I-S)\), then

  1. 1.

    \(\det (I+S) \ne 0 \iff \det (I+M) \ne 0\)

  2. 2.

    \( S = (I+M)^{-1}(I-M)\) if \(\det (I+M) \ne 0\)

Proof

$$\begin{aligned} M = [I+S]^{-1}[I-S]&\iff [I+S]\tfrac{1}{2} (I+M) = \tfrac{1}{2}([I+S] + [I-S]) = I \\&\iff S = 2(I+M)^{-1} - I = (I+M)^{-1}(I-M) \qquad \\ \end{aligned}$$

\(\square \)

Now consider two vectors \(0 \le u,w \ge 0\), such that \(z = u-w\) and \(u^\top w = 0\). Then by the upper half of an abs-normal form for \(F\)

$$\begin{aligned} u - w&= c + Zx + L(u+w) \\&= c + \big [ ZJ^{-1}(y-b) - ZJ^{-1}Y(u+w) \big ] + L(u+w) \\&= \hat{c} + S(u+w) \iff (I-S)u = \hat{c} + (I+S)w \\ \iff \qquad w&=u-(I+S)^{-1}\hat{c} \iff w =Mu + q \end{aligned}$$

where \(M \equiv (I+S)^{-1}(I-S) \) and \(q \equiv -(I+S)^{-1}\hat{c}\). Because of the substitution of \(x\), the solutions of this standard LCP \(w = q + Mu\), are solutions of the complementary piecewise linear system \(H\). Any standard LCP \(w = q + Mu\), where \(u,w \ge 0\) and \(u^\top w = 0\), can be rewritten as a complementary piecewise linear equation system as

$$\begin{aligned} z = (I+M)^{-1}(I-M)|z |- 2(I + M)^{-1}q \end{aligned}$$

where \( u = \frac{1}{2} (|z|+ z) \) and \(w = \frac{1}{2} (|z |- z)\). This was proven by Bokhoven in his thesis [1]. To transform the complementary piecewise linear system into an LCP or vice versa one has to compute the Möbius transform of \(S\) or \(M\), respectively. This requires in either case at least implicitly a matrix inversion and several multiplications. Therefore we consider methods for directly solving the original and complementary piecewise linear system possibly even avoiding the explicit computation of \(S = L - ZJ^{-1}Y\).

4 Solving Piecewise Linear Equation Systems

The principal task is to find solutions \(x \in \mathbb {R}^n\), such that \(F(x) = 0 \) with piecewise linear \(F:\mathbb {R}^n \rightarrow \mathbb {R}^n\). A possible nonzero right hand side can be absorbed into the vector \(b\) as described above.

There are several methods developed and discussed in detail in [4, 5]. Some of them solve \(F(x) = 0\) directly, whereas others solve the complementary piecewise linear equation System \(H(z) = 0\). Note that there is a one-to-one solution correspondence between both representations [5]. Now, let us give an overview of some of these methods.

4.1 Full-Step Newton Variants

All continuous piecewise linear functions are known to be semi smooth. Hence the result in [10] ensures local convergence of the full-step iteration

$$\begin{aligned} x_+ = x - J^{-1}F(x) \text {, for }J \in \partial F(x) \end{aligned}$$

to a solution \(x^*\), provided that all generalized Jacobians \(J \in \partial F(x^*)\) are nonsingular. However this condition need not be satisfied even if \(F\) is coherently oriented. Coherent orientation in some vicinity of \(x^*\) means that all limiting Jacobians \( J \in \partial ^LF(x^*) \) are nonsingular, so that the stronger result from [9], where the \(J\) are restricted to be limiting Jacobians, is applicable.

It should be noted that both results apply here in a trivial fashion, since convergence in one step must occur from all points \(x_0\) belonging to polyhedra \(P_\sigma \), whose closure contains \(x^*\). Of course finding such an initial point \(x_0\) requires to resolve all combinatorial issues in advance.

Hence we are more interested in global convergence results. We can guarantee full step convergence for the restricted generalized Newton method in finitely many steps towards the unique solution, if either of the contractivity conditions

$$\begin{aligned} ||I - J_{\sigma }^{-1}J_{\tilde{\sigma }} ||&< 1 \text {, for all } \sigma , \tilde{\sigma }\text { open} \\ \text {or } \qquad ||I - J_{\sigma }J_{\tilde{\sigma }}^{-1} ||&< 1 \text {, for all } \sigma , \tilde{\sigma }\text { open} \end{aligned}$$

is satisfied w.r.t. to some induced matrix norm. The proof can be found in [5]. Either condition is rather strong and implies bijectivity. In terms of the abs-normal form they are implied by the conditions

$$\begin{aligned} \hat{\rho }\equiv ||Z ||||J^{-1} Y ||< 1 - ||L ||\quad \text { and }\quad \frac{\hat{\rho }}{(1-\hat{\rho }- ||L ||)(1-||L ||)} < \frac{1}{2} \end{aligned}$$

As we have already noted suitable \(J_\sigma \) can be computed from the abs-normal form at reasonable expense.

Naturally the generalized Newton method with or without restriction to limiting Jacobians can also be applied to the complementary piecewise linear system, yielding

$$\begin{aligned} z_+ = z - (I-S\varSigma _z)^{-1}H(z) = (I-S\varSigma _z)^{-1}\hat{c} \end{aligned}$$

However, here the local convergence condition that all limiting Jacobians be nonsingular is no weaker than the requirement that all generalized Jacobians be nonsingular. Sufficient for global full-step convergence are either of the following independent conditions

$$\begin{aligned} ||S ||_p < \tfrac{1}{3} \qquad \text { or }\qquad \rho (|S |) < \tfrac{1}{2} \end{aligned}$$

where \(\rho \) denotes the spectral radius and \(|S |\) the componentwise modulus.

If the second condition is satisfied, the calculation can be organized such that the whole solution process requires only \(\tfrac{1}{3} s^3\) operations, just like a Gaussian elimination in the smooth linear case.

4.2 Piecewise Newton

Rather than taking full steps based on a local linearization one may restrict steps to stay within the closure of one polyhedron \(P_\sigma \). This requires some pivoting and active set managament familiar from Lemke type algorithms for LCPs. For a comparitive study of the two approaches see the dissertation of T. Munson [7]. In [4] it was observed that coherent orientation implies, that the fibres

$$\begin{aligned}{}[x_0] \equiv \{x \in \mathbb {R}^n:\, F(x) = \lambda F(x_0),\, 0 < \lambda \in \mathbb {R}\} \end{aligned}$$

are bifurcation-free piecewise linear paths for almost all \(x_0 \in \mathbb {R}^n\). Then their closure contains a solution. Even in the case of singular fibres, there are strategies to reduce the residual towards a solution. An implementation is currently under development.

4.3 Modulus Algorithm

Checking \(F\) for surjectivity or openess is NP-hard, because there may be \(2^n\) possible determinants \(\det (J_\sigma )\), for \(\sigma = \sigma _x\). An easier verifiable property is smooth dominance.

Definition 2

\(F : \mathbb {R}^n \rightarrow \mathbb {R}^n\) in abs-normal form is called smooth dominant, if for some nonsingular diagonal matrix \(D\) and a \(p \in [1, \infty ]\)

$$\begin{aligned} ||DSD^{-1}||_p < 1 \end{aligned}$$

Smooth dominant abs-normal forms are always injective [5]. Nevertheless there are many practical problems which satisfy this condition.

In [2] Brugnano and Casulli consider unilateral constraints

$$\begin{aligned} \text {solve }\max (0,x) + Tx = -e/2 \end{aligned}$$

where \(T \in \mathbb {R}^{n \times n}\) is an irreducible, symmetric, positive semidefinite matrix and \(x,e \in \mathbb {R}^n\) vectors. This class of problems is piecewise linear and its abs-normal forms are smooth dominant. Electrical engineers considered piecewise linear function as models of electrical circuits since the \(50\)’s of the last century. For example Bokhoven discussed those models in his dissertation [1] and introduced the iteration

$$\begin{aligned} z_+ = S|z |- \hat{c} \end{aligned}$$

whose convergence follows from smooth dominance, by the Banach fix point theorem. In our experience the modulus iteration is robust, but rather slow.

4.4 Alternating Block Seidel Iteration

Another fixed point iteration which has the potential of being significantly faster, is the following block Seidel scheme from [5]. Solving alternatingly the upper half for \(z\) and the lower half for \(x\), we obtain \( z_+ = h_z(h_x(z))\), where

$$\begin{aligned} h_z:\,&\mathbb {R}^n \rightarrow \mathbb {R}^s&h_z(x)&= (I-L\varSigma _x)^{-1}(c+Zx) \\ h_x:\,&\mathbb {R}^s \rightarrow \mathbb {R}^n&h_x(z)&= -J^{-1}b - J^{-1}Y\varSigma _z z \end{aligned}$$

The convergence of this method to the unique solution is ensured [5], if

$$\begin{aligned} ||S ||_p \le ||L ||_p + ||ZJ^{-1}Y||_p < 1 \end{aligned}$$

for some suitable \(p\) where positive diagonal scaling may be applied.

5 Conclusion and Outlook

We gave a short introduction to basic techniques of automatic differentiation and methods for the modelling of piecewise smooth functions via piecewise linearization with a second order error. We also discussed the solvabillity of the resulting equation systems in abs-normal form, by finitely convergent Newton variants or linearly convergent fix point solvers. Currently we are working on hybrid algorithms to obtain stable global and fast local convergence. They will then be used in the inner loop of a piecewise smooth equation solver by successive piecewise linearization. A related task to equation solving are the (un)constrained optimization of piecewise smooth objectives and the numerical integration of initial value problems with Lipschitzian right hand sides. Common utillities for manipulating abs-normal forms are developed as the linear algebra package PLAN-C, which uses abs-normal forms as objects.