Abstract
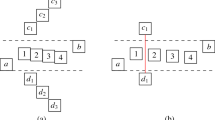
Orthogonal ray graphs are the intersection graphs of horizontal and vertical rays (i.e. half-lines) in the plane. If the rays can have any possible orientation (left/right/up/down) then the graph is a 4-directional orthogonal ray graph (4-DORG). Otherwise, if all rays are only pointing into the positive x and y directions, the intersection graph is a 2-DORG. Similarly, for 3-DORGs, the horizontal rays can have any direction but the vertical ones can only have the positive direction. The recognition problem of 2-DORGs, which are a nice subclass of bipartite comparability graphs, is known to be polynomial, while the recognition problems for 3-DORGs and 4-DORGs are open. Recently it has been shown that the recognition of unit grid intersection graphs, a superclass of 4-DORGs, is NP-complete. In this paper we prove that the recognition problem of 4-DORGs is polynomial, given a partition {L,R,U,D} of the vertices of G (which corresponds to the four possible ray directions). For the proof, given the graph G, we first construct two cliques G 1,G 2 with both directed and undirected edges. Then we successively augment these two graphs, constructing eventually a graph \(\widetilde{G}\) with both directed and undirected edges, such that G has a 4-DORG representation if and only if \(\widetilde{G}\) has a transitive orientation respecting its directed edges. As a crucial tool for our analysis we introduce the notion of an S-orientation of a graph, which extends the notion of a transitive orientation. We expect that our proof ideas will be useful also in other situations. Using an independent approach we show that, given a permutation π of the vertices of U (π is the order of y-coordinates of ray endpoints for U), while the partition {L,R} of V ∖ U is not given, we can still efficiently check whether G has a 3-DORG representation.
This work was partially supported by (i) the DFG ESF EuroGIGA projects COMPOSE and GraDR, (ii) the EPSRC Grant EP/K022660/1, (iii) the EPSRC Grant EP/G043434/1, and (iv) the Berlin Mathematical School.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Cabello, S., Cardinal, J., Langerman, S.: The clique problem in ray intersection graphs. In: Epstein, L., Ferragina, P. (eds.) ESA 2012. LNCS, vol. 7501, pp. 241–252. Springer, Heidelberg (2012)
Chalopin, J., Gonçalves, D.: Every planar graph is the intersection graph of segments in the plane: extended abstract. In: Proc STOC 2009, pp. 631–638 (2009)
Coppersmith, D., Winograd, S.: Matrix multiplication via arithmetic progressions. Journal of Symbolic Computation 9(3), 251–280 (1990)
Estivill-Castro, V., Noy, M., Urrutia, J.: On the chromatic number of tree graphs. Discrete Mathematics 223(1-3), 363–366 (2000)
Feder, T., Hell, P., Huang, J.: List homomorphisms and circular arc graphs. Combinatorica 19, 487–505 (1999)
Felsner, S.: 3-interval irreducible partially ordered sets. Order 11, 12–15 (1994)
Felsner, S., Habib, M., Möhring, R.H.: On the interplay of interval dimension and dimension. SIAM Journal on Discrete Mathematics 7, 32–40 (1994)
Habib, M., Paul, C., Viennot, L.: Partition refinement techniques: An interesting algorithmic tool kit. Int. J. Found. Comput. Sci. 10(2), 147–170 (1999)
Hartman, I.-A., Newman, I., Ziv, R.: On grid intersection graphs. Discrete Mathematics 87(1), 41–52 (1991)
Kratochvíl, J.: A special planar satisfiability problem and a consequence of its NP-completeness. Discrete Applied Mathematics 52(3), 233–252 (1994)
Kratochvíl, J., Matoušek, J.: NP-hardness results for intersection graphs. Commentationes Mathematicae Universitatis Carolinae 30(4), 761–773 (1989)
Kratochvíl, J., Matoušek, J.: Intersection graphs of segments. J. Comb. Theory, Ser. B 62(2), 289–315 (1994)
McConnell, R.: Linear-time recognition of circular-arc graphs. In: Proceedings of the 42nd IEEE Symposium on Foundations of Computer Science, pp. 386–394 (2001)
Mustaţă, I., Pergel, M.: Unit grid intersection graphs: recognition and properties (in preparation, 2013)
Otachi, Y., Okamoto, Y., Yamazaki, K.: Relationships between the class of unit grid intersection graphs and other classes of bipartite graphs. Discrete Applied Mathematics 155(17), 2383–2390 (2007)
Rao, W., Orailoglu, A., Karri, R.: Logic map** in crossbar-based nanoarchitectures. IEEE Design & Test of Computers 26(1), 68–77 (2009)
Richerby, D.: Interval bigraphs are unit grid intersection graphs. Discrete Mathematics, 1718–1719 (2009)
Shrestha, A., Tayu, S., Ueno, S.: Orthogonal ray graphs and nano-PLA design. In: Proc. IEEE ISCAS 2009, pp. 2930–2933 (2009)
Shrestha, A.M.S., Tayu, S., Ueno, S.: On orthogonal ray graphs. Discrete Appl. Math. 158(15), 1650–1659 (2010)
Soto, J.A., Telha, C.: Jump number of two-directional orthogonal ray graphs. In: Günlük, O., Woeginger, G.J. (eds.) IPCO 2011. LNCS, vol. 6655, pp. 389–403. Springer, Heidelberg (2011)
Trotter, W.: Combinatorics and Partially Ordered Sets. The Johns Hopkins University Press (1992)
Uehara, R.: Simple geometrical intersection graphs. In: Nakano, S.-I., Rahman, M. S. (eds.) WALCOM 2008. LNCS, vol. 4921, pp. 25–33. Springer, Heidelberg (2008)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2013 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Felsner, S., Mertzios, G.B., Musta, I. (2013). On the Recognition of Four-Directional Orthogonal Ray Graphs. In: Chatterjee, K., Sgall, J. (eds) Mathematical Foundations of Computer Science 2013. MFCS 2013. Lecture Notes in Computer Science, vol 8087. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-40313-2_34
Download citation
DOI: https://doi.org/10.1007/978-3-642-40313-2_34
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-40312-5
Online ISBN: 978-3-642-40313-2
eBook Packages: Computer ScienceComputer Science (R0)