Abstract
This chapter further develops Background Independence and the Problem of Time at the classical level for approaches in which spacetime is primary (a position we started in Chap. 10). We consider spacetime diffeomorphisms, and contrast the corresponding Spacetime Relationalism with the dynamically primary approaches’ Temporal and Configurational Relationalism. Given that spacetime diffeomorphisms generators close, we also consider associated notions of spacetime or path (alias Bergmann) observables. We introduce the space of spacetimes and the space of general relativity solutions. Finally, we give the first of two parts of an outline of Bergmann’s work and its expansion by Pons, Salisbury and Sundermeyer. This involves using larger groups than the spacetime diffeomorphisms, such for now the diffeomorphism-induced gauge group.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
One might moreover consider a notion of weak equality instead, now meaning up to terms containing the generators. Also, one is only to select subsets of generators which close algebraically. The Jacobi identity applying to all Lie brackets, these
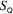 are also guaranteed to close as a Lie algebra.
are also guaranteed to close as a Lie algebra. - 2.
Infinitesimal transformations \(\vec{X} \rightarrow \vec{\widetilde{X}}\) can be written as \(\vec{X} - \vec{\widetilde{X}} = \vec{\epsilon }\). Viewed as solutions in terms of Hamiltonian variables, the right hand side functions here are so-called descriptors: a fairly standard Gauge Theoretic notion, see e.g. [13, 134]). For GR, descriptors are of the particular form \(\vec{\upnu }(\vec{X}; \boldsymbol{\**}(\vec{X})]\). Here \(\boldsymbol{\**}\) denotes the set of dynamical fields \(\boldsymbol{\uppsi}\) and \(\mathbf{h}\); note that this specifically excludes the lapse \(\upalpha \) and shift \(\upbeta^{i}\). Dittrich’s \(\mbox{V}^{\mu }\) in (25.30) and Chap. 27.5’s Weyl scalars can be viewed as particular cases of descriptors.
- 3.
See [721] for the sense in which this is ‘induced’. \(\mathit{Digg}(\mathfrak{m})\) might also be denoted \(BK(\mathfrak{m})\) after Bergmann and Komar [134], though they themselves referred to it as the ‘\(Q\)-group’. Physicists Josep Maria Pons, Donald Salisbury and Kurt Sundermeyer prefer to use the Bergmann–Komar name for the subsequent projected version of this group that introduced in Chap. 32.4. Incidentally, the existence of this larger invariance group does not by itself dictate that it is the gauge group. [This is one example of Sect. 27.7’s matter, as well as the more specific reason to use the projected version.]
- 4.
For suppose that a model, with maximal symmetry group
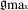 , fails to capture some physically meaningful features which themselves do not respect
, fails to capture some physically meaningful features which themselves do not respect 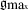 . Then there is a smaller choice group, ℌ, which happens to be more physical. Moreover, one way of finding it and the missing physically meaningful features is to consider not just
. Then there is a smaller choice group, ℌ, which happens to be more physical. Moreover, one way of finding it and the missing physically meaningful features is to consider not just 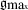 for the original model, but rather it and all its subgroups. This is out of the possibility that one or more of these are more physically valuable than
for the original model, but rather it and all its subgroups. This is out of the possibility that one or more of these are more physically valuable than 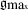 itself.
itself. - 5.
Moreover, extending \(\mathfrak{q}\) or its spacetime equivalent may further enlarge the largest symmetry group ℌ, break ℌ or both at once. I.e. extend the subgroup that survives a breaking in a different way from the original ℌ.
References
Anderson, J.L.: Principles of Relativity Physics. Academic Press, New York (1967)
Bergmann, P.G.: “Gauge-invariant” variables in general relativity. Phys. Rev. 124, 274 (1961)
Bergmann, P.G., Komar, A.: The coordinate group symmetries of general relativity. Int. J. Theor. Phys. 5, 15 (1972)
Fischer, A.E.: The theory of superspace. In: Carmeli, M., Fickler, S.I., Witten, L. (eds.) Relativity, Proceedings of the Relativity Conference in the Midwest, Cincinnati, Ohio, 2–6 June 1969 Plenum, New York (1970)
Géhéniau, J., Debever, R.: Les Quatorze Invariants de Courbure de l’Espace Riemannien a Quatre Dimensions [The 14 curvature invariants of 4-\(d\) Riemannian space]. Helv. Phys. Acta Suppl. 4, 101 (1956)
Giulini, D.: Some remarks on the notions of general covariance and background independence. In: Stamatescu, I.O. (ed.) An Assessment of Current Paradigms in the Physics of Fundamental Interactions. Lect. Notes Phys., vol. 721, p. 105 (2007). ar**v:gr-qc/0603087
Isham, C.J.: Aspects of Quantum Gravity. Lectures Given at Conference: C85–07-28.1 (Scottish Summer School 1985:0001), available on KEK archive
Isham, C.J.: Canonical quantum gravity and the problem of time. In: Ibort, L.A., Rodríguez, M.A. (eds.) Integrable Systems, Quantum Groups and Quantum Field Theories. Kluwer Academic, Dordrecht (1993). gr-qc/9210011
Muga, G., Sala Mayato, R., Egusquiza, I. (eds.): Time in Quantum Mechanics, vol. 1. Springer, Berlin (2008)
Muga, G., Sala Mayato, R., Egusquiza, I. (eds.): Time in Quantum Mechanics, vol. 2. Springer, Berlin (2010)
Penrose, R., Rindler, W.: Spinors and Space-Time: Volume 1, Two-Spinor Calculus and Relativistic Fields. Cambridge University Press, Cambridge (1984)
Pons, J.M., Salisbury, D.C., Shepley, L.C.: Gauge transformations in the Lagrangian and Hamiltonian formalisms of generally covariant theories. Phys. Rev. D 55, 658 (1997). gr-qc/9612037
Samuel, J.: Is Barbero’s Hamiltonian formulation a gauge theory of Lorentzian gravity? Class. Quantum Gravity 17, L141 (2000). gr-qc/0005095
Stewart, J.M.: Advanced General Relativity. Cambridge University Press, Cambridge (1991)
Szekeres, P.: The gravitational compass. J. Math. Phys. 6, 1387 (1965)
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this chapter
Cite this chapter
Anderson, E. (2017). Spacetime Relationalism. In: The Problem of Time. Fundamental Theories of Physics, vol 190. Springer, Cham. https://doi.org/10.1007/978-3-319-58848-3_27
Download citation
DOI: https://doi.org/10.1007/978-3-319-58848-3_27
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-58846-9
Online ISBN: 978-3-319-58848-3
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)


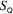 are also guaranteed to close as a Lie algebra.
are also guaranteed to close as a Lie algebra.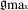 , fails to capture some physically meaningful features which themselves do not respect
, fails to capture some physically meaningful features which themselves do not respect 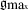 . Then there is a smaller choice group, ℌ, which happens to be more physical. Moreover, one way of finding it and the missing physically meaningful features is to consider not just
. Then there is a smaller choice group, ℌ, which happens to be more physical. Moreover, one way of finding it and the missing physically meaningful features is to consider not just 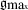 for the original model, but rather it and all its subgroups. This is out of the possibility that one or more of these are more physically valuable than
for the original model, but rather it and all its subgroups. This is out of the possibility that one or more of these are more physically valuable than 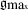 itself.
itself.