Identification of Causal Mediation Models with an Unobserved Pre-treatment Confounder

Abstract

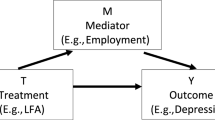
In this paper, we discuss identifiability of mediation, direct and indirect effects of treatment on outcome. The mediation effects are represented by a causal mediation model which includes an unobserved confounder (i.e., a common cause of the mediator and the outcome variable), and the direct and indirect effects are represented by the mediation effects. Without requiring the sequential ignorability assumption or the exclusion restriction assumption (i.e., the absence of direct effect of treatment on outcome), we require that only treatment is randomized and that the degree of equation nonlinearity for the treatment effect on the mediator is higher than that for the outcome. If the requirement of nonlinearity degree is not satisfied, we may use a covariate as an instrumental variable to improve the identifiability. In this paper, we focus on the identifiability of parameters, although, to illustrate our identifiability results, we describe estimation approaches. The simulations show good estimation performance by our approach compared to the standard mediation approach.

Appendices

Appendix 1: Proof of Theorem 1

We separately show the necessity and sufficiency for the identifiability of parameters in model (13.7). For necessity, suppose that the non-linearity condition does not hold, that is, | ρ(E(M | X), X) |  = 1. This implies that there exist some a ₀ and a ₁ satisfying E(M | X) = a ₁ X + a ₀ almost everywhere. Then from the model (13.7) we have

$$\displaystyle\begin{array}{rcl}E(Y \vert X)& =& b_{0} + b_{1}E(M\vert X) + b_{2}X{}\\ & =& (b_{0} + a_{0}b_{1}) + (a_{1}b_{1} + b_{2})X. {}\\\end{array}$$

The above equation implies that Y ismarginally linear with respect to X.For this linear model, only the intercept(b ₀ + a ₀ b ₁) and the slope(a ₁ b ₁ + b ₂) are identifiable as awhole, while parameters b ₀,b ₁, andb ₂cannot be distinguished each other.

For sufficiency, if M is not marginally linearly related with respect to X, then we can find 3 levels: x ₁, x ₂, and x ₃, which satisfy [E(M | x ₁) − E(M | x ₂)]∕(x ₁ − x ₂) ≠ [E(M | x ₂) − E(M | x ₃)]∕(x ₂ − x ₃). Hence the matrix in (13.10) has full rank. Thus parameters b ₁ and b ₂ can be identified, and then parameter b ₀ can be identified from b ₀ = E(Y | x _i ) − b ₁ E(M | x _i ) − b ₂ x _i .

Appendix 2: Proof for Theorem 2

For sufficiency, when E(M | X, Z) ≠ cX +ψ(Z), there are two situations: (i) E(M | X, Z) = Ψ(X) +ψ(Z), where Ψ(⋅ ) is a nonlinear function of X; (ii) E(M | X, Z) is not additive with respect to X and Z.

For situation (i), since Ψ(⋅ ) is not a linear function, we can choose three levels of X (say x ₁, x ₂, x ₃) and some z satisfying [E(M | x ₁, z) − E(M | x ₂, z)]∕(x ₁ − x ₂) ≠ [E(M | x ₂, z) − E(M | x ₃, z)]∕(x ₂ − x ₃). Then the following equation from model (13.12) has a unique solution because the coefficient matrix has full rank:

$$\displaystyle\begin{array}{rcl} \left [\begin{array}{cc} E(M\vert x_{1},z) - E(M\vert x_{2},z)&x_{1} - x_{2} \\ E(M\vert x_{2},z) - E(M\vert x_{3},z)&x_{2} - x_{3}\\ \end{array} \right ]\left [\begin{array}{c} b_{1} \\ b_{2} \end{array} \right ]& =& \left [\begin{array}{c} E(Y \vert x_{1},z) - E(Y \vert x_{2},z) \\ E(Y \vert x_{2},z) - E(Y \vert x_{3},z) \end{array} \right ].{}\\ \end{array}$$

Thus the parameters can be identified.

For situation (ii), since E(M | X, Z) is not additive with respect to X and Z, we can find two levels of X (say x ₁, x ₂) and two levels of Z (say z ₁, z ₂) satisfying E(M | x ₁, z ₁) − E(M | x ₂, z ₁) ≠ E(M | x ₁, z ₂) − E(M | x ₂, z ₂). The following equation derived from model (3.4) has a unique solution because the coefficient matrix has full rank:

$$\displaystyle\begin{array}{rcl} \left [\begin{array}{cc} E(M\vert x_{1},z_{1}) - E(M\vert x_{2},z_{1})&x_{1} - x_{2} \\ E(M\vert x_{1},z_{2}) - E(S\vert x_{2},z_{2}) &x_{1} - x_{2}\\ \end{array} \right ]\left [\begin{array}{c} b_{1} \\ b_{2} \end{array} \right ]& =& \left [\begin{array}{c} E(Y \vert x_{1},z_{1}) - E(Y \vert x_{2},z_{1}) \\ E(Y \vert x_{1},z_{2}) - E(Y \vert x_{2},z_{2}) \end{array} \right ].{}\\ \end{array}$$

Thus the parameters can be identified.

For necessity, if E(M | X, Z) = cX +ψ(Z) for some constant c and ψ(⋅ ), then from model (13.12), we have

$$\displaystyle\begin{array}{rcl} E(Y \vert X,Z)& =& b_{0} + b_{1}E(M\vert X,Z) + b_{2}X + E[\phi (U,Z,\varepsilon _{Y })\vert Z] {}\\ & =& b_{0} + (b_{1}c + b_{2})X +\varPhi (Z), {}\\ \end{array}$$

where Φ(Z) = b ₁ ψ(Z) + E[ϕ(U, Z, ɛ _Y ) | Z]. We can easily see that only c, b ₁ c + b ₂ and Φ(Z) can be identified given observed data of (Z, X, M, Y ). b ₁ and b ₂ cannot be identified because (1) E(M | X, Z) is linear with respect to X, and (2) E[ϕ(U, Z, ɛ _Y ) | Z] cannot be identified since U and ɛ _Y are never observed. Thus the parameters in model (13.12) are identifiable only if E(M | X, Z) ≠ cX +ψ(Z).

Appendix 3: Proof for the Equivalence of Different Choices of f(⋅ ) in Eq. (13.15) for the Estimation When the Identifiability Condition in Theorem 1 Holds

We want to show that an arbitrary vector function f(⋅ ) that identifies β via Eq. (13.15) leads to the same estimator as that based on the function f ^∗(⋅ ). For an arbitrary vector function f(⋅ ) = (f ₁(⋅ ), f ₂(⋅ ), ⋯ , f _K (⋅ ))′ (K > 2), we can denote it as

$$\displaystyle\begin{array}{rcl} \mathbf{f}(X)& =& \left [\begin{array}{ccc} f_{1}(1) & f_{1}(2) & f_{1}(3)\\ \vdots & \vdots & \vdots \\ f_{K}(1)&f_{K}(2)&f_{K}(3) \end{array} \right ]\left [\begin{array}{c} \delta (X = 1) \\ \delta (X = 2) \\ \delta (X = 3) \end{array} \right ].{}\end{array}$$

(13.21)

Let Q denote the K × 3 matrix on the right-hand side. Equation (13.15) can be rewritten as G β = H, where G = E[f(X), M f(X), X f(X)] and H = E[Y f(X)]. Then the estimation equation for β is $\widehat{G}\hat{\beta } =\widehat{ H}$. From (13.21), we have

$$\displaystyle\begin{array}{rcl} \widehat{G}& =& \widehat{E}[\mathbf{f}(X),M\mathbf{f}(X),X\mathbf{f}(X)] {}\\ & =& \widehat{E}[Q\mathbf{f}^{{\ast}}(X),MQ\mathbf{f}^{{\ast}}(X),XQ\mathbf{f}^{{\ast}}(X)] {}\\ & =& Q\widehat{E}[\mathbf{f}^{{\ast}}(X),M\mathbf{f}^{{\ast}}(X),X\mathbf{f}^{{\ast}}(X)] {}\\ & =& Q\widehat{G^{{\ast}}}, {}\\ \end{array}$$

where $\widehat{E}(\cdot )$ denotes the sample mean of the corresponding variable. Similarly, we have

$$\displaystyle{\widehat{H} = Q\widehat{H^{{\ast}}}.}$$

Then by the function f(⋅ ), the estimation equation for β is equivalent to

$$\displaystyle\begin{array}{rcl} \widehat{G}\hat{\beta } -\widehat{ H} = Q(\widehat{G^{{\ast}}}\hat{\beta }-\widehat{ H^{{\ast}}}) = 0.& & {}\\ \end{array}$$

Since $\hat{\beta }^{{\ast}}$ satisfies the equation $\widehat{G^{{\ast}}}\hat{\beta }^{{\ast}}-\widehat{ H^{{\ast}}} = 0$, we have that $\hat{\beta }^{{\ast}}$ also satisfies $\widehat{G}\hat{\beta }^{{\ast}}-\widehat{ H} = 0$. Thus we proved $\hat{\beta }=\hat{\beta } ^{{\ast}}$ when Q has full rank, which means that the above equation of $\hat{\beta }$ has a unique solution.

Appendix 4: Proof for Matrix G ^eff in Sect. 13.4.2 Equals E[f ^eff(X)f ^eff(X)′] and Has Full Rank When Non-linearity Condition in Theorem 1 Holds

• (i) We show that G ^eff = E[f ^eff(X)f ^eff(X)′]. It is obvious that

  $$\displaystyle\begin{array}{rcl} E[\mathbf{f}^{\mathrm{eff}}(X)\mathbf{f}^{\mathrm{eff}}(X)']& =& E\left \{\left [\begin{array}{ccc} 1 & E(M\vert X) & X \\ E(M\vert X)& E(M\vert X)^{2} & E(M\vert X)X \\ X &XE(M\vert X)& X^{2}\end{array} \right ]\right \} {}\\ & =& \left [\begin{array}{ccc} 1 & E(M) & E(X) \\ E(M)&E[E(M\vert X)^{2}]&E(XM) \\ E(X) & E(XM) & E(X^{2})\end{array} \right ] = G^{\mathrm{eff}}.{}\\ \end{array}$$

• (ii) We prove that G ^eff has full rank when non-linearity condition in Theorem 1 holds. To prove that G ^eff has full rank, we only need show that det(G ^eff) ≠ 0 when | ρ(X, E(M | X)) |  < 1. We have

  $$\displaystyle\begin{array}{rcl} \mathrm{det}(G^{\mathrm{eff}})& =& \left \vert \begin{array}{ccc} 1 & E(M) & E(X) \\ E(M)&E[E(M\vert X)^{2}]&E(XM) \\ E(X) & E(XM) & E(X^{2})\end{array} \right \vert {}\\ & =& \left \vert \begin{array}{ccc} 1& E(M) & E(X) \\ 0&E[E(M\vert X)^{2}] - [E(M)]^{2} & E(XM) - E(X)E(M) \\ 0& E(XM) - E(X)E(M) & E(X^{2}) - [E(X)]^{2}\end{array} \right \vert.{}\\ \end{array}$$

  Since

  $$\displaystyle{\mathrm{var}[E(M\vert X)] = E[E(M\vert X)^{2}] - [E(M)]^{2},\mathrm{var}(X) = E(X^{2}) - [E(X)]^{2}}$$

  and

  $$\displaystyle{\mathrm{cov}(X,E(M\vert X)) = E[XE(M\vert X)]-E(X)E[E(M\vert X)] = E(XM)-E(X)E(M),}$$

  we have

  $$\displaystyle\begin{array}{rcl} \mathrm{det}(G^{\mathrm{eff}})& =& \left \vert \begin{array}{ccc} 1& E(M) & E(X) \\ 0& \mathrm{var}[E(M\vert X)] &\mathrm{cov}(X,E(M\vert X)) \\ 0&\mathrm{cov}(X,E(M\vert X))& \mathrm{var}(X)\end{array} \right \vert {}\\ & =& \mathrm{var}[E(M\vert X)]\mathrm{var}(X)(1 - [\rho (X,E(M\vert X)]^{2}) > 0, {}\\ \end{array}$$

  since | ρ(X, E(M | X)) |  < 1.