Pricing Options on EU ETS Certificates with a Time-Varying Market Price of Risk Model

Abstract

To price options on emission certificates reduced-form models have proved to be useful. We empirically analyse the performance of the model proposed in Carmona and Hinz [2] and Hinz [8]. As we find evidence for a time-varying market price of risk, we extend the Carmona-Hinz framework by introducing a bivariate pricing model. We show that the extended model is able to extract information on the market price of risk and evaluate its impact on the EUA options.

1 Introduction

The European Union Emissions Trading Scheme (EU ETS) was launched in 2005 and constitutes still the world’s largest carbon market. The EU ETS was set up as a cap-and-trade scheme and split up into three phases, namely Phase I (2005–07) without the possibility to bank unused permits; Phase II (2008–12) in which banking was allowed; and the current Phase III (2013–20) which, compared to the two previous periods, introduced significant changes, such as the abolishment of national allocation plans and the auctioning of permits.

Besides permits, futures and options on permits are being traded. Various authors have discussed the design of the market and the pricing of the permits and the derivatives traded. The fundamental concepts for emission trading and the market mechanism have been reviewed in the paper of Taschini [15], which also provides a literature overview. Equilibrium models for allowance permit markets have been widely used to capture the theoretical properties of emission trading schemes. Examples are the dynamic but deterministic model proposed by Rubin [13] and stochastic equilibrium approaches such as Seifert et al. [14], Wagner [16] and Carmona et al. [3]. These models use optimal stochastic control to investigate the dynamic emission trading in the risk-neutral framework. Carmona et al. [4] derive the permit price formula which can be described as the discounted penalty multiplied by the probability of the excess demand event. Its historical model fit has been evaluated by Grüll and Taschini [6]. Grüll and Kiesel [5] used the formula to analyse the emission permit price drop during the first compliance period. Carmona and Hinz [2] and Hinz [8] propose a reduced-form model which is particular feasible for the calibration of EUA futures and options as it directly models the underlying price process. Both Paolella and Taschini [12] and Benz and Trück [1] provide an econometric analysis for the short-term spot price behavior and the heteroscedastic dynamics of the price returns. For the option pricing, Carmona and Hinz [2] derive a option pricing formula from their reduced-form model for a single trading period. They also discuss the extension of the formula to two trading periods. Hitzemann and Uhrig-Homburg [9, 10] develop an option pricing model for multi-compliance periods by considering a remaining value component in the pricing formula capturing the expected value after a finite number of trading periods.

As emission certificates are traded assets their price paths carry information on the market participant expectations on the development of the fundamental price drivers of the certificates including the regulatory framework. In particular, prices of futures and options of certificates carry forward-looking information which can be extracted by using appropriate valuation models. In this paper we derive such a model by extending the reduced-form pricing model of Carmona and Hinz [2]. Using an extensive data set we extract a time series for the implied market price of risk, which relates to the risk premium the investors attach to the certificates. This requires a calibration of the model to historical price data during varying time periods and with different maturities of futures and options. A crucial step in the calibration procedure is a price transformation of normalized futures prices of permits from a pricing measure to the historical measure. We find that the implied market price of risk possesses stochastic characteristics. Therefore, we extend the existing reduced-form model by modeling the dynamics of the market price of risk as an Ornstein-Uhlenbeck process and show that the extended model captures the appropriate properties of the market. The market price of risk is an implied value related to the permit prices, this requires an extension of the univariate permit pricing model to a bivariate one. In this context, the standard Kalman filter algorithm is considered to be an effective way to calibrate to the historical prices. We apply this methodology and estimate the implied risk premia. Once the risk premia have been determined, EUA option prices can be derived to fit the bivariate model setting, which helps to improve the accuracy of the pricing.

This paper is organized as follows. In Sect. 2 we introduce the basic reduced-form model based on a risk-neutral framework. We calibrate the model with an extended data series and compare the calibration results. In Sect. 3 an extended bivariate pricing model will be introduced in order to capture the market information of the risk premia. We demonstrate how to calibrate the extended model by applying the standard Kalman filter algorithm, we present the estimation results of this procedure and discuss the model fit. In Sect. 4 we evaluate the option pricing performance by taking into account the calibration results of the bivariate model. Section 5 concludes.

2 Univariate EUA Pricing Model and Parameter Estimation

The basic reduced-form model based on a risk-neutral framework was introduced by Carmona and Hinz [2]. Here, the aggregated normalised emissions are modelled directly and it can be shown that the emission certificate futures process solves a stochastic differential equation. In this section we give a brief introduction to the model and discuss the quality of the model calibration.

2.1 Univariate Model

We consider an emission trading scheme with a single trading phase with horizon [0, T]. The price evolution of emission permits is assumed to be adapted stochastic processes on a filtered probability space $(\varOmega , \mathscr {F}, (\mathscr {F}_t)_{t\in [0, T]}, \mathbb {P})$ with an equivalent risk-neutral measure $\mathbb {Q} \sim \mathbb {P}$. Based on the assumption of a market compliance at time T the price has only two possible outcomes, namely zero or the penalty level. The argument is as follows. If there are sufficient emission allowances in the market to cover the total emissions at compliance time, surplus allowances will become worthless. Otherwise, for undersupplied permits the price will increase to the penalty level.

We introduce the reduced-form model of Carmona and Hinz [2]. Here the normalized futures price process is a martingale under $\mathbb {Q}$ given by

$$\begin{aligned} a_t=\mathbb {E}^{\mathbb {Q}}[1_{\{\varGamma _T\ge 1\}}| \mathscr {F}_t], \quad t\in [0, T]. \end{aligned}$$

(1)

The process $(\varGamma _t)_{t\in [0, T]}$ denotes the aggregated normalized emission, and is assumed to follow a lognormal process given by

$$\begin{aligned} \varGamma _t=\varGamma _0 e^{\int _0^t \sigma _s d\widetilde{W}_s -\frac{1}{2}\int _0^t \sigma _s^2 ds}, \quad \varGamma _0\in (0, \infty ), \end{aligned}$$

where $\sigma _t$ stands for the volatility of the emission pollution rate. $t\hookrightarrow \sigma _t$ is a deterministic function which is continuous and square-integrable. $(\widetilde{W}_t)_{t\in [0, T]}$ is a Brownian motion with respect to $\mathbb {Q}$. Carmona and Hinz [2] prove that $a_t$ solves the stochastic differential equation

$$\begin{aligned} da_t=\varPhi '(\varPhi ^{-1}(a_t))\sqrt{z_t}d\widetilde{W}_t, \end{aligned}$$

(2)

with the function $t\hookrightarrow z_t$, $t\in (0, T)$, given by

$$\begin{aligned} z_t=\frac{\sigma _t^2}{\int _t^T \sigma _u^2du}. \end{aligned}$$

(3)

In order to calibrate the model, Carmona and Hinz [2] suggest to use the function

$$\begin{aligned} z_t=\beta (T-t)^{-\alpha }, \end{aligned}$$

with $\alpha \in \mathbb {R}$ and $\beta \in (0, \infty )$, so one has

$$\begin{aligned} da_t=\varPhi '(\varPhi (a_t))\sqrt{\beta (T-t)^{-\alpha }}d\widetilde{W}_t. \end{aligned}$$

(4)

To estimate the parameters one has to determine the distribution of the price variable. For this purpose one considers the price transformation process $\xi _t$ defined by $a_t=\varPhi (\xi _t)$, where $\varPhi$ denotes the cumulative distribution function of the standard normal distribution. By applying Itô’s formula one has

$$\begin{aligned} d\xi _t = \displaystyle \left( \frac{1}{2}z_t\xi _t+\sqrt{z_t}h\right) dt+\sqrt{z_t}dW_t, \end{aligned}$$

(5)

where $W_t$ denotes the Brownian motion under the objective measure $\mathbb {P}$ and h is the market price of risk which is assumed to be constant. Moreover, it can be shown that $\xi _t$ is conditional Gaussian with mean $\mu _t$ and variance $\sigma _t^2$ so that the log-likelihood can be calculated and Maximum-likelihood estimation can be applied to find the model parameters.

2.2 Estimation

We calibrate the model to different emission trading periods during the first and second EU ETS trading phases. We consider the daily prices of the EUA futures with maturities in December from 2005 to 2012. Their historical price series are shown in Fig. 1.

Fig. 1

Historical prices of the EUA futures with maturities in December from 2005 to 2012

The price transformation $\xi _t$ is conditional Gaussian with its mean $\mu _t$ and variance $\sigma _t^2$. We consider the daily historical observations of the EUA futures at time $t_1, t_2, \ldots , t_n$. Their corresponding price transformations can be determined using the definition $a_t=\varPhi (\xi _t)$. Thus the parameters $\alpha , \beta , h$ can be estimated by maximizing the log-likelihood function given by

$$\begin{aligned} L_{\xi _{t_i},\ldots ,\xi _{t_n}}(h, \alpha , \beta )=\sum ^n_{i=1}\left( -\frac{(\xi _{t_i}-\mu _i(h, \alpha , \beta ))^2}{2\sigma ^2_i(\alpha , \beta )}-\ln \left( \sqrt{2\pi \sigma ^2_i (\alpha , \beta )}\right) \right) . \end{aligned}$$

(6)

Under the model assumptions the residuals

$$\begin{aligned} w_i=\frac{\xi _{t_i}-\mu _i(h, \alpha , \beta )}{\sqrt{\sigma ^2_i(\alpha , \beta )}}, \quad i=1,\ldots ,n, \end{aligned}$$

(7)

must be a series of independent standard normal random variables. So standard statistical analysis can be applied to test the quality of the model fit. We show our estimation results in Table 1. The horizons of the price data are two years, starting from the first trading day in January of the previous trading year to the last trading day in December of the next year.

Comparing the estimation values in Table 1, the instability of the parameter values in each cell for different time periods can be observed. Note the value for the market price of risk changes its sign during the first and second trading phase. This implies the inappropriateness of the assumption for a constant market price of risk. The fourth value in each cell is the negative of LLF. Note the -LLF are much lower after the first trading phase because the price collapse during 2006 to 2007 affects the data partially.

From Figs. 2, 3, 4, 5 and 6 we display the time series of the residuals $w_i$, their empirical auto-correlations, empirical partial auto-correlations and quantile-quantile-plots. We choose EUA futures with maturity in December 2007 (EUA 07) and EUA futures with maturity in December 2012 (EUA 12) as examples.

The time series $w_i$ show an effect of volatility clustering. This is confirmed by significant values to high lags in the sample autocorrelation and sample partial autocorrelation. Also the Q-Q plots, especially for the first trading phase, indicate heavy tails and a non-Gaussian behavior. A formal analysis with an application of Jarque-Bera test rejects the hypothesis that the data set is generated from normally distributed random variables. In order to improve the model fit we extend the model by introduction of a dynamic market price of risk in Sect. 3.

Table 1 Parameter estimate results

Fig. 2

Statistical analysis of EUA 07, time period 05–06 and 06–07

Fig. 3

Statistical analysis of EUA 12, time period 05–06 and 06–07

Fig. 4

Statistical analysis of EUA 12, time period 07–08 and 08–09

Fig. 5

Statistical analysis of EUA 12, time period 09–10 and 10–11

Fig. 6

Statistical analysis of EUA 12, time period 11–12

3 Bivariate Pricing Model for EUA

The evidence in the previous section shows that the market price of risk is actually time varying rather than constant. In order to illustrate the dynamic property of the market price of risk we consider a bivariate permit pricing model in this section.

3.1 Model Description

We model the market price of risk as an Ornstein-Uhlenbeck process as its value can be either positive or negative and denote it by $\lambda _t$. Recall the equation for the normalized price process under the risk-neutral measure $\mathbb {Q}$ given by (2). According to Girsanov’s theorem, the bivariate pricing model under the objective measure $\mathbb {P}$ is given by

$$\begin{aligned} da_t= & {} \displaystyle \varPhi '(\varPhi ^{-1}(a_t))\sqrt{z_t}(\lambda _tdt+dW_t^1),\\ d\lambda _t= & {} \theta (\bar{\lambda }-\lambda _t)dt+\sigma _\lambda dW_t^2,\\ dW_t^1dW_t^2= & {} \rho dt, \end{aligned}$$

where $W_t^1$ and $W_t^2$ are two one-dimensional Brownian motions with correlation coefficient $\rho$. Note that under the model assumptions, the filtration $(\mathscr {F}_t)$ in the probability space must be assumed to be generated by the bivariate Brownian motion.

The use of Girsanov’s theorem in the bivariate model requires the condition that the process $Z_t$ given by

$$\begin{aligned} Z_t=\exp \Big (\int _0^t \lambda _s dW_s-\frac{1}{2}\int _0^t \lambda _s^2 ds\Big ) \end{aligned}$$

(8)

is a martingale. A sufficient condition for (8) is Novikov’s condition:

$$\begin{aligned} \mathbb {E}\Big [\exp \Big (\frac{1}{2}\int _0^T\lambda _s^2 ds\Big )\Big ]<\infty . \end{aligned}$$

(9)

Under our model assumptions, this condition is always satisfied.¹

To calibrate the model we use the transformed price process to avoid complex numerical calculations in the calibration procedure. The bivariate model can be reformulated as

$$\begin{aligned} d\xi _t= & {} \displaystyle \left( \frac{1}{2}z_t\xi _t+\sqrt{z_t}\lambda _t\right) dt+\sqrt{z_t}dW_t^1,\end{aligned}$$

(10)

$$\begin{aligned} d\lambda _t= & {} \theta (\bar{\lambda }-\lambda _t)dt+\sigma _\lambda dW_t^2, \end{aligned}$$

(11)

$$\begin{aligned} dW_t^1dW_t^2= & {} \rho dt. \end{aligned}$$

(12)

In (11), $\bar{\lambda }$ represents the long-term mean value. $\theta$ denotes the rate with which the shocks dissipate and the variable reverts towards the mean. $\sigma _\lambda$ is the volatility of the market price of risk. According to Carmona and Hinz [2], the price transformation is conditional Gaussian and its SDE can be solved explicitly.

3.2 Calibration to Historical Data

We consider the discretization of the model (10)–(12). By assuming the constant volatility terms in the time interval $[t_{k-1}, t_{k}]$, the model equations can be discretized under Euler’s scheme given by

$$\begin{aligned} \xi _{t_k}&= \sqrt{z_{t_{k-1}}}\triangle t\lambda _{t_{k-1}}+\left( 1+\frac{1}{2}z_{t_{k-1}}\right) \xi _{t_{k-1}}+\sqrt{z_{t_{k-1}}\triangle t}\mathscr {E}^1_{t_{k}},\end{aligned}$$

(13)

$$\begin{aligned} \lambda _{t_k}&= (1-\theta \triangle t)\lambda _{t_{k-1}}+\theta \bar{\lambda }\triangle t+\sigma _\lambda \sqrt{\triangle t}\mathscr {E}^2_{t_k},\end{aligned}$$

(14)

$$\begin{aligned} Cov(\mathscr {E}_{t_k}^1, \mathscr {E}_{t_k}^2)&= \rho , \end{aligned}$$

(15)

where $\triangle t = t_k-(t_{k-1})$, namely the time interval, and $\mathscr {E}_{t_k}^1$, $\mathscr {E}_{t_k}^2 \sim \mathscr {N}(0, 1)$. $z_{t_k}$ can be modeled by using the function $\beta (T-t_k)^{-\alpha }$. The model parameter-set is therefore $\psi =[\theta , \bar{\lambda }, \sigma _\lambda , \rho , \alpha , \beta ]$.

As $\lambda _{t_k}$ is a hidden state variable related to the price transformation, and only values of $\xi _{t_k}$ at time points $t_1, t_2, \ldots , t_n$ can be determined from the market observations, the market price of risk series can be estimated by applying the Kalman filter algorithm. We have chosen to use the transformation process instead of the normalized price $a_{t_k}$. Because of the linear form of Eqs. (13) and (14) the standard Kalman filter algorithm is considered to be an efficient method for the model calibration. A detailed procedure to apply the standard Kalman filter can be found in [7]. To apply the Kalman filter model Eqs. (13)–(15) must be put into the state space representation to fit the model framework. The measurement equation links the unobservable state to observations. It can be derived from (13) and (14). After some manipulations, the equations of the state space form for the model can be rewritten² as

$$\begin{aligned} S_{t_k} = \sqrt{\beta (T-t_k)^{-\alpha }}\triangle t\lambda _{t_k}+\left( 1+\frac{1}{2}(\beta (T-t_k)^{-\alpha })\right) \xi _{t_k}+\sqrt{\beta (T-t_k)^{-\alpha }\triangle t}\bar{\mathscr {E}}_{t_k}^1, \end{aligned}$$

(16)

and

$$\begin{aligned} \lambda _{t_k}= & {} \left[ \theta \bar{\lambda }\triangle t -\frac{\sigma _\lambda \rho }{\sqrt{\beta (T-t_k)^{-\alpha }}}\left( \left( 1+\frac{1}{2}(\beta (T-t_k)^{-\alpha })\right) \xi _{t_{k-1}}-\xi _{t_k}\right) \right] \nonumber \\&+(1-\theta \triangle t-\sigma _\lambda \rho \triangle t)\lambda _{t_{k-1}}+\sigma _\lambda \sqrt{(1-\rho ^2)\triangle t}\bar{\mathscr {E}}_{t_k}^2, \end{aligned}$$

(17)

where $\bar{\mathscr {E}}_{t_k}^1$ and $\bar{\mathscr {E}}_{t_k}^2$ are independent, standard normally distributed random variables.

For the estimation of the parameter vector $\psi =[\theta , \bar{\lambda }, \sigma _\lambda , \rho , \alpha , \beta ]$ consider the variable $\xi _{t_k}$. In each iteration of the filtering procedure, the conditional mean $\mathbb {E}[\xi _{t_k} | \xi _{t_1},\ldots , \xi _{t_{k-1}}]$ and the conditional variance $Var(\xi _{t_k} | \xi _{t_1},\ldots , \xi _{t_{k-1}})$ can be calculated. We denote mean and variance by $\mu _{t_k}(\psi )$ and $\varSigma _{t_k}(\psi )$, respectively. The joint probability density function of the observations is denoted by $f(\xi _{t_{1:n}} | \psi )$ and is given by

$$\begin{aligned} f(\xi _{t_{1:n}} | \psi )=\prod _{k=1}^n\frac{1}{\sqrt{2\pi \varSigma _{t_k}(\psi )}}\exp \left( -\frac{(\xi _{t_k}-\mu _{t_k}(\psi ))^2}{2\varSigma _{t_k}(\psi )}\right) , \end{aligned}$$

where $\xi _{t_{1:n}}$ summarize the observations from $\xi _{t_1}$ to $\xi _{t_n}$. Its corresponding log-likelihood function is given by

$$\begin{aligned} \mathscr {L}_{obs}(\psi | \xi _{t_{1:n}})=-\frac{n}{2}\log 2\pi -\frac{1}{2}\sum _{k=1}^n\log \varSigma _{t_k}(\psi )-\frac{1}{2}\sum _{k=1}^n\frac{(\xi _{t_k}-\mu _{t_k}(\psi ))^2}{\varSigma _{t_k}(\psi )}. \end{aligned}$$

(18)

The estimation results, their standard errors, t-tests and p-values can be found in Table 2. Figure 7 shows the estimation results of the market price of risk, compared with the price transformation and the historical futures price. In Fig. 8, a negative correlation between the price transformation and the market price of risk can be seen. The market price of risk is the return in excess of the risk-free rate that the market wants as compensation for taking the risk.³ It is a measure of the extra required rate of return, or say, a risk premium, that investors need for taking the risk. The more risky an investment is, the higher the additional expected rate of return should be. So in order to achieve a higher required rate of return, the asset must be discounted and thus will be sold at a lower price. Figure 8 reveals this inverse relationship.

Table 2 Test of model parameters at significance level 5 %, sample size 1536

Fig. 7

MPR, futures price and price transformation from Jan. 2007 to Dec. 2012

Fig. 8

Negative correlation of MPR and price transformation

Moreover, we use the mean pricing errors (MPE) and the root mean squared errors (RMSE) given by

$$\begin{aligned} MPE= & {} \frac{1}{N}\sum ^N_{t_i=1}(\bar{\xi }_{t_i, \tau }-\xi _{t_i, \tau }),\\ RMSE= & {} \left( \frac{1}{N}\sum ^N_{t_i=1}(\bar{\xi }_{t_i, \tau }-\xi _{t_i, \tau })^2\right) ^{\frac{1}{2}}, \end{aligned}$$

respectively, to assess the quality of model fit. Here N denotes the number of observations, $\bar{\xi }_{t_i, \tau }$ is the estimated price to maturity $\tau$, and $\xi _{t_i, \tau }$ is the observed price. Their values can be seen in Table 3. The absolute values of MPE and RMSE increase with time but still remain very low even 9 months before the maturity. Therefore, the conclusion is that the model is able to reproduce the price dynamics.

Table 3 Performance of MPE and RMSE with 2000 observations

In Fig. 9 we show the standard statistical test results of the residuals by taking into account the dynamic market price of risk. Comparing with the results from Figs. 2, 3, 4, 5 and 6, the time series of the residuals is relative stable with smaller variance. The sample auto-correlations and sample partial auto-correlations reveal very weak linear dependence of the variables at different time points. Also, the Q-Q plot indicates a better fit of a Gaussian distribution.

Fig. 9

Statistical tests for the residuals in trading phase 2

4 Option Pricing and Market Forward Looking Information

A general pricing formula of a European call is given by

$$\begin{aligned} C_t=e^{-\int _t^\tau r_sds}\mathbb {E}^{\mathbb {Q}}[(A_\tau -K)^+|\mathscr {F}_t], \end{aligned}$$

where $\{r_s\}_{s\in [0, T]}$ stands for a deterministic rate, $A_t$ denotes the futures price, $K\ge 0$ is the strike price, and $\tau \in [0, T]$ is the maturity. The normalized price process $a_t$ is given by $a_t=A_t/P$, where P denotes the penalty for each ton of exceeding emissions, and therefore we have $A_t=P\varPhi (\xi _t)$. A call option price formula written on EUA has been derived by Carmona and Hinz [2] under the assumption of a constant market price of risk. Under the assumption of a dynamic market price of risk, the option price formula is coherent with the formula in [2] given by

$$\begin{aligned} C_t=e^{-\int _t^\tau r_sds}\int _\mathbb {R}(P\varPhi (x)-K)^+\varphi (\mu _{t, \tau }, \sigma ^2_{t, \tau })dx, \end{aligned}$$

where $\varphi$ stands for the density function of a standard normal distribution. Here $\mu _{t, \tau }$ and $\sigma ^2_{t, \tau }$ are the parameters of the distribution of $\xi _t$, which is conditional Gaussian. Under the risk neutral measure $\mathbb {Q}$, $\mu _{t, \tau }$ and $\sigma ^2_{t, \tau }$ are given by

$$\begin{aligned} \mu _{t, \tau } = e^{\frac{1}{2}\int _t^\tau z_s ds}\xi _t, \qquad \sigma ^2_{t, \tau } = \int _t^\tau z_s e^{\int _s^\tau z_u du}ds. \end{aligned}$$

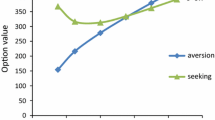
In the following example, the penalty level is $P=100$, the initial time $t=0$ starts in April 2005. EUA futures has maturity T on the last trading day in 2012. The European calls written on EUA futures with a strike at $K=15$ and maturity T will be considered under a constant interest rate at $r=0.05$. Figure 10 shows the call option prices and the futures prices. The red curve stands for the option prices under dynamic MPR while the green curve stands for the option prices under constant MPR.

Fig. 10

Futures price and call option prices with $K=15$ from 2005 to 2012

To measure the impact of the dynamic market price of risk on the EUA option for different strikes we calculate the option price in the univariate and bivariate model setting respectively. Durations from 1, 3, 6 and 12 months to maturity are chosen for calls written on EUA 2012. The results are plotted in Fig. 11. The red curve stands for the option prices evaluated by the bivariate model and the blue curve by the univariate model. The green line is the corresponding futures price at the given time. In most cases, one is interested in the option prices near the underlying price. According to the figure, the option prices in different model settings coincide except for a interval around the corresponding futures. In a short time before the maturity of EUA 2012, Fig. 11 shows a price overestimation by the constant MPR. This result is consistent with the result shown in Fig. 10, where we take $K=15$ as a sample path.

Fig. 11

Call option prices comparison for durations of 1, 3, 6, 12 months on EUA 2012 for different strikes

Moreover, one notes that the call price process with constant MPR develops below the call process with dynamic MPR in the first trading phase before 2008 and then increases slowly and moves to the upside of the call process with dynamic MPR during the second trading phase, before both processes vanish to the maturity because of lower underlying prices. The reason for the price underestimation before 2008 and overestimation thereafter can be explained as the assumption of a constant MPR in the whole trading periods and thus causes a neglect on the information of the market participants. Due to the regulatory framework of the carbon market, certificates carry information on the market participant expectations on the development of the fundamental price drivers. Since the implied risk premia increase with time and exceed their ’average’ level in 2008, asset price must be discounted to compensate the higher risk. By using appropriate valuation models, this risk premia and the forward-looking information carried by prices of futures and options of certificates can be extracted.

5 Conclusion

We extract forward-looking information in the EU ETS by applying an extended pricing model of EUA futures and analyzing its impact on option prices. We find that the implied risk premium is time-varying and has to be modeled by a stochastic process. Using the information given by the risk premium we show that the option prices during the first and second trading phases are underestimated and overestimated, respectively. The reason for the pricing deviation is caused by the assumption of a constant market price of risk which rigidifies the market participant expectations on the development of price drivers. The over- and underestimated prices are mostly concentrated in the interval including the corresponding futures, which is the area where the price most likely will evolve in the future. Although there is not a closed form for the option pricing formula, a simple numerical approach can be used to determine the price.

Appendices

Appendix 1

In order to show the condition in (8), it is sufficient to prove the Novikov’s condition given by

$$\begin{aligned} \mathbb {E}\Big [\exp \Big (\frac{1}{2}\int _0^T\lambda _s^2 ds\Big )\Big ]<\infty . \end{aligned}$$

In the bivariate EUA pricing model, where $\lambda _t$ follows a Ornstein-Uhlenbeck-Process given by

$$\begin{aligned} \lambda _t=\theta (\bar{\lambda }-\lambda _t)dt+\sigma _\lambda dWt, \end{aligned}$$

this condition is always satisfied.

Proof

We first show that there exists a constant $\varepsilon >0$ such that for any $S\in [0, T]$, we have

$$\begin{aligned} \mathbb {E}\Big [\exp \Big (\frac{1}{2}\int _S^{S+\varepsilon }\lambda _t^2 dt\Big )\Big ]<\infty . \end{aligned}$$

(19)

To show (19) we consider the term in the expectation notation. By applying Jensen’s inequality we have

$$\begin{aligned}&\exp \Big (\frac{1}{2}\int _S^{S+\varepsilon }\lambda _t^2 dt\Big )=\exp \Big (\int _S^{S+\varepsilon }\frac{1}{\varepsilon }\frac{\varepsilon }{2}\lambda _t^2 dt\Big )\\= & {} \exp \Big (\frac{1}{\varepsilon }\int _S^{S+\varepsilon }\frac{\varepsilon }{2}\lambda _t^2 dt\Big )\le \frac{1}{\varepsilon }\int _S^{S+\varepsilon }\exp \Big (\frac{\varepsilon }{2}\lambda _t^2\Big )dt. \end{aligned}$$

By applying Fubini’s theorem (19) becomes

$$\begin{aligned} \frac{1}{\varepsilon }\int _S^{S+\varepsilon }\mathbb {E}\Big [\exp \Big (\frac{\varepsilon }{2}\lambda _t^2\Big )\Big ]dt. \end{aligned}$$

(20)

The process $\lambda _t$ is a Gaussian process with mean and variance given by

$$\begin{aligned} \mathbb {E}[\lambda _t]=\mu _t=\lambda _0 e^{-\theta t}+\bar{\lambda }(1-e^{-\theta t}),\\ \text {Var}(\lambda _t)=\sigma _t^2=\frac{\sigma _\lambda ^2}{2\theta }(1-e^{-2\theta t}). \end{aligned}$$

We have $\lambda _t\sim \mathscr {N}(\mu _t, \sigma _t^2)$. Now let Z be a standard normal-distributed random variable $Z\sim \mathscr {N}(0, 1)$. So in (20) we have

$$\begin{aligned} \mathbb {E}\Big [\exp \Big (\frac{\varepsilon }{2}\lambda _t^2\Big )\Big ]= & {} \mathbb {E}\Big [\exp \Big (\frac{\varepsilon }{2}(\mu _t+\sigma _t Z)^2\Big )\Big ]\\= & {} \mathbb {E}\Big [\exp \Big (\frac{\varepsilon \mu _t^2}{2}+\varepsilon \mu _t\sigma _t Z+\frac{\varepsilon \sigma _t^2Z^2}{2}\Big )\Big ]\\= & {} \int _\mathbb {R}\exp \Big (\frac{\varepsilon \mu _t^2}{2}+\varepsilon \mu _t\sigma _t x+\frac{\varepsilon \sigma _t^2x^2}{2}\Big )\frac{1}{\sqrt{2\pi }}\exp \Big (-\frac{x^2}{2}\Big )dx\\= & {} \exp \Big (\frac{\varepsilon \mu _t^2}{2}\Big )\int _\mathbb {R}\frac{1}{\sqrt{2\pi }}\exp \Big (-\frac{1-\varepsilon \sigma _t^2}{2}x^2+\varepsilon \mu _t\sigma _t x\Big )dx. \end{aligned}$$

To calculate the integration term above, let $a_t=1-\varepsilon \sigma _t^2$ and $b_t=\varepsilon \mu _t\sigma _t$, and make the integral-substitution. Then we have

$$\begin{aligned}&\int _\mathbb {R}\frac{1}{\sqrt{2\pi }}\exp \Big (-\frac{1-\varepsilon \sigma _t^2}{2}x^2+\varepsilon \mu _t\sigma _t x\Big )dx\\= & {} \int _\mathbb {R}\frac{1}{\sqrt{2\pi }}\exp \Big (-\frac{1}{2}(a_tx^2-2b_t x)\Big )dx\\= & {} \int _\mathbb {R}\frac{1}{\sqrt{2\pi }}\exp \Big (-\frac{1}{2}\Big (y^2-2b_t\frac{1}{\sqrt{a_t}}y\Big )\Big )\frac{1}{\sqrt{a_t}}dy\\= & {} \frac{1}{\sqrt{a_t}}\int _\mathbb {R}\frac{1}{\sqrt{2\pi }}\exp \Big (-\frac{1}{2}\Big (y^2-\frac{2b_t}{\sqrt{a_t}}y+\Big (\frac{b_t}{\sqrt{a_t}}\Big )^2 -\Big (\frac{b_t}{\sqrt{a_t}}\Big )^2\Big )\Big )dy\\= & {} \frac{1}{\sqrt{a_t}}\exp \Big (\frac{b_t^2}{2a_t}\Big )\int _\mathbb {R}\frac{1}{\sqrt{2\pi }}\exp \Big (-\frac{(y-\frac{2b_t}{\sqrt{a_t}})^2}{2}\Big )dy\\= & {} \frac{1}{\sqrt{a_t}}\exp \Big (\frac{b_t^2}{2a_t}\Big ). \end{aligned}$$

According to the assumptions $a_t=1-\varepsilon \sigma _t^2$ is positive and the expectation is convergent for a small $\varepsilon$ and its value is

$$\begin{aligned} \mathbb {E}\Big [\exp \Big (\frac{\varepsilon }{2}\lambda _t^2\Big )\Big ]= & {} \frac{1}{\sqrt{a_t}}\exp \Big (\frac{\varepsilon \mu _t^2}{2}\Big )\exp \Big (\frac{b_t^2}{2a_t}\Big )\\= & {} \frac{1}{\sqrt{1-\varepsilon \sigma _t^2}}\exp \Big (\frac{\varepsilon \mu _t^2}{2}\Big )\exp \Big (\frac{\varepsilon ^2\mu _t^2\sigma _t^2}{2-2\varepsilon \sigma _t^2}\Big ). \end{aligned}$$

Thus the integral in (20) is finite and the exponential term in (19) is integrable.

In order to show $Z_t$ is a martingale we first consider that $Z_t$ is a local martingale, hence it is a supermartingale. Therefore, $Z_t$ is a martingale if and only if the condition $\mathbb {E}[Z_t]=1$, $\forall t\in [0, T]$, is satisfied. This martingale property can be shown by induction. Suppose $\mathbb {E}[Z_0]=1$ which is trivial and $\mathbb {E}[Z_t]=1$ for $t\in [0, S]$ for $S<T$. Let now $t\in [S, S+\varepsilon ]$ and set

$$\begin{aligned} Z_S^t=\exp \Big (\int _S^t \lambda _s dW_s-\frac{1}{2}\int _S^t \lambda _s^2 ds\Big ). \end{aligned}$$

According to Novikov condition and (19), $Z_S^t$ is a martingale. Then we have

$$\begin{aligned} \mathbb {E}[Z_t]=\mathbb {E}[Z_S Z_S^t]=\mathbb {E}[\mathbb {E}[Z_S Z_S^t]|\mathscr {F}_S]=\mathbb {E}[Z_S\mathbb {E}[Z_S^t|\mathscr {F}_S]]=\mathbb {E}[Z_S Z_S^S]=\mathbb {E}[Z_S], \end{aligned}$$

since

$$\begin{aligned} Z_S^S=\exp \Big (\int _S^S \lambda _s dW_s-\frac{1}{2}\int _S^S \lambda _s^2 ds\Big )=\exp (0)=1. \end{aligned}$$

It follows

$$\begin{aligned} \mathbb {E}[Z_t]=\mathbb {E}[Z_S]=1 \quad \text {for } t\in [S, S+\varepsilon ]. \end{aligned}$$

Then we have $\mathbb {E}[Z_t]=1$ for $t\in [0, S+\varepsilon ]$. Repeat this induction for $\frac{T-S}{\varepsilon }$ times we have $\mathbb {E}[Z_t]=1$ for $t\in [0, T]$, which implies $Z_t$ defined in (8) is a martingale. $\square$

Appendix 2

The bivariate EUA pricing model can be described as follows:

$$\begin{aligned} \xi _{t_k}= & {} \sqrt{z_{t_{k-1}}}\triangle t\lambda _{t_{k-1}}+\left( 1+\frac{1}{2}z_{t_{k-1}}\right) \xi _{t_{k-1}}+\sqrt{z_{t_{k-1}}\triangle t}\mathscr {E}_{t_k}^1,\\ \lambda _{t_k}= & {} (1-\theta \triangle t)\lambda _{t_{k-1}}+\theta \bar{\lambda }\triangle t+\sigma _\lambda \sqrt{\triangle t}\mathscr {E}_{t_k}^2,\\ Cov(\mathscr {E}_{t_k}^1, \mathscr {E}_{t_k}^2)= & {} \rho , \end{aligned}$$

where $\mathscr {E}_{t_k}^1$ and $\mathscr {E}_{t_k}^2$ are both random variables of the standard normal distribution. We want to put the model into the state space form. Price transformation depends on the current level of the market price of risk, which is an unobservable variable and therefore must be modeled in the equation of $\lambda _{t_k}$. We first let

$$\begin{aligned} \mathscr {E}_{t_k}^1 = \bar{\mathscr {E}}_{t_k}^1, \qquad \mathscr {E}_{t_k}^2 = \sqrt{1-\rho ^2} \bar{\mathscr {E}_{t_k}^2}+\rho \bar{\mathscr {E}_{t_k}^1}, \end{aligned}$$

where $\bar{\mathscr {E}}_{t_k}^1$ and $\bar{\mathscr {E}}_{t_k}^2$ are both random variables of the standard normal distribution as well. This fact can be easily seen since we have

$$\begin{aligned} Cov(\bar{\mathscr {E}}_{t_k}^1, \bar{\mathscr {E}}_{t_k}^2)= Cov\left( \mathscr {E}_{t_k}^1, \frac{\mathscr {E}_{t_k}^2-\rho \mathscr {E}_{t_k}^1}{\sqrt{1-\rho ^2}}\right) =Cov\left( \mathscr {E}_{t_k}^1, \frac{\mathscr {E}_{t-k}^2}{\sqrt{1-\rho ^2}}\right) \,+\,Cov\left( \mathscr {E}_{t_k}^1, -\frac{\rho \mathscr {E}_{t_k}^1}{\sqrt{1-\rho ^2}}\right) =0. \end{aligned}$$

Note that

$$\begin{aligned} \sqrt{z_{t_{k-1}}}\triangle t\lambda _{t_{k-1}}+\left( 1+\frac{1}{2}z_{t_{k-1}}\right) \xi _{t_{k-1}}+\sqrt{z_{t_{k-1}}\triangle t}\mathscr {E}_{t_k}^1-\xi _{t_k}=0. \end{aligned}$$

Multiplying $-\sigma _\lambda \rho (z_{t_{k-1}})^{-\frac{1}{2}}$ at the both sides of the equation and sum it to the equation of $\lambda _{t_k}$, it follows that

$$\begin{aligned} \lambda _{t_k}= & {} (1-\theta \triangle t)\lambda _{t_{k-1}}-\sigma _\lambda \rho \triangle t\lambda _{t_{k-1}}+\theta \bar{\lambda }\triangle t,\\&-\frac{\sigma _\lambda \rho }{\sqrt{z_{t_{k-1}}}}\left( \left( 1+\frac{1}{2}z_{t_{k-1}}\right) \xi _{t_{k-1}}-\xi _{t_k}\right) +\sigma _\lambda \sqrt{\triangle t}\mathscr {E}_{t_k}^2-\sigma _\lambda \sqrt{\triangle t}\rho \mathscr {E}_{t_k}^1\\= & {} (1-\theta \triangle t-\sigma _\lambda \rho \triangle t)\lambda _{t_{k-1}}+\left[ \theta \bar{\lambda }\triangle t -\frac{\sigma _\lambda \rho }{\sqrt{z_{t_{k-1}}}}\left( \left( 1+\frac{1}{2}z_{t_{k-1}}\right) \xi _{t_{k-1}}-\xi _{t_k}\right) \right] \\&+\,\sigma _\lambda \sqrt{\triangle t}\sqrt{1-\rho ^2}\mathscr {E}_{t_k}^2. \end{aligned}$$

This is the transition equation in the state space form, and the measurement equation would be

$$\begin{aligned} S_{t_k} = \xi _{t_{k+1}} = \sqrt{z_{t_k}}\triangle t\lambda _{t_k}+\left( 1+\frac{1}{2}z_{t_k}\right) \xi _{t_k}+\sqrt{z_{t_k}\triangle t}\mathscr {E}_{t_k}^1. \end{aligned}$$