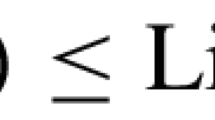Ballistic Transport in Periodic and Random Media

Abstract

We prove ballistic transport of all orders, that is, $\Vert x^m\mathrm{e} ^{-\mathrm{i} tH}\psi \Vert \asymp t^m$, for the following models: the adjacency matrix on $\mathbb {Z}^d$, the Laplace operator on $\mathbb {R}^d$, periodic Schrödinger operators on $\mathbb {R}^d$, and discrete periodic Schrödinger operators on periodic graphs. In all cases we give the exact expression of the limit of $\Vert x^m\mathrm{e} ^{-\mathrm{i} tH}\psi \Vert /t^m$ as $t\to +\infty$. We then move to universal covers of finite graphs (these are infinite trees) and prove ballistic transport in mean when the potential is lifted naturally, giving a periodic model, and when the tree is endowed with random i.i.d. potential, giving an Anderson model. The limiting distributions are then discussed, enriching the transport theory. Some general upper bounds are detailed in the appendix.

Dedicated to the memory of our friend Sergey Naboko

Appendix A: Upper Bounds and Derivatives

Here we first prove that the m-moments grow at most like $t^m$. This already appeared in various forms: for continuous Schrödinger operators see [27] for $m=1,2$; for discrete Schrödinger operators, upper bounds can be deduced from [1, Appendix B] for general moments but $\psi =\delta _x$. Using the upper bounds, we then give rigorous proofs of the moment derivative formulas (A.11) and (A.22).

We start with some general remarks on lower bounds.

1.1 A.1 Lower Bounds

On $L^2(X)$, if $x_0\in X$ is fixed and $\lvert x\rvert := d(x,x_0)$, then we have

$$\displaystyle \begin{aligned} {} \Vert\lvert x\rvert^j\phi\Vert^2=\langle\phi,\lvert x\rvert^{2j}\phi\rangle=\int_X\lvert x\rvert^{2j}|\phi|{}^2 &\leq\Bigl(\int_X\lvert x\rvert^{2m}\lvert\phi\rvert^2\Bigr)^{j/m}\Bigl(\int_X|\phi|{}^2\Bigr)^{(m-j)/m}\notag \\ &=\Vert\lvert x\rvert^m\phi\Vert^{2j/m}\Vert\phi\Vert^{2(m-j)/m}, \end{aligned} $$

(A.1)

where we used Hölder’s inequality with $f=\lvert x\rvert ^{2j}|\phi |{ }^{2j/m}$ and $g=|\phi |{ }^{(2m-2j)/m}$. It follows that $\Vert \lvert x\rvert ^j\phi \Vert ^m\leq \Vert \lvert x\rvert ^m\phi \Vert ^j\Vert \phi \Vert ^{m-j}$. In particular,

$$\displaystyle \begin{aligned} {} \liminf_{t\to+\infty}\frac{\Vert\lvert x\rvert^m\mathrm{e}^{-\mathrm{i} tH}\psi\Vert^2}{t^{2m}} \geq\Big(\liminf_{t\to+\infty} \frac{\Vert\lvert x\rvert\mathrm{e}^{-\mathrm{i} tH}\psi\Vert^{2}}{t^2}\Big)^m\Vert\psi\Vert^{2-2m}. \end{aligned} $$

(A.2)

On $\mathbb {R}^d$ we usually consider $\Vert x^j\phi \Vert$ instead of $\Vert \lvert x\rvert ^j\phi \Vert$, where $x^j\phi :=(x_1^j\phi ,\dots ,x_d^j\phi )$. We have $\Vert x_k^j\phi \Vert ^2\leq \Vert x_k^m\phi \Vert ^{2j/m}\Vert \phi \Vert ^{2(m-j)/m}$ by the same argument. Using the Plancherel identity gives the Gagliardo–Nirenberg inequality

$$\displaystyle \begin{aligned} \Vert D_k^j\phi\Vert\leq\Vert D_k^m\phi\Vert^{j/m}\Vert\phi\Vert^{(m-j)/m}. \end{aligned}$$

If H is a Schrödinger operator and

$$\displaystyle \begin{aligned} x^j_k(t):=\mathrm{e}^{\mathrm{i} tH}x^j_k\mathrm{e}^{-\mathrm{i} tH},\quad D^j_k(t):=\mathrm{e}^{\mathrm{i} tH}(-\mathrm{i}\partial_{x_k})^j\mathrm{e}^{-\mathrm{i} tH}, \end{aligned}$$

then this implies

$$\displaystyle \begin{aligned} {} \begin{aligned} \Vert x_k^j(t)\psi\Vert&\leq\Vert x_k^m(t)\psi\Vert^{j/m}\Vert\psi\Vert^{(m-j)/m},\\ \Vert D_k^j(t)\psi\Vert&\leq\Vert D_k^m(t)\psi\Vert^{j/m}\Vert\psi\Vert^{(m-j)/m}. \end{aligned} \end{aligned} $$

(A.3)

Lastly in this connection, recall the uncertainty principle $\Vert \phi \Vert ^2\leq 2\Vert x_k\phi \Vert \Vert \partial _{x_k}\phi \Vert$. The above yields the generalization

$$\displaystyle \begin{aligned} \Vert\phi\Vert^2\leq 2\Vert x_k^m\phi\Vert^{1/m}\Vert\phi\Vert^{(m-1)/m}\Vert\partial_{x_k}^m\phi\Vert^{1/m}\Vert\phi\Vert^{(m-1)/m}, \end{aligned}$$

i.e.

$$\displaystyle \begin{aligned} {} \Vert\phi\Vert^2 \leq 2^m \Vert x_k^m\phi\Vert\cdot\Vert D_k^m\phi\Vert. \end{aligned} $$

(A.4)

Applying this to $\phi =\mathrm{e} ^{-\mathrm{i} tH}\psi$, we thus get

$$\displaystyle \begin{aligned} {} \Vert x_k^j(t)\psi\Vert\cdot\Vert D_k^j(t)\psi\Vert\leq 2^{m-j}\Vert x_k^m(t)\psi\Vert\cdot\Vert D_k^m(t)\psi\Vert. \end{aligned} $$

(A.5)

More generally, for $j,n\leq m$,

$$\displaystyle \begin{aligned} {} \Vert x_k^j(t)\psi\Vert\cdot\Vert D_k^n(t)\psi\Vert\leq 2^{\frac{2m-j-n}{2}}\Vert x_k^m(t)\psi\Vert^{\frac{2m+j-n}{2m}}\Vert D_k^m(t)\psi\Vert^{\frac{2m-j+n}{2m}}. \end{aligned} $$

(A.6)

The preceding estimates provide useful lower bounds for $x^m(t)\psi$ and $D^m(t)\psi$ in terms of lower moments.

We now consider upper bounds.

1.2 A.2 Discrete Case

In the following, given a countable graph G, we fix some vertex $o\in G$ regarded as an origin and denote $\lvert x\rvert := d(x,o)$ and $x^m\psi (x):=\lvert x\rvert ^m\psi (x)$.

Theorem A.1

Let $H=\mathcal {A}+V$ be a Schrödinger operator on a countable graph G with maximal degree $\leq \mathrm {D}$. We assume the potential V  is bounded. Then for any $t\geq 0$ and $m\in \mathbb {N}$, if $\Vert x^m\psi \Vert <\infty$, then

$$\displaystyle \begin{aligned} {} \Vert x^m\mathrm{e}^{-\mathrm{i} tH}\psi\Vert\leq\sum_{r=0}^m p_{m-r}(t)\Vert x^r\psi\Vert, \end{aligned} $$

(A.7)

where $p_k(t)$ is a polynomial in t of degree k with $p_0(t)=1$, and the leading term of the top polynomial $p_m(t)$ is $\mathrm {D}^mt^m$. In particular,

$$\displaystyle \begin{aligned} {} \limsup_{t\to+\infty}\frac{\Vert x^m\mathrm{e}^{-\mathrm{i} tH}\psi\Vert}{t^m}\leq\mathrm{D}^m \Vert\psi\Vert. \end{aligned} $$

(A.8)

Note that each $p_k(t)$ also depends on m, that is, for each fixed m there is a set of polynomials $p_{0,m}(t),\dots ,p_{m,m}(t)$ with $p_{k,m}$ of degree k such that (A.7) is satisfied with $p_k\equiv p_{k,m}$. See Remark A.3 for a further comment.

Proof

By induction on m. The statement is trivial for $m=0$ since $\mathrm{e} ^{-\mathrm{i} tH}$ is unitary.

Let $m=1$. For an operator O, recall we denote $O(t):=\mathrm{e} ^{\mathrm{i} tH}O\mathrm{e} ^{-\mathrm{i} tH}$. In particular, $x(t):=\mathrm{e} ^{\mathrm{i} tH}x\mathrm{e} ^{-\mathrm{i} tH}$ when O is the operator of multiplication by x. We formally have

$$\displaystyle \begin{aligned} {} \frac{\mathrm{d}}{\mathrm{d} t} x(t)\psi &=\mathrm{i} H\mathrm{e}^{\mathrm{i} tH}x\mathrm{e}^{-\mathrm{i} tH}\psi-\mathrm{i}\mathrm{e}^{\mathrm{i} tH}x H\mathrm{e}^{-\mathrm{i} tH}\psi\notag\\ &=\mathrm{i}\mathrm{e}^{\mathrm{i} tH}[H,x]\mathrm{e}^{-\mathrm{i} tH}\psi\notag\\ &=\mathrm{i}\mathrm{e}^{\mathrm{i} tH}[\mathcal{A},x]\mathrm{e}^{-\mathrm{i} tH}\psi\,. \end{aligned} $$

(A.9)

This calculation is formal because the first term $\mathrm{i} H\mathrm{e} ^{\mathrm{i} tH}x\mathrm{e} ^{-\mathrm{i} tH}\psi$ in the derivative requires $x\mathrm{e} ^{-\mathrm{i} tH}\psi \in \ell ^2(G)$, while the second term $-\mathrm{i} \mathrm{e} ^{\mathrm{i} tH}x H\mathrm{e} ^{-\mathrm{i} tH}\psi$ requires $\lim _{\delta \to 0}x\frac {\mathrm{e} ^{-\mathrm{i} (t+\delta )H}-\mathrm{e} ^{-\mathrm{i} tH}}{\delta }\psi =-\mathrm{i} xH\mathrm{e} ^{-\mathrm{i} tH}\psi$. See, e.g., [15, Lemma 10.17]. None of these facts is a priori clear (in fact the first point is partly what the theorem tries to prove, we only know that $x\psi \in \ell ^2(G)$, a priori). Note that this formal calculation is justified however if instead of x we multiply by a bounded function.

So, similar to [27], given $\epsilon >0$, we consider $f_{\epsilon }(\lambda ):=\frac {\lambda }{1+\epsilon \lambda }$ for $\lambda \geq 0$. Then multiplication by $f_{\epsilon }(\lvert x\rvert )$ is a bounded operator and we have $\frac {\mathrm{d} }{\mathrm{d} t} [f_{\epsilon }(\lvert x\rvert )](t)=\mathrm{i} \mathrm{e} ^{\mathrm{i} t H}[\mathcal {A},f_{\epsilon }(\lvert x\rvert )]\mathrm{e} ^{-\mathrm{i} tH}\psi$. But

$$\displaystyle \begin{aligned} [\mathcal{A},f_{\epsilon}(\lvert x\rvert)]\phi(x)=\sum_{y\sim x}[f_\epsilon(|y|) - f_\epsilon(\lvert x\rvert)]\phi(y) =:\sum_{y\sim x}\alpha_{x,y}\phi(y). \end{aligned}$$

Here $|\alpha _{x,y}|=|f_{\epsilon }^{\prime }(\lambda )|$ for some $\lambda \in [\lvert x\rvert -1,\lvert x\rvert +1]$. Hence, $|\alpha _{x,y}|\leq \frac {1}{(1+\epsilon \lambda )^2}\leq 1$. We thus get

$$\displaystyle \begin{aligned} \Vert[\mathcal{A},f_{\epsilon}(\lvert x\rvert)]\phi\Vert^2\leq\mathrm{D}\sum_x\sum_{y\sim x}|\phi(y)|{}^2\leq\mathrm{D}^2\Vert\phi\Vert^2. \end{aligned}$$

Applying this to $\phi =\mathrm{e} ^{-\mathrm{i} tH}\psi$, we get $\Vert [\mathcal {A},f_{\epsilon }(\lvert x\rvert )]\mathrm{e} ^{-\mathrm{i} tH}\psi \Vert \leq \mathrm {D} \Vert \psi \Vert$. So using [8, Theorem 5.6.1],

$$\displaystyle \begin{aligned} \Vert(f_\epsilon(\lvert x\rvert))(t)\psi\Vert &= \Bigl\Vert(f_\epsilon(\lvert x\rvert))(0)\psi + \int_0^t\frac{\mathrm{d}}{\mathrm{d} s}(f_\epsilon(\lvert x\rvert))(s)\psi\,\mathrm{d} s\Bigr\Vert\\ &\leq \Vert f_\epsilon(\lvert x\rvert)\psi\Vert + \int_0^t \Vert[\mathcal{A},f_\epsilon(\lvert x\rvert)]\mathrm{e}^{-\mathrm{i} sH}\psi\Vert\,\mathrm{d} s\\ &\leq \Vert x\psi\Vert + t\mathrm{D}\Vert\psi\Vert\,. \end{aligned} $$

Since $\epsilon >0$ is arbitrary, taking $\epsilon \downarrow 0$ and using Fatou’s lemma, we get

$$\displaystyle \begin{aligned} {} \Vert x\mathrm{e}^{-\mathrm{i} tH}\psi\Vert^2=\sum_x\lvert x\rvert^2|(\mathrm{e}^{-\mathrm{i} tH}\psi)(x)|{}^2 &\leq\liminf_{\epsilon\downarrow 0}\sum_x\frac{\lvert x\rvert^2}{(1+\epsilon \lvert x\rvert)^2}|(\mathrm{e}^{-\mathrm{i} tH}\psi)(x)|{}^2\notag\\ &= \liminf_{\epsilon\downarrow 0} \Vert f_\epsilon(\lvert x\rvert)\mathrm{e}^{-\mathrm{i} tH}\psi\Vert^2\notag\\ &\leq (\Vert x\psi\Vert + t\mathrm{D}\Vert\psi\Vert)^2, \end{aligned} $$

(A.10)

where we used $\Vert f_\epsilon (\lvert x\rvert )\mathrm{e} ^{-\mathrm{i} tH}\psi \Vert =\Vert (f_\epsilon (\lvert x\rvert ))(t)\psi \Vert$ since $\mathrm{e} ^{\mathrm{i} tH}$ is unitary. This settles $m=1$.

Now assume the statement holds for all $k<m$. Let $f_\epsilon (\lambda )=\frac {\lambda ^m}{1+\epsilon \lambda ^m}$. Here $|f_\epsilon '(\lambda )|\leq m|\lambda |{ }^{m-1}$. Arguing as before, we get

$$\displaystyle \begin{aligned} \Vert[\mathcal{A},f_{\epsilon}(\lvert x\rvert)]\phi\Vert^2 &\leq \mathrm{D}m^2\sum_x(\lvert x\rvert+1)^{2(m-1)}\sum_{y\sim x}|\phi(y)|{}^2\\ &\leq \mathrm{D}^2m^2 \Vert(\lvert x\rvert+2)^{m-1}\phi\Vert^2\,. \end{aligned} $$

Hence,

$$\displaystyle \begin{aligned} \Vert(f_\epsilon(\lvert x\rvert))(t)\psi\Vert\leq \Vert f_\epsilon(\lvert x\rvert)\psi\Vert + \mathrm{D}m\sum_{q=0}^{m-1}\binom{m-1}{q}2^{m-1-q}\int_0^t \Vert x^q\mathrm{e}^{-\mathrm{i} sH}\psi\Vert\,\mathrm{d} s. \end{aligned}$$

Since $f_\epsilon (\lvert x\rvert )\leq \lvert x\rvert ^m$, using the induction hypothesis we get

$$\displaystyle \begin{aligned} \Vert(f_\epsilon(\lvert x\rvert))(t)\psi\Vert\leq \Vert x^m\psi\Vert+\mathrm{D}m\sum_{q=0}^{m-1}\binom{m-1}{q}2^{m-1-q}\sum_{r=0}^q\tilde{p}_{q-r+1}(t)\Vert x^r\psi\Vert\,. \end{aligned}$$

As the RHS is independent of $\epsilon$, taking $\epsilon \downarrow 0$ and using Fatou’s lemma again yields $\Vert x^m(t)\psi \Vert \leq \sum _{s=0}^m p_{m-s}(t)\Vert x^s\psi \Vert$. The above also shows the coefficient of $\Vert x^m\psi \Vert$ is $p_0(t)=1$. The top polynomial $p_m(t)$ is found by taking $q=m-1$ and $r=0$ and equals $\mathrm {D}m\tilde {p}_m(t)$, where $\tilde {p}_m(t):=\int _0^t p_{m-1}(s)\,\mathrm{d} s$. As the leading term of $p_{m-1}(s)$ is $\mathrm {D}^{m-1}s^{m-1}$ by hypothesis, the leading term of $\mathrm {D}m\int _0^t p_{m-1}(s)\,\mathrm{d} s$ is $\mathrm {D}^m t^m$. □

A posteriori, the formal differentiation (A.9) is actually valid. Recall the notation $x(t):=\mathrm{e} ^{\mathrm{i} tH}x\mathrm{e} ^{-\mathrm{i} tH}$.

Corollary A.2

Under the same assumptions, $\lim \limits _{s\to t}x^m(s)\psi =x^m(t)\psi$ and

$$\displaystyle \begin{aligned} {} \frac{\mathrm{d}}{\mathrm{d} t}x^m(t)\psi=\mathrm{i}\mathrm{e}^{\mathrm{i} tH}[\mathcal{A},x^m]\mathrm{e}^{-\mathrm{i} tH}\psi\,. \end{aligned} $$

(A.11)

Proof

We have

$$\displaystyle \begin{aligned} {} &\Vert x^m(s)\psi - x^m(t)\psi\Vert = \Vert\mathrm{e}^{\mathrm{i} sH}x^m\mathrm{e}^{-\mathrm{i} sH}\psi - \mathrm{e}^{\mathrm{i} tH}x^m\mathrm{e}^{-\mathrm{i} tH}\psi\Vert\notag \\ &\quad \leq \Vert\mathrm{e}^{\mathrm{i} sH} x^m \mathrm{e}^{-\mathrm{i} sH}\psi - \mathrm{e}^{\mathrm{i} sH} x^m \mathrm{e}^{-\mathrm{i} tH}\psi\Vert + \Vert\mathrm{e}^{\mathrm{i} sH}x^m\mathrm{e}^{-\mathrm{i} tH}\psi - \mathrm{e}^{\mathrm{i} tH}x^m\mathrm{e}^{-\mathrm{i} tH}\psi\Vert\notag\\ &\quad = \Vert x^m \mathrm{e}^{-\mathrm{i} sH}\psi - x^m \mathrm{e}^{-\mathrm{i} tH}\psi\Vert + \Vert\mathrm{e}^{\mathrm{i} sH}x^m\mathrm{e}^{-\mathrm{i} tH}\psi - \mathrm{e}^{\mathrm{i} tH}x^m\mathrm{e}^{-\mathrm{i} tH}\psi\Vert\,. \end{aligned} $$

(A.12)

We know from Theorem A.1 that $\phi =x^m\mathrm{e} ^{-\mathrm{i} tH}\psi \in D(H)=\ell ^2(G)$ for any $t\geq 0$, so $\lim _{s\to t}\mathrm{e} ^{\mathrm{i} sH}x^m\mathrm{e} ^{-\mathrm{i} tH}\psi =\mathrm{e} ^{\mathrm{i} tH}x^m\mathrm{e} ^{-\mathrm{i} tH}\psi$. This settles the second term in the RHS.

For the first term, we use Fatou’s lemma as in (A.10). Let $f_\epsilon (\lambda )=\frac {\lambda ^m}{1+\epsilon \lambda ^m}$. We have $f_{\epsilon }(\lvert x\rvert )\mathrm{e} ^{-\mathrm{i} tH}\psi =f_\epsilon (\lvert x\rvert )\mathrm{e} ^{-\mathrm{i} sH}\psi +\int _s^t\frac {\mathrm{d} }{\mathrm{d} \alpha }f_\epsilon (\lvert x\rvert )\mathrm{e} ^{-\mathrm{i} \alpha H}\psi \,\mathrm{d} \alpha$. Now

$$\displaystyle \begin{aligned} \Bigl\Vert\frac{\mathrm{d}}{\mathrm{d} \alpha}f_\epsilon(\lvert x\rvert)\mathrm{e}^{-\mathrm{i}\alpha H}\psi\Bigr\Vert&= \Vert f_\epsilon(\lvert x\rvert)H\mathrm{e}^{-\mathrm{i}\alpha H}\psi\Vert\\ &\leq \Vert x^m \mathrm{e}^{-\mathrm{i}\alpha H}H\psi\Vert \leq \sum_{r=0}^{m} p_{m-r}(\alpha)\Vert x^r H\psi\Vert \end{aligned} $$

for some polynomials $p_k$, by Theorem A.1. These are uniformly bounded by some $M(t)$ for all $\alpha \in [t-1,t+1]$ and we get $\Vert f_\epsilon (\lvert x\rvert ) \mathrm{e} ^{-\mathrm{i} sH}\psi - f_\epsilon (\lvert x\rvert ) \mathrm{e} ^{-\mathrm{i} tH}\psi \Vert \leq \left |t-s\right |M(t)\sum _{r=0}^{m}\Vert x^rH\psi \Vert$, with $M(t)$ independent of $\epsilon$.

By Fatou’s lemma, $\Vert x^m \mathrm{e} ^{-\mathrm{i} sH}\psi - x^m \mathrm{e} ^{-\mathrm{i} tH}\psi \Vert ^2 \leq \liminf \limits _{\epsilon \to 0}\Vert f_\epsilon (\lvert x\rvert ) \mathrm{e} ^{-\mathrm{i} sH}\psi - f_\epsilon (\lvert x\rvert ) \mathrm{e} ^{-\mathrm{i} tH}\psi \Vert ^2$. Thus, $\Vert x^m \mathrm{e} ^{-\mathrm{i} sH}\psi - x^m \mathrm{e} ^{-\mathrm{i} tH}\psi \Vert \leq \left |t-s\right |M(t)\sum _{r=0}^{m-1}\Vert x^rH\psi \Vert \to 0$ as $s\to t$. Recalling (A.12), this completes the proof of the first claim.

For the derivative we first make some simplifications. Given $\delta >0$,

$$\displaystyle \begin{aligned} {} &\Bigl\Vert\frac{x^m(t+\delta)\psi - x^m(t)\psi}{\delta} - \mathrm{i}\mathrm{e}^{\mathrm{i} tH}[H,x^m]\mathrm{e}^{-\mathrm{i} tH}\psi\Bigr\Vert \notag\\ &\quad =\Bigl\Vert\frac{\mathrm{e}^{\mathrm{i}\delta H} x^m\mathrm{e}^{-\mathrm{i}(t+\delta)H}\psi - x^m\mathrm{e}^{-\mathrm{i} tH}\psi}{\delta} - \mathrm{i} [H,x^m]\mathrm{e}^{-\mathrm{i} tH}\psi\Bigr\Vert \notag\\ &\quad \leq \Bigl\Vert\frac{\mathrm{e}^{\mathrm{i}\delta H} - I}{\delta}x^m\mathrm{e}^{-\mathrm{i}(t+\delta)H}\psi - \mathrm{i} H x^m\mathrm{e}^{-\mathrm{i}(t+\delta)H}\psi\Bigr\Vert \notag\\ &\qquad + \Vert Hx^m(\mathrm{e}^{-\mathrm{i} tH}\psi-\mathrm{e}^{-\mathrm{i}(t+\delta)H})\psi\Vert \notag\\ &\qquad + \Bigl\Vert x^m\Bigl(\frac{\mathrm{e}^{-\mathrm{i}(t+\delta)H} - \mathrm{e}^{-\mathrm{i} tH}}{\delta}\psi +\mathrm{i} H\mathrm{e}^{-\mathrm{i} tH}\psi\Bigr)\Bigr\Vert\notag\\ &\quad \leq \Bigl\Vert\Bigl(\frac{\mathrm{e}^{\mathrm{i}\delta H} - I}{\delta}-\mathrm{i} H\Bigr)x^m\mathrm{e}^{-\mathrm{i} tH}\psi\Bigr\Vert\notag\\ &\qquad +\Bigl\Vert\Bigl(\frac{\mathrm{e}^{\mathrm{i}\delta H} - I}{\delta}-\mathrm{i} H\Bigr)x^m(\mathrm{e}^{-\mathrm{i}(t+\delta)H}\psi - \mathrm{e}^{-\mathrm{i} tH}\psi)\Bigr\Vert\notag\\ &\qquad + \Vert Hx^m(\mathrm{e}^{-\mathrm{i} tH}\psi-\mathrm{e}^{-\mathrm{i}(t+\delta)H})\psi\Vert \notag\\ &\qquad + \Bigl\Vert x^m\Big(\frac{\mathrm{e}^{-\mathrm{i}(t+\delta)H} - \mathrm{e}^{-\mathrm{i} tH}}{\delta}\psi +\mathrm{i} H\mathrm{e}^{-\mathrm{i} tH}\psi\Big)\Bigr\Vert\,. \end{aligned} $$

(A.13)

For the first term, we know from Theorem A.1 that $x^m\mathrm{e} ^{-\mathrm{i} tH}\psi \in D(H)=\ell ^2(G)$, so this term vanishes as $\delta \to 0$. For the second term, we use the spectral theorem: $\Vert \frac {\mathrm{e} ^{\mathrm{i} \delta H}-I}{\delta }\phi \Vert ^2=\int |\frac {\mathrm{e} ^{\mathrm{i} \delta \lambda }-1}{\delta }|{ }^2\,\mathrm{d} \mu _\phi (\lambda )\leq \int \lambda ^2\,\mathrm{d} \mu _\phi (\lambda )=\Vert H\phi \Vert ^2$. With this bound, we see the second and third terms vanish as $\delta \to 0$ by the argument of (A.12) (note that H is bounded; see also Corollary A.5 for unbounded operators). So it remains to control the last term. For this we first use Fatou’s lemma to replace $x^m$ by $f_\epsilon (\lvert x\rvert )$ as follows.

We know that

$$\displaystyle \begin{aligned} \frac{\mathrm{d}}{\mathrm{d} s} f_\epsilon(\lvert x\rvert)\mathrm{e}^{-\mathrm{i} sH}\psi&=f_\epsilon(\lvert x\rvert)(-\mathrm{i} H\mathrm{e}^{-\mathrm{i} sH})\psi,\\ \frac{\mathrm{d}}{\mathrm{d} s} f_\epsilon(\lvert x\rvert)(-\mathrm{i} H\mathrm{e}^{-\mathrm{i} sH}\psi)&=-f_\epsilon(\lvert x\rvert) H^2\mathrm{e}^{-\mathrm{i} sH}\psi. \end{aligned} $$

It follows from [8, Theorem 5.6.2] that for small $\delta$,

$$\displaystyle \begin{aligned} \Bigl\Vert f_\epsilon(\lvert x\rvert)\Big(\frac{\mathrm{e}^{-\mathrm{i}(t+\delta)H} - \mathrm{e}^{-\mathrm{i} tH}}{\delta}\psi +\mathrm{i} H\mathrm{e}^{-\mathrm{i} tH}\psi\Big)\Bigr\Vert \leq \frac{\lvert\delta\rvert}{2}\sup_{s\in [t-1,t+1]} \Vert x^mH^2\mathrm{e}^{-\mathrm{i} sH}\psi\Vert, \end{aligned}$$

where we used that $f_\epsilon (\lvert x\rvert )\leq \lvert x\rvert ^m$. Using Theorem A.1 again, we may bound the RHS by $\frac {\lvert \delta \rvert }{2}M(t)\sum _{r=0}^m\Vert x^r H^2\psi \Vert$, with $M(t)$ independent of $\epsilon$. Fatou’s lemma implies as before that the last term in (A.13) is now bounded by $\frac {\lvert \delta \rvert }{2}M(t)\sum _{r=0}^m\Vert x^rH^2\psi \Vert$. Taking $\delta \to 0$ finally completes the proof. □

Remark A.3

Theorem A.1 implies that

$$\displaystyle \begin{aligned} \limsup_{t\to+\infty}\frac{1}{t^{2m}}\sum_{x\in G}\lvert x\rvert^{2m}|\mathrm{e}^{-\mathrm{i} tH}\psi(x)|{}^2 \leq \mathrm{D}^{2m}\Vert\psi\Vert^2. \end{aligned}$$

This also implies a control for odd powers. Namely, if $\Vert x^m\psi \Vert <\infty$, letting $\psi _t:=\mathrm{e} ^{-\mathrm{i} tH}\psi$, we have by Cauchy–Schwarz that

$$\displaystyle \begin{aligned} \sum \lvert x\rvert^m |\psi_t(x)|{}^2 \leq\Bigl(\sum \lvert x\rvert^{2m}|\psi_t(x)|{}^2\Bigr)^{1/2}\Bigl(\sum|\psi_t(x)|{}^2\Bigr)^{1/2}. \end{aligned}$$

So $\frac {1}{t^m}\sum \lvert x\rvert ^m |\psi _t(x)|{ }^2 \leq (\frac {1}{t^{2m}}\sum \lvert x\rvert ^{2m}|\psi _t(x)|{ }^2)^{1/2}\Vert \psi \Vert$ and thus

$$\displaystyle \begin{aligned} \limsup_{t\to+\infty}\frac{1}{t^{m}}\sum_{x\in G}\lvert x\rvert^{m}|\psi_t(x)|{}^2 \leq\mathrm{D}^{m}\Vert\psi\Vert^2. \end{aligned}$$

1.3 A.3 Continuous Case

Assume now that on $\mathbb {R}^d$, we have a potential $V\in C^{m-1}$ such that V  and its partial derivatives of order $<m$ are bounded. Let $H=H_0+V=-\Delta +V$. Then we claim that

$$\displaystyle \begin{aligned} {} \Vert D^m\phi\Vert\leq C_{m,V}\sum_{k=0}^m\Vert H^k\phi\Vert. \end{aligned} $$

(A.14)

Indeed, using $X^m-Y^m=\sum _{p=0}^{m-1}X^p(X-Y)Y^{m-1-p}$, we have

$$\displaystyle \begin{aligned} \Vert D^m\phi\Vert^2=\langle\phi,D^{2m}\phi\rangle\leq\langle\phi,H_0^m\phi\rangle= \langle\phi,H^m\phi\rangle-\sum_{p=0}^{m-1}\langle\phi,H_0^pVH^{m-1-p}\phi\rangle. \end{aligned}$$

with the convention $\sum _{p=0}^{-1}:= 0$.

Now (A.14) is clear for $m=0$. If (A.14) holds for all $p<m$, then using Cauchy–Schwarz, Leibniz formula, and our assumption on V , we get

$$\displaystyle \begin{aligned} |\langle\phi, H_0^p VH^{m-1-p}\phi\rangle| &\leq c_{d,p}\Vert D^p\phi\Vert\cdot\Vert D^p VH^{m-1-p}\phi\Vert\\ &\leq c_{V,m} \sum_{q=0}^p \Vert D^p\phi\Vert\cdot\Vert D^qH^{m-1-p}\phi\Vert. \end{aligned} $$

So by induction hypothesis,

$$\displaystyle \begin{aligned} \Vert D^m\phi\Vert^2 \leq \Vert\phi\Vert\cdot\Vert H^m\phi\Vert + c_{V,m}^{\prime}\sum_{p=0}^{m-1}\sum_{r=0}^p\sum_{q=0}^p\sum_{s=0}^q \Vert H^r\phi\Vert\cdot\Vert H^{m-1-p+s}\phi\Vert. \end{aligned}$$

Using $ab\leq \frac {1}{2}(a^2+b^2)$, we thus get $\Vert D^m\phi \Vert ^2 \leq c_{V,m}^{\prime \prime }\sum _{k=0}^m\Vert H^k\phi \Vert ^2$, implying (A.14). This implies that for $D(t):=\mathrm{e} ^{\mathrm{i} tH}D\mathrm{e} ^{-\mathrm{i} tH}$ and $\psi _t:=\mathrm{e} ^{-\mathrm{i} tH}\psi$, we have

$$\displaystyle \begin{aligned} {} \Vert D(t)^r\psi\Vert=\Vert D^r\psi_t\Vert\leq C_{r,V}\sum_{k=0}^r\Vert H^k\psi\Vert \leq C_{r,V}^{\prime}\Vert\psi\Vert_{H^{2r}}, \end{aligned} $$

(A.15)

independently of t, where we used that $H^k\mathrm{e} ^{-\mathrm{i} tH}=\mathrm{e} ^{-\mathrm{i} tH}H^k$.

Theorem A.4

If $V\in C^{m-1}(\mathbb {R}^d)$, if V  and its partial derivatives of order $<m$ are bounded, and if $\psi \in H^{2m}(\mathbb {R}^d)$, then

$$\displaystyle \begin{aligned} \Vert x^m\mathrm{e}^{-\mathrm{i} tH}\psi\Vert\leq 2^{m-1}\Bigl(\Vert x^m\psi\Vert+C_mt^m \sum_{k=0}^m\Vert H^k\psi\Vert\Bigr). \end{aligned}$$

A sketch of an earlier result can also be found in [27, Theorem 4.1]. We first give a formal proof, then indicate how to make it rigorous.

Proof (Formal)

Recall that $x^m=(x_1^m,\dots ,x_d^m)$. In this proof we denote $x^{2m}= x_1^{2m}+\dots +x_d^{2m}$ instead of $\lvert x^m\rvert _2^2$ to avoid too cumbersome formulas.

Formally, $\frac {\mathrm{d} }{\mathrm{d} t} x^{2m}(t)\psi =\mathrm{i} \mathrm{e} ^{\mathrm{i} tH}[-\Delta , x^{2m}]\mathrm{e} ^{-\mathrm{i} tH}\psi$ for $\psi \in D(H)$. But, for F smooth on $\mathbb {R}^d$ we have $[-\Delta ,F]\phi =-(\Delta F)\phi - 2\nabla F\cdot \nabla \phi =-\nabla \cdot [(\nabla F)\phi ]-\nabla F\cdot \nabla \phi$. In particular, for $F(x)=x^{2m}$, since $\nabla x^{2m}=2m(x_1^{2m-1},\dots ,x_d^{2m-1})$, we get

$$\displaystyle \begin{aligned} \frac{\mathrm{d}}{\mathrm{d} t}\Vert x^m(t)\psi\Vert^2&=\frac{\mathrm{d}}{\mathrm{d} t}\langle\psi,x^{2m}(t)\psi\rangle\\ &= \mathrm{i}\langle\psi_t,[-\Delta,x^{2m}] \psi_t\rangle \\ &= \langle\psi, D(t)\cdot[(\nabla x^{2m})(t)\psi] + (\nabla x^{2m})(t)\cdot D(t)\psi\rangle\\ &\leq 4m \sum_{j=1}^d\Vert x_j^m(t)\psi\Vert\cdot\Vert x_j^{m-1}(t)D_j(t)\psi\Vert, \end{aligned} $$

where $D_j:=-\mathrm{i} \partial _{x_j}$ and $D_j(t):=\mathrm{e} ^{\mathrm{i} tH}D_j\mathrm{e} ^{-\mathrm{i} tH}$. We have in general

$$\displaystyle \begin{aligned} \Vert x_j^n(t)D_j^k(t)\psi\Vert&=\langle\psi,D_j^k(t)x_j^{2n}(t)D_j^k(t)\psi\rangle^{1/2}\notag\\ {} &\leq\sum_{p=0}^k\binom{k}{p}(2n)\cdots(2n-p)\lvert\langle\psi,x_j^{2n-p}(t)D_j^{2k-p}(t)\psi\rangle\rvert^{1/2} \end{aligned} $$

(A.16)

$$\displaystyle \begin{aligned} {} &\leq\sum_{p=0}^k c_{p,k,n}\Vert x_j^m(t)\psi\Vert^{1/2}\Vert x_j^{2n-p-m}(t)D_j^{2k-p}(t)\psi\Vert^{1/2}. \end{aligned} $$

(A.17)

We may apply the same inequality to $\Vert x_j^{2n-p-m}(t)D_j^{2k-p}(t)\psi \Vert$. Doing this $\ell -1$ times we see that the term with highest power is

$$\displaystyle \begin{aligned} C_{k,n}\Vert x_j^m(t)\psi\Vert^{\frac{1}{2}+\frac{1}{4}+\dots+\frac{1}{2^{\ell-1}}}\Vert x_j^{2^{\ell-1}(n-m)+m}(t)D_j^{2^{\ell-1}k}(t)\psi\Vert^{\frac{1}{2^{\ell-1}}}. \end{aligned}$$

The Case$m=2^\ell$ Let $n=m-1=2^\ell -1$. Then by applying (A.17) $\ell -1$ times, we get

$$\displaystyle \begin{aligned} {} \frac{\mathrm{d}}{\mathrm{d} t}\Vert x(t)^m\psi\Vert^2\leq C_m\sum_{j=1}^d\Vert x_j^m(t)\psi\Vert\cdot\Vert x_j^m(t)\psi\Vert^{1-\frac{1}{2^{\ell-1}}}\sum_{r=0}^{2^{\ell-1}}c_{r,m}\Vert x_j^r(t)D_j^r(t)\psi\Vert^{\frac{1}{2^{\ell-1}}}. \end{aligned} $$

(A.18)

In fact, the terms have the general form

$$\displaystyle \begin{aligned} x_j^{2^{\ell-1}(n-m)+m-2^{\ell-2}p_1-2^{\ell-3}p_2-\dots-p_{\ell-1}}(t)D_j^{2^{\ell-1}k-2^{\ell-2}p_1-\dots-p_{\ell-1}}(t)\psi. \end{aligned}$$

For $m=2^\ell$, $n=m-1$, $k=1$, we see the powers of $x_j(t)$ and $D_j(t)$ match indeed.

We next apply (A.16) plus Cauchy–Schwarz to get

$$\displaystyle \begin{aligned} {} &\frac{\mathrm{d}}{\mathrm{d} t}\Vert x^m(t)\psi\Vert^2\notag\\ &\qquad \leq C_m\sum_{j=1}^d\Vert x_j^m(t)\psi\Vert^{2-\frac{1}{2^{\ell-1}}}\sum_{r=0}^{2^{\ell-1}} c_{r,m}\sum_{p=0}^rc_{p,r}\Vert x_j^{2r-p}(t)\psi\Vert^{\frac{1}{2^\ell}}\Vert D_j^{2r-p}(t)\psi\Vert^{\frac{1}{2^{\ell}}}\,. \end{aligned} $$

(A.19)

Recalling (A.5) and (A.15), we conclude that for $m=2^\ell$,

$$\displaystyle \begin{aligned} {} \frac{\mathrm{d}}{\mathrm{d} t}\Vert x^m(t)\psi\Vert^2 &\leq C_{m,d}\sum_{j=1}^d\Vert x_j^m(t)\psi\Vert^{2-\frac{1}{m}}\Vert D_j^m(t)\psi\Vert^{1/m}\notag\\ &\leq C_{m,d,V}\Vert x^m(t)\psi\Vert^{2-\frac{1}{m}}\sum_{k=0}^m\Vert H^k\psi\Vert^{1/m}. \end{aligned} $$

(A.20)

Thus,

$$\displaystyle \begin{aligned} \frac{\mathrm{d}}{\mathrm{d} t}\langle\psi,x^{2m}(t)\psi\rangle^{\frac{1}{2m}}=\frac{1}{2m}\langle\psi,x^{2m}(t)\psi\rangle^{\frac{1}{2m}-1}\frac{\mathrm{d}}{\mathrm{d} t}\langle\psi,x^{2m}(t)\psi\rangle\leq c\sum_{k=0}^m\Vert H^k\psi\Vert^{1/m}. \end{aligned}$$

We thus have $\Vert x^m(t)\psi \Vert ^{1/m}\leq \Vert x^m\psi \Vert ^{1/m}+ Ct\sum _{k=0}^m\Vert H^k\psi \Vert ^{1/m}$. The result follows in this case. □

The General Case For general m we let $\ell$ such that $2^{\ell } \leq m < 2^{\ell +1}$. Say $m=2^\ell +q$ with $0\leq q<2^\ell$. Then following the scheme, we apply (A.17) $\ell -1$ times. Then $\Vert x_j^r(t)D_j^r(t)\psi \Vert ^{\frac {1}{2^{\ell -1}}}$ in (A.18) is replaced by $\Vert x_j^{r+q}(t)D_j^r(t)\psi \Vert ^{\frac {1}{2^{\ell -1}}}$. The proof must be slightly modified as now $2r+2q\leq 2^\ell +2q=m+q$, i.e., the powers of $x_j(t)$ in (A.19) can exceed m. So to the q highest terms $r=2^{\ell -1}-q+1,\dots ,2^{\ell -1}$, we apply (A.17) once more to get $\sum _{p=0}^r c_{p,q,r}\Vert x_j^m(t)\psi \Vert ^{\frac {1}{2^\ell }}\Vert x_j^{2r+2q-p-m}(t)D_j^{2r-p}(t)\psi \Vert ^{\frac {1}{2^\ell }}$. We can now apply (A.16) plus Cauchy–Schwarz to this and the lower terms as before. Then (A.19) is replaced by

$$\displaystyle \begin{aligned} {} \frac{\mathrm{d}}{\mathrm{d} t}\Vert x(t)^m\psi\Vert^2 &\leq C_m\sum_{j=1}^d\Vert x_j^m(t)\psi\Vert^{2-\frac{1}{2^{\ell-1}}}\Big(\sum_{r=2^{\ell-1}-q+1}^{2^{\ell-1}}\sum_{p=0}^r c_{p,q,r}\Vert x_j^m(t)\psi\Vert^{\frac{1}{2^\ell}}\notag\\ &\times\sum_{p'=0}^{2r-p}c_{p',r,p,q,m}\Vert x_j^{4r+4q-2p-2m-p'}(t)\psi\Vert^{\frac{1}{2^{\ell+1}}}\Vert D_j^{4r-2p-p'}(t)\psi\Vert^{\frac{1}{2^{\ell+1}}}\notag\\ &+\sum_{r=0}^{2^{\ell-1}-q} c_{r,m}\sum_{p=0}^rc_{p,r}\Vert x_j^{2r+2q-p}(t)\Vert^{\frac{1}{2^\ell}}\Vert D_j^{2r-p}(t)\psi\Vert^{\frac{1}{2^{\ell}}}\Big)\,. \end{aligned} $$

(A.21)

We may now apply (A.6) and (A.15) to get

$$\displaystyle \begin{aligned} &\Vert x_j^{4r+4q-2p-2m-p'}(t)\psi\Vert\cdot\Vert D_j^{4r-2p-p'}(t)\psi\Vert\\ &\quad \leq 2^{2m-r-2q}\Vert x_j^m(t)\psi\Vert^{\frac{2q}{m}}\Vert D_j^m(t)\psi\Vert^{\frac{2m-2q}{m}}. \end{aligned} $$

Recall $q=m-2^{\ell }$, so $\frac {2q}{2^{\ell +1}m}=\frac {1}{2^\ell }-\frac {1}{m}$. In the first sum of (A.21), $\Vert x^m_j(t)\psi \Vert$ thus gets elevated to the power $2-\frac {1}{2^{\ell -1}}+\frac {1}{2^\ell }+\frac {1}{2^\ell }-\frac {1}{m}=2-\frac {1}{m}$ as required. For the lower terms, the power is similarly $2-\frac {1}{2^{\ell -1}}+\frac {2m+2q}{2^{\ell +1}m}=2-\frac {1}{m}$. This completes the formal proof. □

Proof (Completed)

To make the formal proof rigorous we consider the operator of multplication by

$$\displaystyle \begin{aligned} F_\epsilon(x):=\frac{x^{2m}}{1+\epsilon x^{2m}}=\frac{x_1^{2m}+\dots+x_d^{2m}}{1+\epsilon(x_1^{2m}+\dots+x_d^{2m})},\quad \epsilon>0. \end{aligned}$$

This is a bounded operator. For $F_\epsilon (x)(t):=\mathrm{e} ^{\mathrm{i} tH}F_\epsilon (x)\mathrm{e} ^{-\mathrm{i} tH}$ we get

$$\displaystyle \begin{aligned} \frac{\mathrm{d}}{\mathrm{d} t}F_\epsilon(x)(t)\psi=\mathrm{i}\mathrm{e}^{\mathrm{i} tH}[-\Delta, F_\epsilon(x)]\mathrm{e}^{-\mathrm{i} tH}\psi\text{ for }\psi\in D(H). \end{aligned}$$

Again $[-\Delta ,F_\epsilon ]\phi =-(\Delta F_\epsilon )\phi - 2\nabla F_\epsilon \cdot \nabla \phi =-\nabla \cdot [(\nabla F_\epsilon )\phi ]-\nabla F_\epsilon \cdot \nabla \phi$. On the other hand $\nabla F_\epsilon =2m(\frac {x_1^{2m-1}}{(1+\epsilon x^{2m})^2},\dots ,\frac {x_d^{2m-1}}{(1+\epsilon x^{2m})^2})$. So

$$\displaystyle \begin{aligned} &\frac{\mathrm{d}}{\mathrm{d} t}\langle\psi,F_\epsilon(x)(t)\psi\rangle=\langle\psi,D(t)\cdot [(\nabla F_\epsilon)(x)(t))\psi]+(\nabla F_\epsilon)(x)(t)\cdot D(t)\psi\rangle\\ &\qquad \quad =2m\sum_{j=1}^d\Bigl\langle\frac{x_j^{m-1}}{1+\epsilon x^{2m}}(t)D_j(t)\psi,\frac{x_j^{m}}{1+\epsilon x^{2m}}(t)\psi\Bigr\rangle\\ &\qquad \qquad \qquad \quad +\Bigl\langle\frac{x_j^{m}}{1+\epsilon x^{2m}}(t)\psi,\frac{x_j^{m-1}}{1+\epsilon x^{2m}}(t)D_j(t)\psi\Bigr\rangle\\ &\qquad \quad \leq 4m\sum_{j=0}^d\Bigl\Vert\frac{x_j^{m}}{1+\epsilon x^{2m}}(t)\psi\Bigr\Vert\,\Bigl\Vert\frac{x_j^{m-1}}{1+\epsilon x^{2m}}(t)D_j(t)\psi\Bigr\Vert. \end{aligned} $$

We have

$$\displaystyle \begin{aligned} \Bigl\Vert\frac{x_j^{m}}{1+\epsilon x^{2m}}(t)\psi\Bigr\Vert&=\Bigl\langle\psi_t,\frac{x_j^{2m}}{(1+\epsilon x^{2m})^2}\psi_t\Bigr\rangle^{1/2}\leq\langle\psi_t, F_\epsilon(x)\psi_t\rangle^{1/2}\\ &=\langle\psi,F_\epsilon(x)(t)\psi\rangle^{1/2} \end{aligned} $$

where $\psi _t:=\mathrm{e} ^{-\mathrm{i} tH}\psi$. On the other hand,

$$\displaystyle \begin{aligned} \Bigl\Vert\frac{x_j^r}{1+\epsilon x^{2m}}(t)D_j^k(t)\psi\Bigr\Vert &=\Bigl\langle\psi,D_j^k(t)\frac{x_j^{2r}}{(1+\epsilon x^{2m})^2}(t)D_j^k(t)\psi\Bigr\rangle^{1/2}\\ &\leq\sum_{p=0}^k \binom{k}{p}\Big\lvert\Bigl\langle\psi_t,D_j^p\frac{x_j^{2r}}{(1+\epsilon x^{2m})^2}D_j^{2k-p}\psi_t\Bigr\rangle\Big\rvert^{1/2} \end{aligned} $$

and

$$\displaystyle \begin{aligned} \partial_{x_j}^p\frac{x_j^{2r}}{(1+\epsilon x^{2m})^2}=\sum_{\ell=0}^p\binom{p}{\ell}(2r)\cdots(2r-\ell+1) x_j^{2r-\ell}\partial_{x_j}^{p-\ell}\frac{1}{(1+\epsilon x^{2m})^2}. \end{aligned}$$

If $f_\epsilon (u):=\frac {1}{(1+\epsilon u)^2}$ and $g(x):= x^{2m}$ then by the Faà di Bruno formula,

$$\displaystyle \begin{aligned} &\partial_{x_j}^n\frac{1}{(1+\epsilon x^{2m})^2}=\partial_{x_j}^nf_\epsilon(g(x))=\sum_{\substack{(m_1,\dots,m_n)\\ \sum_{i=1}^nim_i=n}}c_{n,m_i}f_\epsilon^{(m_1+\dots+m_n)}(g(x))\\ &\quad \times\prod_{i=1}^n(\partial_{x_j}^ig(x))^{m_i}\,. \end{aligned} $$

But $f_\epsilon ^{(q)}(u)=(-\epsilon )^q(q+1)!(1+\epsilon u)^{-2-q}$ and $\partial _{x_j}^ig(x)=(2m)\cdots (2m-i+1)x_j^{(2m-i)}$. Thus,

$$\displaystyle \begin{aligned} \partial_{x_j}^n\frac{1}{(1+\epsilon x^{2m})^2} &=\sum_{\substack{(m_1,\dots,m_n)\\ \sum_{i=1}^nim_i=n}}\tilde{c}_{n,m_i} \frac{\epsilon^{m_1+\dots+m_n}}{(1+\epsilon x^{2m})^{2+m_1+\dots+m_n}}(2m)x_j^{(2m-1)m_1}\\ &\quad \times (2m)(2m-1)x_j^{(2m-2)m_2}\cdots(2m)\cdots(2m-n+1)x_j^{(2m-n)m_n}\\ &=\sum_{\substack{(m_1,\dots,m_n)\\\sum_{i=1}^nim_i=n}}C_{n,m_i} \frac{\epsilon^{m_1+\dots+m_n}}{(1+\epsilon x^{2m})^{2+m_1+\dots+m_n}}x_j^{2m(m_1+\dots+m_n)-n}\,, \end{aligned} $$

where we used $\sum im_i=n$ in the last step. But

$$\displaystyle \begin{aligned} \epsilon ^{m_1+\dots+m_n}x_j^{2m(m_1+\dots+m_n)}\leq (1+\epsilon x^{2m})^{m_1+\dots+m_n}. \end{aligned}$$

Thus,

$$\displaystyle \begin{aligned} &\partial_{x_j}^p\frac{x_j^{2r}}{(1+\epsilon x^{2m})^2}\\ &\quad \leq\sum_{\ell=0}^p \binom{p}{\ell}(2r)\cdots(2r-\ell+1)x_j^{2r-\ell}\!\sum_{(m_1,\dots,m_{p-\ell})} C_{p-\ell,m_i}\frac{x_j^{\ell-p}}{(1+\epsilon x^{2m})^2}\\ &= \sum_{\ell=0}^p c_{p,\ell,r}\frac{x_j^{2r-p}}{(1+\epsilon x^{2m})^2}. \end{aligned} $$

It follows that

$$\displaystyle \begin{aligned} &\Bigl\Vert\frac{x_j^r}{1+\epsilon x^{2m}}(t)D_j^k(t)\psi\Bigr\Vert\\ &\quad \leq\sum_{p=0}^k c_{p,k,r}\Big\lvert\Bigl\langle\psi,\frac{x_j^{2r-p}}{(1+\epsilon x^{2m})^2}(t)D_j^{2k-p}(t)\psi\Bigr\rangle\Big\rvert^{1/2}\\ &\quad \leq\sum_{p=0}^k c_{p,k,r}\biggl\Vert\frac{x_j^m}{1+\epsilon x^{2m}}(t)\psi\biggr\Vert^{1/2}\,\biggl\Vert\frac{x_j^{2r-p-m}}{1+\epsilon x^{2m}}(t)D_j^{2k-p}(t)\psi\biggr\Vert^{1/2}. \end{aligned} $$

This proves the analog of (A.16)–(A.17). From here, the proof goes as before and we get

$$\displaystyle \begin{aligned} \Bigl\Vert\frac{x_j^m}{1+\epsilon x^{2m}}\psi\Bigr\Vert^{1/m}\leq\Vert x^m\psi\Vert^{1/m}+Ct\sum_{k=0}^m\Vert H^k\psi\Vert^{1/m}, \end{aligned}$$

independently of $\epsilon$. The result follows by taking $\epsilon \downarrow 0$, using Fatou’s lemma. □

Corollary A.5

Under the same assumptions on V , if $\psi \in H^{2m+4}(\mathbb {R}^d)$ and $x^m\psi \in L^2(\mathbb {R}^d)$, then

$$\displaystyle \begin{aligned} {} \frac{\mathrm{d}}{\mathrm{d} t}x^m(t)\psi=\mathrm{i}\mathrm{e}^{\mathrm{i} tH}[-\Delta,x^m]\mathrm{e}^{-\mathrm{i} tH}\psi. \end{aligned} $$

(A.22)

Proof

The proof is the same as that of Corollary A.2, using Theorem A.4. In more details, the fact that $x^m(s)\psi \to x^m(t)\psi$ as $s\to t$ for $\psi \in H^{2m+2}(\mathbb {R}^d)$ is proved the same way by considering $f_\epsilon (x):=\frac {x^m}{\sqrt {1+\epsilon x^{2m}}}$ instead. For the derivative, to deal with the second and third terms at the end of (A.13), we use that $Hx^m=x^m H + [-\Delta ,x^m]$ instead. The term $x^mH$ is dealt with as before. For the second term $[-\Delta ,x^m]$, let $\phi _t^\delta :=\mathrm{e} ^{-\mathrm{i} tH}\psi -\mathrm{e} ^{-\mathrm{i} (t+\delta )H}\psi$. We have $\Vert [-\Delta ,x^m]\phi _t^\delta \Vert \leq \sum _{i=1}^d [m(m-1)\Vert x_i^{m-2}\phi _t^\delta \Vert + 2m\Vert x_i^{m-1}\partial _{x_i}\phi _t^\delta \Vert ]$. The calculations (A.16)–(A.19) and their later generalization to all m imply that we may bound the second term by $C\Vert x^m\phi _t^{\delta }\Vert ^{1-\frac {1}{m}}\Vert D^m\phi _t^{\delta }\Vert ^{\frac {1}{m}}$. The norm $\Vert x^p\phi _t^{\delta }\Vert \to 0$ as $\delta \to 0$ for $p=m-2,m$ using the analog of (A.12), while $\Vert D^m\phi _t^\delta \Vert$ is controlled using (A.15). Finally the last term in (A.13) is controlled using the same Fatou argument and we get (A.22). □