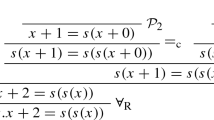Keywords

1 Introduction

Although clausal proof techniques have enjoyed success in automated theorem proving, some applications benefit from reasoning on unaltered formulas (rather than Skolemized clauses), while others require the production of proofs in a sequent calculus. These roles are fulfilled by provers based on the tableau method [17], as initially designed by Beth and Hintikka [2, 13]. For first-order logic, efficient handling of universal formulas is typically achieved with free variables that are instantiated only when needed to close a branch. This step is said to be destructive because it may affect open branches sharing variables. This causes fairness (and consequently, completeness) issues, as illustrated in Fig. 1. In this example, exploring the left branch produces a substitution that prevents direct closure of the right branch. Reintroducing the original quantified formula with a different free variable is not sufficient to close the right branch, because an applicable \(\delta \)-rule creates a new Skolem symbol that will result in a different but equally problematic substitution every time a left branch is explored. Thus, systematically exploring the left branch before the right leads to non-termination of the search. Conversely, exploring the right branch first produces a substitution (which instantiates the free variable X with a rather than b) that closes both branches.

Fig. 1.
figure 1

Incompleteness caused by unfair selection of branches

Full size image

Concurrent computing offers a way to implement a proof search procedure that explores branches simultaneously. Such a procedure can compare closing substitutions to detect (dis)agreements between branches, and consequently either close branches early, or restart proof attempts with limited backtracking. The simultaneous exploration of branches is handled by the concurrency system, either by interleaving computations through scheduling, or by executing tasks in parallel if the hardware resources allow it. A concurrent procedure naturally lends itself to parallel execution, allowing us to take advantage of multi-core architectures for efficient first-order theorem proving. Thus, concurrency provides an elegant and efficient solution to proof search with free variable tableaux.

In this paper, we describe a concurrent destructive proof search procedure for first-order analytic tableaux (Sect. 2) and its implementation in a tool called Goéland, as well as its evaluation on problems from the TPTP library [19] and comparison to other state-of-the-art provers (Sect. 3).

Related Work. A lot of research has been carried out on the parallelization of proof search procedures [4], often focusing primarily on parallel execution and performance. In contrast, we use concurrency not only as a way to take advantage of multi-core architectures, but also as an algorithmic device that is useful even for sequential execution (with interleaved threads). Some concurrent and parallel approaches focus more distinctly on the exploration of the search space, either by dividing the search space between processes (distributed search) or by using processes with different search plans on the same space (multi search) [3]. These approaches can be performed either by heterogeneous systems that rely on cooperation between systems with different inference systems [1, 8, 12], or homogeneous systems where all deductive processes use the same inference system. According to this classification, the technique presented here is a homogeneous system that performs a distributed search. Concurrent tableaux provers include the model-elimination provers CPTheo [12] and Partheo [18], and the higher-order prover Hot [15], which notably uses concurrency to deal with fairness issues arising from the non-terminating nature of higher-order unification. Lastly, concurrency has been used as the basis of a generic framework to present various proof strategies [10] or allow distributed calculations over a network [21].

2 Concurrent Proof Search

Free Variable Tableaux. Goéland attempts to build a refutation proof for a first-order formula, i.e., a closed tableau for its negation, using a standard free-variable tableau calculus [11]. The calculus is composed of \(\alpha \)-, \(\gamma \)- and \(\delta \)-rules that extend a branch with one formula, \(\beta \)-rules that divide a branch by extending it with two formulas, and a \(\odot \)-rule that closes a branch. \(\gamma \)-rules deal with universally-quantified formulas by introducing a formula with a free variable. A free variable is not universally quantified, but is instead a placeholder for some term instantiation, typically determined upon branch closure. \(\delta \)-rules deal with existentially-quantified formulas by introducing a formula with a Skolem function symbol that takes as arguments the free variables in the branch. This ensures freshness of the Skolem symbol independently of variable instantiation.

The branch closure rule applies to a branch carrying atomic formulas P and Q such that, for some substitution \(\sigma \), \(\sigma (P)\) = \(\sigma (\lnot {}Q)\). In that case, \(\sigma \) is applied to all branches. That rule is consequently destructive: applying a substitution to close one branch may modify another, removing the possibility to close it immediately. A tableau is closed when all its branches are closed. Closing a tableau can thus be seen as providing a global unifier that closes all branches.

Semantics for Concurrency. Goéland relies on a concurrent search procedure. In order to present this procedure, we use a simple While language augmented with instructions for concurrency, in the style of CSP [14]. Each process has its own variable store, as well as a collection of process identifiers used for communication: \(\pi _\text {parent}\) denotes the identifier of a process’s parent, while \(\varPi _\text {children}\) denotes the collection of identifiers of active children of that process. Given a process identifier \(\pi \) and an expression e, the command \(\pi {{\,\mathrm{\boldsymbol{!}}\,}}e\) is used to send an asynchronous message with the value e to the process identified by \(\pi \). Conversely, the command \(\pi {{\,\mathrm{\boldsymbol{?}}\,}}x\) blocks the execution until the process identified by \(\pi \) sends a message, which is stored in the variable x. Lastly, the instruction start creates a new process that executes a function with some given arguments, while the instruction kill interrupts the execution of a process according to its identifier.

Proof Search Procedure. The proof search is carried out concurrently by processes corresponding to branches of the tableau. Processes are started upon application of a \(\beta \)-rule, one for each new branch. Communications between processes take two forms: a process may send a set of closing substitutions for its branch to its parent, or a parent may send a substitution (that closes one of its children’s branch) to the other children. The proof search is performed by the \(proofSearch\), \(waitForParent\), and \(waitForChildren\) procedures (described in Procedures 1, 2, and 3, respectively).

The \(proofSearch\) procedure initiates the proof search for a branch. It first attempts to apply the closure rule. A closing substitution is called local to a process if its domain includes only free variables introduced by this process or one of its descendants (i.e., if the variables do not occur higher in the proof tree). If one of the closing substitutions is local to the process, it is reported and the process terminates. If only non-local closing substitutions are found, they are reported and the process executes \(waitForParent\). Otherwise, the procedure applies tableau expansion rules according to the priority: \(\alpha \prec \delta \prec \beta \prec \gamma \). If a \(\beta \)-rule is applied, new processes are started, and each of them executes \(proofSearch\) on the newly created branch, while the current process executes \(waitForChildren\).

figure a

The \(waitForParent\) procedure is executed by a process after it has found closing non-local substitutions. Such substitutions may prevent closure in other branches. In these cases, the parent will eventually send another candidate substitution. \(waitForParent\) waits until such a substitution is received, and triggers a new step of proof search. The process may also be terminated by its parent (via the kill instruction) during the execution of this procedure, if one of the substitutions previously sent by the process leads to closing the parent’s branch.

figure b

The \(waitForChildren\) procedure is executed by a process after the application of a \(\beta \)-rule and the creation of child processes. The set of substitutions sent by each child is stored in a map \( subst \) (Line 2), initially undefined everywhere (\({{\,\mathrm{f_\bot }\,}}\)). This procedure closes the branch (Line 13) if there exists a substitution \(\theta \) that agrees with one closing substitution of each child process, i.e., for each child process, the process has reported a substitution \(\sigma \) such that \(\sigma (X) = \theta (X)\) for any variable X in the domain of \(\sigma \). If no such substitution can be found after all the children have closed their branches, then one closing substitution \(\sigma \in subst \) is picked arbitrarily (Line 18) and sent to all the children (which are at that point executing \(waitForParent\)) to restart their proof attempts. With the additional constraint of the substitution \(\sigma \), the new proof attempts may fail, hence the necessity for backtracking among candidate substitutions \({{\,\mathrm{\Theta _\text {backtrack}}\,}}\) (Line 5 and 6). At the end, if all the substitutions were tried and failed, the process sends a failure message (symbolized by \(\emptyset \)) to its parent.

figure c

Thus, concurrency and backtracking are used to prevent incompleteness resulting from unfair instantiation of free variables. Another potential source of unfairness is the \(\gamma \)-rule, when applied more than once to a universal formula (reintroduction). This may be needed to find a refutation, but unbounded reintroductions would lead to unfairness. Iterative deepening [16] is used to guard against this: a bound limits the number of reintroductions on any single branch, and if no proof is found, the bound is increased and the proof search restarted.

Figure 2 illustrates the interactions between processes for the problem in Fig. 1, and shows how concurrency helps ensure fairness. It describes the parent process, in the top box, and below, the two children processes created upon application of the \(\beta \)-rule. Dotted lines separate successive states of a process (i.e., Procedures 1, 2 and 3 seen above), while arrows and boxes represent substitution exchanges. The number above each arrow indicates the chronology of the interactions. After both children have returned a substitution (1), the parent arbitrarily chooses one of them, starting with \(X \mapsto b\), and sends it to the children (2). Since this substitution prevents closure in the right branch (3), the parent later backtracks and sends the other substitution \(X \mapsto a\) (4), allowing both children (5) and then the parent to close successfully.

Fig. 2.
figure 2

Proof search and resulting proof for \(P(a)\wedge \lnot {}P(b)\wedge \forall {}x.(P(x)\Leftrightarrow \forall {}y.P(y))\)

Full size image

3 Implementation and Experimental Results

Implementation. The procedures presented in Sect. 2 are implemented in the Goéland proverFootnote 1 using the Go language. Go supports concurrency and parallelism, based on lightweight execution threads called goroutines [20]. Goroutines are executed according to a so-called hybrid threading (or M : N) model: M goroutines are executed over N effective threads and scheduling is managed by both the Go runtime and the operating system. This threading model allows the execution of a large number of goroutines with a reasonable consumption of system resources. Goroutines use channels to exchange messages, so that the implementation is close to the presentation of Sect. 2.

Goéland has, for the time being, no dedicated mechanism for equality reasoning. However, we have implemented an extension that implements deduction modulo theory [9], i.e., transforms axioms into rewrite rules over propositions and terms. Deduction modulo theory has proved very useful to improve proof search when integrated into usual automated proof techniques [5], and also produces excellent results with manually-defined rewrite rules [6, 7]. In Goéland, deduction modulo theory selects some axioms on the basis of a simple syntactic criterion and replaces them by rewrite rules.

Experimental Results. We evaluated Goéland on two problems categories with FOF theorems in the TPTP library (v7.4.0): syntactic problems without equality (SYN) and problems of set theory (SET). The former was chosen for its elementary nature, whereas the latter was picked primarily to evaluate the performance of the deduction modulo theory, as the axioms of set theory are good targets for rewriting. We compared the results with those of five other provers: tableau-based provers Zenon (v0.8.5), Princess (v2021-05-10) and LeoIII (v1.6), as well as saturation-based provers E (v2.6) and Vampire (v4.6.1). Experiments were executed on a computer equipped with an Intel Xeon E5-2680 v4 2.4GHz 2 \(\mathsf {\times }\) 14-core processor and 128 GB of memory. Each proof attempt was limited to 300 s. Table 1 and Fig. 3 report the results. Table 1 shows the number of problems solved by each prover, the cumulative time, and the number of problems solved by a given prover but not by Goéland (\(+\)) and conversely (−). Figure 3 presents the cumulative time required to solve the number of problems.

As can be observed, the results of Goéland are comparable to, or slightly better than those of other tableau-based provers on problems from SYN, while saturation theorem provers achieve the best results. On this category, the axioms do not trigger deduction modulo theory rewriting rules, hence the similar results of Goéland and Goéland+DMT. On SET, Goéland+DMT obtains significantly better results than other tableau-based provers. This confirms the previous results on the performance of deduction modulo theory for set theory [6, 7].

Table 1. Experimental results over the TPTP library
Full size table
Fig. 3.
figure 3

Cumulative time per problem solved between Goéland, Goéland+DMT(GDMT), Zenon, Princess, LeoIII, E, and Vampire

Full size image

4 Conclusion

We have presented a concurrent proof search procedure for tableaux in first-order logic with the aim of ensuring a fair exploration of the search space. This procedure has been implemented in the prover Goéland. This tool is still in an early stage, and (with the exception of deduction modulo theory) implements only the most basic functionalities, yet empirical results are encouraging. We plan on adding functionalities such as equality reasoning, arithmetic reasoning, and support for polymorphism to Goéland, which should increase its usability and performance. The integration of these functionalities in the context of a concurrent prover seems to be a promising line of research. Further investigation is also needed to prove the fairness, and therefore completeness, of our procedure.