Abstract
We consider the concept and applications of random vectors in this chapter. In describing the probabilistic properties of a random vector, we need to specify not only the probabilistic properties of each of the element random variables, but also the relationships among random variables.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
The multinomial pmf is discussed also in Appendix 4.1.
- 2.
Here, the events ‘2 occurs \(k-1\) times’ for \(k=0\) and ‘4 or 6 occurs \(9-k\) times’ for \(k=10\) are both empty events and thus have probability 0, which can be confirmed from \((-1)! \rightarrow \pm \infty \).
- 3.
Considering \(\{(x,\theta ): \, x<a \sin \theta \} = \left\{ (x,\theta ): \, 0 \le x \le a, ~\sin^{-1}\frac{x}{a} \le \theta < \frac{\pi }{2} \right\} \), the result (4.1.60) can be obtained also as \( P_B = \frac{2}{\pi b}\int _{0}^{a} \int _{\sin^{-1}\frac{x}{a}}^{\frac{\pi }{2}} d\theta dx = \frac{2}{\pi b}\int _{0}^{a} \left( \frac{\pi }{2} - \sin {-1}\frac{x}{a} \right) dx = \frac{a}{b} - \frac{2}{\pi b}\int _{0}^{a} \sin^{-1}\frac{x}{a} dx = \frac{a}{b} - \frac{2a}{\pi b}\int _{0}^{ \frac{\pi }{2}} t \cos t dt = \left. \frac{a}{b} - \frac{2a}{\pi b} (t \sin t + \cos t) \right| _{t=0}^{ \frac{\pi }{2}} = \frac{2a}{\pi b}\).
- 4.
The Jacobian is also referred to as the transformation Jacobian or Jacobian determinant. In addition, from the property of determinant, we also have \(J\left( \boldsymbol{g}(\boldsymbol{x})\right) =\left| \begin{array} {cccc} \frac{\partial g_1}{\partial x_1} &{} \frac{\partial g_2}{\partial x_1} &{} \cdots &{} \frac{\partial g_n}{\partial x_1}\\ \frac{\partial g_1}{\partial x_2} &{} \frac{\partial g_2}{\partial x_2} &{} \cdots &{} \frac{\partial g_n}{\partial x_2}\\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ \frac{\partial g_1}{\partial x_n} &{} \frac{\partial g_2}{\partial x_n} &{} \cdots &{} \frac{\partial g_n}{\partial x_n} \end{array} \right| \).
- 5.
More specifically, we have \( f_{X_1}\left( x_1 \right) = \int _{-\infty }^{\infty } f_{X_1,X_2}\left( x_1, x_2 \right) dx_2 = \int _{-\infty }^{\infty } 24x_1\left( 1 - x_2 \right) u\left( x_2 - x_1 \right) u\left( 1 - x_2 \right) dx_2 u\left( x_1 \right) = \int _{x_1}^{1}24x_1\left( 1 - x_2 \right) dx_2 \, u\left( x_1 \right) u\left( 1 - x_1 \right) = 12 x_1 \left( 1 - x_1 \right)^2 u\left( x_1 \right) u\left( 1 - x_1 \right) \).
- 6.
More specifically, we have \(f_{X_2}\left( x_2 \right) = \int _{-\infty }^{\infty } f_{X_1,X_2}\left( x_1, x_2 \right) dx_1 = \int _{-\infty }^{\infty } 24x_1\left( 1 - x_2 \right) u\left( x_1 \right) u\left( x_2 - x_1 \right) dx_1 u\left( 1 - x_2 \right) = \int _{0}^{x_2}24x_1\left( 1 - x_2 \right) dx_1 u\left( x_2 \right) u\left( 1 - x_2 \right) = 12x_2^2(1 - x_2) u\left( x_2 \right) u\left( 1 - x_2 \right) \).
- 7.
Because \(u\left( y_1- y_2 \right) u\left( 2y_2 - y_1 \right) \) is non-zero only when \(\left\{ \left( y_1, y_2 \right) : y_2< y_1< 2y_2 \right\} = \left\{ y_1: \, y_2< y_1 < 2y_2 \right\} \cap \left\{ y_2: \, y_2 >0 \right\} \), we have \(f_{Y_2}\left( y_2 \right) = \int _{-\infty }^{\infty } 24\left( y_1- y_2 \right) \left( 1-y_2 \right) u\left( y_1-y_2 \right) u\left( 2y_2 - y_1 \right) u\left( 1-y_2 \right) dy_1 = \left( 1-y_2 \right) \int _{y_2}^{2y_2} 24\left( y_1-y_2 \right) u\left( 1-y_2 \right) u\left( y_2 \right) dy_1 = 24\left( 1-y_2 \right) \left[ \frac{1}{2} y_1^2- y_2y_1\right] _{y_2}^{2y_2} u\left( 1-y_2 \right) u\left( y_2 \right) = 12\left( 1-y_2 \right) y_2^2 u\left( 1-y_2 \right) u\left( y_2 \right) \), which is the same as (4.2.17): note that we have chosen \(Y_2 = X_2\).
- 8.
Conditional distribution in random vectors will be discussed in Sect. 4.4 in more detail.
- 9.
If the order of integration is interchanged, then
 will become
will become  .
. - 10.
Here,
 , for example, can more specifically be written as
, for example, can more specifically be written as  .
. - 11.
The expected values of
 and
and  can of course be obtained with the pmf’s of
can of course be obtained with the pmf’s of  and
and 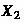 obtained already in Example 4.1.11.
obtained already in Example 4.1.11. - 12.
When there is more than one subscript, we need commas in some cases: for example, the joint pdf
 of
of  should be differentiated from the pdf
should be differentiated from the pdf  of the product XY. In other cases, we do not need to use commas: for instance,
of the product XY. In other cases, we do not need to use commas: for instance,  ,
,  ,
,  denote relations among two or more random variables and thus is expressed without any comma.
denote relations among two or more random variables and thus is expressed without any comma. - 13.
A matrix
 such that
such that  is called Hermitian.
is called Hermitian. - 14.
A matrix
 such that
such that  is normal.
is normal. - 15.
A matrix
 is unitary if
is unitary if  or if
or if  . In the real space, a unitary matrix is referred to as an orthogonal matrix. A Hermitian matrix is always a normal matrix and a unitary matrix is always a normal matrix, but the converses are not necessarily true: for example,
. In the real space, a unitary matrix is referred to as an orthogonal matrix. A Hermitian matrix is always a normal matrix and a unitary matrix is always a normal matrix, but the converses are not necessarily true: for example,  is normal, but is neither Hermitian nor unitary.
is normal, but is neither Hermitian nor unitary. - 16.
As in other cases, the conditional joint cdf is also referred to as the conditional cdf if it does not cause any ambiguity.
- 17.
The conditional joint pdf is also referred to as the conditional pdf if it does not cause any ambiguity.
- 18.
Here,
 .
. - 19.
More generally, we can interpret ‘appropriate x’ as ‘any x such that \(\left( i_1, i_2, \ldots , i_n, x \right) \) is a non-overlap** pattern’, and x can be chosen even if it is not a realization of any \(X_k\). For example, when \(p_{1} + p_2 + p_3 = 1\), we could choose \(x=7\).
References
M. Abramowitz, I.A. Stegun (eds.), Handbook of Mathematical Functions (Dover, New York, 1972)
J. Bae, H. Kwon, S.R. Park, J. Lee, I. Song, Explicit correlation coefficients among random variables, ranks, and magnitude ranks. IEEE Trans. Inform. Theory 52(5), 2233–2240 (2006)
N. Balakrishnan, Handbook of the Logistic Distribution (Marcel Dekker, New York, 1992)
D.L. Burdick, A note on symmetric random variables. Ann. Math. Stat. 43(6), 2039–2040 (1972)
W.B. Davenport Jr., Probability and Random Processes (McGraw-Hill, New York, 1970)
H.A. David, H.N. Nagaraja, Order Statistics, 3rd edn. (Wiley, New York, 2003)
A.P. Dawid, Some misleading arguments involving conditional independence. J. R. Stat. Soc. Ser. B (Methodological) 41(2), 249–252 (1979)
W.A. Gardner, Introduction to Random Processes with Applications to Signals and Systems, 2nd edn. (McGraw-Hill, New York, 1990)
S. Geisser, N. Mantel, Pairwise independence of jointly dependent variables. Ann. Math. Stat. 33(1), 290–291 (1962)
R.M. Gray, L.D. Davisson, An Introduction to Statistical Signal Processing (Cambridge University Press, Cambridge, 2010)
R.A. Horn, C.R. Johnson, Matrix Analysis (Cambridge University Press, Cambridge, 1985)
N.L. Johnson, S. Kotz, Distributions in Statistics: Continuous Multivariate Distributions (Wiley, New York, 1972)
S.A. Kassam, Signal Detection in Non-Gaussian Noise (Springer, New York, 1988)
S.M. Kendall, A. Stuart, Advanced Theory of Statistics, vol. II (Oxford University, New York, 1979)
A. Leon-Garcia, Probability, Statistics, and Random Processes for Electrical Engineering, 3rd edn. (Prentice Hall, New York, 2008)
K.V. Mardia, Families of Bivariate Distributions (Charles Griffin and Company, London, 1970)
R.N. McDonough, A.D. Whalen, Detection of Signals in Noise, 2nd edn. (Academic, New York, 1995)
P.T. Nielsen, On the expected duration of a search for a fixed pattern in random data. IEEE Trans. Inform. Theory 19(5), 702–704 (1973)
A. Papoulis, S.U. Pillai, Probability, Random Variables, and Stochastic Processes, 4th edn. (McGraw-Hill, New York, 2002)
V.K. Rohatgi, A.KMd.E. Saleh, An Introduction to Probability and Statistics, 2nd edn. (Wiley, New York, 2001)
J.P. Romano, A.F. Siegel, Counterexamples in Probability and Statistics (Chapman and Hall, New York, 1986)
S.M. Ross, A First Course in Probability (Macmillan, New York, 1976)
S.M. Ross, Stochastic Processes, 2nd edn. (Wiley, New York, 1996)
S.M. Ross, Introduction to Probability Models, 10th edn. (Academic, Boston, 2009)
G. Samorodnitsky, M.S. Taqqu, Non-Gaussian Random Processes: Stochastic Models with Infinite Variance (Chapman and Hall, New York, 1994)
I. Song, J. Bae, S.Y. Kim, Advanced Theory of Signal Detection (Springer, Berlin, 2002)
J.M. Stoyanov, Counterexamples in Probability, 3rd edn. (Dover, New York, 2013)
A. Stuart and J. K. Ord, Advanced Theory of Statistics: Vol. 1. Distribution Theory, 5th edn. (Oxford University, New York, 1987)
J.B. Thomas, Introduction to Probability (Springer, New York, 1986)
Y.H. Wang, Dependent random variables with independent subsets. Am. Math. Mon. 86(4), 290–292 (1979).
G.L. Wies, E.B. Hall, Counterexamples in Probability and Real Analysis (Oxford University, New York, 1993)
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendices
4.1.1 Appendix 4.1 Multinomial Random Variables
Let us discuss in more detail the multinomial random variables introduced in Example 4.1.4.
Definition 4.A.1
(multinomial distribution) Assume n repetitions of an independent experiment of which the outcomes are a collection  of disjoint events with probability
of disjoint events with probability  , where
, where  . Denote by
. Denote by  the number of occurrences of event
the number of occurrences of event  . Then, the joint distribution of
. Then, the joint distribution of  is called the multinomial distribution, and the joint pmf of
is called the multinomial distribution, and the joint pmf of  is
is
for  and
and  .
.
The right-hand side of (4.A.1) is the coefficient of  in the multinomial expansion of
in the multinomial expansion of  .
.
Example 4.A.1
In a repetition of rolling of a fair die ten times, let  be the numbers of
be the numbers of  ,
,  , and
, and  , respectively. Then, the joint pmf of
, respectively. Then, the joint pmf of  is
is
for  such that
such that  . Based on this pmf, the probability of the event
. Based on this pmf, the probability of the event  can be obtained as
can be obtained as  .
. 
Example 4.A.2
As in the binomial distribution, let us consider the approximation of the multinomial distribution in terms of the Poisson distribution. For  and
and  when
when  , we have
, we have  ,
,  , and
, and  , where
, where  . Based on these results, we can show that
. Based on these results, we can show that  , i.e.,
, i.e.,
The result (4.A.3) with  is clearly the same as (3.5.19) obtained in Theorem 3.5.2 for the binomial distribution.
is clearly the same as (3.5.19) obtained in Theorem 3.5.2 for the binomial distribution. 
Example 4.A.3
For  and
and  , the multinomial pmf can be approximated as
, the multinomial pmf can be approximated as
Consider the case of \(r=2\) in (4.A.4). Letting  ,
,  ,
,  , and
, and  , we get
, we get  as
as
which is the same as (3.5.16) of Theorem 3.5.1 for the binomial distribution. 
The multinomial distribution (Johnson and Kotz 1972) is a generalization of the binomial distribution, and the special case \(r=2\) of the multinomial distribution is the binomial distribution. For the multinomial random vector  , the marginal distribution of
, the marginal distribution of  is a binomial distribution. In addition, assuming
is a binomial distribution. In addition, assuming  as the \((s+1)\)-st random variable, the distribution of the subvector
as the \((s+1)\)-st random variable, the distribution of the subvector  of
of  is also a multinomial distribution with the joint pmf
is also a multinomial distribution with the joint pmf
Letting  in (4.A.6), we get the binomial pmf
in (4.A.6), we get the binomial pmf  .
.
In addition, when a subvector of  is given, the conditional joint distribution of the random vector of the remaining random variables is also a multinomial distribution, which depends not on the individual remaining random variables but on the sum of the remaining random variables. For example, assume
is given, the conditional joint distribution of the random vector of the remaining random variables is also a multinomial distribution, which depends not on the individual remaining random variables but on the sum of the remaining random variables. For example, assume  . Then, the joint distribution of
. Then, the joint distribution of  when
when  is given is a multinomial distribution, which depends not on
is given is a multinomial distribution, which depends not on  and
and  individually but on the sum
individually but on the sum  .
.
Finally, when \(\boldsymbol{X}= \left( X_1, X_2, \ldots , X_r \right) \) has the pmf (4.A.1), it is known that
where i is not equal to any of \(\left\{ b_j\right\} _{j=1}^{r-1}\). It is also known that we have the conditional expected value
the correlation coefficient
and \(\mathsf{Cov}\left( X_i, X_j \right) = -n p_i p_j \) for \(X_i\) and \(X_j\) with \( i \ne j \).
4.1.2 Appendix 4.2 Mean Time to Pattern
Denote by \(X_k\) the outcome of the k-th trial of an experiment with the pmf
for \(j=1 ,2 , \ldots \), where \(\sum \limits _{j=1}^{\infty } p_j =1\). The number of trials of the experiment until a pattern \(M=\left( i_1, i_2, \ldots , i_n \right) \) is observed for the first time is called the time to pattern M, which is denoted by \(T=T(M)=T\left( i_1, i_2, \ldots , i_n \right) \). For example, when the sequence of the outcomes is \((6, 4, 9, 5, 5, \mathbf{9, 5, 7}, 3, 2, \ldots )\), the time to pattern (9, 5, 7) is \(T(9, 5, 7)=8\). Now, let us obtain (Nielsen 1973) the mean time \(\mathsf{E}\{T (M)\}\) for the pattern M.
First, when M satisfies
for \(n =2, 3, \ldots \) and \(k=1, 2, \ldots , n-1\), the pattern M overlaps and \(L_k = \left( i_1, i_2, \ldots , i_k \right) \) is an overlap** piece or a bifix of M. For instance, \((\text{ A, } \text{ B, } \text{ C})\), \((\text{ D, } \text{ E, } \text{ F, } \text{ G})\), \((\text{ S, } \text{ S, } \text{ P})\), (4, 4, 5), and (4, 1, 3, 3, 2) are non-overlap** patterns; and \((\text{ A, } \text{ B, } \text{ G, } \text{ A, } \text{ B})\), \((\text{9, } \text{9, } \text{2, } \text{4, } \text{9, } \text{9 })\), (3, 4, 3), (5, 4, 5, 4, 5), and (5, 4, 5, 4, 5, 4) are overlap** patterns. Note that the length k of an overlap** piece can be longer than \(\frac{n}{2}\) and that more than one overlap** pieces may exist in a pattern as in (5, 4, 5, 4, 5) and (5, 4, 5, 4, 5, 4). In addition, when the overlap** piece is of length k, the elements in the pattern are the same at every other \(n-k-1\): for instance, \(M=\left( i_1, i_1, \ldots , i_1 \right) \) when \(k=n-1\). A non-overlap** pattern can be regarded as an overlap** pattern with \(k=n\).
4.1.3 (A) A Recursive Method
First, the mean time \(\mathsf{E}\{T \left( i_1 \right) \} = \sum \limits _{k=1}^{\infty } k \mathsf{P}(T \left( i_1 \right) = k) = \sum \limits _{k=1}^{\infty } k \left( 1-p_{i_1} \right)^{k-1} p_{i_1} \) to pattern \(i_1\) of length 1 is
When M has J overlap** pieces, let the lengths of the overlap** pieces be \(K_0< K_1< \cdots< K_J < K_{J+1}\) with \(K_0 = 0\) and \(K_{J+1} = n\), and express M as \(M =\left( i_1, i_2, \ldots , i_{K_1}, i_{K_1+1}, \ldots , i_{K_2}, i_{K_2+1}, \ldots , i_{K_J}, i_{K_J+1}, \ldots , i_{n-1}, i_n \right) \). If we write the overlap** pieces \(\left\{ L_{K_j} = \left( i_1, i_2, \ldots , i_{K_j} \right) \right\} _{j=1}^{J}\) as
where \(K_{\alpha , \beta }= K_{\alpha } -K_{\beta }\), then we have \(i_m = i_{K_{b,a} +m}\) for \(1 \le a \le b \le J\) and \(m=1, 2, \ldots , K_a - K_{a-1}\) because the values at the same column in (4.A.13) are all the same.
Denote by \(T \left( A_1 \right) \) the time to wait until the occurrence of \(M_{+1}= \left( i_1, i_2, \ldots , i_{n}, i_{n+1} \right) \) after the occurrence of M. Then, we have
because \(T \left( M_{+1} \right) = T(M ) +T \left( A_1 \right) \). Here, we can express \(\mathsf{E}\left\{ T \left( A_1 \right) \right\} \) as
Let us focus on the term \(\mathsf{E}\left\{ T \left. \left( A_1 \right) \right| X_{n+1} =x\right\} \) in (4.A.15). First, when \(x=i_{K_j +1}\) for example, denote by \(\tilde{L}_{K_j +1} = \left( i_1, i_2, \ldots , i_{K_j}, i_{K_j +1} \right) \) the j-th overlap** piece with its immediate next element, and recollect (4.A.11). Then, we have
from which we can get \(\mathsf{E}\left\{ T \left( A_1 \right) \left| X_{n+1} =i_{K_j+1} \right. \right\} = 1+ \mathsf{E}\left\{ T \left( M_{+1} \right) \left| \tilde{L}_{K_j +1} \right. \right\} \). We can similarly get
when \(i_1=i_{K_0 +1}\), \(i_{K_1 +1}\), \(\ldots \), \(i_{K_J +1}\), \(i_{K_{J+1} +1} = i_{n +1}\) are all distinct. Here, recollecting
from \(\mathsf{E}\left\{ T \left( M_{+1} \right) \right\} = \mathsf{E}\left\{ T \left( M_{+1} \right) \left| \tilde{L}_{K_j +1} \right. \right\} + \mathsf{E}\left\{ T\left( \tilde{L}_{K_j +1} \right) \right\} \), we get
from (4.A.14), (4.A.15), and (4.A.17). We can rewrite (4.A.19) as
after some steps.
Let us next consider the case in which some are the same among \(i_{K_0 +1}\), \(i_{K_1 +1}\), \(\ldots \), \(i_{K_J +1}\), and \(i_{n +1}\). For example, assume \(a < b\) and \(i_{K_a +1}=i_{K_b +1}\). Then, for \(x=i_{K_a +1} =i_{K_b +1}\) in (4.A.15) and (4.A.17), the line ‘\(1+ \mathsf{E}\left\{ T \left( M_{+1} \right) \left| \tilde{L}_{K_a +1} \right. \right\} , x = i_{K_a +1}\)’ corresponding to the \(K_a\)-th piece among the lines of (4.A.17) will disappear because the longest overlap** piece in the last part of \(M_{+1}\) is not \(\tilde{L}_{K_a +1}\) but \(\tilde{L}_{K_b +1}\), Based on this fact, if we follow steps similar to those leading to (4.A.19) and (4.A.20), we get
where \(\sum \limits _{j}\) denotes the sum from \(j=0\) to J letting all \(\mathsf{E}\left\{ T\left( \tilde{L}_{K_a +1} \right) \right\} \) to 0 when \(i_{K_a +1}= i_{K_b +1}\) for \(0 \le a < b \le J+1\). Note here that \(\left\{ K_j \right\} _{j=1}^J\) are the lengths of the overlap** pieces of M, not of \(M_{+1}\). Note also that (4.A.20) is a special case of (4.A.21): in other words, (4.A.21) is always applicable.
In essence, starting from \(\mathsf{E}\left\{ T \left( i_1 \right) \right\} = \frac{1}{ p_{i_{1}}} \) shown in (4.A.12), we can successively obtain \(\mathsf{E}\left\{ T \left( i_1 , i_2 \right) \right\} \), \(\mathsf{E}\left\{ T \left( i_1, i_2, i_3 \right) \right\} \), \(\ldots \), \(\mathsf{E}\{T(M)\}\) based on (4.A.21).
Example 4.A.4
For an i.i.d. random variables \(\left\{ X_k \right\} _{k=1}^{\infty }\) with the marginal pmf \(p_{X_k} (j) = p_j\), obtain the mean time to \(M=(5, 4, 5, 3)\).
Solution
First, \(\mathsf{E}\{T(5)\} = \frac{1}{p_5}\). When (5, 4) is \(M_{+1}\), because \(J=0\), \(i_{K_0 +1}=5\), and \(i_{n+1}=4\), we get
i.e., \(\mathsf{E}\{T(5,4)\} = \frac{1}{p_4} \left[ \mathsf{E}\{T(5)\} + 1 - p_5 \mathsf{E}\{T(5)\}\right] = \frac{1}{p_4 p_5}\). Next, when (5, 4, 5) is \(M_{+1}\), because \(J=0\) and \(i_{K_0 +1}=5=i_{n+1}\), we get \(\sum \limits _{j} p_{i_{K_j +1}} \mathsf{E}\left\{ T\left( \tilde{L}_{K_j +1} \right) \right\} = 0\). Thus, \(\mathsf{E}\{T(5,4,5)\} = \frac{1}{p_5} \left[ \mathsf{E}\{T(5,4)\} +1 \right] = \frac{1}{p_4 p_5^2} + \frac{1}{p_5}\). Finally, when (5, 4, 5, 3) is \(M_{+1}\), because \(J=1\) and \(K_1=1\), we have \(i_{K_0 +1}=i_1=5\), \(i_{K_1 +1}=i_2=4\), \(i_{K_{J+1} +1}=i_4=3\), and
i.e., \(\mathsf{E}\{T(5,4,5,3)\} = \frac{1}{p_3} \left[ \mathsf{E}\{T(5,4,5)\} + 1 - p_5 \mathsf{E}\{T(5)\} - p_4 \mathsf{E}\{T(5,4)\} \right] = \frac{1}{p_3 p_4 p_5^2}\). 
4.1.4 (B) An Efficient Method
The result (4.A.21) is applicable always. However, as we have observed in Example 4.A.4, (4.A.21) possesses some inefficiency in the sense that we have to first obtain the expected values \(\mathsf{E}\left\{ \left( i_1\right) \right\} \), \(\mathsf{E}\left\{ \left( i_1, i_2 \right) \right\} \), \(\ldots \), \(\mathsf{E}\left\{ \left( i_1, i_2, \ldots , i_{n-1} \right) \right\} \) before we can obtain the expected value \(\mathsf{E}\left\{ \left( i_1, i_2, \ldots , i_n \right) \right\} \). Let us now consider a more efficient method.
4.1.5 (B-1) Non-overlap** Patterns
When the pattern M is non-overlap**, we have
for every \(k \in \{1, 2, \ldots , n-1\}\). Based on this observation, let us show that
First, when \(T = j+n\), the first occurrence of M is \(\left( X_{j+1}, X_{j+2}, \ldots , X_{j+n} \right) \), which implies that \(T>j\) and
Next, let us show that \(T=j+n\) when \(T > j\) and (4.A.26) holds true. If \(k \in \{1, 2, \ldots , n-1\}\) and \(T=j+k\), then we have \(X_{j+k} =i_n, X_{j+k-1}=i_{n-1}, \ldots , X_{j+1}=i_{n-k+1}\). This is a contradiction to \(\left( X_{j+1}, X_{j+2}, \ldots , X_{j+n} \right) = \left( i_1, i_2, \ldots , i_k \right) \ne \left( i_{n-k+1}, i_{n-k+2}, \ldots , i_n \right) \) implied by (4.A.24) and (4.A.26). In short, for any value k in \(\{1, 2, \ldots , n-1\}\), we have \(T \ne j+k\) and thus \(T \ge j+n\). Meanwhile, (4.A.26) implies \(T \le j+n\). Thus, we get \(T = j+n\).
From (4.A.25), we have
Here, the event \(T> j\) is dependent only on \(X_1, X_2, \ldots , X_j\) but not on \(X_{j+1}, X_{j+2}, \ldots , X_{j+n}\), and thus
where \(\hat{p} = p_{i_1}p_{i_2}\cdots p_{i_n}\). Now, recollecting that \(\sum \limits _{j=0}^{\infty } \mathsf{P}(T = j+n) = 1\) and that \(\sum \limits _{j=0}^{\infty } \mathsf{P}(T> j) = \mathsf{P}(T> 0) + \mathsf{P}(T > 1) + \cdots = \left[ \mathsf{P}(T =1 ) + \mathsf{P}(T =2 ) + \cdots \right] + \left[ \mathsf{P}(T =2 ) + \mathsf{P}(T =3 ) + \cdots \right] + \cdots = \sum \limits _{j=0}^{\infty } j \, \mathsf{P}(T = j)\), i.e.,
we get \(\hat{p} \sum \limits _{j=0}^{\infty } \mathsf{P}(T > j) = \hat{p} \mathsf{E}\{T\} = 1\) from (4.A.28). Thus, we have \(\mathsf{E}\{T(M)\} = \frac{1}{\hat{p}}\), i.e.,
Example 4.A.5
For the pattern \(M=(9, 5, 7)\), we have \(\mathsf{E}\{T(9,5,7)\} = \frac{1}{p_5 p_7 p_9}\). Thus, to observe the pattern (9, 5, 7), we have to wait on the average until the \(\frac{1}{p_5 p_7 p_9}\)-th repetition. In tossing a fair die, we need to repeat \(\mathsf{E}\{T(3,5)\} = \frac{1}{p_3 p_5} = 36\) times on the average to observe the pattern (3, 5) for the first time. 
4.1.6 (B-2) Overlap** Patterns
We next consider overlap** patterns. When M is an overlap** pattern, construct a non-overlap** pattern
of length \(n+1\) by appropriatelyFootnote 19 choosing x as \(x \notin \left\{ i_1, i_2, \ldots , i_n \right\} \) or \(x \notin \left\{ i_{K_0 +1}, i_{K_1 +1}, \ldots , i_{K_J +1} \right\} \). Then, from (4.A.30), we have
When \(x= i_{n+1}\), using (4.A.32) in (4.A.21), we get
by noting that \(M_x\) in (4.A.31) and \(M_{+1}\) in (4.A.21) are the same. Now, if we consider the case in which M is not an overlap** pattern, the last term of (4.A.33) becomes \(\sum \limits _{j} p_{i_{K_j +1}} \mathsf{E}\left\{ T \left( \tilde{L}_{K_j +1} \right) \right\} = p_{i_{K_0 +1}} \mathsf{E}\left\{ T \left( \tilde{L}_{K_0 +1} \right) \right\} = p_{i_1} \mathsf{E}\left\{ T \left( i_1 \right) \right\} =1\). Consequently, (4.A.33) and (4.A.30) are the same. Thus, for any overlap** or non-overlap** pattern M, we can use (4.A.33) to obtain \(\mathsf{E}\{T(M)\}\).
Example 4.A.6
In the pattern (9, 5, 1, 9, 5), we have \(J=1\), \(K_1=2\), and \(\tilde{L}_{K_1 +1} = (9, 5, 1)\). Thus, from (4.A.30) and (4.A.33), we get \(\mathsf{E}\{T(9,5,1,9,5)\} = \frac{1}{p_{1} p_5^2 p_9^2} - 1 + \left[ p_9 \mathsf{E}\{T(9)\} + p_{1} \mathsf{E}\{T(9,5,1)\} \right] = \frac{1}{p_{1} p_5^2 p_9^2} + \frac{1}{p_5 p_9}\). Similarly, in the pattern (9, 5, 9, 1, 9, 5, 9), we get \(J=2\), \(K_1=1\), \(K_2=3\), and \(\tilde{L}_{K_1 +1} = (9, 5)\) and \(\tilde{L}_{K_2 +1} = (9, 5, 9, 1)\). Therefore,
Comparing Examples 4.A.4 and 4.A.6, it is easy to see that we can obtain \(\mathsf{E}\{T(M)\}\) faster from (4.A.30) and (4.A.33) than from (4.A.21).
Theorem 4.A.1
For a pattern \(M=\left( i_1, i_2, \ldots , i_n \right) \) with J overlap** pieces, the mean time to M can be obtained as
where \(K_1< K_2< \cdots < K_J\) are the lengths of the overlap** pieces with \(K_{J+1} = n\).
Proof
For convenience, let \(\alpha _j = p_{i_{K_j +1}} \mathsf{E}\left\{ T \left( \tilde{L}_{K_j +1} \right) \right\} \) and \(\beta _j = \mathsf{E}\left\{ T\left( L_{K_j} \right) \right\} \). Also let
for \(j=0, 1, \ldots , J-1\), and \(\epsilon _J = 1\) by noting that the term with \(j=J\) is always added in the sum in the right-hand side of (4.A.33). Then, we can rewrite (4.A.33) as
Now, \(\alpha _0 = p_{i_{1}} \mathsf{E}\left\{ T \left( i_1 \right) \right\} = 1\) and \(\alpha _j = \beta _j + 1 - \sum \limits _{l=0}^{j-1} \alpha _l \epsilon _l\) for \(j=1, 2, \ldots , J\) from (4.A.21). Solving for \(\left\{ \alpha _j \right\} _{j=1}^{J}\), we get \(\alpha _1 = \beta _1 +1 - \epsilon _0\), \(\alpha _2 = \beta _2 + 1 - \left( \epsilon _1 \alpha _1 + \epsilon _0 \alpha _0 \right) = \beta _2 - \epsilon _1 \beta _1 + \left( 1 - \epsilon _0\right) \left( 1 - \epsilon _1\right) \), \(\alpha _3 = \beta _3 + 1 - \left( \epsilon _2 \alpha _2 + \epsilon _1 \alpha _1 + \epsilon _0 \alpha _0 \right) = \beta _3 - \epsilon _2 \beta _2 - \epsilon _1\left( 1-\epsilon _2\right) \beta _1 + \left( 1 - \epsilon _0\right) \left( 1 - \epsilon _1\right) \left( 1 - \epsilon _2\right) \), \(\ldots \), and
Therefore,

In the right-hand side of (4.A.39), the second, third, \(\ldots \), second last terms are all 0, and the last term is

Thus, noting (4.A.40) and using (4.A.39) into (4.A.37), we get \(\mathsf{E}\{T(M)\} = \frac{1}{p_{i_1}p_{i_2}\cdots p_{i_n}} - 1 + \beta _J +1\), i.e.,
Next, if we obtain \(\mathsf{E}\left\{ T\left( L_{K_J} \right) \right\} \) after some steps similar to those for (4.A.41) by recollecting that the overlap** pieces of \(L_{K_J}\) are \(L_{K_1}, L_{K_2}, \ldots , L_{K_{J-1}}\), we have \(\mathsf{E}\left\{ T\left( L_{K_J}\right) \right\} = \frac{1}{p_{i_1}p_{i_2}\cdots p_{i_{K_J}}} + \mathsf{E}\left\{ T\left( L_{K_{J-1}} \right) \right\} \). Repeating this procedure, and noting that \(L_1\) is not an overlap** piece, we get (4.A.35) by using (4.A.30). 
Example 4.A.7
Using (4.A.35), it is easy to get \(\mathsf{E}\{T(5,4,4,5)\} = \frac{1+p_4^2 p_5}{p_4^2 p_5^2}\), \(\mathsf{E}\{T(5, 4,5,4)\} = \frac{1+p_4 p_5}{p_4^2 p_5^2}\), \(\mathsf{E}\{T(5, 4, 5, 4, 5)\} = \frac{1}{p_4^2 p_5^3} +\frac{1}{p_4 p_5^2} +\frac{1}{p_5}\), and \(\mathsf{E}\{T(5,4,4,5,4,4, 5)\} = \frac{1}{p_4^4 p_5^3} +\frac{1}{p_4^2 p_5^2} +\frac{1}{p_5}\). 
Example 4.A.8
Assume a coin with \(\mathsf{P}(h) =p =1- \mathsf{P}(t) \), where h and t denote head and tail, respectively. Then, the expected numbers of tosses until the first occurrences of h, tht, htht, ht, hh, and hthhthh are \(\mathsf{E}\{T(h)\} = \frac{1}{p}\), \(\mathsf{E}\{T(tht)\} = \frac{1}{p q^2} +\frac{1}{q}\), \(\mathsf{E}\{T(htht)\} = \frac{1}{p^2 q^2} + \frac{1}{p q}\), \(\mathsf{E}\{T(hthh)\} = \frac{1}{p^3 q} + \frac{1}{p}\), and \(\mathsf{E}\{T(hthhthh)\} = \frac{1}{p^5 q^2} + \frac{1}{p^3 q} +\frac{1}{p}\), respectively, where \(q=1-p\). 
Exercises
Exercise 4.1
Show that
is the pdf of the sum of n i.i.d. exponential random variables with rate \(\mu \).
Exercise 4.2
A box contains three red and two green balls. We choose a ball from the box, discard it, and choose another ball from the box. Let \(X=1\) and \(X=2\) when the first ball is red and green, respectively, and \(Y=4\) and \(Y=3\) when the second ball is red and green, respectively. Obtain the pmf \(p_{X}\) of X, pmf \(p_Y\) of Y, joint pmf \(p_{X,Y}\) of X and Y, conditional pmf \(p_{Y|X}\) of Y given X, conditional pmf \(p_{X|Y}\) of X given Y, and pmf \(p_{X+Y}\) of \(X+Y\).
Exercise 4.3
For two i.i.d. random variables \(X_1\) and \(X_2\) with marginal distribution \(\mathsf{P}(1) = \mathsf{P}(-1)= 0.5\), let \(X_3 = X_1 X_2\). Are \(X_1\), \(X_2\), and \(X_3\) pairwise independent? Are they independent?
Exercise 4.4
When the joint pdf of a random vector (X, Y) is \(f_{X,Y} (x,y) = a \left\{ 1+xy\left( x^2 - y^2 \right) \right\} u ( 1- |x| )u \left( 1- |y|\right) \), determine the constant a. Are X and Y independent of each other? If not, obtain the correlation coefficient between X and Y.
Exercise 4.5
A box contains three red, six green, and five blue balls. A ball is chosen randomly from the box and then replaced to the box after the color is recorded. After six trials, let the numbers of red and blue be R and B, respectively. Obtain the conditional pmf \(p_{R|B=3}\) of R when \(B=3\) and conditional mean \(\mathsf{E}\left\{ R|B=1 \right\} \) of R when \(B=1\).
Exercise 4.6
Two binomial random variables \(X_1 \sim b \left( n_1 , p \right) \) and \(X_2\sim b \left( n_2 , p \right) \) are independent of each other. Show that, when \(X_1 + X_2 =x\) is given, the conditional distribution of \(X_1\) is a hypergeometric distribution.
Exercise 4.7
Show that \(Z=\frac{X}{X+Y} \sim U(0,1)\) for two i.i.d. exponential random variables X and Y.
Exercise 4.8
When the joint pdf of \(\boldsymbol{X}= \left( X_1 , X_2 \right) \) is
obtain the joint pdf \(f_{\boldsymbol{Y}}\) of \(\boldsymbol{Y}= \left( Y_1, Y_2\right) = \left( X_1^2 , X_1 + X_2 \right) \). Based on the joint pdf \(f_{\boldsymbol{Y}}\), obtain the pdf \(f_{Y_1}\) of \(Y_1 = X_1^2\) and pdf \(f_{Y_2}\) of \(Y_2= X_1 + X_2\).
Exercise 4.9
When the joint pdf of \(X_1\) and \(X_2\) is \(f_{X_1 , X_2} (x, y) = \frac{1}{4} u(1-|x|) u(1-|y|)\), obtain the cdf \(F_W\) and pdf \(f_W\) of \(W= \sqrt{ X_1^2 + X_2^2 }\).
Exercise 4.10
Two random variables X and Y are independent of each other with the pdf’s \(f_X (x) = \lambda e^{-\lambda x}u(x)\) and \(f_Y (y) = \mu e^{-\mu y}u(y)\), where \(\lambda >0\) and \(\mu > 0\). When \(W=\min (X,Y)\) and
obtain the joint cdf of (W, V).
Exercise 4.11
Obtain the pdf of \(U=X+Y+Z\) when the joint pdf of X, Y, and Z is \(f_{X,Y,Z}(x,y,z) = \frac{6 u(x) u(y)u(z) }{(1+x+y+z)^{4}} \).
Exercise 4.12
Consider the two joint pdf’s (1) \(f_{\boldsymbol{X}} ( \boldsymbol{x}) = u \left( x_1 \right) u \left( 1- x_1 \right) u \left( x_2 \right) u \left( 1-x_2 \right) \) and (2) \(f_{\boldsymbol{X}} (\boldsymbol{x}) = 2 u \left( x_1 \right) u \left( 1- x_2 \right) u \left( x_2 -x_1 \right) \) of \(\boldsymbol{X}= \left( X_1 , X_2 \right) \), where \(\boldsymbol{x}= \left( x_1, x_2 \right) \). In each of the two cases, obtain the joint pdf \(f_{\boldsymbol{Y}}\) of \(\boldsymbol{Y}= \left( Y_1, Y_2\right) = \left( X_1^2 , X_1 + X_2 \right) \), and then, obtain the pdf \(f_{Y_1}\) of \(Y_1 = X_1^2\) and pdf \(f_{Y_2}\) of \(Y_2= X_1 + X_2\) based on \(f_{\boldsymbol{Y}}\).
Exercise 4.13
In each of the two cases of the joint pdf \(f_{\boldsymbol{X}}\) described in Exercise 4.12, obtain the joint pdf \(f_{\boldsymbol{Y}}\) of \(\boldsymbol{Y}= \left( Y_1, Y_2\right) = \left( \frac{1}{2} \left( X_1^2 + X_2 \right) , \frac{1}{2} \left( X_1^2 - X_2 \right) \right) \), and then, obtain the pdf \(f_{Y_1}\) of \(Y_1\) and pdf \(f_{Y_2}\) of \(Y_2\) based on \(f_{\boldsymbol{Y}}\).
Exercise 4.14
Two random variables \(X \sim G\left( \alpha _1 , \beta \right) \) and \(Y \sim G\left( \alpha _2 , \beta \right) \) are independent of each other. Show that \(Z=X+Y\) and \(W=\frac{X}{Y}\) are independent of each other and obtain the pdf of Z and pdf of W.
Exercise 4.15
Denote the joint pdf of \(\boldsymbol{X}= \left( X_1 , X_2 \right) \) by \(f_{\boldsymbol{X}}\).
-
(1)
Express the pdf of \(Y_1 = \left( X_1^2 +X_2^2 \right)^r\) in terms of \(f_{\boldsymbol{X}}\).
-
(2)
When \(f_{\boldsymbol{X}} (x, y) = \frac{1}{\pi } u \left( 1- x^2 - y^2 \right) \), show that the cdf \(F_W\) and pdf \(f_W\) of \(W= \left( X_1^2 + X_2^2 \right)^r\) are as follows:
-
1.
\(F_W (w)= u(w-1)\) and \(f_W (w) = \delta ( w-1)\) if \(r = 0\).
-
2.
\(F_W ( w ) = \left\{ \begin{array}{ll} 0, &{} w \le 0, \\ w^{\frac{1}{r}}, &{} 0 \le w \le 1, \\ 1, &{} w \ge 1 \end{array} \right. \) and \(f_W ( w ) = \frac{1}{r} w^{\frac{1}{r}-1} u(w) u(1-w)\) if \(r > 0\).
-
3.
\(F_W (w) = \left\{ \begin{array}{ll} 0, &{} w < 1, \\ 1- w^{\frac{1}{r}}, &{} w \ge 1 \end{array} \right. \) and \(f_W (w) =-\frac{1}{r} w^{\frac{1}{r} -1} u(w - 1)\) if \(r < 0\).
-
1.
-
(3)
Obtain \(F_W\) and \(f_W\) when \(r= \frac{1}{2} \), 1, and \(-1\) in (2).
Exercise 4.16
The marginal pdf of the three i.i.d. random variables \(X_1\), \(X_2\), and \(X_3\) is \(f(x) = u(x) u(1-x)\).
-
(1)
Obtain the joint pdf \(f_{Y_1 , Y_2}\) of \(\left( Y_1 , Y_2 \right) = \left( X_1 + X_2 + X_3 , X_1 - X_3 \right) \).
-
(2)
Based on \(f_{Y_1 , Y_2}\), obtain the pdf \(f_{Y_2}\) of \(Y_2\).
-
(3)
Based on \(f_{Y_1 , Y_2}\), obtain the pdf \(f_{Y_1}\) of \(Y_1\).
Exercise 4.17
Consider i.i.d. random variables X and Y with marginal pmf \(p (x) = (1-\alpha )\alpha^{x-1} \tilde{u} (x-1)\), where \(0< \alpha <1\).
-
(1)
Obtain the pmf of \(X+Y\) and pmf of \(X-Y\).
-
(2)
Obtain the joint pmf of \((X-Y, X)\) and joint pmf of \((X-Y, Y)\).
-
(3)
Using the results in (2), obtain the pmf of X, pmf of Y, and pmf of \(X-Y\).
-
(4)
Obtain the joint pmf of \((X+Y, X-Y)\), and using the result, obtain the pmf of \(X-Y\) and pmf of \(X+Y\). Compare the results with those obtained in (1).
Exercise 4.18
Consider Exercise 2.30. Let \(R_n\) be the number of type O cells at \(n+ \frac{1}{2} \) minutes after the start of the culture. Obtain \(\mathsf{E}\left\{ R_n \right\} \), the pmf \(p_2(k)\) of \(R_2\), and the probability \(\eta _0\) that nothing will remain in the culture.
Exercise 4.19
Obtain the conditional expected value \(\mathsf{E}\{ X | Y=y\}\) in Example 4.4.3.
Exercise 4.20
Consider an i.i.d. random vector \(\boldsymbol{X}=\left( X_1 , X_2 , X_3 \right) \) with marginal pdf \(f(x) = e^{-x} u(x)\). Obtain the joint pdf \(f_{\boldsymbol{Y}}\left( y_1,y_2,y_3 \right) \) of \(\boldsymbol{Y}= \left( Y_1, Y_2, Y_3 \right) \), where \(Y_1=X_1+X_2+X_3\), \(Y_2=\frac{X_1+X_2}{X_1+X_2+X_3}\), and \(Y_3=\frac{X_1}{X_1+X_2}\).
Exercise 4.21
Consider two i.i.d. random variables \(X_1\) and \(X_2\) with marginal pdf \(f(x) = u(x)u(1-x)\). Obtain the joint pdf of \(\boldsymbol{Y}= \left( Y_1, Y_2 \right) \), pdf of \(Y_1\), and pdf of \(Y_2\) when \(Y_1=X_1+X_2\) and \(Y_2=X_1 - X_2\).
Exercise 4.22
When \(\boldsymbol{Y}=\left( Y_1, Y_2 \right) \) is obtained from rotating clockwise a point \(\boldsymbol{X}= \left( X_1 , X_2 \right) \) in the two dimensional plane by \(\theta \), express the pdf of \(\boldsymbol{Y}\) in terms of the pdf \(f_{\boldsymbol{X}}\) of \(\boldsymbol{X}\).
Exercise 4.23
Assume that the value of the joint pdf \(f_{X,Y} (x, y)\) of X and Y is positive in a region containing \(x^2+y^2<a^2\), where \(a > 0\). Express the conditional joint cdf \(F_{X,Y|A}\) and conditional joint pdf \(f_{X,Y|A}\) in terms of \(f_{X,Y}\) when \(A= \left\{ X^2+Y^2 \le a^2 \right\} \).
Exercise 4.24
The joint pdf of (X, Y) is \(f_{X,Y} (x, y) = \frac{1}{4} u \left( 1- |x|\right) u \left( 1- |y|\right) \). When \(A= \left\{ X^2+Y^2 \le a^2 \right\} \) with \(0< a< 1\), obtain the conditional joint cdf \(F_{X,Y|A}\) and conditional joint pdf \(f_{X,Y|A}\).
Exercise 4.25
Prove the following results:
-
(1)
If X and Z are not orthogonal, then there exists a constant a for which Z and \(X-aZ\) are orthogonal.
-
(2)
It is possible that X and Y are uncorrelated even when X and Z are correlated and Y and Z are correlated.
Exercise 4.26
Prove the following results:
-
(1)
If X and Y are independent of each other, then they are uncorrelated.
-
(2)
If the pdf \(f_X\) of X is an even function, then X and \(X^2\) are uncorrelated but are not independent of each other.
Exercise 4.27
Show that
where \(\rho \) is the correlation coefficient between the random variables X and Y both with zero mean and unit variance.
Exercise 4.28
Consider a random vector \(\boldsymbol{X}= \left( X_1 , X_2 , X_3 \right)^T\) with covariance matrix \(\boldsymbol{K}_{\boldsymbol{X}} = \left( \begin{array}{ccc} 2 &{} 1 &{} 1 \\ 1 &{} 2 &{} 1 \\ 1 &{} 1 &{} 2 \end{array} \right) \). Obtain a linear transformation making \(\boldsymbol{X}\) into an uncorrelated random vector with unit variance.
Exercise 4.29
Obtain the pdf of Y when the joint pdf of (X, Y) is \(f_{X,Y}(x, y) = \frac{1}{y} \exp \left( -y - \frac{x}{y} \right) u(x)u(y)\).
Exercise 4.30
When the joint pmf of (X, Y) is
obtain the pmf of X and pmf of Y.
Exercise 4.31
For two i.i.d random variables \(X_1\) and \(X_2\) with marginal pmf \(p(x) = e^{-\lambda }\frac{\lambda^x}{x!} \tilde{u} (x)\), where \(\lambda >0\), obtain the pmf of \(M=\max \left( X_1 , X_2 \right) \) and pmf of \(N=\min \left( X_1 , X_2 \right) \).
Exercise 4.32
For two i.i.d. random variables X and Y with marginal pdf \(f(z) = u(z) - u(z-1)\), obtain the pdf’s of \(W=2X\), \(U=-Y\), and \(Z=W+U\).
Exercise 4.33
For three i.i.d. random variables \(X_1\), \(X_2\), and \(X_3\) with marginal distribution \(U\left[ - \frac{1}{2} , \frac{1}{2} \right] \), obtain the pdf of \(Y=X_1+X_2+X_3\) and \(\mathsf{E}\left\{ Y^4 \right\} \).
Exercise 4.34
The random variables \(\left\{ X_i \right\} _{i=1}^{n}\) are independent of each other with pdf’s \(\left\{ f_i \right\} _{i=1}^{n}\), respectively. Obtain the joint pdf of \(\left\{ Y_k \right\} _{k=1}^{n}\), where \( Y_k = X_1 + X_2 + \cdots + X_k\) for \(k=1, 2 , \ldots , n\).
Exercise 4.35
The joint pmf of X and Y is
-
(1)
Obtain the pmf of X and pmf of Y.
-
(2)
Obtain \( \mathsf{P}(X>Y)\), \( \mathsf{P}(Y=2X)\), \( \mathsf{P}(X+Y=3)\), and \( \mathsf{P}(X \le 3-Y)\).
-
(3)
Discuss whether or not X and Y are independent of each other.
Exercise 4.36
For independent random variables \(X_1\) and \(X_2\) with pdf’s \(f_{X_1}(x) = u(x)u(1-x)\) and \(f_{X_2}(x)= e^{-x}u(x)\), obtain the pdf of \(Y=X_1+X_2\).
Exercise 4.37
Three Poisson random variables \(X_1\), \(X_2\), and \(X_3\) with means 2, 1, and 4, respectively, are independent of each other.
-
(1)
Obtain the mgf of \(Y=X_1+X_2+X_3\).
-
(2)
Obtain the distribution of Y.
Exercise 4.38
When the joint pdf of X, Y, and Z is \(f_{X,Y,Z} (x, y, z) = k (x+y+z) u(x)u(y) u(z)u(1-x)u(1-y)u(1-z)\), determine the constant k and obtain the conditional pdf \(f_{Z|X,Y} ( z | x , y)\).
Exercise 4.39
Consider a random variable with probability measure
Here, \(\lambda \) is a realization of a random variable \(\Lambda \) with pdf \(f_{\Lambda }(v) = e^{-v}u(v)\). Obtain \(\mathsf{E}\left. \left\{ e^{-\Lambda } \right| X=1 \right\} \).
Exercise 4.40
When \(U_1\), \(U_2\), and \(U_3\) are independent of each other, obtain the joint pdf \(f_{X, Y, Z} ( x, y,z)\) of \(X = U_1\), \(Y = U_1 + U_2\), and \(Z= U_1 + U_2 + U_3\) in terms of the pdf’s of \(U_1\), \(U_2\), and \(U_3\).
Exercise 4.41
Let (X, Y, Z) be the rectangular coordinate of a randomly chosen point in a sphere of radius 1 centered at the origin in the three dimensional space.
-
(1)
Obtain the joint pdf \(f_{X,Y} (x,y)\) and marginal pdf \(f_X (x)\).
-
(2)
Obtain the conditional joint pdf \(f_{X,Y|Z}( x,y | z)\). Are X, Y, and Z independent of each other?
Exercise 4.42
Consider a random vector (X, Y) with joint pdf \( f_{X, Y} (x,y) = c \, u \left( r- |x| - |y| \right) \), where c is a constant and \(r>0\).
-
(1)
Express c in terms of r and obtain the pdf \(f_X (x)\).
-
(2)
Are X and Y independent of each other?
-
(3)
Obtain the pdf of \(Z = |X|+|Y|\).
Exercise 4.43
Assume X with cdf \(F_X\) and Y with cdf \(F_Y\) are independent of each other. Show that \( \mathsf{P}(X \ge Y ) \ge \frac{1}{2} \) when \(F_X(x) \le F_Y(x)\) at every point x.
Exercise 4.44
The joint pdf of (X, Y) is \( f_{X, Y} (x,y) = c\left( x^2 + y^2 \right) u(x)u(y) u \left( 1 - x^2 - y^2\right) \).
-
(1)
Determine the constant c and obtain the pdf of X and pdf of Y. Are X and Y independent of each other?
-
(2)
Obtain the joint pdf \(f_{R, \varTheta }\) of \(R= \sqrt{X^2 + Y^2}\) and \(\varTheta = \tan^{-1} \frac{Y}{X}\).
-
(3)
Obtain the pmf of the output \(Q = q (R, \varTheta )\) of polar quantizer, where
$$\begin{aligned} q ( r, \theta ) = \left\{ \begin{array}{ll} k, &{} \text{ if } 0 \le r \le \left( \frac{1}{2} \right)^{\frac{1}{4}}, \; \frac{\pi (k-1)}{8} \le \theta \le \frac{\pi k}{8},\\ k+4, &{} \text{ if } \left( \frac{1}{2} \right)^{\frac{1}{4}} \le r \le 1, \; \frac{\pi (k-1)}{8} \le \theta \le \frac{\pi k}{8} \end{array} \right. \end{aligned}$$(4.E.8)for \(k=1, 2, 3, 4\).
Exercise 4.45
Two types of batteries have the pdf \(f(x) = 3\lambda x^2 \exp (-\lambda x^3)u(x)\) and \(g(y) =3\mu y^2 \exp (-\mu y^3)u(y)\), respectively, of lifetime with \(\mu >0\) and \(\lambda >0\). When the lifetimes of batteries are independent of each other, obtain the probability that the battery with pdf f of lifetime lasts longer than that with g, and obtain the value when \(\lambda =\mu \).
Exercise 4.46
Two i.i.d. random variables X and Y have marginal pdf \(f(x) = e^{-x} u(x)\).
-
(1)
Obtain the pdf each of \(U=X+Y\), \(V=X-Y\), XY, \(\frac{X}{Y}\), \(Z=\frac{X}{X+Y}\), \(\min (X,Y)\), \(\max (X,Y)\), and \(\frac{\min (X,Y)}{\max (X,Y)}\).
-
(2)
Obtain the conditional pdf of V when \(U=u\).
-
(3)
Show that U and Z are independent of each other.
Exercise 4.47
Two Poisson random variables \(X_1 \sim P \left( \lambda _1 \right) \) and \(X_2 \sim P \left( \lambda _2 \right) \) are independent of each other.
-
(1)
Show that \(X_1+X_2 \sim P \left( \lambda _1 + \lambda _2 \right) \).
-
(2)
Show that the conditional distribution of \(X_1\) when \(X_1+X_2=n\) is \(b \left( n, \frac{\lambda _1 }{\lambda _1 + \lambda _2 }\right) \).
Exercise 4.48
Consider Exercise 2.17.
-
(1)
Obtain the mean and variance of the number M of matches.
-
(2)
Assume that the students with matches will leave with their balls, and each of the remaining students will pick a ball again after their balls are mixed. Show that the mean of the number of repetitions until every student has a match is N.
Exercise 4.49
A particle moves back and forth between positions \(0, 1, \ldots , n\). At any position, it moves to the previous or next position with probability \(1-p\) or p, respectively, after 1 second. At positions 0 and n, however, it moves only to the next position 1 and previous position \(n-1\), respectively. Obtain the expected value of the time for the particle to move from position 0 to position n.
Exercise 4.50
Let N be the number of tosses of a coin with probability p of head until we have two head’s in the last three tosses: we let \(N=2\) if the first two outcomes are both head’s. Obtain the expected value of N.
Exercise 4.51
Two people \(A_1\) and \(A_2\) with probabilities \(p_{1}\) and \(p_{2}\), respectively, of hit alternatingly fire at a target until the target has been hit two times consecutively.
-
(1)
Obtain the mean number \(\mu _i\) of total shots fired at the target when \(A_i\) starts the shooting for \(i=1, 2\).
-
(2)
Obtain the mean number \(h_i\) of times the target has been hit when \(A_i\) starts the shooting for \(i=1, 2\).
Exercise 4.52
Consider Exercise 4.51, but now assume that the game ends when the target is hit twice (i.e., consecutiveness is unnecessary). When \(A_1\) starts, obtain the probability \(\alpha _1\) that \(A_1\) fires the last shot of the game and the probability \(\alpha _2\) that \(A_1\) makes both hits.
Exercise 4.53
Assume i.i.d. random variables \(X_1 , X_2 , \ldots \) with marginal distribution U[0, 1). Let \(g(x)=\mathsf{E}\{N\}\), where \(N=\min \left\{ n: \, X_n <X_{n-1} \right\} \) and \(X_0=x\). Obtain an integral equation for g(x) conditional on \(X_1\), and solve the equation.
Exercise 4.54
We repeat tossing a coin with probability p of head. Let X be the number of repetitions until head appears three times consecutively.
-
(1)
Obtain a difference equation for \(g(k)= \mathsf{P}(X=k)\).
-
(2)
Obtain the generating function \(G_X(s) = \mathsf{E}\left\{ s^X \right\} \).
-
(3)
Obtain \(\mathsf{E}\{X\}\). (Hint. Use conditional expected value.)
Exercise 4.55
Obtain the conditional joint cdf \(F_{X,Y|A} (x,y)\) and conditional joint pdf \(f_{X,Y|A}(x,y)\) when \(A=\left\{ x_1 < X \le x_2 \right\} \).
Exercise 4.56
For independent random variables X and Y, assume the pmf
of X and pmf
of Y. Obtain the conditional pmf’s \(p_{X|Z}\), \(p_{Z|X}\), \(p_{Y|Z}\), and \(p_{Z|Y}\) and the joint pmf’s \(p_{X,Y}\), \(p_{Y,Z}\), and \(p_{X,Z}\) when \(Z=X-Y\).
Exercise 4.57
Two exponential random variables \(T_1\) and \(T_2\) with rate \(\lambda _1\) and \(\lambda _2\), respectively, are independent of each other. Let \(U=\min \left( T_1, T_2 \right) \), \(V=\max \left( T_1, T_2 \right) \), and I be the smaller index, i.e., the index I such that \(T_I =U\).
-
(1)
Obtain the expected values \(\mathsf{E}\{U\}\), \(\mathsf{E}\{V-U\}\), and \(\mathsf{E}\{V\}\).
-
(2)
Obtain \(\mathsf{E}\{V\}\) using \(V=T_1+T_2-U\).
-
(3)
Obtain the joint pdf \(f_{U, V-U, I}\) of \((U, V-U, I)\).
-
(4)
Are U and \(V-U\) independent of each other?
Exercise 4.58
Consider a bi-variate beta random vector (X, Y) with joint pdf
where \(p_{1}\), \(p_2\), and \(p_3\) are positive numbers. Obtain the pdf \(f_{X}\) of X, pdf \(f_{Y}\) of Y, conditional pdf \(f_{X|Y}\), and conditional pdf \(f_{Y|X}\). In addition, obtain the conditional pdf \(f_{\left. \frac{Y}{1-X} \right| X}\) of \(\frac{Y}{1-X}\) when X is given.
Exercise 4.59
Assuming the joint pdf \(f_{X,Y} (x, y) = \frac{1}{16} u\left( 2-|x| \right) u\left( 2-|y| \right) \) of (X, Y), obtain the conditional joint cdf \(F_{X,Y|B}\) and conditional joint pdf \(f_{X,Y|B}\) when \(B = \left\{ |X| + |Y| \le 1 \right\} \).
Exercise 4.60
Let the joint pdf of X and Y be \(f_{X,Y} (x, y) = |xy| u(1-|x|)u (1-|y| )\). When \(A= \left\{ X^2+Y^2 \le a^2 \right\} \) with \(0< a< 1\), obtain the conditional joint cdf \(F_{X,Y|A}\) and conditional joint pdf \(f_{X,Y|A}\).
Exercise 4.61
For a random vector \(\boldsymbol{X}= \left( X_1 , X_2 , \ldots , X_n \right) \), show that
where \(\boldsymbol{R}\) is the correlation matrix of \(\boldsymbol{X}\) and \(\boldsymbol{R}^{-1}\) is the inverse matrix of \(\boldsymbol{R}\).
Exercise 4.62
When the cf of (X, Y) is \(\varphi _{X,Y}(t, s)\), show that the cf of \(Z=aX+bY\) is \(\varphi _{X,Y}(at,bt)\).
Exercise 4.63
The joint pdf of (X, Y) is
where i, k, and n are natural numbers such that \(1 \le i < k \le n\), F is the cdf of a random variable, and \(f(t) = \frac{d}{dt} F(t)\). Obtain the pdf of X and pdf of Y.
Exercise 4.64
The number N of typographical errors in a book is a Poisson random variable with mean \(\lambda \). Proofreaders A and B find a typographical error with probability \(p_{1}\) and \(p_2\), respectively. Let \(X_1\), \(X_2\), \(X_3\), and \(X_4\) be the numbers of typographical errors found by Proofreader A but not by Proofreader B, by Proofreader B but not by Proofreader A, by both proofreaders, and by neither proofreader, respectively. Assume that the event of a typographical error being found by a proofreader is independent of that by another proofreader.
-
(1)
Obtain the joint pmf of \(X_1\), \(X_2\), \(X_3\), and \(X_4\).
-
(2)
Show that
$$\begin{aligned} \frac{\mathsf{E}\left\{ X_1 \right\} }{\mathsf{E}\left\{ X_3 \right\} } = \frac{1-p_2}{p_2}, \quad \frac{\mathsf{E}\left\{ X_2 \right\} }{\mathsf{E}\left\{ X_3 \right\} } = \frac{1-p_{1}}{p_{1}}. \end{aligned}$$(4.E.14)Now assume that the values of \(p_{1}\), \(p_2\), and \(\lambda \) are not available.
-
(3)
Using \(X_i\) as the estimate of \(\mathsf{E}\left\{ X_i \right\} \) for \(i= 1, 2, 3\), obtain the estimates of \(p_{1}\), \(p_2\), and \(\lambda \).
-
(4)
Obtain an estimate of \(X_4\).
Exercise 4.65
Show that the correlation coefficient between X and |X| is
where \(m_X^{\pm }\), f, \(m_X\), and \(\sigma _X^2\) are the half means defined in (3.E.28), pdf, mean, and variance, respectively, of X. Obtain the value of \(\rho _{X |X|}\) and compare it with what can be obtained intuitively in each of the following cases of the pdf \(f_X(x)\) of X:
-
(1)
\(f_X(x)\) is an even function.
-
(2)
\(f_X(x) >0\) only for \(x \ge 0\).
-
(3)
\(f_X(x) >0\) only for \(x \le 0\).
Exercise 4.66
For a random variable X with pdf \(f_X (x) = u(x) - u(x-1)\), obtain the joint pdf of X and \(Y=2X+1\).
Exercise 4.67
Consider a random variable X and its magnitude \(Y=|X|\). Show that the conditional pdf \(f_{X | Y}\) can be expressed as
for \(y \in \left\{ y\,| \, \left\{ f_X(y) + f_X(-y) \right\} u(y) > 0 \right\} \), where \(f_X\) is the pdf of X. Obtain the conditional pdf \(f_{Y|X}(y|x)\). (Hint. Use (4.5.15).)
Exercise 4.68
Show that the joint cdf and joint pdf are
and
respectively, for X and \(Y=cX+a\).
Exercise 4.69
Let f and F be the pdf and cdf, respectively, of a continuous random variable X, and let \(Y=X^2\).
-
(1)
Obtain the joint cdf \(F_{X,Y}\).
-
(2)
Obtain the joint pdf \(f_{X,Y}\), and then confirm \( \int _{-\infty }^{\infty } f_{X,Y} (x,y) dy = f(x)\) and
$$\begin{aligned} \int _{-\infty }^{\infty } f_{X,Y} (x,y) dx = \frac{1}{2 \sqrt{y}} \left\{ f \left( \sqrt{y} \right) + f \left( -\sqrt{y} \right) \right\} u(y) \end{aligned}$$(4.E.19)by integration.
-
(3)
Obtain the conditional pdf \(f_{X|Y}\).
Exercise 4.70
Show that the pdf \(f_{X, cX}\) shown in (4.5.9) satisfies \( \int _{-\infty }^{\infty } \int _{-\infty }^{\infty } f_{X, cX} (x,y) dy dx = 1\).
Exercise 4.71
Express the joint cdf and joint pdf of the input X and output \(Y=Xu(X)\) of a half-wave rectifier in terms of the pdf \(f_X\) and cdf \(F_X\) of X.
Exercise 4.72
Obtain (4.5.2) from \(F_{X, X+a} (x,y) = F_X \left( \min (x,y-a) \right) \) shown in (4.5.1).
Exercise 4.73
Assume that the joint pdf of \(\boldsymbol{X}= \left( X_1 , X_2 \right) \) is
Determine c. Obtain and sketch the pdfs of \(X_1\) and \(X_2\).
Exercise 4.74
Consider a random vector \(\boldsymbol{X}= \left( X_1, X_2\right) \) with the pdf \(f_{\boldsymbol{X}} \left( x_1, x_2 \right) = u \left( x_1 \right) u \left( 1 - x_1 \right) u \left( x_2 \right) u \left( 1-x_2 \right) \).
-
(1)
Obtain the joint pdf \(f_{\boldsymbol{Y}}\) of \(\boldsymbol{Y}= \left( Y_1, Y_2\right) = \left( X_1 - X_2 , X_1^2 - X_2^2 \right) \).
-
(2)
Obtain the pdf \(f_{Y_1}\) of \(Y_1\) and pdf \(f_{Y_2}\) of \(Y_2\) from \(f_{\boldsymbol{Y}}\).
-
(3)
Compare the pdf \(f_{Y_2}\) of \(Y_2\) with that we can obtain from
$$\begin{aligned} f_{aX^2}(y) = \frac{1}{2\sqrt{ay}} \left\{ f_X\left( \sqrt{\frac{y}{a}} \right) +f_X \left( -\sqrt{\frac{y}{a}}\right) \right\} u(y) \end{aligned}$$(4.E.21)for \(a > 0\) shown in (3.2.35) and
$$\begin{aligned} f_{X_1 - X_2 } ( y ) = \int _{-\infty }^{\infty } f_{X_1 , X_2}\left( y + y_2,y_2\right) dy_2 \end{aligned}$$(4.E.22)shown in (4.2.20).
Rights and permissions
Copyright information
© 2022 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this chapter
Cite this chapter
Song, I., Park, S.R., Yoon, S. (2022). Random Vectors. In: Probability and Random Variables: Theory and Applications. Springer, Cham. https://doi.org/10.1007/978-3-030-97679-8_4
Download citation
DOI: https://doi.org/10.1007/978-3-030-97679-8_4
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-97678-1
Online ISBN: 978-3-030-97679-8
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


 will become
will become  .
. , for example, can more specifically be written as
, for example, can more specifically be written as  .
. and
and  can of course be obtained with the pmf’s of
can of course be obtained with the pmf’s of  and
and 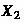 obtained already in Example
obtained already in Example  of
of  should be differentiated from the pdf
should be differentiated from the pdf  of the product XY. In other cases, we do not need to use commas: for instance,
of the product XY. In other cases, we do not need to use commas: for instance,  ,
,  ,
,  denote relations among two or more random variables and thus is expressed without any comma.
denote relations among two or more random variables and thus is expressed without any comma. such that
such that  is called Hermitian.
is called Hermitian. such that
such that  is normal.
is normal. is unitary if
is unitary if  or if
or if  . In the real space, a unitary matrix is referred to as an orthogonal matrix. A Hermitian matrix is always a normal matrix and a unitary matrix is always a normal matrix, but the converses are not necessarily true: for example,
. In the real space, a unitary matrix is referred to as an orthogonal matrix. A Hermitian matrix is always a normal matrix and a unitary matrix is always a normal matrix, but the converses are not necessarily true: for example,  is normal, but is neither Hermitian nor unitary.
is normal, but is neither Hermitian nor unitary. .
.