Abstract
Is truth – qua a primitive notion – fit to play an independent role in the philosophy of mathematics and in the foundational investigations? The problem is handled by surveying axiomatic theories of truth and their implications, with a main concern for ontological and epistemological issues.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
Research partially supported by PRIN 2017.
- 2.
Cantini (2017) being dedicated mainly to Feferman’s work.
- 3.
See Feferman (1998a) pp.123–24.
- 4.
The model we have in mind derives from practice, it is simply either the set of informal elucidations that precede the informal presentation or development of a theory, axiomatic or not.
- 5.
Let me cite Tarski himself, Tarski (1944), p.352: When a language is unable to define truth, we then have to include the term “true” or some other semantic term, in the list of undefined terms of the meta-language, and to express fundamental properties of the notion of truth in a series of axioms. There is nothing essentially wrong in such an axiomatic procedure, and it may prove useful for various purposes.
In Tarski (1956), p.266, Tarski similarly writes that for some of the languages for which truth cannot be defined, we can nevertheless make “consistent and correct use” of the concept of truth by way of taking truth as a primitive notion, and giving it content by introducing the relevant sorts of axioms.
- 6.
- 7.
- 8.
- 9.
See Weyl (1910).
- 10.
- 11.
E.g. permutations, duplications, identification, expansion of variables.
- 12.
For all these theories, we refer to the monograph (Halbach, 2011).
- 13.
Formulas generated from atomic formulas via Boolean operations and bounded quantifiers
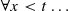 and ∃x < t… with < representing the standard ordering on natural numbers.
and ∃x < t… with < representing the standard ordering on natural numbers. - 14.
See Theorem 3.2 in Fischer (2014).
- 15.
- 16.
These are neatly analyzed probably for the first time by Weyl (1910).
- 17.
Note that this excludes the principles about very large cardinals, determinacy, etc.
- 18.
Typically this happens for the Liar sentence L.
References
Aczel, P. 1980. Frege structures and the notions of proposition, truth and set. In The Kleene Symposium, ed. J. Barwise, H. Keisler, and K. Kunen, 31–59. Amsterdam: North Holland.
Aczel, P., and M. Rathjen. 2001. Notes on constructive set theory. Technical Report 40, Institut Mittag-Leffler, Djursholm.
Burgess, J. 2014. Friedman and the axiomatization of Kripke’s theory of truth. In Foundational adventures: Essays in honor of Harvey M. Friedman, ed. N. Tennant, 125–128. London: College Publications.
Caldon, P., and A. Ignjatovic. 2005. On mathematical instrumentalism. Journal of Symbolic Logic 50: 778–794.
Cantini, A. 1985a. A note on a predicatively reducible theory of iterated elementary induction. Bollettino dell’Unione Matematica Italiana 6(2): 1–17.
Cantini, A. 1985b. Una nota sulla concezione semi–intuizionistica della matematica. Rivista di Filosofia 69: 465–486.
Cantini, A. 1989. Notes on formal theories of truth. Zeitschrift f. Math. Logik u. Grundlagen der Mathematik 35: 97–130.
Cantini, A. 1990. A theory of formal truth arithmetically equivalent to I D1. Journal of Symbolic Logic 55: 244–259.
Cantini, A. 1996. Logical Frameworks for Truth and Abstraction. Amsterdam: North Holland.
Cantini, A. 2016. About truth and types. In Advances in proof theory, volume 28 of Progress in computer science and applied logic, ed. R. Kahle, T. Strahm, and T. Studer, 287–314. Cham: Birkhäuser–Springer.
Cantini, A. 2017. Feferman and the truth. In Feferman on foundations, volume 17 of Outstanding contributions to logic, ed. G. Jäger and W. Sieg, 31–64. Cham: Springer.
Cantini, A. 2020. A fixed point theory over stratified truth. Mathematical Logic Quarterly. to appear, 17 pages.
Cantini, A., and L. Crosilla. 2010. Elementary constructive operational set theory. In Ways of proof theory, ed. R. Schindler, 199–240. Frankfurt: Ontos Verlag.
Cellucci, C. 2017. Rethinking knowledge: The heuristic view. Cham: Springer.
Cieśliński, C., M. Łełyk, and B. Wcisło. 2017. Models of PT− with internal induction for total formulae. Review of Symbolic Logic 10: 187–202.
Crosilla, L. 2017. Predicativity and Feferman. In Feferman on foundations, volume 17 of Outstanding contributions to logic, ed. G. Jäger, and W. Sieg, 423–447. Cham: Springer.
Dummett, M. 2004. Truth and the past. New York: Columbia U.P.
Ehrenfeucht, A., and J. Mycielski. 2020. Abbreviating proofs by adding new axioms. Bulletin of the American Mathematical Society 77: 366–367.
Enayat, A., M. Lełyk, and B. Wcisło. 2020. Truth and feasible reducibility. Journal of Symbolic Logic 85: 367–421.
Enayat, A., and A. Visser. 2015. New constructions of satisfaction classes. In Unifying the philosophy of truth, Number 36 in Log. Epistemol. Unity Sci., ed. T. Achourioti, H. Galinon, J.M. Martinez, and K. Fujimoto, 321–35. Cham: Springer.
Feferman, S. 1979. Constructive theories of functions and classes. In Logic colloquium ’78, ed. M. Boffa and D. van Dalen, 159–224. Amsterdam: North Holland.
Feferman, S. 1982. Iterated inductive fixed-point theories: Application to Hancock’s conjecture. In Patras Logic Symposion ’80, ed. G.E.A. Metakides, 171–196. Amsterdam: North Holland.
Feferman, S. 1998a. In the light of logic. Oxford: Oxford University Press.
Feferman, S. 1998b. Weyl vindicated: Das Kontinuum 70 years later. In In the light of logic, 249–283. Oxford: Oxford University Press.
Feferman, S. 1998c. Working foundations ’91. See Feferman (1998a ), 105–124.
Feferman, S. 2008. Axioms for determinateness and truth. Review of Symbolic Logic 1: 204–217.
Fischer, M. 2014. Truth and speed-up. Review of Symbolic Logic 7: 319–340.
Fischer, M., L. Horsten, and C. Nicolai. 2017. Iterated reflection over full disquotational truth. Journal of Logic and Computation 27: 2613–2651.
Fischer, M., L. Horsten, and C. Nicolai. 2019. Hypatia’s silence. Nous 20: 1–24.
Fujimoto, K. 2011. Autonomous progressions and transfinite iteration of self-applicable truth. Journal of Symbolic Logic 76: 914–945.
Fujimoto, K. 2018. Truths, inductive definitions, and Kripke–Platek systems over set theory. Journal of Symbolic Logic 83: 868–898.
Fujimoto, K. 2019. Predicativism about classes. Journal of Philosophy 116: 206–229.
Girard, J. 1987. Proof theory and logical complexity. Naples: Bibliopolis.
Glass, T. 1996. On power set in explicit mathematics. Journal of Symbolic Logic 61(2): 468–489.
Gödel, K. 1986. Über die länge von beweisen. In Collected works, Vol. I, ed. S. Feferman and et al., 123–153. Oxford: Oxford University Press.
Halbach, V. 2011. Axiomatic theories of truth, 1st ed. Cambridge: Cambridge University Press.
Halbach, V., and H. Horsten. 2006. Axiomatizing Kripke’s theory of truth. Journal of Symbolic Logic 71(2): 677–712.
Hilbert, D. 2013. David Hilbert’s lectures on the foundations of arithmetic and logic, 1917–1933. Cham: Springer.
Horsten, L. 2011. The Tarskian turn. Deflationism and axiomatic truth. Cambridge: MIT Press.
Horsten, L., and G. Leigh. 2017. Truth is simple. Mind 126: 195–232.
Jäger, G. 1997. Power types in explicit mathematics? Journal of Symbolic Logic 62: 1142–1146.
Jäger, G. 2005. Metapredicative and explicit Mahlo: A proof-theoretic perspective. In Logic colloquium 2000, Lecture notes in logic 19, ed. R. Cori, A. Razborov, S. Todorcevic, and C. Wood, 272–293. Urbana: Association for Symbolic Logic.
Jäger, G., R. Kahle, A. Setzer, and T. Strahm. 1999. The proof-theoretic analysis of transfinitely iterated fixed point theories. Journal of Symbolic Logic 64: 53–67.
Kaye, R. 2005. Models of peano arithmetic. Lecture notes in logic 19. Urbana: Association for Symbolic Logic.
Kotlarski, H., and A. Lachlan. 1981. Construction of satisfaction classes for nonstandard models. Canadian Mathematical Bulletin 24: 283–93.
Kreisel, G. 1970. Principles of proof and ordinals implicit in given concepts. In Intuitionism and Proof Theory, ed. A. Kino, J. Myhill, and R.E. Vesley, 489–516. Amsterdam: North Holland.
Kripke, S. 1975. Outline of a theory of truth. Journal of Philosophy 72: 670–716.
Lachlan, A. 1981. Full satisfaction classes and recursive saturation. Canadian Mathematical Bulletin 24: 295–297.
Leigh, G.E. 2015. Conservativity for theories of compositional truth via cut elimination. The Journal of Symbolic Logic 80: 845–865.
Łełyk, M., and B. Wcisło. 2017a. Models of weak theories of truth. Archive for Mathematical Logic 56: 453–474.
Łełyk, M., and B. Wcisło. 2017b. Notes on bounded induction for the compositional truth predicate. Review of Symbolic Logic 10: 455–480.
Mancosu, P. 1998. From Brouwer to Hilbert the debate on the foundations of mathematics in the 1920s. Oxford/New York: Oxford University Press.
Parsons, C. 1971. Ontology and mathematics. The Philosophical Review 80: 151–176.
Parsons, C. 1974. Sets and classes. Noûs 8: 1–12.
Parsons, C. 2002. Realism and the debate on impredicativity. 1917–1944. In Reflections on the foundations of mathematics, Lecture notes in logic 15, ed. W. Sieg, R. Sommer, and C. Talcott, 372–389. Natick: ASL and A.K.Peters.
Rathjen, M. 2016. Indefinitess in semi-intuitionistic set theories: on a conjecture of Feferman. Journal of Symbolic Logic 81: 742–754.
Russell, B. 1906. On somes difficulties in the theory of transfinite numbers and order type. The Proceedings of the London Mathematical Society 4: 29–53.
Russell, B. 1919. Introduction to mathematical philosophy. London: Allen and Unwin.
Schindler, T. 2018. Some notes and comprehension. The Journal of Philosophical Logic 47: 449–479.
Simpson, S. 1999. Subsystem of second order arithmetic. Berlin/Heidelberg: Allen and Unwin.
Strahm, T. 2000. Autonomous fixed point progressions and fixed point transfinite recursion. In Logic colloquium ’98, ed. S. Buss, P. Hájek, and P. Pudlák, 449–464. Association for Symbolic Logic.
Tait, W. 1983. Against intuitionism: constructive mathematics is part of classical mathematics. The Journal of Philosophical Logic 12: 449–479.
Tait, W. 1986. Truth and proof: The platonism of mathematics. Synthese 69: 341–370.
Tarski, A. 1944. The semantic conception of truth and the foundations of semantics. Philosophy and Phenomenological Research 4: 341–376.
Tarski, A. 1956. The concept of truth in formalized language. In Logic, Semantics, Metamathematics: Papers From 1923 to 1938, ed. J. Woodger, 152–278. Oxford: Clarendon Press.
Weyl, H. 1910. Über die Definitionen der mathematischen Grundbegriffe. In Gesammelte Abhandlungen vol.1, Mathematisch-naturwissenschaftliche Blätter 7:93–95/109–113, 298–304.
Acknowledgements
I would like to thank the anonymous referees for helpful comments and the editors of this volume, Stefano Boscolo, Gianluigi Oliveri and Claudio Ternullo for their determination in bringing the project of this volume to completion.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2022 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this chapter
Cite this chapter
Cantini, A. (2022). Truth and the Philosophy of Mathematics. In: Oliveri, G., Ternullo, C., Boscolo, S. (eds) Objects, Structures, and Logics. Boston Studies in the Philosophy and History of Science, vol 339. Springer, Cham. https://doi.org/10.1007/978-3-030-84706-7_12
Download citation
DOI: https://doi.org/10.1007/978-3-030-84706-7_12
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-84705-0
Online ISBN: 978-3-030-84706-7
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)





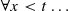 and ∃x < t… with < representing the standard ordering on natural numbers.
and ∃x < t… with < representing the standard ordering on natural numbers.