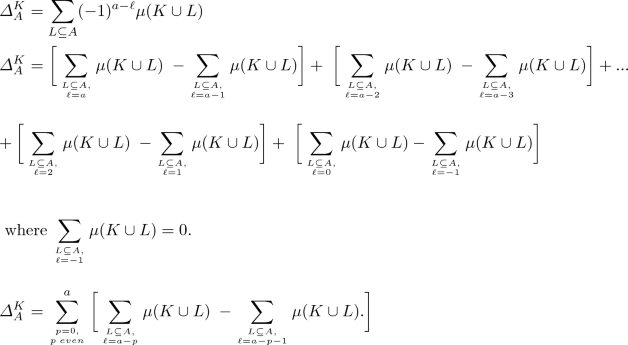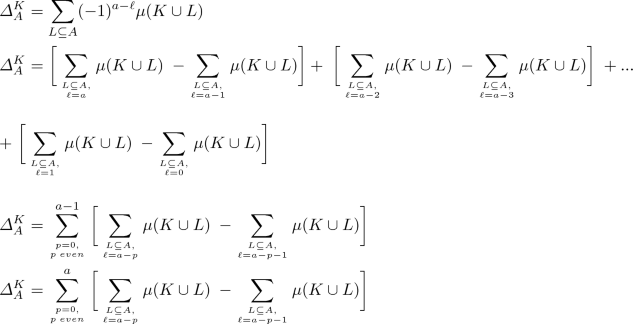Keywords

1 Introduction

In Multiple Criteria Decision Making (MCDM), the independence hypothesis of preferences is often considered to be restrictive. Thus, several other models that do not require the independence hypothesis have been developed, including the Choquet integral model. The Choquet integral model assumes that the criteria has been constructed so as to be commensurate. Here, we are not concerned with the commensurability hypothesis and therefore we assume that the criteria have been constructed to be commensurate.

In [6] we find two necessary and sufficient conditions for a preferential information on set of binary alternatives to be represented by a 2-additive Choquet integral model (i.e., a Choquet integral model using a 2-additive capacity). This result is extended by using a representation of the general model based on a set of generalized binary alternatives. We extend this result. Indeed, our first result gives a necessary and sufficient condition for preferential information on generalized binary alternatives to be representable by a general model of Choquet integral. In [5] it is proven that in the framework of binary alternatives, if the preferential information contains no indifference, and is representable by a 2-additive Choquet model, then we can choose among these representations one for which all Shapley interaction indices between two criteria are strictly positive. We extend also this result. Indeed, under the conditions of our first result, we shows that in the framework of generalized binary alternatives, if the preference information contains no indifference, it is always possible to represent it by a general Choquet integral model which all interaction indices are strictly positive.

This paper is organized as follows. After having recalled in the second section some basic elements on the model of the Choquet integral in MCDM, in the third section, we talk about of concept of necessary and possible interaction introduced in [5]. Then, in the fourth section, we expose our two results. Indeed, we begin by giving a necessary and sufficient condition for preferential information on the set of generalized binary alternatives containing no indifference to be represented by Choquet integral model. Under this condition, we show that it is always possible to represent this preferential information by a Choquet integral model where all interaction indices are strictly positive. We illustrate our results with an example, and we end with a conclusion.

2 Notations and Definitions

2.1 The Framework

Let X be a set of alternatives evaluate on a set of n criteria \(N = \{1, 2,...,n\}\). The set of all alternatives X is assumed to be a subset of a Cartesian product \( X_{1} \times X_{2}\times ...\times X_{n}\).

The criteria are recoded numerically using, for all \(i \in N,\) a function \(u_{i}\) from \(X_{i} \) into \(\mathbb {R}\). Using these functions allows to assume that the various recoded criteria are “commensurate” and, hence, the application of the Choquet integral model is meaningful [4].

For all \(x = (x_{1},...,x_{n}) \in X\), we will sometimes write u(x) as a shorthand for \((u_{1}(x_{1}),..., u_{n}(x_{n})).\)

We assume the DM is able to identify on each criterion \(i \in N\) two reference levels \(1_{i}\) and \(0_{i}\):

  • the level \(0_{i}\) in X is considered as a neutral level and we set \(u_{i}(0_{i}) = 0;\)

  • the level \(1_{i}\) in X is considered as a good level and we set \(u_{i}(1_{i}) = 1\).

For a subset \(S \subseteq N\) we define the element \(a_{S} = (1_{S}; 0_{-S}) \) of X such that \(a_{i} = 1_{i}\) if \(i \in S\) and \(a_{i} = 0_{i}\) otherwise. We suppose that for all \(S \subseteq N, \, a_{S} \in X\).

2.2 Choquet Integral

The Choquet integral [3] in an aggregation function known in MCDM as a tool generalizing the arithmetic mean. It is based on the notion of capacity \(\mu \) defined as a function from the powerset \(2^{N}\) into [0, 1] such that:

\(\mu (\emptyset ) = 0,\)

\(\mu (N) = 1, \)

\(\forall S, T \in 2^{N}, [S \subseteq T \Longrightarrow \mu (S) \le \mu (T)] \) (monotonicity).

For an alternative \(x = (x_{1},...,x_{n}) \in X\), the expression of the Choquet integral w.r.t. a capacity \(\mu \) is given by:

$$\begin{aligned} C_{\mu }(u(x))&= C_{\mu }(u_{1}(x_{1}),..., u_{n}(x_{n})) \\&=\displaystyle \sum _{i=1}^{n}\bigg [u_{\sigma (i)}(x_{\sigma (i)}) - u_{\sigma (i-1)}(x_{\sigma (i-1)}) \bigg ] \mu (\{\sigma (i),...,\sigma (n)\}) \end{aligned}$$

Where \(\sigma \) is a permutation on N such that \( u_{\sigma (1)}(x_{\sigma (1)}) \le u_{\sigma (2)}(x_{\sigma (2)}) \le ...\le u_{\sigma (n)}(x_{\sigma (n)}) \) and \(u_{\sigma (0)}(x_{\sigma (0)}) = 0.\)

Our work is based on the set \(\mathcal {B}\) defined as following.

Definition 1

The set of generalized binary alternatives is defined by \( \mathcal {B} = \{a_{S} = (1_{S}, 0_{-S}) : S \subseteq N \}.\)

Remark 1

For all \( S \subseteq N\), we have \( C_{\mu }(a_{S}) = \mu (S). \)

The idea is to ask to the DM its preferences by comparing some elements of \( \mathcal {B}\). We obtain the binary relations P and I defined as follows.

Definition 2

An ordinal preference information \(\{P, I \}\) on \( \mathcal {B}\) is given by:

  • \(P = \{(x, y) \in \mathcal {B} \times \mathcal {B} \): DM strictly prefers x to \(y\},\)

  • \(I = \{(x, y) \in \mathcal {B} \times \mathcal {B} \): DM is indifferent between x and \(y\}.\)

We add to this ordinal preference information a relation M modeling the monotonicity relations between binary alternatives, and allowing us to ensure the satisfaction of the monotonicity condition \( [ S \subseteq T \; \Longrightarrow \mu (S) \le \mu (T)] \).

Definition 3

For all \( a_{S}, a_{T} \in \mathcal {B}, \; a_{S}Ma_{T}\) if [\(not(a_{S}(P \cup I)a_{T}) \) and \(S \supseteq T\)].

Remark 2

\(a_{S}Ma_{T} \Longrightarrow C_{\mu }(a_{S}) \ge C_{\mu }(a_{T})\).

Definition 4

There exists a strict cycle of \( (P \cup M)\) if there exists the elements \(x_{0}, x_{1}..., x_{r}\) of \(\mathcal {B}\) such that \(x_{0} (P \cup M) x_{1}(P \cup M)...(P \cup M)x_{r}(P \cup M)x_{0}\) and for a least one \( i \in \{0, ..., r-1\}, \; x_{i}Px_{i+1}. \)

2.3 General Interaction Index

Definition 5

The general interaction [2] index w.r.t. a capacity \(\mu \) is defined by:

\( \forall A \subseteq N,\)

$$\begin{aligned} I_{A}^{\mu } = \displaystyle \sum _{K \subseteq N \setminus A} \frac{(n-k-a)!k!}{(n-a + 1)!}\displaystyle \sum _{L \subseteq A}(-1)^{a-\ell }\mu (K \cup L ) \end{aligned}$$

where \( \ell = \mid L \mid , \; k = \mid K \mid \) and \( a = \mid A \mid \ge 2\).

Remark 3

Given a capacity \(\mu \) and \( A \subseteq N,\) we can rewrite the general interaction index as follows

$$\begin{aligned} I_{A}^{\mu } = \displaystyle \sum _{K \subseteq N \setminus A} \frac{(n-k-a)!k!}{(n-a + 1)!}\varDelta _{A}^{K} \end{aligned}$$

where \(\ell = \mid L \mid , \; a = \mid A \mid \) and \(k = \mid K \mid \) with \( \varDelta _{A}^{K} = \displaystyle \sum _{L \subseteq A}(-1)^{a-\ell }\mu (K \cup L )\).

The following lemma gives a decomposition of \( \varDelta _{A}^{K}\) (we assume that 0 is an even number).

Lemma 1

\(\forall A \subseteq N, \, \forall K \subseteq N \setminus A\),

$$\begin{aligned} \varDelta _{A}^{K} = \displaystyle \sum _{p = 0, \atop p \; even} ^{a} \bigg [\displaystyle \sum _{L \subseteq A, \atop \ell =a-p}\mu (K \cup L ) \; - \displaystyle \sum _{L \subseteq A, \atop \ell =a-p-1}\mu (K \cup L )\bigg ]. \end{aligned}$$

Proof

We will reason according to the parity of a.

  • If a is even.

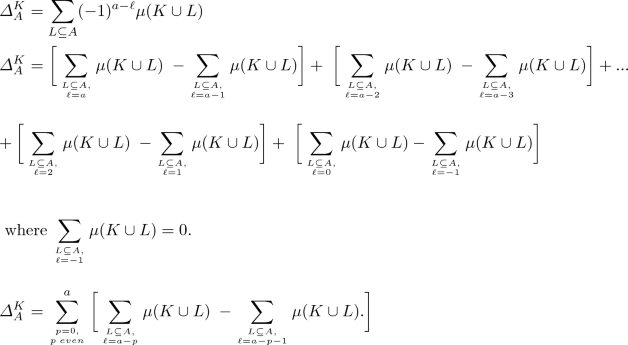
  • If a is odd.

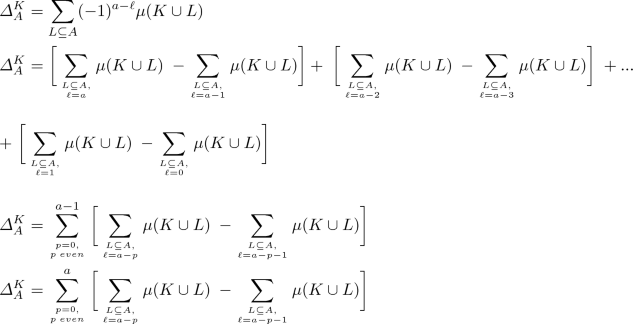
    since a is odd but p is even.

   \(\square \)

Remark 4

Let N be the set of criteria, \(A \subseteq N, \, K \subseteq N \setminus A \) and \(1 \le t \le a \). We have:

\( \displaystyle \sum _{ L \subseteq A, \atop \ell =t} \displaystyle \sum _{i \in L } \mu (K \cup L \setminus \{i\}) = C^{1}_{a-t+1}\displaystyle \sum _{ L \subseteq A, \atop \ell =t-1} \mu (K \cup L) \) where \(C_{n}^{p} = \dfrac{n!}{p!(n-p)!}.\)

Let us illustrate Remark 4 with this example.

Example 1

Let \( N = \{1, 2, 3, 4 \}, \, A = \{1, 2, 3\}\) and \( K \subseteq N \setminus A = \{4\} \). We have:

$$\begin{aligned} \displaystyle \sum _{ L \subseteq A, \atop \ell =2} \displaystyle \sum _{i \in L } \mu (K \cup L \setminus \{i\})&= \displaystyle \sum _{i \in \{1, 2\} } \mu (K \cup \{1, 2\} \setminus \{i\}) + \displaystyle \sum _{i \in \{1, 3\} } \mu (K \cup \{1, 3 \} \setminus \{i\}) \\ + \displaystyle \sum _{i \in \{2, 3 \} } \mu (K \cup \{2, 3\} \setminus \{i\}) \\&= 2\mu (K \cup \{1\}) + 2 \mu (K \cup \{2\}) + 2 \mu (K \cup \{3\}) \\&= 2 \displaystyle \sum _{ L \subseteq A, \atop \ell =1} \mu (K \cup L) \end{aligned}$$

with \( 2 = C^{1}_{3-2+1}\).

3 Necessary and Possible Interaction

Once the DM compares a number a alternatives in terms of strict preferences (P) or indifference (I), the following definition tells us when this ordinal preference information is representable by Choquet integral model.

Definition 6

An ordinal preference information \(\{P, I \} \) on \(\mathcal {B}\) is representable by a Choquet integral model if we can find a capacity \(\mu \) such that: For all \(S, T \subseteq N\),

  • \( a_{S} P a_{T} \Longrightarrow C_{\mu }(u(a_{S})) > C_{\mu }(u(a_{T})); \)

  • \( a_{S} I a_{T} \Longrightarrow C_{\mu }(u(a_{S})) = C_{\mu }(u(a_{T})). \)

The set of all capacities that can be used to represent the ordinal preference information \(\{P, I \}\) at hand will be denoted \(C_{Pref}(P, I).\) When there is no ambiguity on the underlying ordinal preference information, we will simply write \(C_{Pref}.\)

The following definition of necessary and possible interactions will be central in the rest of this text. This definition is given in [5].

Definition 7

Let A be a subset of N. We say that:

  1. 1.

    There exists a possible positive (resp. null, negative) interaction among the elements of A if there exists a capacity \(\mu \in C_{Pref} \) such that \(I_{A}^{\mu } > 0 \; (resp. \; I_{A}^{\mu } = 0, \; I_{A}^{\mu } < 0);\)

  2. 2.

    There exists a necessary positive (resp. null, negative) interaction among the elements of A if \(I_{A}^{\mu } > 0 \; (resp. \; I_{A}^{\mu } = 0, \; I_{A}^{\mu } < 0)\) for all capacity \( \mu \in C_{Pref}\).

Remark 5

Let be A a subset of criteria.

  • If there exists a necessary positive (resp. null, negative) interaction among the elements of A, then there exists a possible positive (resp. null, negative) interaction among the elements of A.

  • If there is no necessary positive (resp. null, negative) interaction among the elements of A, then there exists a possible negative or null (resp. positive or negative, positive or null) interaction among the elements of A.

Let A be a subset of N and \(\{P, I \}\), an ordinal preference information. We can have a possible but not necessary interaction, what makes the interpretation difficult because dependent on the capacity chosen into \(C_{Pref}(P,I)\). Indeed, the interpretation of the interaction only makes sense in the case of the necessary interaction.

4 Results

The following proposition gives a necessary and sufficient condition for an ordinal preference information on \(\mathcal {B}\) containing no indifference to be representable by a Choquet integral model.

Proposition 1

Let \(\{P, I\}\) be an ordinal preference information on \(\mathcal {B}\) such that \(I = \emptyset \).

\(\{P, I \}\) is representable by a Choquet integral if and only if the binary relation \((P\cup M)\) contains no strict cycle.

Proof

Necessity. Suppose that the ordinal preference information \(\{P, I \}\) on \(\mathcal {B}\) is representable by a Choquet integral. So there exists a capacity \(\mu \) such that \(\{P, I \}\) is representable by \(C_{\mu }\).

If \(P\cup M\) contains a strict cycle, then there exists \(x_{0}, x_{1},...,x_{r}\) on \(\mathcal {B}\) such that

\(x_{0}(P\cup M)x_{1}(P \cup M)...(P \cup M)x_{r}(P \cup M)x_{0}\) and there exists \( x_{i}, x_{i + 1} \in \{x_{0}, x_{1},..., x_{r}\} \) such that \( x_{i} P x_{i + 1}.\) Since \(\{P, I \}\) is representable by \(C_{\mu }\), therefore \(C_{\mu }(x_{0}) \ge ...\ge C_{\mu }(x_{i}) > C_{\mu }(x_{i + 1}) \ge ...\ge C_{\mu }(x_{0}) \), then \(C_{\mu }(x_{0}) > C_{\mu }(x_{0}).\) Contradiction.

So, \(P \cup M\) contains no strict cycle.

Sufficiency. Assume that \((P \cup M) \) contains no strict cycle, then there exists \(\{\mathcal {B}_{0}, \mathcal {B}_{1},...,\mathcal {B}_{m} \}\) a partition of \( \mathcal {B}\), builds by using a suitable topological sorting on \((P\cup M)\) [1].

We construct a partition \(\{\mathcal {B}_{0}, \mathcal {B}_{1},...,\mathcal {B}_{m} \}\) as follows:

\(\mathcal {B}_{0} = \{ x \in \mathcal {B} : \forall y \in \mathcal {B}, not [ x(P \cup M)y]\}, \)

\(\mathcal {B}_{1} = \{ x \in \mathcal {B}\setminus \mathcal {B}_{0} : \forall y \in \mathcal {B}\setminus \mathcal {B}_{0}, not [ x(P \cup M)y]\}, \)

\(\mathcal {B}_{i} = \{ x \in \mathcal {B}\setminus (\mathcal {B}_{0} \cup ...\cup \mathcal {B}_{i-1}) : \forall y \in \mathcal {B}\setminus (\mathcal {B}_{0} \cup ...\cup \mathcal {B}_{i-1}), not [ x(P \cup M)y]\}, \) for all \( i=1;2;...;m.\)

Let us define the map** \(f : \mathcal {B} \longrightarrow \mathbb {R}\) and \(\mu : 2^{N} \longrightarrow [0, 1]\) as follows: for \(\ell \in \{0, 1, ..., m \},\)

\( \forall x \in \mathcal {B}_{\ell },\) \( f(\phi (x)) = \left\{ \begin{array}{l} 0 \;\;\; if \;\;\; \ell =0, \\ (2n)^{\ell } \;\;\; if \; \; \; \ell \in \{1, 2, ...,m \}. \end{array} \right. \)

\(\mu (S) = \frac{f_{S}}{\alpha }\), where \(f_{S} = f(\phi (a_{S})) \) and \( \alpha = f_{N} = (2n)^{m}.\)

Let \(a_{S}, a_{T} \in \mathcal {B}\) such that \(a_{S}Pa_{T}\). Show that \(C_{\mu }(a_{S}) > C_{\mu }(a_{T}).\)

As \(I = \emptyset \), then \(\mathcal {B}_{0} = \{a_{0}\} \) and \(\mathcal {B}_{m} = \{a_{N}\}. \)

  • If \(T = \emptyset \), then \(a_{T} \in \mathcal {B}_{0}\) and \(a_{S} \in \mathcal {B}_{r}\) with \(r \ge 1\).

    We have \( C_{\mu }(a_{S}) = \dfrac{(2n)^{r}}{\alpha } > 0 = \mu (\emptyset ) = C_{\mu }(a_{T}). \)

  • If \( \emptyset \subsetneqq T \), since \(a_{S}, a_{T} \in \mathcal {B}\), and \(\{\mathcal {B}_{0}, \mathcal {B}_{1},...,\mathcal {B}_{m} \}\) is a partition of \( \mathcal {B}\) (with \( \mathcal {B}_{0} = \{a_{0}\} \) ), then there exists \(r, q \in \{ 1, ..., m\} \) such that \( a_{S} \in \mathcal {B}_{r}, \; a_{T} \in \mathcal {B}_{q}\).

    Therefore \( C_{\mu }(a_{S}) = \mu (S) = \dfrac{f_{S}}{\alpha } = \dfrac{(2n)^{r}}{\alpha }, \; C_{\mu }(a_{T}) = \mu (T) = \dfrac{f_{T}}{\alpha } = \dfrac{(2n)^{q}}{\alpha }.\)

    Moreover \(a_{S}Pa_{T}\), then \(r > q\), so \((2n)^{r} > (2n)^{q}\), therefore \( \dfrac{(2n)^{r}}{\alpha } > \dfrac{(2n)^{q}}{\alpha }\), i.e., \(C_{\mu }(a_{S}) > C_{\mu }(a_{T}). \)

In both cases, \(C_{\mu }(a_{S}) > C_{\mu }(a_{T}). \) Therefore \(\{P, I\}\) is representable by \(C_{\mu }\).    \(\square \)

Given the ordinal preference information \(\{P, I\}\) on \(\mathcal {B},\) under the previous conditions, the following proposition shows that: it is always possible to choose in \(C_{Pref}(P,I)\), one capacity allowing all the interaction indices are strictly positive. This result shows that positive interaction is always possible into all subsets of criteria in general Choquet integral model.

Proposition 2

Let \(\{P, I \}\) be an ordinal preference information on \(\mathcal {B}\) such that \(I = \emptyset \), and \( (P \cup M) \) containing no strict cycle.

There exists a capacity \(\mu \) such that \(\mathcal {C}_{\mu }\) represents \(\{P, I \}\) and for all \( A \subseteq N, I_{A}^{\mu } > 0. \)

Proof

To show that \(I_{A}^{\mu } > 0\), we will prove that for all \( K \subseteq N \setminus A, \; \displaystyle \sum _{L \subseteq A}(-1)^{a-\ell }\mu (K \cup L ) > 0.\)

The partition \(\{\mathcal {B}_{0},...,\mathcal {B}_{m}\}\) of \( \mathcal {B}\) and the capacity \(\mu \) are built as in proof of Proposition 1. Since \(I = \emptyset \), then we have \( \mathcal {B}_{0} = \{a_{0}\} \) and \( \mathcal {B}_{m} = \{a_{N}\}. \)

Consider capacity \(\mu \) define by: \(\mu (S) = \frac{f_{S}}{\alpha }\), where \(f_{S} = f(\phi (a_{S})) \) and \( \alpha = f_{N} = (2n)^{m}.\)

Let \(K \subseteq N \setminus A\). According to the previous Lemma 1 we have

\( \displaystyle \sum _{L \subseteq A}(-1)^{a-\ell }\mu (K \cup L ) = \displaystyle \sum _{p = 0, \atop p \; even} ^{a} \bigg [\displaystyle \sum _{L \subseteq A, \atop \ell =a-p} \mu (K \cup L ) \; - \displaystyle \sum _{L \subseteq A, \atop \ell =a-p-1}\mu (K \cup L )\bigg ] \)

Let \( L \subseteq A, \; \mid L \mid = a-p\) with \( p \in \{0, 1, ..., a\}\) and even number.

As \( K \cup L \supsetneqq K \cup L \setminus \{i\}\) for all \(i \in L\), then \( a_{K \cup L}(P\cup M)a_{K \cup L \setminus \{i\}}\), hence there exists \( q \in \{1, 2,...,m \}\) such that \( a_{K \cup L} \in \mathcal {B}_{q}\) and \(\forall i \in L, \) there exists \( r_{i} \in \{0, 1, 2, ..., m\} \) such that \( a_{K \cup L\setminus \{i\}} \in \mathcal {B}_{r_{i}}\) with \(r_{i} \le q-1\).

Fig. 1.
figure 1

An illustration of the elements \(\mathcal {B}_m\), \(\mathcal {B}_q\), \(\mathcal {B}_{r_{i}}\), and \(\mathcal {B}_0\) such that \(m>q>r_{i} > 0\) with \(i \in N\).

Full size image

Then \(\mu (K \cup L) = (2n)^{q} = (2n)(2n)^{q-1}. \)

\(\displaystyle \sum _{i \in L } \mu (K \cup L \setminus \{i\}) = \displaystyle \sum _{i \in L }(2n)^{r_{i}} \le \displaystyle \sum _{i \in L }(2n)^{q-1} = l(2n)^{q-1} \)

As \( 2n > l,\) then \(\mu (K \cup L) > \displaystyle \sum _{i \in L } \mu (K \cup L \setminus \{i\}) \) , hence \( \displaystyle \sum _{L \subseteq A, \atop l = a-p} \mu (K \cup L) > \displaystyle \sum _{ L \subseteq A, \atop l=a-p} \displaystyle \sum _{i \in L } \mu (K \cup L \setminus \{i\}) \) According to Remark 4 (with \( t = a-p\)), we have

\( \displaystyle \sum _{ L \subseteq A, \atop \ell =a-p} \displaystyle \sum _{i \in L } \mu (K \cup L \setminus \{i\}) = C^{1}_{p+1}\displaystyle \sum _{ L \subseteq A, \atop \ell =a-p-1} ^{a} \mu (K \cup L) > \displaystyle \sum _{ L \subseteq A, \atop \ell =a-p-1} ^{a} \mu (K \cup L)\) since \(C^{1}_{p+1} = p+1 > 1. \)

So \( \displaystyle \sum _{L \subseteq A, \atop \ell =a-p}\mu (K \cup L ) > \displaystyle \sum _{L \subseteq A, \atop \ell =a-p-1}\mu (K \cup L ), \) i.e., \( \displaystyle \sum _{L \subseteq A, \atop \ell \!=\!a-p}\mu (K \cup L )\! -\! \displaystyle \! \sum _{L \subseteq A, \atop \ell =a-p-1}\mu (K \cup L )\! >\! 0.\)

We then have \( \displaystyle \sum _{p=0, \atop p \; even}^{a} \bigg [ \displaystyle \sum _{L \subseteq A, \atop \ell =a-p}\mu (K \cup L ) - \displaystyle \sum _{L \subseteq A, \atop \ell =a-p-1}\mu (K \cup L ) \bigg ] > 0. \)

We have just proved that For all \( K \subseteq N \setminus A, \; \displaystyle \sum _{L \subseteq A}(-1)^{a-\ell }\mu (K \cup L ) > 0 \).

We can therefore conclude that \(I_{A}^{\mu } > 0. \)    \(\square \)

The following example illustrates our two results.

Example 2

\(N = \{1, 2, 3, 4 \}, \; P = \{(a_{23}, a_{1}), (a_{234}, a_{123}), (a_{2}, a_{13})\}\).

The ordinal preference information \(\{P, I\}\) contains no indifference and the binary relation \((P\cup M)\) contains no strict cycle, so \(\{P, I \}\) is representable by a Choquet integral model.

A suitable topological sorting on \((P \cup M) \) is given by:

\(\mathcal {B}_{0} = \{a_{0}\}\); \( \mathcal {B}_{1} = \{a_{1}, a_{3}, a_{4}\}; \) \( \mathcal {B}_{2} = \{a_{13}, a_{14}, a_{34}\}\); \( \mathcal {B}_{3} = \{a_{2}\}\); \( \mathcal {B}_{4} = \{a_{12}, a_{23}, a_{24}\}\);

\( \mathcal {B}_{5} = \{a_{123}, a_{124}, a_{134}\}\); \( \mathcal {B}_{6} = \{a_{234}\} \) and \( \mathcal {B}_{7} = \{a_{N}\} \).

The ordinal preference information \(\{P, I\} \) is representable by a following capacity \(\mu \):

S

\(\emptyset \)

{1}

{2}

{3}

{4}

{1, 2}

{1, 3}

{1, 4}

{2, 3}

{2, 4}

{3, 4}

{1, 2, 3}

{1, 2, 4}

{1, 3, 4}

{2, 3, 4}

N

\(8^{7} \times \mu (S)\)

0

8

\( 8^{3} \)

8

8

\( 8^{4} \)

\( 8^{2} \)

\( 8^{2} \)

\( 8^{4} \)

\( 8^{4} \)

\( 8^{2} \)

\( 8^{5} \)

\( 8^{5} \)

\( 8^{5} \)

\( 8^{6} \)

\(8^{7}\)

Considering the previous capacity, the corresponding interaction indices are given by the following table:

A

{1, 2}

{1, 3}

{1, 4}

{2, 3}

{2, 4}

{3, 4}

{1, 2, 3}

{1, 2, 4}

{1, 3, 4}

{2, 3, 4}

N

\(8^{7} \times I^{\mu }_{A}\)

611.33

611.66

688.16

726.16

726.16

726.33

899

899

612.83

612.83

612.83

We can see that \(I^{\mu }_{A} > 0, \; \forall A \subseteq N\) such that \(\mid A \mid \ge 2\).

5 Conclusion

This article deals with the notion of interaction within a subset of criteria of any size, in the Choquet integral model. Our first result gives a necessary and sufficient condition for ordinal preference information on generalized binary alternatives to be representable by a general model of Choquet integral. This extends theorem 1, Page 305 [6].

Under condition of our first result, our second result shows that in the framework of generalized binary alternatives, if the ordinal preference information contains no indifference, it is possible to represent it by a general Choquet integral model which all Shapley interaction indices between a subset of criteria are strictly positive. This extends theorem 2, Page 10 [5].

The subject of this paper offer several avenues for future research. In fact, It would be interesting as in [5] to provide a linear program to test the necessary interaction outside the framework of generalized binary alternatives. Otherwise we will examine the case where \( I \ne \emptyset \). We are also interested in duality. Indeed, is it always possible to build a capacity relative to which all the interaction indices will be strictly negative? It would finally be interesting to study the case of bipolar scales. We are already investigating some of these research avenues.