Keywords

1 Introduction

The increasing penetration of Renewable Energy Sources (RES) leads to a power system operation closer to its operational limits. Enhanced methods and tools will be crucial for a secure, but also efficient and cheap planning and operation of the power grid. A Transmission System Operator (TSO) will have larger assets of controllable devices at hand, such as Voltage Source Converter (VSC-) based HVDC-systems and energy storage systems. Combined with the need to assure N-1 security, this requires a Security-Constrained Dynamic Optimal Power Flow (SC-D-OPF), which incorporates both N-1 security and multiple time steps into the optimization. First research in that area was done in [1], where not only power but also necessary energy reserves can be determined to ensure N-1 security. In [2], successive linear algorithms and approximated power flows are used to solve large-scale SC-D-OPF problems in a European context. The authors of [3] propose an SC-D-OPF model including uncertainty of wind power or equipment availability, which is solved in a two-stage stochastic program. In [4], SC-D-OPF is used as inner iteration in a hierarchical approach to optimize a central deployment signal which is sent to the units able to provide a reserve. Furthermore, [5,6,7] include energy storage systems in an SC-D-OPF calculation. A further extension is shown in [8], where SC-D-OPF is solved in a hybrid AC-DC grid with energy storage.

Due to the increasing complexity of the power system and an operation closer to network limitations, central coordination in large scale networks comes with major computational burdens. Furthermore, privacy can be a concern for each transmission system operator (TSO) controlling a certain region. Subsequently, the interest in distributed optimization, also referred to as multi-area optimization has substantially grown in recent years. An early overview of distributed OPF algorithms can be found in [9] and the most recent developments are examined in detail in [10]. The Alternating Direction of Multipliers Method (ADMM) [11], has become a popular branch to tackle the non-convex AC OPF problem [12,13,14]. Each area uses variable duplicates from neighboring areas and is solved to optimality. Penalty terms, which are calculated from the coupling variable deviation and Lagrangian multipliers, are added to the objective function to push two neighbors towards a common boundary solution. ADMM was applied to a hybrid AC-DC grid in [15]. Multi-area optimization is applied to D-OPF with storage in [16] using OCD, but to the best of our knowledge, no attempts have been made toward distributing SC-D-OPF.

2 Security-Constrained Dynamic Optimal Power Flow (SC-D-OPF)

The optimization horizon is defined by a set of time steps \(\mathcal T = \{1,\ldots ,T\}\) with T the total number of considered time steps. Furthermore, we define a scenario set \(\mathcal C=\{0,\ldots ,C\}\). Here, scenario c = 0 defines the base case, i.e. the original fault-free network. A total of C possible contingencies is added by including modified versions of the base case to the scenario set. A modification could be the outage of an AC line, a DC line or a converter. With x t, c the optimization variables of time step t and scenario c, the full set of optimization variables is collected in

$$\displaystyle \begin{aligned} x=\big((x^{1,0})^\top,\ldots,(x^{1,C})^\top,\ldots,(x^{T,0})^\top,\ldots,(x^{T,C})^\top\big)^\top. \end{aligned} $$
(1)

The full problem has the form (2):

$$\displaystyle \begin{aligned} \underset{x}{\text{minimize}} & \quad \sum_{t\in\mathcal{T}} \sum_{c\in\mathcal{C}} p^{t,c} \cdot f(x^{t,c}) \end{aligned} $$
(2a)
$$\displaystyle \begin{aligned} \text{subject to} & \quad h_{\text{base}}(x^{t,c})\leq 0 \quad \forall t\in\mathcal{T},c\in\mathcal{C} \end{aligned} $$
(2b)
$$\displaystyle \begin{aligned} & \quad h_{\text{dyn}}(x^{t,0},x^{t-1,0})\leq 0 \quad \forall t\in\mathcal{T}\setminus 1 \end{aligned} $$
(2c)
$$\displaystyle \begin{aligned} & \quad h_{\text{N-1}}(x^{t,0},x^{t,c})\leq 0 \quad \forall t\in\mathcal{T},c\in\mathcal{C}\setminus 0 . \end{aligned} $$
(2d)

It minimizes the sum of weighted costs f over all scenarios. Factor p t, c defines a probability of each contingency to enable a risk-based OPF. Constraints h base describe the basic constraints of a conventional OPF, which must be fulfilled during each scenario (t, c). That includes AC and DC node power balance; thermal AC and DC branch limits; AC and DC voltage limits; quadratic loss function of AC-DC converters; and operational limits of generators, converters or sheddable loads. Time-dependent constraints, such as storage energy limits or generator ram** limits, are collected in h dyn. Those constraints only apply to the base case (c = 0), since set points after an outage are coupled solely to the respective base case of the identical time step. This N-1 coupling is modeled by the constraints h N-1 and guarantees N-1 security. Here, the coupling between each contingency and the base case is explicitly modeled. That is, set point deviation limits from before to after the occurrence of an outage can be defined. Note that for the sake of readability, we omit equality constraints which can be interpreted as reformulated inequalities as well. We refer to [8] for more details on the modeling.

3 Distributed Formulation

For the sake of readability, we write (2) in the form (3):

$$\displaystyle \begin{aligned} \underset{x}{\text{minimize}} & \quad f(x) \end{aligned} $$
(3a)
$$\displaystyle \begin{aligned} \text{subject to} & \quad h(x)\leq 0. \end{aligned} $$
(3b)

Let R non-overlap** regions be defined in \(\mathcal {R}=\{1,\ldots ,R\}\), that is, each node belongs to exactly one region. An equivalent problem as (3), but in separable form, can be written as (4):

$$\displaystyle \begin{aligned} \underset{x_k,\forall k\in\mathcal R}{\text{minimize}} & \quad \sum_{k\in\mathcal{R}} f_k(x_k) {} \end{aligned} $$
(4a)
$$\displaystyle \begin{aligned} \text{subject to} &\quad h_k(x_k)\leq 0, \quad \forall k\in\mathcal{R} {} \end{aligned} $$
(4b)
$$\displaystyle \begin{aligned} &\quad \sum_{k\in \mathcal R^{}} A_k x_k =0.{} \end{aligned} $$
(4c)

Here, \(x_k\in \mathbb {R}^{l_k}\), \(h_k: \mathbb {R}^{l_k} \rightarrow \mathbb {R}^{m_k}\) and \(f_k: \mathbb {R}^{l_k} \rightarrow \mathbb {R}\) are optimization variables, non-linear constraints and objective function, respectively, in a region k. Matrix \(A_k \in \mathbb {R}^{n \times l_k}\) maps x k onto the full set of n coupling constraints and enforces consensus between regions. Thus, (4b) forms independent local SC-D-OPF constraints and (4c) form the coupling constraints which recuperate a feasible overall power flow.

4 Network Decomposition in AC-DC Grids

To allow for a separable formulation, the network is first partitioned and then decomposed.

Network partitioning can be crucial for distributed algorithms to achieve good performance. We believe that network partitions are inherently given by structural responsibilities. For example, a region or control area could represent one TSO, multiple TSOs or a whole country. Thus, the number and dimension of AC regions are historically known. However, responsibilities in overlaying DC networks are yet to be defined and various options are thinkable [15]. We choose a Shared-DC approach. Here, we define R = R AC hybrid AC-DC regions, where each AC region may also contain DC nodes. Thus, each existing TSO gains control over converters in its own control area. Let \(\mathcal N_k\) identify all nodes in region k. Herewith, \(\mathcal N^{\text{AC}}_k\) collects all AC nodes and \(\mathcal N^{\text{DC}}_k\) all DC nodes in region k.

4.1 Decoupling of AC or DC Tie Line

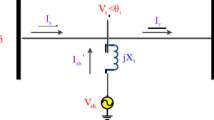
In principle, the decoupling of AC and DC tie line is identical, except for extended consensus constraints due to complex voltage and power in the AC case (Fig. 1).

Fig. 1
figure 1

Decoupling model of a tie line (AC or DC) between nodes i and j. Two auxiliary nodes (m and n) and two auxiliary generators (a and b) are added at the middle. Reactive power source Q G is only added for an AC tie line

Full size image

The original line is cut into two halves; auxiliary nodes (m, n) and auxiliary generators (a, b) are added at both open ends. Thus, node sets are augmented to \(\mathcal {N}_A\gets \{\mathcal {N}_A, m\}\), \(\mathcal {N}_B\gets \{\mathcal {N}_B, n\}\). To guarantee a feasible power flow, the voltage must be equal at nodes m and n. Furthermore, the generators must produce the same amount of power of the opposite sign. In the case of an AC tie line (\(i\in \mathcal {N}^{\text{AC}}_A, j\in \mathcal {N}^{\text{AC}}_B\)), this leads to boundary conditions including complex voltage and both active and reactive power. For time step and scenario (t, c), we have:

$$\displaystyle \begin{aligned} |V_{\text{AC,}m}^{t,c}|&=|V_{\text{AC,}n}^{t,c}| {} \end{aligned} $$
(5a)
$$\displaystyle \begin{aligned} \angle V_{\text{AC,}m}^{t,c}&=\angle V_{\text{AC,}n}^{t,c} {} \end{aligned} $$
(5b)
$$\displaystyle \begin{aligned} P_{\text{G,}a}^{t,c}&=-P_{\text{G,}b}^{t,c} \end{aligned} $$
(5c)
$$\displaystyle \begin{aligned} Q_{\text{G,}a}^{t,c}&=-Q_{\text{G,}b}^{t,c}. \end{aligned} $$
(5d)

In the case of a DC tie line (\(i\in \mathcal {N}^{\text{DC}}_A, j\in \mathcal {N}^{\text{DC}}_B\)), only real voltage and active power must meet the constraints. For time step and scenario (t, c), we have:

$$\displaystyle \begin{aligned} V_{\text{DC,}m}^{t,c}&=V_{\text{DC,}n}^{t,c} \end{aligned} $$
(6a)
$$\displaystyle \begin{aligned} P_{\text{G,}a}^{t,c}&=-P_{\text{G,}b}^{t,c}. \end{aligned} $$
(6b)

Equations (5) and (6) are the only boundary constraints.

Fig. 2
figure 2

Schematic problem decomposition for two areas (blue and green) under consideration of three time steps and two contingencies. A dashed box represents an optimization problem. (a) Centralized SC-D-OPF. (b) Distributed SC-D-OPF

Full size image

4.2 Building Consensus Constraint Matrix A

Since \(x_k^{t,c}\) uses the augmented node sets of region k, the auxiliary generator variables are included. Thus, consensus constraints (5)–(6) between region A and B can be written to

$$\displaystyle \begin{aligned} \tilde{A}_A^{t,c} x^{t,c}_{\text{A}} + \tilde{A}_B^{t,c} x^{t,c}_{\text{B}} = 0. \end{aligned} $$
(7)

This must be fulfilled for every considered time or contingency scenario (Fig. 2). Then we have

$$\displaystyle \begin{aligned} \begin{bmatrix} \tilde{A}_A^{1,0} & & & \tilde{A}_B^{1,0} & & \\ & \ddots & & & \ddots & &\\ & &\tilde{A}_A^{T,C} & & & \tilde{A}_B^{T,C} \end{bmatrix}\begin{bmatrix} x_{\text{A}}^{1,0} \\ \vdots \\ x_{\text{A}}^{T,C} \\ x_{\text{B}}^{1,0} \\ \vdots \\ x_{\text{B}}^{T,C} \end{bmatrix} = 0. {}\end{aligned} $$
(8)

In a more compact form, (8) can be written as

$$\displaystyle \begin{aligned} \sum_{k\in\{A,B\}} A_k x_k =0. \end{aligned} $$
(9)

5 Implemented ADMM Algorithm

The general idea of ADMM, see also [11], is the following. Augmented regional OPFs are solved and the deviation of boundary variables from a fixed auxiliary variable z, which is information stemming from neighboring regions, is penalized. The regions then exchange information and z is updated. The update is re-distributed to the local agents (areas) for a new OPF calculation until consensus between regions is achieved. It is constructed an augmented Lagrangian of the form

$$\displaystyle \begin{aligned} \mathcal{L}(x,z,\lambda) &= \sum_{k\in \mathcal R} \bigg\{ f_k(x_k)+\lambda^\top_k {A}_k (x_k-z_k) \notag\\ &+ \frac{\rho}{2}||{A}_k (x_k-z_k)||{}^2_{W} \bigg\} ,{} \end{aligned} $$
(10)

with penalty parameter \(\rho \in \mathbb {R}\). Dual variables of the consensus constraints are denoted with \(\lambda _k \in \mathbb {R}^{n\times 1}\), and \(W \in \mathbb {R}^{n\times n}\) is a positive definite, diagonal weighting matrix,Footnote 1 where each entry is related to one coupling constraint. We refer to W(S) if the entry is related to a power variable, and to W(V ) if the entry is related to a voltage variable. In ADMM literature, W is the identity matrix. The main steps during one iteration of the solving process are

$$\displaystyle \begin{aligned} 1.& \hspace{.5em} x = \text{argmin}_{x\in\mathcal{X}} \hspace{.5em} \mathcal{L}(x,z,\lambda){} \end{aligned} $$
(11a)
$$\displaystyle \begin{aligned} 2.& \hspace{.5em} z = \text{argmin}_{z\in\mathcal{Z}} \hspace{.5em}\mathcal{L}(x,z,\lambda){} \end{aligned} $$
(11b)
$$\displaystyle \begin{aligned} 3.& \hspace{.5em} \lambda\gets \lambda+\rho WA(x-z){} \end{aligned} $$
(11c)

with \(z = [z_1^\top \hspace{.5em} \ldots \hspace{.5em} z_R^\top ]^\top \). The first step (11a) minimizes a non-linear problem, where constraint region

$$\displaystyle \begin{aligned} \mathcal{X}=\left\{x | h_k(x_k)\leq 0, \forall k\in\mathcal{R}\right\} \end{aligned} $$
(12)

enforces local constraints (4b). Since z is fixed, (11a) is in fact a series of R independent problems which can be calculated in parallel. The second step minimizes a coupled quadratic problem, where

$$\displaystyle \begin{aligned} \mathcal{Z}=\left\{z | \sum_{k\in \mathcal R} A_k z_k =0\right\}{} \end{aligned} $$
(13)

enforces consensus of auxiliary variables z. In fact, (11b) calculates the average value between two consensus variables of neighboring regions [11, 13] and the problem can be reduced to

$$\displaystyle \begin{aligned} z = \text{argmin}_{z\in\mathcal{Z}} \hspace{.5em} \sum_{k\in \mathcal R} \frac{\rho}{2}||{A}_k (x_k-z_k)||{}^2_W. {} \end{aligned} $$
(14)

The weighting factors ρ and W can be neglected in (14), if the same weight is assigned to two coupled variables, which is a reasonable choice. Once a region has gathered necessary neighbor information, this step can be calculated locally as well [12]. In the third step (11c), dual variables are updated based on a weighted distance between x and z. Again, with given local x k and z k, each region can calculate λ k independently (Fig. 3).

Fig. 3
figure 3

Test system with embedded HVDC, energy storage and RES. Partitioning into 3 control areas

Full size image

In ADMM, an update rule on ρ can be useful to enforce consensus. A \(\rho _k\in \mathbb {R}\) is assigned to each region, which can be increased depending on the local residual, see (18b). If the residual has not decreased sufficiently compared to the previous iteration (indicator \(0<\varTheta \in \mathbb {R}<1\)), the penalty is increased by a constant factor of \(\tau \in \mathbb {R}>1\). The penalty parameter must be chosen carefully since it is widely known to be crucial for good convergence behavior [17]. An overview of the implemented ADMM is given in Algorithm 1.

Algorithm 1 ADMM

6 Results

6.1 Test Scenario

We use the illustrative AC-DC test system from [15], see Tables 1 and 2 for line and generator parameters, respectively. The generator at Node 5 is interpreted as a wind park and a PV park is connected to Node 3. RES upper power limit and load are variable over time. Forecast power profiles are taken from the Belgian transmission system operator Elia, which provides detailed RES generation and load data on its website. Adapted profiles for usage in the 5-bus test system are shown in Figs. 6 and 7. We assume quadratic generator cost functions as in [18] (see Table 3) and one cost coefficient for all reactive power injections. RES power injection is prioritized by assigning a low fuel price. Two energy storage systems with characteristics from Table 4 are connected to Node 3 and 5, respectively. Line flow limits of 400 MVA for Line 1–2 and 240 MVA for Line 4–5, respectively, are used. Furthermore, the capacity of each VSC is set to 200 MVA. Allowed voltage ranges lie between 0.9 and 1.1 pu on the AC side, and between 0.95 and 1.05 pu on the DC side.

Table 1 Line parameters with base power 100 MVA
Full size table
Table 2 Generator parameters. \(( \underline {P_{\text{G}}},\overline {P_{\text{G}}})\) in [MW] and \(( \underline {Q_{\text{G}}},\overline {Q_{\text{G}}})\) in [Mvar]
Full size table
Table 3 Generator cost coefficients
Full size table
Table 4 Parameters for each energy storage system
Full size table

6.2 Multi-area SC-D-OPF

To show applicability of the distributed approach to N-1 secure and dynamic OPF problems, a small example is presented in the following. An SC-D-OPF dispatch optimization is performed for the scenario set and \(\mathcal T=\{1,\ldots ,4\}\). Storages and VSCs are allowed curative control, that is, operating set points are allowed to move freely to a new set point after an outage. Contrarily, conventional generators are operated preventively, that is, the power set point must be valid both before and after the outage. However, to cope with changing system losses after an outage, a deviation of 1 % of installed capacity is allowed.

We use ADMM settings ρ = 500, τ = 1.02, Θ = 0.99, W(S) = 1 and W(V ) = 100.

General convergence behavior is shown in Fig. 4. Consensus error and objective suboptimality show similar behavior compared to conventional OPF cases. Consensus error (||Ax||∞) which depicts cross-border feasibility, falls below the threshold of 10−4 after 344 iterations. The deviation from centrally computed costs f ∗ is denoted with \(\tilde {f}=|1-f/f^*|\). The objective value error falls below 0.01 % when convergence is achieved.

The progress of storage variables is shown in Fig. 5 for all time steps after the outage. Dashed lines denote results from the centralized solution. Storage systems provide positive (ESS 2) and negative (ESS 1) power reserve after the outage. The amount of reserve is increased with time for a growing network stress level, but energy levels remain within limits. The distributed solution is represented by solid lines. Those oscillate around and eventually approach the target levels.

Fig. 4
figure 4

Convergence behavior of distributed SC-D-OPF in the 5-bus system with 4 time steps and 1 contingency. Left: consensus error, right: cost error. Both relative to central solution

Full size image
Fig. 5
figure 5

Convergence of storage power and energy levels after the outage

Full size image

7 Conclusion

This paper presents an approach to calculate SC-D-OPF in a distributed manner. That is, each control area computes a local N-1 secure and dynamic optimal dispatch which respects boundary constraints from neighboring areas for each time step and topology. After iteratively exchanging information and updating the local solution, a consensus is found which allows for a feasible cross-border power flow for all possible scenarios. Additionally, the result is close to the central optimal solution. Optimal curative storage or VSC set points can be determined for a contingency scenario which is in a foreign area. In this work, we apply the method to a small test system – the next steps are to increase system size, time horizon and number of contingencies.