1 Introduction

The generalized neural networks (GNNs) model, which is a combination of local field neural networks (LFNNs) and static neural networks (SNNs), has received increasing attention in recent years, due to the fact that it provides an unified frame for stability analysis of both SNNs and LFNNs [1–6]. It should be mentioned that back-propagation neural networks and optimization type neural networks can be modeled as SNNs, whereas Hopfield neural networks, bidirectional associative memory neural networks, and cellular neural networks can be modeled as LFNNs [6]. Therefore, it is enough to study the stability of GNNs instead of both LFNNs and SNNs. On the other hand, as a source of instability and poor performance, time-delays [7–9] always appear in many neural networks. Thus, stability analysis for delayed neural networks has received considerable attention over the past few decades [2–6, 10–35].

Since the time delays encountered in neural networks are usually not very long [2], delay-dependent criteria which include the information on the size of time delays are always less conservative than the delay-independent ones [2–6, 24–28, 30]. As is well known, the reduction of conservatism in delay-dependent stability criteria can be achieved from an a priori construction of LKF as well as the use of tighter bounding techniques to cope with its derivative. As far as the construction of LKFs is concerned, delay-slope-dependent LKFs [21], discretized LKFs [36], triple/four integral form LKFs [6, 27, 37, 38], delay-partitioning-dependent LKFs [26–28, 39] and augmented LKF [14, 40, 41] have already been introduced to reduce the conservativeness of the derived results. As to techniques for bounding the derivatives of LKFs, Jensen’s inequality [36], free-weighting matrices techniques [42], convex combination techniques [43], reciprocally convex combination (RCC) techniques [44], Peng-Park’s integral inequality [45], a Wirtinger-based integral inequality [30, 46], a free-matrix-based integral inequality [47], auxiliary function-based integral inequalities [48] and Bessel-Legendre integral inequality [49] are all indispensable bounding techniques/inequalities which play a crucial role in reducing the conservatism in delay-dependent stability criteria.

For stability analysis of GNNs with time-varying delay, the delay-dependent stability criteria have become a hot research topic in recent years [1–6]. In [1], delay-independent/-dependent stability criteria have been established by employing the LKF approach for GNNs with interval time-varying delays. Based on constructing a LKF including more information on activation functions and delay upper bounds, [2] has derived less conservative stability criteria for GNNs with two time-varying delay components. With a suitable augmented LKF and modified Wirtinger-based integral inequality, sufficient conditions for guaranteeing the asymptotic stability of the GNNs with time-varying delay are derived in terms of LMIs in [3]. By employing a new LKF and utilizing the free-matrix-based integral inequality [47] to bound the derivative of the LKF, less conservative stability criteria for GNNs with time-varying delay have been derived in [4]. Recently, by proposing an improved integral inequality to handle the cross-product terms occurred in the derivative of the LKF, [5] has achieved less conservative stability criteria for GNNs with interval time-varying delays via delay bi-partitioning method. More recently, by introducing an augmented LKF including triple and four integral terms, [6] has derived an improved delay-dependent stability criterion for GNNs with additive time-varying delays by the reciprocal convex combination technique. However, when revisiting the aforementioned literature, we find that these works still leave plenty of room for improvement because (a) the constructed LKFs do not contain adequate delay-partitioning augmented terms and (b) overbounding techniques are applied to estimate the derivatives of the LKFs, which are the origin of conservatism. As is well known, via a delay-partitioning approach, less and less conservative results can be expected as the fractioning becomes thinner [39]. To the best of the authors’ knowledge, [2, 5, 6] only adopt delay bi-partitioning method to analysis stability of GNNs, which means these results cannot be applied to the case when the delay interval is divided into multiple segments. Therefore, new stability criteria with less conservativeness for delayed GNNs in the frame of multi-partitioning delay approach combining with tighter bounding techniques/inequalities need to be urgently established, which is the main motivation of this paper.

Motivated by the above-mentioned discussion, the main objective of this paper is to develop less conservative stability criteria for GNNs with time-varying delay via tighter bounding inequalities and delay-partitioning approach. The main contributions of this paper are summarized as follows:

  • A newly augmented LKF is established by partitioning the delay in integral terms. And a \([P_{ij}]_{(m+1)\times(m+1)}\)-dependent sub-LKF is included in the augmented LKF, which enables the relationships between the augmented state vectors to be taken into full consideration.

  • A delay-partitioning-dependent triple integral term is included in the augmented LKF for the sake of reducing conservatism.

  • Some tighter bounding inequalities, i.e., the Wirtinger-based integral inequality, Peng-Park’s integral inequality and an auxiliary function-based integral inequality have been, respectively, employed to effectively handle the cross-product terms occurred in derivative of the LKF, which can contribute to less conservative stability criteria.

The rest of this paper is organized as follows. The main problem is formulated in Section 2 and improved stability criteria for the GNNs with time-varying delay are derived in Section 3. In Section 4, two numerical examples are provided; and a concluding remark is given in Section 5.

Notations

Through this paper, \(\mathbb{R}^{n}\) and \(\mathbb {R}^{n\times m} \) denote, respectively, the n-dimensional Euclidean space and the set of all \(n\times m\) real matrices; the notation \(A > ( \ge)\, B\) means that \(A - B\) is positive (semi-positive) definite; I (0) is the identity (zero) matrix with appropriate dimension; \(A^{\mathrm{T}}\) denotes the transpose; \(\operatorname{He}\{A\}\) represents the sum of A and \(A^{\mathrm{T}}\); \(\Vert \bullet \Vert \) denotes the Euclidean norm in \(\mathbb{R}^{n}\); ∗ denotes the elements below the main diagonal of a symmetric block matrix; \(C([ - \tau,0],\mathbb{R}^{n})\) is the family of continuous functions ϕ from interval \([ - \tau,0]\) to \(\mathbb{R}^{n}\) with the norm \(\Vert \phi \Vert _{\tau}= \sup_{ - \tau\le\theta\le0} \Vert {\phi(\theta)} \Vert \); let \(x_{t}(\theta)=x(t+\theta)\), \(\theta\in[ - \tau,0]\).

2 Problem statement and preliminaries

Consider the following GNN with time-varying delay and its equilibrium point being shifted to the origin [1]:

$$ \dot{x}(t)= - Ax(t)+ W_{1}f\bigl(W_{0}x(t) \bigr) + W_{2}f\bigl(W_{0}x\bigl(t -\tau(t)\bigr)\bigr), $$
(1)

where \(x(\cdot)=[x_{1}(\cdot), x_{2}(\cdot), \ldots, x_{n}(\cdot)]^{\mathrm {T}}\in\mathbb{R}^{n} \) is the neuron state vector; \(f(x(\cdot))=[f_{1}(x_{1}(\cdot)), f_{2}(x_{2}(\cdot)), \ldots, f_{n}(x_{n}(\cdot))]^{\mathrm{T}}\in\mathbb{R}^{n} \) denotes the neuron activation function; \(A=\operatorname{diag}\{a_{1}, a_{2}, \ldots, a_{n}\}\) is a diagonal matrix with \(a_{i}> 0\), \(i=1,2,\ldots,n\). \(W_{0}, W_{1}, W_{2} \in \mathbb{R}^{n \times n}\) are the connection weight matrices between neurons; the initial function for GNN (1) is \(\phi(t)\in C([ - \tau ,0],\mathbb{R}^{n})\); \(\tau(t)\) is a time-varying delay satisfying

$$\begin{aligned}& 0\leqslant\tau(t) \leqslant\tau, \end{aligned}$$
(2)
$$\begin{aligned}& \dot{\tau}(t) \leqslant\mu, \end{aligned}$$
(3)

where τ and μ are constants.

Assumption 1

([50])

The neuron activation functions \(f_{i}(\cdot)\) (\(i=1,2,\ldots, n\)) are continuous and bounded, and they satisfy

$$ k_{i}^{-}\leqslant \frac{{f_{i} (\alpha) - f_{i} (\beta)}}{{\alpha- \beta}} \leqslant k_{i}^{+} , \quad \forall\alpha,\beta \in R, \alpha\ne\beta, $$
(4)

where \(f_{i} (0)=0\), and \(k_{i}^{-}\), \(k_{i}^{+}\) (\(i=1,2,\ldots,n\)) are known real constants.

Remark 1

Assumption 1 on the activation function was originally proposed in [50], and such activation functions could be non-monotonic and more general than the usual sigmoid functions, since \(k_{i}^{-}\) and \(k_{i}^{+}\) may be positive, zero or negative. Furthermore, under Assumption 1, one has [21]:

  1. (i)

    for GNN (1) and any positive diagonal matrix T,

    $$ x^{\mathrm{T}}(t)W_{0}^{\mathrm{T}} K T K W_{0} x(t)-f^{\mathrm{T}}\bigl(W_{0} x(t)\bigr)Tf \bigl(W_{0} x(t)\bigr)\geqslant0, $$
    (5)

    where \(K=\operatorname{diag}\{k_{1}, k_{2},\ldots, k_{n}\}\), \(k_{i}=\max\{|k_{i}^{-}|, |k_{i}^{+}|\}\);

  2. (ii)

    for any \(\alpha,\beta\in R\),

    $$ \bigl[\bigl(f_{i} (\alpha) - f_{i} (\beta) \bigr)-k_{i}^{-}(\alpha-\beta)\bigr] \bigl[k_{i}^{+}( \alpha -\beta)-\bigl(f_{i} (\alpha) - f_{i} (\beta)\bigr) \bigr]\geqslant0; $$
    (6)

    and letting \(\beta=0\) in (6), it shows that

    $$ \bigl[f_{i} (\alpha) -k_{i}^{-} \alpha\bigr] \bigl[k_{i}^{+}\alpha-f_{i} (\alpha) \bigr]\geqslant0,\quad \forall\alpha\in R. $$
    (7)

Remark 2

It is worth noticing that the GNNs model (1) includes SNNs and LFNNs as its special cases [1]: (i) let \(W_{1} = I\), \(W_{2} = 0\), and \(W_{0} = W\), the GNNs model (1) reduces to the SNNs model; (ii) let \(W_{1} = W\), \(W_{2}= 0\) and \(W_{0} = I\), the GNNs model (1) reduce to the LFNNs model.

Before proceeding, recall the following lemmas which will be used throughout the proofs.

Lemma 1

([16])

For system (1), the following inequalities hold:

$$\begin{aligned}& 0\leqslant \int_{0}^{x_{i}(t)}\bigl(f_{i}(s)-k_{i}^{-}s \bigr) \,ds\leqslant \bigl[f_{i}\bigl(x_{i}(t) \bigr)-k_{i}^{-}x_{i}(t)\bigr]x_{i}(t), \\& 0\leqslant \int_{0}^{x_{i}(t)}\bigl(k_{i}^{+}s-f_{i}(s) \bigr) \,ds\leqslant \bigl[k_{i}^{+}x_{i}(t)-f_{i} \bigl(x_{i}(t)\bigr)\bigr]x_{i}(t). \end{aligned}$$

Lemma 2

(Wirtinger-based integral inequality [46])

For any matrix \(Z>0\), the following inequality holds for all continuously differentiable functions \(x: [\alpha, \beta] \rightarrow\mathbb{R}^{n}\):

$$ -(\beta-\alpha) \int_{\alpha}^{\beta}\dot{x}^{\mathrm{T}}(s)Z\dot {x}(s) \,ds\leq \varpi^{\mathrm{T}} \Omega\varpi, $$
(8)

where \(\varpi=[x^{\mathrm{T}}(\beta), x^{\mathrm{T}}(\alpha), \frac {1}{\beta-\alpha}\int_{\alpha}^{\beta}{x}^{\mathrm{T}}(s)\,ds]^{\mathrm {T}}\) and

$$\Omega=\left [ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} -4Z & -2Z & 6Z \\ * & -4Z & 6Z\\ * & * & -12Z \end{array}\displaystyle \right ]. $$

Remark 3

Corollary 9 in [51] has proofed that the Wirtinger-based integral inequality is equivalent to the free-matrix-based integral inequality proposed in [47]. However, the former involves a much smaller number of unknown variables to be determined than the latter. Therefore, the computational complexity of the application of a Wirtinger-based integral inequality combined with the reciprocally convex approach [44] is less than that of the free-matrix-based integral inequality [51]. In view of the above-mentioned facts, in this paper we adopt the Wirtinger-based integral inequality instead of the free-matrix-based integral inequality to handle the cross-product terms occurred in derivative of the constructed LKF for the sake of reducing the computational complexity.

Lemma 3

(Peng-Park’s integral inequality [45])

For any matrix \(\bigl [ {\scriptsize\begin{matrix}{} Z&S \cr *& Z\end{matrix}} \bigr ]\geq0\), positive scalars τ and \(\tau(t)\) satisfying \(0 < \tau(t)< \tau\), vector function \(\dot{x}:[-\tau,0]\rightarrow\mathbb{R}^{n}\) such that the concerned integrations are well defined, we have

$$-\tau \int_{t-\tau}^{t}\dot{x}^{\mathrm{T}}(s)Z\dot{x}(s)\,ds \leq\widetilde {\varpi}^{\mathrm{T}}(t) \widetilde{\Omega}\widetilde{\varpi}(t), $$

where \(\widetilde{\varpi}(t)=[x^{\mathrm{T}}(t),x^{\mathrm{T}}(t-\tau (t)),x^{\mathrm{T}}(t-\tau)]^{\mathrm{T}}\), and

$$\widetilde{\Omega}=\left [ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} -Z &Z-S&S \\ *& -2Z+\operatorname{He}(S)&Z-S \\ *&*&-Z \end{array}\displaystyle \right ]. $$

Lemma 4

([18, 52])

For any matrix \(Z \in\mathbb{R}^{n\times n}\), \(Z=Z^{\mathrm{T}}>0\), a scalar \(\tau>0\), and a vector-valued function \(\dot{x}: [-\tau,0]\rightarrow\mathbb{R}^{n}\) such that the following integrations are well defined, we have

$$ - \int_{-\tau}^{0} \int_{t+\theta}^{t}\dot{x}^{\mathrm{T}}(s)Z\dot {x}(s) \,ds \,d\theta\leq \widehat{\varpi}^{\mathrm{T}}(t) \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} -2Z & 2Z \\ * & -2Z \end{array}\displaystyle \right ]\widehat{\varpi}(t) , $$
(9)

where \(\widehat{\varpi}(t)=[x^{\mathrm{T}}(t), \frac{1}{\tau}\int _{t-\tau}^{t}{x}^{\mathrm{T}}(s)\,ds]^{\mathrm{T}}\).

Lemma 5

(Auxiliary function-based integral inequality [48])

Let x be a differentiable function: \([a,b] \rightarrow\mathbb{R}^{n}\). For a symmetric positive matrices \(R \in\mathbb{Z}^{n\times n}\), if the integrals concerned are well defined, then the following inequality holds:

$$ - \int_{a}^{b} \int_{\theta}^{b}\dot{x}^{\mathrm{T}}(s)Z\dot{x}(s)\,ds \,d\theta\leq \varpi^{\mathrm{T}}(a,b) \widehat{\Omega} \varpi(a,b), $$
(10)

where \(\varpi(a,b)=[x^{\mathrm{T}}(b), \frac{1}{b-a}\int _{a}^{b}{x}^{\mathrm{T}}(s)\,ds, \frac{1}{(b-a)^{2}}\int_{a}^{b}\int_{\theta }^{b}x^{\mathrm{T}}(s)\,ds \,d\theta]^{\mathrm{T}}\), and

$$\widehat{\Omega}=\left [ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} -6Z & -6Z & 24Z \\ * & -18Z & 48Z \\ * & * & -144Z \end{array}\displaystyle \right ]. $$

Lemma 6

(Finsler’s lemma [53])

Let \(\zeta\in\mathbb{R}^{n}\), \(\Phi=\Phi^{\mathrm{T}}\in\mathbb {R}^{n\times n}\), and \(B \in\mathbb{R}^{m\times n}\) such that \(\operatorname{rank}(B) < n\). Then the following statements are equivalent:

  1. (i)

    \(\zeta^{\mathrm{T}}\Phi\zeta<0\), \(\forall B\zeta=0\), \(\zeta\neq0\);

  2. (ii)

    \({B^{\perp}}^{\mathrm{T}}\Phi B^{\perp}<0\);

  3. (iii)

    \(\exists Y \in\mathbb{R}^{n\times m} \): \(\Phi+\operatorname{He}\{ YB\}<0\),

where \(B^{\perp}\in\mathbb{R}^{n\times(n-\operatorname{rank}(B))}\) is the right orthogonal complement of B.

3 Main results

By a delay-partitioning method, less conservative asymptotic stability criteria for GNN (1) are established in this section.

For any integer \(m\geq1\), define \(\delta=\frac{\tau}{m}\), then \([0,\tau]\) can be divided into m segments, i.e.,

$$ [0,\tau]=\bigcup_{i=1}^{m} \bigl[(i-1)\delta,i\delta\bigr]. $$
(11)

For any \(t\geq0\), there should exist an integer \(k \in\{1,\ldots,m\}\), such that \(\tau(t)\in[(k-1)\delta, k\delta]\).

For notational simplification, let

$$ \left \{ \textstyle\begin{array}{l} e_{s}= [\underbrace{0,\ldots,0}_{s - 1},I,\underbrace{0,\ldots ,0}_{2m-s+6} ]^{\mathrm{T}}, \quad s=1,2,\ldots,2m+6, \\ \zeta(t)= [x^{\mathrm{T}}(t-\tau(t)), \dot{x}^{\mathrm{T}}(t), f(W_{0}x(t)), f(W_{0}x(t -\tau(t))), \zeta_{1}^{\mathrm{T}}(t), x^{\mathrm {T}}(t-m\delta), \zeta_{2}^{\mathrm{T}}(t), \\ \hphantom{\zeta(t)={}}{}\frac{1}{\delta}\int_{t-m\delta}^{t-(m-1)\delta}x^{\mathrm{T}}(\theta )\,d\theta, \frac{1}{\delta^{2}}\int_{-\delta}^{0}\int_{t+\theta }^{t}x^{\mathrm{T}}(s)\,ds \,d\theta]^{\mathrm{T}}, \end{array}\displaystyle \right . $$
(12)

where \(\zeta_{1}(t)=[x^{\mathrm{T}}(t),x^{\mathrm{T}}(t-\delta),\ldots,x^{\mathrm {T}}(t-(m-1)\delta)]^{\mathrm{T}}\), \(\zeta_{2}(t)=[\frac{1}{\delta}\int_{t-\delta}^{t}x^{\mathrm{T}}(\theta )\,d\theta, \frac{1}{\delta}\int_{t-2\delta}^{t-\delta}x^{\mathrm {T}}(\theta)\,d\theta, \ldots, \frac{1}{\delta}\int_{t-(m-1)\delta }^{t-(m-2)\delta}x^{\mathrm{T}}(\theta)\,d\theta]^{\mathrm{T}}\).

Theorem 1

Given a positive integer m, scalars \(\tau \geq0\), \(\delta=\frac{\tau}{m}\), and μ, diagonal matrices \(K^{-}=\operatorname{diag}\{k_{1}^{-},k_{2}^{-},\ldots,k_{n}^{-}\}\), \(K^{+}=\operatorname{diag}\{ k_{1}^{+},k_{2}^{+},\ldots,k_{n}^{+}\}\), then GNN (1) with a time-varying delay \(\tau(t)\) satisfying (2) and (3) is asymptotically stable if there exist symmetric positive matrices \(P=[P_{ij}]_{(m+1)\times(m+1)}\in\mathbb{R}^{(m+1)n\times(m+1)n}\), \(Z_{0}, V_{0}, Z_{i}, Q_{i}, V_{i} \in\mathbb{R}^{n\times n}\) (\(i=1,\ldots,m\)), \(X_{i}\), \(\hat{X}_{j}\), \(R\in\mathbb{R}^{2n\times2n}\) (\(i=1,\ldots ,m-1\); \(j=1,\ldots,m-2\)), positive diagonal matrices \(\Lambda=\operatorname{diag}\{\lambda_{1},\ldots,\lambda_{n}\}\), \(\hat{\Lambda}=\operatorname{diag}\{\hat{\lambda}_{1},\ldots,\hat{\lambda}_{n}\}\), \(T, T_{l} \in\mathbb {R}^{n\times n}\) (\(l=1,\ldots,7\)), and any matrices \(Y\in\mathbb {R}^{(2m+6)n\times n}\) and \(S_{i}\in\mathbb{R}^{n\times n}\) (\(i=1,\ldots ,m\)), such that the following LMIs hold for \(k=1,\ldots,m\):

$$\begin{aligned}& \Psi(k)=\left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} Z_{k} & S_{k} \\ * & Z_{k} \end{array}\displaystyle \right ]\geq0, \quad i=1,\ldots,m, \end{aligned}$$
(13)
$$\begin{aligned}& \Theta(k)+\operatorname{He}\{Y\Gamma\}< 0, \end{aligned}$$
(14)

where

$$\begin{aligned}& \Gamma=-Ae_{5}^{\mathrm{T}}+W_{1}e_{3}^{\mathrm{T}}+W_{2}e_{4}^{\mathrm {T}}-e_{2}^{\mathrm{T}}, \\& \Theta(k) = \sum_{i=0, j\neq6,7}^{11} \Theta_{i} +\Theta_{6}(k)+\Theta _{7}(k)+e_{2} \Biggl(\delta^{2}\sum_{i=0}^{m}Z_{i}+ \frac{\delta^{2}}{2}\sum_{i=0}^{m}V_{i} \Biggr)e_{2}^{\mathrm{T}}, \\& \Theta_{0}= \left [ \textstyle\begin{array}{@{}c@{}} e_{5}^{\mathrm{T}} \\ e_{6}^{\mathrm{T}}\\ e_{m+6}^{\mathrm{T}} \end{array}\displaystyle \right ]^{\mathrm{T}} \Omega(0)\left [ \textstyle\begin{array}{@{}c@{}} e_{5}^{\mathrm{T}} \\ e_{6}^{\mathrm{T}}\\ e_{m+6}^{\mathrm{T}} \end{array}\displaystyle \right ]+\left [ \textstyle\begin{array}{@{}c@{}} e_{5}^{\mathrm{T}} \\ e_{m+6}^{\mathrm{T}}\\ e_{2m+6}^{\mathrm{T}} \end{array}\displaystyle \right ]^{\mathrm{T}} \widetilde{\Omega}(0)\left [ \textstyle\begin{array}{@{}c@{}} e_{5}^{\mathrm{T}} \\ e_{m+6}^{\mathrm{T}}\\ e_{2m+6}^{\mathrm{T}} \end{array}\displaystyle \right ], \\& \Theta_{1} = \operatorname{He} \left \{\left [ \textstyle\begin{array}{@{}c@{}} e_{5}^{\mathrm{T}} \\ \delta e_{m+6} ^{\mathrm{T}}\\ \vdots\\ \delta e_{2m+5} ^{\mathrm{T}} \end{array}\displaystyle \right ]^{\mathrm{T}} P \left [ \textstyle\begin{array}{@{}c@{}} e_{2} ^{\mathrm{T}}\\ e_{5}^{\mathrm{T}}-e_{6}^{\mathrm{T}} \\ \vdots\\ e_{m+4}^{\mathrm{T}}-e_{m+5}^{\mathrm{T}} \end{array}\displaystyle \right ] \right \}, \end{aligned}$$
$$\begin{aligned}& \Theta_{2}= \sum_{i=1}^{m-1}\left (\left [ \textstyle\begin{array}{@{}c@{}} e_{i+4}^{\mathrm{T}} \\ e_{i+5}^{\mathrm{T}} \end{array}\displaystyle \right ]^{\mathrm{T}}X_{i} \left [ \textstyle\begin{array}{@{}c@{}} e_{i+4}^{\mathrm{T}} \\ e_{i+5}^{\mathrm{T}} \end{array}\displaystyle \right ]-\left [ \textstyle\begin{array}{@{}c@{}} e_{i+5}^{\mathrm{T}} \\ e_{i+6}^{\mathrm{T}} \end{array}\displaystyle \right ]^{\mathrm{T}}X_{i}\left [ \textstyle\begin{array}{@{}c@{}} e_{i+5}^{\mathrm{T}} \\ e_{i+6}^{\mathrm{T}} \end{array}\displaystyle \right ] \right ) \\& \hphantom{\Theta_{2}={}}{}+\sum_{i=1}^{m-2}\left (\left [ \textstyle\begin{array}{@{}c@{}} e_{m+i+5}^{\mathrm{T}} \\ e_{m+i+6}^{\mathrm{T}} \end{array}\displaystyle \right ]^{\mathrm{T}}\hat{X}_{i}\left [ \textstyle\begin{array}{@{}c@{}} e_{m+i+5}^{\mathrm{T}} \\ e_{m+i+6}^{\mathrm{T}} \end{array}\displaystyle \right ]-\left [ \textstyle\begin{array}{@{}c@{}} e_{m+i+6}^{\mathrm{T}} \\ e_{m+i+7}^{\mathrm{T}} \end{array}\displaystyle \right ]^{\mathrm{T}}\hat{X}_{i} \left [ \textstyle\begin{array}{@{}c@{}} e_{m+i+6}^{\mathrm{T}} \\ e_{m+i+7}^{\mathrm{T}} \end{array}\displaystyle \right ] \right ), \\& \Theta_{3}=\operatorname{He} \bigl\{ \bigl[\bigl(e_{3}-e_{5}W_{0}^{\mathrm{T}}{K^{-}} \bigr)\Lambda +\bigl(e_{5}W_{0}^{\mathrm{T}}{K^{+}}-e_{3} \bigr)\Lambda'\bigr]W_{0}e^{\mathrm{T}}_{2} \bigr\} , \\& \Theta_{4}= \begin{bmatrix} e_{5}^{\mathrm{T}} \\ e_{3}^{\mathrm{T}} \end{bmatrix} ^{\mathrm{T}} R \begin{bmatrix} e_{5}^{\mathrm{T}} \\ e_{3}^{\mathrm{T}} \end{bmatrix} -(1-\mu) \begin{bmatrix} e_{1}^{\mathrm{T}} \\ e_{4}^{\mathrm{T}} \end{bmatrix} ^{\mathrm{T}} R \begin{bmatrix} e_{1}^{\mathrm{T}} \\ e_{4}^{\mathrm{T}} \end{bmatrix} , \\& \Theta_{5}=\bigl(e_{5}W_{0}^{\mathrm{T}} K T K W_{0} e_{5}^{\mathrm{T}}-e_{3} T e_{3}^{\mathrm{T}}\bigr) -(1-\mu) \bigl(e_{1}W_{0}^{\mathrm{T}} K T K W_{0}e_{1}^{\mathrm {T}}-e_{4} T e_{4}^{\mathrm{T}}\bigr), \\& \Theta_{6}(k)= \sum_{i=1}^{k-1} \bigl[e_{i+4}Q_{i}e_{i+4}^{\mathrm{T}}- e_{i+5}Q_{i}e_{i+5}^{\mathrm{T}} \bigr] +e_{k+4}Q_{k}e_{k+4}^{\mathrm{T}}- (1- \mu)e_{1}Q_{k}e^{\mathrm{T}}_{1}, \\& \Theta_{7}(k)= \sum_{i=1,i\neq k}^{m} \left [ \textstyle\begin{array}{@{}c@{}} e_{i+4}^{\mathrm{T}} \\ e_{i+5}^{\mathrm{T}} \\ e_{m+i+5}^{\mathrm{T}} \end{array}\displaystyle \right ]^{\mathrm{T}}\Omega(i) \left [ \textstyle\begin{array}{@{}c@{}} e_{i+4}^{\mathrm{T}} \\ e_{i+5}^{\mathrm{T}} \\ e_{m+i+5}^{\mathrm{T}} \end{array}\displaystyle \right ] + \left [ \textstyle\begin{array}{@{}c@{}} e_{k+4}^{\mathrm{T}} \\ e_{1}^{\mathrm{T}}\\ e_{k+5}^{\mathrm{T}} \end{array}\displaystyle \right ]^{\mathrm{T}} \widehat{\Omega}(k) \left [ \textstyle\begin{array}{@{}c@{}} e_{k+4}^{\mathrm{T}} \\ e_{1}^{\mathrm{T}}\\ e_{k+5}^{\mathrm{T}} \end{array}\displaystyle \right ], \\& \Theta_{8}= \sum_{i=1}^{m} \left [ \textstyle\begin{array}{@{}c@{}} e_{i+4}^{\mathrm{T}} \\ e_{m+i+5}^{\mathrm{T}} \end{array}\displaystyle \right ]^{\mathrm{T}} \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} -2V_{i} & 2V_{i} \\ * & -2V_{i} \end{array}\displaystyle \right ] \left [ \textstyle\begin{array}{@{}c@{}} e_{i+4}^{\mathrm{T}} \\ e_{m+i+5}^{\mathrm{T}} \end{array}\displaystyle \right ], \\& \Theta_{9}=\operatorname{He} \bigl\{ \bigl(e_{3}-e_{5}W_{0}^{\mathrm {T}}K^{-} \bigr)T_{1}\bigl(K^{+}W_{0}e_{5}^{\mathrm{T}}-e_{3}^{\mathrm {T}} \bigr)+\bigl(e_{4}-e_{1}W_{0}^{\mathrm{T}}K^{-} \bigr)T_{2}\bigl(K^{+}W_{0}e_{1}^{\mathrm {T}}-e_{4}^{\mathrm{T}} \bigr) \bigr\} , \\& \Theta_{10}=\operatorname{He} \bigl\{ \bigl[(e_{3}-e_{4})-(e_{5}-e_{1})W_{0}^{\mathrm {T}}K^{-} \bigr]T_{3} \bigl[K^{+}W_{0}\bigl(e_{5}^{\mathrm{T}}-e_{1}^{\mathrm{T}} \bigr)-\bigl(e_{3}^{\mathrm {T}}-e_{4}^{\mathrm{T}}\bigr) \bigr] \bigr\} , \\& \Theta_{11}=\operatorname{He}\bigl\{ \bigl[\bigl(e_{5}W_{0}^{\mathrm{T}} {K^{+}} -e_{3}\bigr)T_{4}+ \bigl(e_{3}-e_{5}W_{0}^{\mathrm{T}}K^{-} \bigr)T_{5}\bigr]W_{0}e_{5}^{\mathrm{T}} \\& \hphantom{\Theta_{11}={}}{}+\bigl[\bigl(e_{1}W_{0}^{\mathrm{T}} {K^{+}}-e_{4}\bigr)T_{6}+\bigl(e_{4}-e_{1}W_{0}^{\mathrm{T}} K^{-}\bigr)T_{7}\bigr]W_{0}e_{1}^{\mathrm{T}} \bigr\} , \end{aligned}$$

with

$$\begin{aligned}& \widehat{\Omega}(k)=\left [ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} -Z_{k} & Z_{k}-S_{k} & S_{k} \\ * & -2Z_{k}+\operatorname{He}(S_{k}) & Z_{k}-S_{k} \\ * & * & -Z_{k} \end{array}\displaystyle \right ], \\& \widetilde{\Omega}(0)= \left [ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} -6V_{0} & -6V_{0} & 24V_{0} \\ * & -18V_{0} & 48V_{0}\\ * & * & -144V_{0} \end{array}\displaystyle \right ], \\& \Omega(i)= \left [ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} -4Z_{i} & -2Z_{i} & 6Z_{i} \\ * & -4Z_{i} & 6Z_{i}\\ * & * & -12Z_{i} \end{array}\displaystyle \right ] \quad (i=0,1, \ldots,m, i\neq k). \end{aligned}$$

Proof

For any \(t\geq0\), there should exist an integer \(k \in \{1,\ldots,m\}\), such that \(\tau(t)\in[(k-1)\delta, k\delta]\). Then, according to (5) and Lemma 1, choose the following LKF candidate:

$$ V(t,x_{t})|_{\{\tau(t)\in[(k-1)\delta, k\delta]\}} =\sum _{i = 1}^{8} V_{i}(x_{t}) , $$
(15)

where

$$\begin{aligned}& V_{1}(x_{t})=\eta^{\mathrm{T}}(t) P\eta(t), \\& V_{2}(x_{t})=\sum_{i=1}^{m-1} \int_{t-\delta}^{t} \eta_{i}^{\mathrm {T}}(s)X_{i} \eta_{i}(s)\,ds+\sum_{i=1}^{m-2} \int_{t-\delta}^{t} \hat{\eta }_{i}^{\mathrm{T}}(s) \hat{X}_{i}\hat{\eta}_{i}(s)\,ds, \\& V_{3}(x_{t})=2\sum_{i = 1}^{n} \int_{0}^{W_{0i}x(t)} \bigl[\lambda_{i} \bigl(f_{i} (s) - k_{i}^{-} s\bigr) + \lambda'_{i} \bigl(k _{i}^{+} s - f_{i} (s)\bigr) \bigr] \,ds, \\& V_{4} (x_{t}) = \int_{t - \tau(t)}^{t} \begin{bmatrix} {x(s)} \\ {f(W_{0}x(s)) } \end{bmatrix} ^{\mathrm{T}} R \begin{bmatrix} {x(s)} \\ {f(W_{0}x(s)) } \end{bmatrix} \,ds, \\& V_{5} (x_{t}) = \int_{t - \tau(t)}^{t} \bigl[x^{\mathrm{T}}(s)W_{0}^{\mathrm{T}} K T K W_{0} x(s)-f^{\mathrm{T}}\bigl(W_{0} x(s)\bigr) T f \bigl(W_{0} x(s)\bigr)\bigr] \,ds, \\& V_{6}(x_{t})=\sum_{i=1}^{k-1} \int_{t-i\delta}^{t-(i-1)\delta} x^{\mathrm {T}}(s)Q_{i}x(s) \,ds+ \int_{t-\tau(t)}^{t-(k-1)\delta} x^{\mathrm{T}}(s)Q_{k}x(s) \,ds, \\& V_{7}(x_{t})=\sum_{i=1}^{m} \delta \int_{-i\delta}^{-(i-1)\delta} \int _{t+\theta}^{t} \dot{x}^{\mathrm{T}}(s)Z_{i} \dot{x}(s)\,ds\,d\theta+ \delta \int_{-\delta}^{0} \int_{t+\theta}^{t} \dot{x}^{\mathrm{T}}(s)Z_{0} \dot {x}(s)\,ds\,d\theta, \\& V_{8}(x_{t})=\sum_{i=1}^{m} \int_{-i\delta}^{-(i-1)\delta} \int_{\theta }^{-(i-1)\delta} \int_{t+\alpha}^{t} \dot{x}^{\mathrm{T}}(s)V_{i} \dot {x}(s)\, ds\, d \alpha \,d\theta \\& \hphantom{V_{8}(x_{t})={}}{}+ \int_{-\delta}^{0} \int_{\theta}^{0} \int _{t+\alpha}^{t} \dot{x}^{\mathrm{T}}(s)V_{0} \dot{x}(s)\,ds\,d \alpha \,d\theta, \end{aligned}$$

with \(\eta(t)=[x^{\mathrm{T}}(t),\delta\zeta^{\mathrm{T}}_{2}(t), \int _{t-m\delta}^{t-(m-1)\delta}x^{\mathrm{T}}(\theta)\,d\theta]^{\mathrm {T}}\), \(\eta_{i}(s)=[x^{\mathrm{T}}(s-(i-1)\delta),x^{\mathrm{T}}(s-i\delta )]^{\mathrm{T}}\), \(\hat{\eta}_{i}(s)=[\frac{1}{\delta}\int_{s-i\delta }^{s-(i-1)\delta}x^{\mathrm{T}}(\theta)\,d\theta, \frac{1}{\delta}\int _{s-(i+1)\delta}^{s-i\delta}x^{\mathrm{T}}(\theta)\,d\theta]^{\mathrm {T}}\) and \(W_{0i}\) being the ith row vector of the matrix \(W_{0}\).

Taking the derivative of \(V(x_{t})\) along the solution of GNN (1) yields

$$ \dot{V}(x_{t})|_{\{\tau(t)\in[(k-1)\delta, k\delta]\}} = \sum _{i=1}^{8}\dot{V}_{i}(x_{t}), $$
(16)

where

$$\begin{aligned}& \dot{V}_{1}(x_{t}) =2\eta^{\mathrm{T}}(t) P \dot{\eta}(t)= \zeta^{\mathrm {T}}(t)\Theta_{1}\zeta(t), \end{aligned}$$
(17)
$$\begin{aligned}& \dot{V}_{2}(x_{t})=\sum_{i=1}^{m-1} \bigl[\eta_{i}^{\mathrm{T}}(t)X_{i}\eta_{i}(t)- \eta_{i}^{\mathrm{T}}(t-\delta) X_{i}\eta_{i}(t- \delta)\bigr] \\& \hphantom{\dot{V}_{2}(x_{t})={}}{}+\sum_{i=1}^{m-2} \bigl[\hat{ \eta}_{i}^{\mathrm{T}}(t)\hat{X}_{i}{\hat{\eta}}_{i}(t)-{\hat{\eta}}_{i}^{\mathrm{T}}(t-\delta)\hat{X}_{i}\hat{\eta}_{i}(t-\delta)\bigr] \\& \hphantom{\dot{V}_{2}(x_{t})}= \zeta^{\mathrm{T}}(t)\Theta_{2}\zeta(t), \end{aligned}$$
(18)
$$\begin{aligned}& \dot{V}_{3}(x_{t})=2\bigl\{ \bigl[f \bigl(W_{0}x(t)\bigr)-K^{-}W_{0}x(t)\bigr]^{\mathrm{T}}\Lambda + \bigl[K^{+}W_{0}x(t)-f\bigl(W_{0}x(t)\bigr) \bigr]^{\mathrm{T}}\Lambda'\bigr\} W_{0} \dot{x}(t) \\& \hphantom{\dot{V}_{3}(x_{t})}= \zeta ^{\mathrm{T}}(t)\Theta_{3}\zeta(t), \end{aligned}$$
(19)
$$\begin{aligned}& \dot{V}_{4}(x_{t}) \leqslant \begin{bmatrix} {x(t)} \\ {f(W_{0}x(t)) } \end{bmatrix} ^{\mathrm{T}} R \begin{bmatrix} {x(t)} \\ {f(W_{0}x(t)) } \end{bmatrix} \\& \hphantom{\dot{V}_{4}(x_{t}) \leqslant{}}{}-(1-\mu) \begin{bmatrix} {x(t-\tau(t))} \\ {f(W_{0}x(t-\tau(t))) } \end{bmatrix} ^{\mathrm{T}} R \begin{bmatrix} {x(t-\tau(t))} \\ {f(W_{0}x(t-\tau(t))) } \end{bmatrix} \\& \hphantom{\dot{V}_{4}(x_{t})}= \zeta^{\mathrm{T}}(t)\Theta_{4} \zeta(t), \end{aligned}$$
(20)
$$\begin{aligned}& \dot{V}_{5}(x_{t}) \leqslant \bigl[x^{\mathrm{T}}(t)W_{0}^{\mathrm{T}} K T K W_{0} x(t)-f^{\mathrm{T}}\bigl(W_{0} x(t)\bigr)Tf \bigl(W_{0} x(t)\bigr)\bigr] \\& \hphantom{\dot{V}_{5}(x_{t}) \leqslant{}}{}-(1-\mu) \bigl[x^{\mathrm{T}}\bigl(t-\tau(t) \bigr)W_{0}^{\mathrm{T}} K T K W_{0} x\bigl(t-\tau (t) \bigr) \\& \hphantom{\dot{V}_{5}(x_{t}) \leqslant{}}{}-f^{\mathrm{T}}\bigl(W_{0} x\bigl(t-\tau(t)\bigr)\bigr)Tf \bigl(W_{0} x\bigl(t-\tau(t)\bigr)\bigr)\bigr] \\& \hphantom{\dot{V}_{5}(x_{t})}= \zeta^{\mathrm{T}}(t)\Theta_{5} \zeta(t), \end{aligned}$$
(21)
$$\begin{aligned}& \dot{V}_{6}(x_{t})\leqslant\sum _{i=1}^{k-1} \bigl[x^{\mathrm{T}}\bigl(t-(i-1)\delta \bigr)Q_{i}x\bigl(t-(i-1)\delta\bigr) -x^{\mathrm {T}}(t-i \delta)Q_{i}x(t-i\delta)\bigr] \\& \hphantom{\dot{V}_{6}(x_{t})\leqslant{}}{}+x^{\mathrm{T}}\bigl(t-(k-1)\delta\bigr)Q_{k}x \bigl(t-(k-1)\delta\bigr) -(1-\mu)x^{\mathrm {T}}\bigl(t-\tau(t) \bigr)Q_{k}x\bigl(t-\tau(t)\bigr) \\& \hphantom{\dot{V}_{6}(x_{t})}= \zeta^{\mathrm{T}}(t)\Theta_{6}(k) \zeta(t), \end{aligned}$$
(22)
$$\begin{aligned}& \dot{V}_{7}(x_{t}) =\dot{x}^{\mathrm{T}}(t) \Biggl(\delta^{2}\sum_{i=0}^{m}Z_{i} \Biggr)\dot{x}(t)-\delta\sum_{i=1}^{m} \int_{t-i\delta }^{t-(i-1)\delta}\dot{x}^{\mathrm{T}}(s)Z_{i} \dot{x}(s)\,ds \\& \hphantom{\dot{V}_{7}(x_{t}) ={}}{}-\delta \int _{t-\delta}^{t}\dot{x}^{\mathrm{T}}(s)Z_{0} \dot{x}(s)\,ds, \end{aligned}$$
(23)
$$\begin{aligned}& \dot{V}_{8}(x_{t}) = \dot{x}^{\mathrm{T}}(t) \Biggl(\frac{\delta^{2}}{2}\sum_{i=0}^{m}V_{i} \Biggr)\dot{x}(t) -\sum_{i=1}^{m} \int_{-i\delta}^{-(i-1)\delta} \int_{t+\theta }^{t-(i-1)\delta} \dot{x}^{\mathrm{T}}(s)V_{i} \dot{x}(s)\,ds\,d\theta \\& \hphantom{\dot{V}_{8}(x_{t}) ={}}{}- \int_{-\delta}^{0} \int_{t+\theta}^{t} \dot{x}^{\mathrm{T}}(s)V_{0} \dot {x}(s)\,ds\,d\theta. \end{aligned}$$
(24)

Applying Lemma 2 and Lemma 3 to bound the second item in (23), then it follows from (13) that

$$\begin{aligned}& -\delta\sum_{i=1}^{m} \int_{t-i\delta}^{t-(i-1)\delta}\dot{x}^{\mathrm {T}}(s)Z_{i} \dot{x}(s)\,ds \\& \quad \leq\sum_{i=1,i\neq k}^{m} \varpi^{\mathrm {T}}_{1}(i,t) \Omega(i) \varpi_{1}(i,t)+ \varpi_{2}^{\mathrm{T}}(k,t)\widehat{\Omega}(k) \varpi_{2}(k,t) =\zeta^{\mathrm{T}}(t)\Theta_{7}(k)\zeta(t), \end{aligned}$$
(25)

where \(\varpi_{1}(i,t)= [ x^{\mathrm{T}}(t-(i-1)\delta), x^{\mathrm {T}}(t-i\delta), \frac{1}{\delta}\int_{t-i\delta}^{t-(i-1)\delta }x^{\mathrm{T}}(s)\,ds ]^{\mathrm{T}}\), \(\varpi_{2}(k,t)= [x^{\mathrm {T}}(t-(k-1)\delta),x^{\mathrm{T}}(t-\tau(t)),x^{\mathrm{T}}(t-k\delta )]^{\mathrm{T}}\), and \(\Omega(i)\), \(\widehat{\Omega}(k)\) are defined in Theorem 1.

Using Lemma 4 to estimate the integral item \(-\sum_{i=1}^{m}\int _{-i\delta}^{-(i-1)\delta}\int_{t+\theta}^{t-(i-1)\delta} \dot {x}^{\mathrm{T}}(s)V_{i}\dot{x}(s)\,ds\,d\theta\) in (24) yields

$$\begin{aligned}& -\sum_{i=1}^{m} \int_{-i\delta}^{-(i-1)\delta} \int_{t+\theta }^{t-(i-1)\delta} \dot{x}^{\mathrm{T}}(s)V_{i} \dot{x}(s)\,ds\,d\theta \\& \quad \leq\sum_{i=1}^{m} \varpi^{\mathrm{T}}_{3}(i,t) \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} -2V_{i} & 2V_{i} \\ * & -2V_{i} \end{array}\displaystyle \right ] \varpi_{3}(i,t) =\zeta^{\mathrm{T}}(t) \Theta_{8}\zeta(t), \end{aligned}$$
(26)

where \(\varpi_{3}(i,t)= [x^{\mathrm{T}}(t-(i-1)\delta),\frac {1}{\delta}\int_{t-i\delta}^{t-(i-1)\delta}x^{\mathrm{T}}(\theta)\,d\theta ]^{\mathrm{T}}\) and \(\Theta_{8}\) is defined in Theorem 1.

On the other hand, it follows from Lemma 2 and Lemma 5 that

$$\begin{aligned}& -\delta \int_{t-\delta}^{t}\dot{x}^{\mathrm{T}}(s)Z_{0} \dot{x}(s)\,ds- \int _{-\delta}^{0} \int_{t+\theta}^{t} \dot{x}^{\mathrm{T}}(s)V_{0} \dot {x}(s)\,ds\,d\theta \\& \quad \leq\varpi_{4} ^{\mathrm{T}}(t) \Omega(0) \varpi_{4} (t)+\varpi_{5} ^{\mathrm{T}}(t) \widetilde{ \Omega}(0) \varpi_{5} (t)=\zeta^{\mathrm{T}}(t)\Theta_{0} \zeta(t), \end{aligned}$$
(27)

where \(\varpi_{4}(t)= [x^{\mathrm{T}}(t),x^{\mathrm{T}}(t-\delta),\frac {1}{\delta}\int_{t-\delta}^{t}x^{\mathrm{T}}(s)\,ds ]^{\mathrm{T}}\), \(\varpi_{5}(t)= [x^{\mathrm{T}}(t),\frac{1}{\delta}\int_{t-\delta }^{t}x^{\mathrm{T}}(s)\,ds, \frac{1}{\delta^{2}}\int_{-\delta}^{0}\int _{t+\theta}^{t}x^{\mathrm{T}}(s)\,ds \,d\theta ]^{\mathrm{T}}\), and \(\Omega(0)\), \(\widetilde{\Omega}(0)\) and \(\Theta_{0}\) are defined in Theorem 1.

In addition, for positive diagonal matrices \(T_{l}\) (\(l=1,\ldots,7\)) with appropriate dimensions, the following inequalities hold from (6), (7), and Lemma 1:

$$\begin{aligned}& 0\leq2\bigl[f^{\mathrm{T}} \bigl(W_{0}x(t)\bigr)-x^{\mathrm{T}}(t)W_{0}^{\mathrm {T}}K^{-} \bigr]T_{1}\bigl[K^{+}W_{0}x(t)-f \bigl(W_{0}x(t) \bigr)\bigr] \\& \hphantom{0\leq{}}{}+2\bigl[f^{\mathrm{T}} \bigl(W_{0}x\bigl(t-\tau(t) \bigr)\bigr)-x^{\mathrm{T}}\bigl(t-\tau (t)\bigr)W_{0}^{\mathrm{T}}K^{-} \bigr] \\& \hphantom{0\leq{}}{}\times T_{2}\bigl[K^{+}W_{0}x\bigl(t-\tau(t)\bigr)-f \bigl(W_{0}x\bigl(t-\tau(t)\bigr)\bigr)\bigr], \\& 0\leq2\bigl[\bigl(f^{\mathrm{T}} \bigl(W_{0}x(t)\bigr)-f^{\mathrm{T}} \bigl(W_{0}x\bigl(t-\tau (t)\bigr)\bigr)\bigr)-\bigl(x^{\mathrm{T}}(t)-x^{\mathrm{T}} \bigl(t-\tau(t)\bigr)\bigr)W_{0}^{\mathrm{T}}K^{-}\bigr]T_{3} \\& \hphantom{0\leq{}}{}\times\bigl[K^{+}W_{0}\bigl(x(t)-x\bigl(t-\tau(t)\bigr) \bigr)-\bigl(f \bigl(W_{0}x(t)\bigr)-f\bigl(W_{0}x\bigl(t- \tau(t)\bigr)\bigr)\bigr)\bigr], \\& 0\leq2 \bigl\{ \bigl[K^{+}W_{0}x(t)-f\bigl(W_{0}x(t) \bigr)\bigr]^{\mathrm{T}} T_{4} + \bigl[f\bigl(W_{0}x(t) \bigr)-K^{-}W_{0}x(t)\bigr]^{\mathrm{T}}T_{5} \bigr\} W_{0}x(t) \\& \hphantom{0\leq{}}{}+2 \bigl\{ \bigl[K^{+}W_{0}x\bigl(t-\tau(t) \bigr)-f\bigl(W_{0}x\bigl(t-\tau(t)\bigr)\bigr)\bigr]^{\mathrm{T}}T_{6} \\& \hphantom{0\leq{}}{}+\bigl[f\bigl(W_{0}x\bigl(t-\tau(t)\bigr)\bigr)-K^{-}W_{0}x \bigl(t-\tau(t)\bigr)\bigr]^{\mathrm{T}}T_{7} \bigr\} W_{0}x\bigl(t-\tau(t)\bigr), \end{aligned}$$

which imply

$$ \zeta^{\mathrm{T}}(t)[\Theta_{9}+\Theta_{10}+ \Theta_{11}]\zeta (t)\geqslant 0, $$
(28)

where \(\Theta_{9}\), \(\Theta_{10}\), and \(\Theta_{11}\) are defined in Theorem 1.

Then, by (16)-(28), and the S-procedure, the following inequality holds:

$$ \dot{V}(t,x_{t})|_{\{\tau(t)\in[(k-1)\delta, k\delta]\}} \leq \zeta ^{\mathrm{T}}(t)\Theta(k)\zeta(t), $$
(29)

where \(\Theta(k)\) is defined in Theorem 1.

In the following, GNN (1) with the augmented vector \(\zeta (t)\) can be rewritten as

$$ 0 = \Gamma\zeta(t), $$

where Γ is defined in Theorem 1.

Therefore, the asymptotic stability conditions for GNN (1) can be represented by

$$\begin{aligned}& \quad\quad\quad~\zeta^{\mathrm{T}}(t)\Theta(k)\zeta(t)< 0, \\& \quad \textit{subject to}~~~0 = \Gamma \zeta(t). \end{aligned}$$
(30)

By Finsler’s lemma, for \(Y\in\mathbb{R}^{(2m+6)n\times n}\), (30) is equivalent to

$$ \zeta^{\mathrm{T}}(t)\bigl[\Theta(k)+\operatorname{He} \{Y \Gamma \}\bigr]\zeta (t)< 0. $$
(31)

Then, it follows from (29), (30), (31), and LMIs (14) that \(\dot{V}(t,x_{t})|_{\{\tau(t)\in[(k-1)\delta , k\delta]\}}<0\), i.e., \(\dot{V}(t,x_{t})|_{\{\tau(t)\in[(k-1)\delta, k\delta]\}}<-\gamma \Vert x(t)\Vert ^{2} \) for a sufficiently small \(\gamma>0\). Therefore, by the Lyapunov-Krasovskii stability theorem [7], GNN (1) with any delay \(\tau(t)\) satisfying (2) and (3) is globally asymptotically stable. This completes the proof. □

Remark 4

For stability analysis for GNN (1), the modified augmented LKF (15) is quite different from those in [1–5] in the following respects: (a) the augmented LKF with more information as regards the activation functions is established by partitioning the delay in integral terms. And the delay-partitioning-dependent triple integral term \(\sum_{i=1}^{m}\int_{-i\delta}^{-(i-1)\delta}\int_{\theta}^{-(i-1)\delta}\int _{t+\alpha}^{t} \dot{x}^{\mathrm{T}}(s)V_{i}\dot{x}(s)\,ds\,d \alpha \,d\theta\) is also introduced in the LKF; (b) the \([P_{ij}]_{(m+1)\times(m+1)}\)-dependent sub-LKF is included, so the relationships between the augmented state vectors \([x^{\mathrm {T}}(t),x^{\mathrm{T}}(t-\delta),\ldots,x^{\mathrm{T}}(t-m\delta )]^{\mathrm{T}}\) and \([\frac{1}{\delta}\int_{t-\delta}^{t}x^{\mathrm {T}}(s)\,ds,\frac{1}{\delta}\int_{t-2\delta}^{t-\delta}x^{\mathrm {T}}(s)\,ds, \ldots, \frac{1}{\delta}\int_{t-m\delta}^{t-(m-1)\delta }x^{\mathrm{T}}(s)\,ds]^{\mathrm{T}}\) have been fully taken into account. With these differences and advantages, less conservative results than those in [1–5] can be expected, which will be demonstrated later by two numerical examples.

Remark 5

New tighter bounding inequalities such as the Wirtinger-based integral inequality, Peng-Park’s integral inequality, and an auxiliary function-based integral inequality have been, respectively, employed to handle the integral terms \(-\delta \sum_{i=1,i\neq k}^{m} \int_{t-i\delta}^{t-(i-1)\delta} \dot{x}^{\mathrm {T}}(s) Z_{i}\dot{x}(s)\,ds\), \(-\delta\int_{t-k\delta}^{t-(k-1)\delta}\dot {x}^{\mathrm{T}}(s)Z_{k}\dot{x}(s)\,ds\), and \(-\int_{-\delta}^{0}\int _{t+\theta}^{t} \dot{x}^{\mathrm{T}}(s)V_{0}\dot{x}(s)\,ds\,d\theta\), which can reduce the enlargement in bounding the derivative of the LKF. Therefore, less conservative results than existing ones [1–5, 13–15, 17–20, 22, 23, 25, 26, 29] can be achieved. This will be verified by numerical examples later.

Finally, in the case of the time-varying delay \(\tau(t)\) being non-differentiable or unknown \(\dot{\tau}(t)\), the following corollary is readily obtained by setting \(R=T=0\) and \(Q_{k}=0\) (\(Q_{j}\neq0\), \(j=1,\ldots,k-1\)) in Theorem 1.

Corollary 1

Given a positive integer m, scalars \(\tau \geq0\), and \(\delta=\frac{\tau}{m}\), diagonal matrices \(K^{-}=\operatorname{diag}\{k_{1}^{-},k_{2}^{-},\ldots,k_{n}^{-}\}\), \(K^{+}=\operatorname{diag}\{ k_{1}^{+},k_{2}^{+},\ldots,k_{n}^{+}\}\), then GNN (1) with a time-varying delay \(\tau(t)\) satisfying (2) is asymptotically stable if there exist symmetric positive matrices \(P=[P_{ij}]_{(m+1)\times (m+1)}\in\mathbb{R}^{(m+1)n\times(m+1)n}\), \(Z_{0}, V_{0}, Z_{i}, Q_{i}, V_{i} \in \mathbb{R}^{n\times n}\) (\(i=1,\ldots,m\)), \(X_{i}, \hat{X}_{j} \in\mathbb{R}^{2n\times2n}\) (\(i=1,\ldots,m-1\); \(j=1,\ldots ,m-2\)), positive diagonal matrices \(T_{l} \in\mathbb{R}^{n\times n}\) (\(l=1,\ldots,3\)), \(\Lambda=\operatorname{diag}\{\lambda_{1},\ldots,\lambda_{n}\}\), \(\hat{\Lambda}=\operatorname{diag}\{\hat{\lambda}_{1},\ldots,\hat{\lambda}_{n}\}\), and any matrices \(Y\in \mathbb{R}^{(2m+5)n\times n}\) and \(S_{i}\in\mathbb{R}^{n\times n}\) (\(i=1,\ldots,m\)), such that the following LMIs hold for \(k=1,\ldots,m\):

$$\begin{aligned}& \Psi(k) \geq0, \end{aligned}$$
(32)
$$\begin{aligned}& \widetilde{\Theta}(k)+\operatorname{He}\{Y\Gamma\}< 0, \end{aligned}$$
(33)

where

$$\widetilde{\Theta}(k)= \sum_{i=0,i\neq4,\ldots,7}^{11} \Theta_{i} +\widetilde{\Theta}_{6}(k)+ \Theta_{7}(k) +e_{2} \Biggl(\delta^{2}\sum_{i=0}^{m}Z_{i}+ \frac{\delta^{2}}{2}\sum_{i=0}^{m}V_{i} \Biggr)e_{2}^{\mathrm{T}}, $$

with \(\widetilde{\Theta}_{6}(k)= \sum_{i=1}^{k-1} [e_{i+4}Q_{i}e_{i+4}^{\mathrm{T}}- e_{i+5}Q_{i}e_{i+5}^{\mathrm{T}} ]\), and \(\Psi(k)\), Y, Γ, \(\Theta_{i}\), and \(\Theta_{7}(k)\) are, respectively, defined in Theorem  1.

4 Numerical examples

In this section, two examples are introduced to illustrate the merits of the derived results.

Example 1

Consider the delayed GNN (1) subject to (4) with the following parameters:

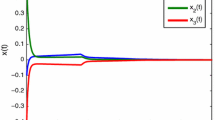
$$\begin{aligned}& W_{0} = I,\qquad K^{-} = 0,\qquad K^{+} =\operatorname{diag}\{0.1137, 0.1279, 0.7994, 0.2368\}, \\& A =\operatorname{diag}\{1.2769, 0.6231, 0.9230, 0.4480\}, \\& W_{1}=\left [ { \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{}} -0.0373& 0.4852& -0.3351& 0.2336\\ -1.6033 &0.5988 &-0.3224& 1.2352\\ 0.3394 &-0.0860 &-0.3824 &-0.5785\\ -0.1311& 0.3253 &-0.9534 &-0.5015 \end{array}\displaystyle } \right ], \\& W_{2} = \left [ { \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{}} 0.8674& -1.2405& -0.5325& 0.0220\\ 0.0474 & -0.9164& 0.0360 & 0.9816\\ 1.8495& 2.6117& -0.3788& 0.8428\\ -2.0413 & 0.5179& 1.1734 & -0.2775 \end{array}\displaystyle } \right ]. \end{aligned}$$

As a delayed LFNN, the above-mentioned example has been widely studied in [1, 2, 4, 5, 13, 14, 17, 18, 20, 22, 25, 26, 29]. For comparison, the MAUBs (maximum admissible upper bounds) of \(\tau (t)\) derived from Theorem 1 and Corollary 1 with various values of μ and m are summarized in Table 1. As shown in this table, the stability criterion derived in this paper has been improved by comparing with previous ones [1, 2, 4, 5, 13, 17, 20, 22, 25, 26, 29]. For the initial state condition \([-1,0.3,-0.4,1]^{\mathrm{T}}\), \(\mu=0.5\), and \(\tau=3.92\), Figure 1 depicts the state trajectories of the given LFNNs with activation functions \(f_{1}(s)=0.0568(|s+1|-|s-1|)\), \(f_{2}(s)=0.0640(|s+1|-|s-1|)\), \(f_{3}(s)=0.3997(|s+1|-|s-1|)\), \(f_{4}(s)=0.1184(|s+1|-|s-1|) \) and time-varying delay \(\tau (t)=1.96(1-\sin(0.254t))\). Figure 1 shows that the MAUBs listed in Table 2 are capable of guaranteeing asymptotical stability of the considered LFNNs with the given parameters.

Figure 1
figure 1

The state responses of the given LFNNs in Example 1 .

Full size image
Table 1 The achieved MAUBs of \(\pmb{\tau(t)}\) for various values of μ - Example 1
Full size table
Table 2 The achieved MAUBs of \(\pmb{\tau(t)}\) for various values of μ - Example 2
Full size table

Example 2

Consider the delayed GNN (1) subject to (4) with the following parameters:

$$\begin{aligned}& W_{1} = 0, \qquad W_{2} = I,\qquad K^{-} = 0, \\& K^{+} = \operatorname{diag}\{0.3680, 0.1795, 0.2876\},\qquad A =\operatorname{diag} \{7.3458, 6.9987, 5.5949\}, \\& W_{0}=\left [ { \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} 13.6014& -2.9616& -0.6936\\ 7.4736 &21.6810& 3.2100\\ 0.7920 &-2.6334 &-20.1300 \end{array}\displaystyle } \right ]. \end{aligned}$$

As a delayed SNN, the above-mentioned example has been widely studied in previous works [3, 4, 15, 19, 23]. For comparison, with different μ and m, the MAUBs of \(\tau(t)\) derived from [3, 4, 15, 19] and Theorem 1 proposed in this paper are summarized in Table 2. It can also be concluded from Table 2 that the results proposed in this paper are less conservative than those in [3, 4, 15, 19]. For initial state condition \([-1,1,0.4]^{\mathrm{T}}\), \(\mu=0.1\), and \(\tau=1.12\), Figure 2 depicts the state trajectories of the given SNN with activation functions \(f_{1}(s)=0.1840(|s+1|-|s-1|)\), \(f_{2}(s)=0.0897(|s+1|-|s-1|)\), \(f_{3}(s)=0.1438(|s+1|-|s-1|)\) and time-varying delay \(\tau(t) =0.56(1-\sin (0.178t))\). Figure 2 also shows that the MAUBs listed in Table 2 are capable of guaranteeing asymptotical stability of the considered SNNs with the given parameters.

Figure 2
figure 2

The state responses of the SNNs in Example 2 .

Full size image

From the two aforementioned examples, it is also concluded from Tables 1 and 2 that the conservatism is gradually reduced with the increase of delay-partitioning number m. However, as m increases, testing the proposed results is much time-consuming since the more numbers of LMIs and LMI scalar decision variables are included in the corresponding criterion. So, one can choose the appropriate m for a tradeoff between the better results and the computational efficiency [45].

5 Conclusions

Combining delay-partitioning approach with tighter bounding inequalities, this paper develops further less conservative stability criteria for GNNs with time-varying delay. A newly augmented LKF with triple integral terms is established by partitioning the delay in integral terms. The \([P_{ij}]_{(m+1)\times(m+1)}\)-dependent sub-LKF is also introduced so as to take full consideration of the relationships between the augmented state vectors. Less conservative delay-dependent stability criteria have been established in terms of \(e_{s}\) and LMIs by utilizing a Wirtinger-based integral inequality, Peng-Park’s integral inequality, and an auxiliary function-based integral inequality to effectively handle the cross-product terms appearing in derivative of the LKF. Finally, two numerical examples are provided to demonstrate the less conservatism and effectiveness of the proposed results.