Formulation and solution to time-fractional generalized Korteweg-de Vries equation via variational methods

Abstract

This paper presents the formulation of the time-fractional generalized Korteweg-de Vries equation (KdV) using the Euler-Lagrange variational technique in the Riemann-Liouville derivative sense and derives an approximate solitary wave solution. Our results show that He’s variational-iteration method is a very efficient technique for finding the solution of the proposed equation and extend the existing results.

1 Introduction

The KdV equation has been used to describe a wide range of physics phenomena of the evolution and interaction of nonlinear waves. It was derived from the propagation of dispersive shallow water waves and is widely used in fluid dynamics, aerodynamics, continuum mechanics, as a model for shock wave formation, solitons, turbulence, boundary layer behavior, mass transport, and the solution representing the water’s free surface over a flat bed [1–3]. Camassa and Holm [4] put forward the derivation of solution as a model for dispersive shallow water waves and discovered that it is a formally integrable dimensional Hamiltonian system, and that its solitary waves are solitons. Most of the classical mechanics techniques have been used in studies of conservative systems, but most of the processes observed in the physical real world are nonconservative.

During the past three decades or so, fractional calculus has obtained considerable popularity and importance as generalization of integer-order evolution equations, and one has used it to model some meaningful things, such as fractional calculus in model price volatility in finance [5, 6], in hydrology to model fast spreading of pollutants [7]; the most common hydrologic application of fractional calculus is the generation of fractional Brownian motion as a representation of aquifer material with a long-range correlation structure [8, 9]. The fractional differential equation is used to model the particle motions in a heterogeneous environment and long particle jumps in anomalous diffusion in physics [10, 11]. For other exact descriptions of the applications of engineering, mechanics, mathematics, etc., we can refer to [12–16]. If the Lagrangian of conservative system is constructed using fractional derivatives, the resulting equations of motion can be nonconservative. Therefore, in many cases, real physical processes could be modeled in a reliable manner using fractional-order differential equations rather than integer-order equations [17]. Based on the stochastic embedding theory, Cresson [18] defined the fractional embedding of differential operators and provided a fractional Euler-Lagrange equation for Lagrangian systems, then investigated a fractional Noether theorem and a fractional Hamiltonian formulation of fractional Lagrangian systems. Herzallah and Baleanu [19] presented the necessary and sufficient optimality conditions for the Euler-Lagrange fractional equations of fractional variational problems and made an effort in determining in which spaces the functional must exist. Malinowska [20] proposed the Euler-Lagrange equations for fractional variational problems with multiple integrals and proved the fractional Noether-type theorem for conservative and nonconservative generalized physical systems. Riewe [21, 22] formulated a version of the Euler-Lagrange equation for problems of calculus of variation with fractional derivatives. Wu and Baleanu [23] developed some new variational-iteration formulas to find approximate solutions of fractional differential equations and determined the Lagrange multiplier in a more accurate way. For generalized fractional Euler-Lagrange equations and a fractional-order Van der Pol-like oscillator, we can refer to the works by Odzijewicz [24, 25] and Attari et al. [26], respectively. For other the known results refer to Baleanu et al. [27] and Inokuti et al. [28]. In view of the fact that most physical phenomena may be considered as nonconservative, they can be described using fractional-order differential equations. Recently, several methods have been used to solve nonlinear fractional evolution equations using techniques of nonlinear analysis, such as the Adomian decomposition method [29], the homotopy analysis method [30, 31], the homotopy perturbation method [32, 33] and the Laguerre spectral method [34–36]. It was mentioned that the variational-iteration method has been used successfully to solve different types of integer and fractional nonlinear evolution equations.

In the present paper, He’s variational-iteration method [37–40] is applied to solve the time-fractional generalized KdV equation

$${}_0{}^{R}D_t^{\alpha }u(x,t)+a{u}^p(x,t)u_x(x,t)+b{u}_{xxx}(x,t)=0,$$

where a, b are constants, $u(x,t)$ is a field variable, the subscripts denote the partial differentiation of the function $u(x,t)$ with respect to the parameter x and t. $x\in \mathrm{\Omega }$ ($\mathrm{\Omega }\subseteq \mathbb{R}$) is a space coordinate in the propagation direction of the field and $t\in T$ ($=[0,t_0]$ ($t_0>0$)) is the time, which occurs in different contexts in mathematical physics. a, b are constant coefficients not equal to zero. The dissipative $u_{xxx}$ term provides dam** at small scales, and the nonlinear term $u^p{u}_x$ ($p>0$) (which has the same form as that in the KdV or 1-dimensional Navier-Stokes equations) stabilizes by transferring energy between large and small scales. For $p=1$, we can refer to the known results of the time-fractional KdV equation: formulation and solution using variational methods [41, 42]. For $p>0$, $p\ne 1$, there is little material on the formulation and solution to time-fractional KdV equation. Thus the present paper considers the formulation and solution to a time-fractional KdV equation as the index of the nonlinear term satisfies $p>0$, $p\ne 1$. ${}_0{}^{R}D_t^{\alpha }$ denotes the Riesz fractional derivative. Making use of the variational-iteration method, this work is devoted to a formulation of a time-fractional generalized KdV equation and derives an approximate solitary wave solution.

This paper is organized as follows: Section 2 states some background material from fractional calculus. Section 3 presents the principle of He’s variational-iteration method. Section 4 is devoted to a description of the formulation of the time-fractional generalized KdV equation using the Euler-Lagrange variational technique and to derive an approximate solitary wave solution. Section 5 presents an analysis for the obtained graphs and figures and discusses the present work.

2 Preliminaries

We recall the necessary definitions for the fractional calculus (see [43–45]) which are used throughout the remaining sections of this paper.

Definition 1 A real multivariable function $f(x,t)$, $t>0$ is said to be in the space $C_{\gamma }$, $\gamma \in \mathbb{R}$ with respect to t if there exists a real number r (>γ), such that $f(x,t)=t^r{f}_1(x,t)$, where $f_1(x,t)\in C(\mathrm{\Omega }\times T)$. Obviously, $C_{\gamma }\subset C_{\delta }$ if $\delta \le \gamma$.

Definition 2 The left-hand side Riemann-Liouville fractional integral of a function $f\in C_{\gamma }$ ($\gamma \ge -1$) is defined by

$$\begin{array}{c}{}_{0}I_t^{\alpha }f(x,t)=\frac{1}{\mathrm{\Gamma }(\alpha )}{\int }_0^t\frac{f(x,\tau )}{{(t-\tau )}^{1-\alpha }}d\tau ,\alpha >0,t\in T,\hfill \\ {}_{0}I_t^{0}f(x,t)=f(x,t).\hfill \end{array}$$

Definition 3 The Riemann-Liouville fractional derivatives of the order $n-1\le \alpha <n$ of a function $f\in C_{\gamma }$ ($\gamma \ge -1$) are defined as

$$\begin{array}{c}{}_{0}D_t^{\alpha }f(x,t)=\frac{1}{\mathrm{\Gamma }(n-\alpha )}\frac{{\partial }^n}{\partial t^n}{\int }_0^t\frac{f(x,\tau )}{{(t-\tau )}^{\alpha +1-n}}d\tau ,\hfill \\ {}_{t}D_{t_0}^{\alpha }f(x,t)=\frac{1}{\mathrm{\Gamma }(n-\alpha )}\frac{{\partial }^n}{\partial t^n}{\int }_t^{t_0}\frac{f(x,\tau )}{{(\tau -t)}^{\alpha +1-n}}d\tau ,t\in T.\hfill \end{array}$$

Lemma 1 The integration formula of Riemann-Liouville fractional derivative for the order $0<\alpha <1$

$${\int }_{T}f{(x,t)}_0{D}_t^{\alpha }g(x,t)dt={\int }_{T}g{(x,t)}_t{D}_{t_0}^{\alpha }f(x,t)dt$$

is valid under the assumptions that $f,g\in C(\mathrm{\Omega }\times T)$ and that for arbitrary $x\in \mathrm{\Omega }$, ${}_{t}D_{t_0}^{\alpha }f$, ${}_{0}D_t^{\alpha }g$ exist at every point $t\in T$ and are continuous in t.

Definition 4 The Riesz fractional integral of the order $n-1\le \alpha <n$ of a function $f\in C_{\gamma }$ ($\gamma \ge -1$) is defined as

$${}_0{}^{R}I_t^{\alpha }f(x,t)=\frac{1}{2}{(}_0{I}_t^{\alpha }f(x,t){+}_t{I}_{t_0}^{\alpha }f(x,t))=\frac{1}{2\mathrm{\Gamma }(\alpha )}{\int }_0^{t_0}{|t-\tau |}^{\alpha -1}f(x,\tau )d\tau ,$$

where ${}_{0}I_t^{\alpha }$ and ${}_{t}I_{t_0}^{\alpha }$ are, respectively, the left- and right-hand side Riemann-Liouville fractional integral operators.

Definition 5 The Riesz fractional derivative of the order $n-1\le \alpha <n$ of a function $f\in C_{\gamma }$ ($\gamma \ge -1$) is defined by

$$\begin{array}{rl}{}_0{}^{R}D_t^{\alpha }f(x,t)& =\frac{1}{2}{(}_0{D}_t^{\alpha }f(x,t)+(-1)^n{}_t{D}_{t_0}^{\alpha }f(x,t))\\ =\frac{1}{2\mathrm{\Gamma }(n-\alpha )}\frac{d^n}{d{t}^n}{\int }_0^{t_0}{|t-\tau |}^{n-\alpha -1}f(x,\tau )d\tau ,\end{array}$$

where ${}_{0}D_t^{\alpha }$ and ${}_{t}D_{t_0}^{\alpha }$ are, respectively, the left- and right-hand side Riemann-Liouville fractional differential operators.

Lemma 2 Let $\alpha >0$ and $\beta >0$ be such that $n-1<\alpha <n$, $m-1<\beta <m$ and $\alpha +\beta <n$, and let $f\in L_1(\mathrm{\Omega }\times T)$ and ${}_{0}I_t^{m-\alpha }f\in A{C}^m(\mathrm{\Omega }\times T)$. Then we have the following index rule:

$${}_0{}^{R}D_t^{\alpha }{(}_0^R{D}_t^{\beta }f(x,t)){=}_0^R{D}_t^{\alpha +\beta }f(x,t)-{\sum _{i=1}^m}_0^R{D}_t^{\beta -i}f(x,t){|}_{t=0}\frac{t^{-\alpha -i}}{\mathrm{\Gamma }(1-\alpha -i)}.$$

Remark 1 One can express the Riesz fractional differential operator ${}_0{}^{R}D_t^{\alpha -1}$ of the order $0<\alpha <1$ as the Riesz fractional integral operator ${}_0{}^{R}I_{\tau }^{1-\alpha }$, i.e.

$${}_0{}^{R}D_t^{\alpha -1}f(x,t){=}_0^R{I}_t^{1-\alpha }f(x,t),t\in T.$$

3 Variational-iteration method

The variational-iteration method provides an effective procedure for explicit and solitary wave solutions of a wide and general class of differential systems representing real physical problems. Moreover, the variational-iteration method can overcome the foregoing restrictions and limitations of approximate techniques so that it provides us with a possibility to analyze strongly nonlinear evolution equations. Therefore, we extend this method to solve the time-fractional KdV equation. The basic features of the variational-iteration method are outlined as follows.

We consider a nonlinear evolution equation that consists of a linear part $\mathcal{L}u(x,t)$, a nonlinear part $\mathcal{N}u(x,t)$, and a free term $g(x,t)$ represented as

$$\mathcal{L}u(x,t)+\mathcal{N}u(x,t)=g(x,t).$$

(1)

According to the variational-iteration method, the $(n+1)$th approximation solution of (1) can be read using an iteration correction functional as

$$u_{n+1}(x,t)=u_n(x,t)+{\int }_0^t\lambda (\tau )(\mathcal{L}\tilde{u}(x,\tau )+\mathcal{N}\tilde{u}(x,\tau )-g(x,\tau ))d\tau ,$$

(2)

where $\lambda (\tau )$ is a Lagrangian multiplier and $\tilde{u}(x,t)$ is considered as a restricted variation function, i.e., $\delta \tilde{u}(x,t)=0$. Extremizing the variation of the correction functional (2) leads to the Lagrangian multiplier $\lambda (\tau )$. The initial iteration $u_0(x,t)$ can be used as the initial value $u(x,0)$. As n tends to infinity, the iteration leads to the solitary wave solution of (1), i.e.

$$u(x,t)=\underset{n\to \mathrm{\infty }}{lim}{u}_n(x,t).$$

4 Time-fractional generalized KdV equation

The generalized KdV equation in $(1+1)$ dimensions is given by

$$u_t(x,t)+a{u}^p(x,t)u_x(x,t)+b{u}_{xxx}(x,t)=0,$$

(3)

where $p>0$, a, b are constants, $u(x,t)$ is a field variable, $x\in \mathrm{\Omega }$ is a space coordinate in the propagation direction of the field and $t\in T$ is the time. Employing a potential function $v(x,t)$ on the field variable, setting $u(x,t)=v_x(x,t)$, yields the potential equation of the generalized KdV equation (3) in the form

$$v_{xt}(x,t)+a{v}_x^p(x,t)v_{xx}(x,t)+b{v}_{xxxx}(x,t)=0.$$

(4)

The Lagrangian of this generalized KdV equation (3) can be defined using the semi-inverse method [46, 47] as follows. The functional of the potential equation (4) can be represented as

$$J(v)={\int }_{\mathrm{\Omega }}dx{\int }_T(v(x,t)(c_1{v}_{xt}(x,t)+c_{2}a{v}_x^p(x,t)v_{xx}(x,t)+c_{3}b{v}_{xxxx}(x,t)))dt,$$

(5)

with $c_i$ ($i=1,2,3$) being unknown constants to be determined later. Integrating (5) by parts and taking $v_t{|}_{\mathrm{\Omega }}=v_x{|}_{\mathrm{\Omega }}=v_x{|}_T=0$ yield

$$\begin{array}{rcl}J(v)& =& {\int }_{\mathrm{\Omega }}dx{\int }_T(-c_1{v}_x(x,t)v_t(x,t)-\frac{c_{2}a}{p+1}{v}_x^{p+2}(x,t)\\ -c_{3}b{v}_x(x,t)v_{xxx}(x,t))dt.\end{array}$$

(6)

The constants $c_i$ ($i=1,2,\dots ,6$) can be determined taking the variation of the functional (6) to make it optimal. By applying the variation of the functional, integrating each term by parts, and making use of the variation optimum condition of the functional $J(v)$, it yields the following expression:

$$-2c_1{v}_{xt}(x,t)-c_{2}a(p+2)v_x^p(x,t)v_{xx}(x,t)-2c_{3}b{v}_{xxxx}(x,t)=0.$$

(7)

We notice that the obtained result (7) is equivalent to (4), so one sees that the constants $c_i$ ($i=1,2,\dots ,6$) are, respectively,

$$c_1=-\frac{1}{2},c_2=-\frac{1}{p+2},c_3=-\frac{1}{2}.$$

In addition, the functional expression given by (6) obtains directly the Lagrangian form of the generalized KdV equation,

$$\begin{array}{rcl}L(v_t,v_x,v_{xxx})& =& \frac{1}{2}{v}_x(x,t)v_t(x,t)+\frac{a}{(p+1)(p+2)}{v}_x^{p+2}(x,t)\\ +\frac{b}{2}{v}_x(x,t)v_{xxx}(x,t).\end{array}$$

Similarly, the Lagrangian of the time-fractional version of the generalized KdV equation could be read as

$$\begin{array}{rcl}F{(}_0{D}_t^{\alpha }v,v_x,v_{xxx})& =& \frac{1}{2}{v}_x{(x,t)}_0{D}_t^{\alpha }v(x,t)+\frac{a}{(p+1)(p+2)}{v}_x^{p+2}(x,t)\\ +\frac{b}{2}{v}_x(x,t)v_{xxx}(x,t),\alpha \in ]0,1].\end{array}$$

(8)

Then the functional of the time-fractional generalized KdV equation will take the form of the expression

$$J(v)={\int }_{\mathrm{\Omega }}dx{\int }_{T}F{(}_0{D}_t^{\alpha }v,v_x,v_{xxx})dt,$$

(9)

where the time-fractional Lagrangian $F{(}_0{D}_t^{\alpha }v,v_x,v_{xxx})$ is given by (8). Following Agrawal’s method [48–50], the variation of the functional (9) with respect to $v(x,t)$ leads to

$$\begin{array}{rcl}\delta J(v)& =& {\int }_{\mathrm{\Omega }}dx{\int }_T(\frac{\partial F}{{\partial }_0{D}_t^{\alpha }v}\delta {(}_0{D}_t^{\alpha }v(x,t))+\frac{\partial F}{\partial v_x}\delta v_x(x,t)\\ +\frac{\partial F}{\partial v_{xxx}}\delta v_{xxx}(x,t))dt.\end{array}$$

(10)

By Lemma 1, upon integrating the right-hand side of (10), one has

$$\delta J(v)={\int }_{\mathrm{\Omega }}dx{\int }_T{(}_t{D}_T^{\alpha }\left(\frac{\partial F}{{\partial }_0{D}_t^{\alpha }v}\right)-\frac{\partial }{\partial x}\left(\frac{\partial F}{\partial v_x}\right)-\frac{{\partial }^3}{\partial x^3}\left(\frac{\partial F}{\partial v_{xxx}}\right))\delta vdt,$$

noting that $\delta v{|}_T=\delta v{|}_{\mathrm{\Omega }}=\delta v_x{|}_{\mathrm{\Omega }}=0$.

Obviously, optimizing the variation of the functional $J(v)$, i.e., $\delta J(v)=0$, yields the Euler-Lagrange equation for time-fractional generalized KdV equation as in the following expression:

$${}_{t}D_T^{\alpha }\left(\frac{\partial F}{{\partial }_0{D}_t^{\alpha }v}\right)-\frac{\partial }{\partial x}\left(\frac{\partial F}{\partial v_x}\right)-\frac{{\partial }^3}{\partial x^3}\left(\frac{\partial F}{\partial v_{xxx}}\right)=0.$$

(11)

Substituting the Lagrangian of the time-fractional generalized KdV equation (8) into the Euler-Lagrange formula (11) one obtains

$${}_{t}D_T^{\alpha }(\frac{1}{2}{v}_x(x,t)){-}_0{D}_t^{\alpha }(\frac{1}{2}{v}_x(x,t))-a{v}_x^p(x,t)v_{xx}(x,t)-b{v}_{xxxx}(x,t)=0.$$

Once again, substituting the potential function $v_x(x,t)$ for $u(x,t)$ yields the time-fractional generalized KdV equation for the state function $u(x,t)$,

$$\frac{1}{2}{(}_0{D}_t^{\alpha }u(x,t){-}_t{D}_T^{\alpha }u(x,t))+a{u}^p(x,t)u_x(x,t)+b{u}_{xxx}(x,t)=0.$$

(12)

According to the Riesz fractional derivative ${}_0{}^{R}D_t^{\alpha }u(x,t)$, the time-fractional generalized KdV equation represented in (12) can be written as

$${}_0{}^{R}D_t^{\alpha }u(x,t)+a{u}^p(x,t)u_x(x,t)+b{u}_{xxx}(x,t)=0.$$

(13)

Acting from the left-hand side by the Riesz fractional operator ${}_0{}^{R}D_t^{1-\alpha }$ on (13) leads to

$$\begin{array}{c}\frac{\partial }{\partial t}u(x,t){-}_0^R{D}_t^{\alpha -1}u(x,t){|}_{t=0}\frac{t^{\alpha -2}}{\mathrm{\Gamma }(\alpha -1)}\hfill \\ {+}_0^R{D}_t^{1-\alpha }(a{u}^p(x,t)\frac{\partial }{\partial x}u(x,t)+b\frac{{\partial }^3}{\partial x^3}u(x,t))=0,\hfill \end{array}$$

(14)

from Lemma 2. In view of the variational-iteration method, combining with (14), the $(n+1)$th approximate solution of (13) can be read using the iteration correction functional as

$$\begin{array}{rcl}{u}_{n+1}(x,t)& =& u_n(x,t)+{\int }_0^t\lambda (\tau )[\frac{\partial }{\partial \tau }{u}_n(x,\tau ){-}_0^R{D}_{\tau }^{\alpha -1}{u}_n(x,\tau ){|}_{\tau =0}\frac{{\tau }^{\alpha -2}}{\mathrm{\Gamma }(\alpha -1)}\\ {+}_0^R{D}_{\tau }^{1-\alpha }(a{\tilde{u}}_n^p(x,\tau )\frac{\partial }{\partial x}{\tilde{u}}_n(x,\tau )+b\frac{{\partial }^3}{\partial x^3}{\tilde{u}}_n(x,\tau ))]d\tau ,n\ge 0,\end{array}$$

(15)

where the function ${\tilde{u}}_n(x,t)$ is considered as a restricted variation function, i.e., $\delta {\tilde{u}}_n(x,t)=0$. The extremum of the variation of (15) subject to the restricted variation function straightforwardly yields

$$\begin{array}{rl}\delta u_{n+1}(x,t)& =\delta u_n(x,t)+{\int }_0^t\lambda (\tau )\delta \frac{\partial }{\partial \tau }{u}_n(x,\tau )d\tau \\ =\delta u_n(x,t)+\lambda (\tau )\delta u_n(x,\tau ){|}_{\tau =t}-{\int }_0^t\frac{\partial }{\partial \tau }\lambda (\tau )\delta u_n(x,\tau )d\tau \\ =0.\end{array}$$

This expression reduces to the following stationary conditions:

$$\frac{\partial }{\partial \tau }\lambda (\tau )=0,1+\lambda (\tau )=0,$$

which are converted to the Lagrangian multiplier at $\lambda (\tau )=-1$. Therefore, the correction functional (15) takes the following form:

$$\begin{array}{rcl}{u}_{n+1}(x,t)& =& u_n(x,t)-{\int }_0^t[\frac{\partial }{\partial \tau }{u}_n(x,\tau ){-}_0^R{I}_{\tau }^{1-\alpha }{u}_n(x,\tau ){|}_{\tau =0}\frac{{\tau }^{\alpha -2}}{\mathrm{\Gamma }(\alpha -1)}\\ {+}_0^R{D}_{\tau }^{1-\alpha }(a{u}_n^p(x,\tau )\frac{\partial }{\partial x}{u}_n(x,\tau )+b\frac{{\partial }^3}{\partial x^3}{u}_n(x,\tau ))]d\tau ,n\ge 0,\end{array}$$

(16)

and since $\alpha -1<0$, the fractional derivative operator ${}_0{}^{R}D_t^{\alpha -1}$ reduces to the fractional integral operator ${}_0{}^{R}I_t^{1-\alpha }$ by Remark 1.

The right-hand side Riemann-Liouville fractional derivative is interpreted as a future state of the process in physics. For this reason, the right-derivative is usually neglected in applications, when the present state of the process does not depend on the results of the future development, and so the right-derivative is used equal to zero in the following calculations. The zeroth order solitary wave solution can be taken as the initial value of the state variable, which is taken in this case as

$$u_0(x,t)=u(x,0)=k{sech}^{\frac{2}{p}}(\frac{p}{2\sqrt{b}}(x+{\eta }_0)),$$

where $k={(\frac{(p+1)(p+2)}{2a})}^{\frac{1}{p}}$, ${\eta }_0$ is a constant.

Substituting this zeroth order approximation solitary wave solution into (16) and using Definition 5 lead to the first order approximate solitary wave solution

$$u_1(x,t)=k{sech}^{\frac{2}{p}}(\frac{p}{2\sqrt{b}}(x+{\eta }_0))(1+\frac{t^{\alpha }}{\sqrt{b}\mathrm{\Gamma }(\alpha +1)}tanh(\frac{p}{2\sqrt{b}}(x+{\eta }_0))).$$

Substituting the first order approximate solitary wave solution into (16), using Definition 5 then leads to the second order approximate solitary wave solution in the following form:

$$\begin{array}{rcl}{u}_2(x,t)& =& k{sech}^{\frac{2}{p}}(\frac{p}{2\sqrt{b}}(x+{\eta }_0))\\ +\frac{t^{\alpha }}{\mathrm{\Gamma }(\alpha +1)}[\frac{a{k}^{p+1}}{\sqrt{b}}{sech}^{\frac{2}{p}+2}(\frac{p}{2\sqrt{b}}(x+{\eta }_0))tanh(\frac{p}{2\sqrt{b}}(x+{\eta }_0))\\ +\frac{k}{\sqrt{b}}{sech}^{\frac{2}{p}}(\frac{p}{2\sqrt{b}}(x+{\eta }_0)){tanh}^3(\frac{p}{2\sqrt{b}}(x+{\eta }_0))\\ -\frac{3kp}{2\sqrt{b}}{sech}^{\frac{2}{p}+2}(\frac{p}{2\sqrt{b}}(x+{\eta }_0))-\frac{k{p}^2}{2\sqrt{b}}{sech}^{\frac{2}{p}+2}(\frac{p}{2\sqrt{b}}(x+{\eta }_0))\\ \times tanh(\frac{p}{2\sqrt{b}}(x+{\eta }_0))]\\ -\frac{t^{2\alpha }}{\mathrm{\Gamma }(2\alpha +1)}[\frac{a{k}^{p+1}}{b}{sech}^{\frac{2}{p}+2}(\frac{p}{2\sqrt{b}}(x+{\eta }_0))\\ \times (\frac{p}{2}-\frac{3p+2}{2}{tanh}^2(\frac{p}{2\sqrt{b}}(x+{\eta }_0)))\\ -\frac{3k{p}^2(p+2)}{8b}{sech}^{\frac{2}{p}}(\frac{p}{2\sqrt{b}}(x+{\eta }_0)){tanh}^2(\frac{p}{2\sqrt{b}}(x+{\eta }_0))\\ -\frac{3k{p}^2(p+2)}{8b}{sech}^{\frac{2}{p}+2}(\frac{p}{2\sqrt{b}}(x+{\eta }_0))\\ +\frac{3kp{(p+2)}^2}{8b}{sech}^{\frac{2}{p}}(\frac{p}{2\sqrt{b}}(x+{\eta }_0)){tanh}^2(\frac{p}{2\sqrt{b}}(x+{\eta }_0))\\ +\frac{k{p}^3}{8b}{sech}^{\frac{2}{p}}(\frac{p}{2\sqrt{b}}(x+{\eta }_0))\\ -\frac{k{(p+2)}^3}{8b}{sech}^{\frac{2}{p}}(\frac{p}{2\sqrt{b}}(x+{\eta }_0)){tanh}^4(\frac{p}{2\sqrt{b}}(x+{\eta }_0))\\ +\frac{3k{(p+2)}^2}{8b}{sech}^{\frac{2}{p}+2}(\frac{p}{2\sqrt{b}}(x+{\eta }_0)){tanh}^2(\frac{p}{2\sqrt{b}}(x+{\eta }_0))\\ +\frac{k{p}^2(p+2)}{4b}{sech}^{\frac{2}{p}+2}(\frac{p}{2\sqrt{b}}(x+{\eta }_0)){tanh}^2(\frac{p}{2\sqrt{b}}(x+{\eta }_0))]\\ -\frac{\mathrm{\Gamma }(2\alpha +1)t^{3\alpha }}{\mathrm{\Gamma }(3\alpha +1){(\mathrm{\Gamma }(\alpha +1))}^2}[\frac{ap{k}^{p+1}}{2b\sqrt{b}}{sech}^{\frac{2}{p}+2}(\frac{p}{2\sqrt{b}}(x+{\eta }_0))\\ \times tanh(\frac{p}{2\sqrt{b}}(x+{\eta }_0))(p-\frac{p+2}{2}{tanh}^2(\frac{p}{2\sqrt{b}}(x+{\eta }_0)))].\end{array}$$

Making use of Definition 5 and the Maple package or Mathematics, we obtain $u_3(x,t)$, $u_4(x,t)$ and so on, and substituting the $n-1$ order approximate solitary wave solution into (16) leads to the n order approximate solitary wave solution. As n tends to infinity, the iteration leads to the solitary wave solution of the time-fractional generalized KdV equation

$$u(x,t)=k{sech}^{\frac{2}{p}}(\frac{p}{2\sqrt{b}}(x-t+{\eta }_0)).$$

5 Discussion

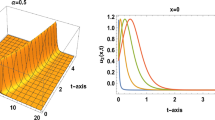
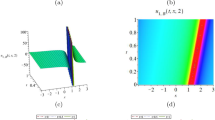
The target of the present work is the effect of the fractional-order derivative on the structure and propagation of the resulting solitary waves obtained from time-fractional generalized KdV equations. We derive the Lagrangian of the generalized KdV equations by the semi-inverse method, and then we take a similar form for the Lagrangian to the time-fractional generalized KdV equations. Using the Euler-Lagrange variational technique, we continue our calculations until the third order iteration. Meanwhile, our approximate calculations are carried out on the solution of the time-fractional generalized KdV equations taking into account the values of the coefficients and some meaningful values namely, $\alpha =1,\frac{4}{5},\frac{1}{2}\text{ and }\frac{1}{5}$. The solitary wave solution of time-fractional generalized KdV equations are obtained. In addition, a 3-dimensional representation of the solution $u(x,t)$ for the time-fractional generalized KdV equations with space x and time t for different values of the order α is presented, respectively. In Figure 1, the solution u is still a single soliton wave solution for all values of the order α. It shows that the balancing scenario between nonlinearity and dispersion is still valid. Figure 2 presents the change of amplitude and width of the soliton due to the variation of the order α, 2- and 3-dimensional graphs depicted the behavior of the solution $u(x,t)$ at time $t=1$ corresponding to different values of the order α. This behavior indicates that the increasing of the value α is uniform in both the height and the width of the solitary wave solution. That is, the order α can be used to modify the shape of the solitary wave without change of the nonlinearity and the dispersion effects in the medium. Figure 3 is devoted to the study of the expression of the relation between the amplitude of the soliton and the fractional order at different time values. These figures show that at the same time, the increasing of the fractional α increases the amplitude of the solitary wave to some value of α.

Figure 1

The function u as a 3-dimensions graph for different order α when $\mathit{p}\mathbf{=}\mathbf{3}$ , $\mathit{a}\mathbf{=}\mathbf{10}$ , $\mathit{b}\mathbf{=}\mathbf{1}$ , ${\mathit{\eta }}_{\mathbf{0}}\mathbf{=}\mathbf{0}$ .

Figure 2

u as a function of space x at time $\mathit{t}\mathbf{=}\mathbf{1}$ for different order α when $\mathit{p}\mathbf{=}\mathbf{3}$ , $\mathit{a}\mathbf{=}\mathbf{10}$ , $\mathit{b}\mathbf{=}\mathbf{1}$ , ${\mathit{\eta }}_{\mathbf{0}}\mathbf{=}\mathbf{0}$ : (A1) 3-dimensions graph, (A2) 2-dimensions graph.

Figure 3

The amplitude of the function u as a function of time t at space $\mathit{x}\mathbf{=}\mathbf{1}$ of the fractional order α when $\mathit{p}\mathbf{=}\mathbf{3}$ , $\mathit{a}\mathbf{=}\mathbf{10}$ , $\mathit{b}\mathbf{=}\mathbf{1}$ , ${\mathit{\eta }}_{\mathbf{0}}\mathbf{=}\mathbf{0}$ : (B1) 3-dimensions graph, (B2) 2-dimensions graph.

Author’s contributions

The author wrote this paper carefully, gave a rigorous derivation process, and read and approved the final manuscript.