1 Introduction

In 1998, the accelerated expansion of the universe was discovered by type Ia supernovae (SN) observations [1, 2]. The cosmic acceleration is usually explained by assuming an exotic component with negative pressure, known as dark energy [3,4,5]. In recent years, the \(\Lambda \) cold dark matter (\(\Lambda \)CDM) model, which is widely viewed as the standard model of cosmology, has been established. Measurements of cosmic microwave background (CMB) anisotropies by the Planck mission strongly favor a six-parameter base \(\Lambda \)CDM model, in which dark energy is served by the cosmological constant \(\Lambda \). However, recent advancements in the precision of cosmological parameter measurements have revealed some cracks in the \(\Lambda \)CDM model. Notably, it is found that the tension between the values of the Hubble constant inferred from the CMB observation (assuming the \(\Lambda \)CDM model) [6] and the Cepheid-supernova distance ladder measurement (model-independent) [7] has now been estimated as more than 5\(\sigma \) [7]. Recently, the Hubble tension has been intensively discussed in the literature [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24]. The Hubble tension is now commonly considered a severe crisis for cosmology [25, 26]. On one hand, the tension may herald the possibility of new physics beyond the standard \(\Lambda \)CDM model. Nevertheless, no consensus has been reached on a valid extended cosmological model that can truly solve the tension. On the other hand, the methods that can independently measure the Hubble constant need to be greatly developed to make an arbitration for the Hubble tension. The gravitational wave (GW) standard siren method is one of the most promising methods.

As proposed by Schutz in 1986, GW can be used as a standard siren to explore the cosmic expansion history [27, 28]. The absolute luminosity distance to the source could be directly obtained through the analysis of the GW waveform. If the redshift of the source can also be obtained by identifying its electromagnetic (EM) counterpart (usually referred to as a bright siren) or using statistical methods to infer the redshift information (usually referred to as a dark siren), then we can establish the true distance-redshift relation for exploring the expansion history of the universe; see e.g., Refs. [29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56]. So far, the only bright siren event, GW170817, has given the first measurement of the Hubble constant using the standard siren method with a precision of about 14% [57]. In addition, the dark siren method gives a 19% measurement precision of the Hubble constant [58]. This means that the current measurements are far from making an arbitration for the Hubble tension and researchers will have to resort to future GW observations.

Third generation (3G) ground-based GW detectors, the Einstein Telescope (ET) [59, 60] and the Cosmic Explorer (CE) [61, 62], show a powerful sensitivity, which is more than one order of magnitude improved over the current detectors [63]. Thus, in the era of 3G GW detectors, more binary neutron star (BNS) mergers will be detected at much deeper redshifts [64]. However, the detection of EM counterparts is still difficult. The observed BNS merger rate, as inferred by the LIGO–Virgo–KAGRA Collaboration, ranges from 10 to \(1700~\mathrm {Gpc^{-3}~year^{-1}}\) [65], implying that close events similar to GW170817 may occur approximately once a decade. What’s more, a single GW detector, even in a triangular configuration as planned for ET, has limited localization capabilities, giving a much larger number of galaxies per error region [66]. Fortunately, a fraction of BNS mergers (those viewed roughly on-axis) are expected to be accompanied by short \(\gamma \)-ray bursts (GRBs) and their associated afterglows, which can be accurately localized by GRB detectors. Consequently, GRB detection plays a vital role in facilitating the subsequent identification of host galaxies and the determination of redshifts.

Due to the strong beaming nature of short GRBs [67], only GRBs with small inclination angles are detectable. Recent works show that only about 0.1% of BNS mergers have detectable EM counterparts [68]. However, comprehensive forecasts for cosmological parameter estimations with 3G era GW-GRB joint observations are still absent, which deserves an in-depth investigation. In this work, we focus on the synergy of 3G GW detectors with a future GRB detector with the characteristic of the proposed Transient High-Energy Sky and Early Universe Surveyor (THESEUS) mission [69,70,71]. We constrain five typical cosmological models including the \(\Lambda \)CDM, wCDM, \(w_0w_a\)CDM, and interacting dark energy (IDE) models (I\(\Lambda \)CDM and IwCDM). Here we highlight three points of improvement in this paper: (i) We conduct a comprehensive and robust analysis of GW-GRB detection and calculate the redshift distribution of GW-GRB events instead of assuming 1000 detected standard sirens in 10-year observation, as adopted in Refs. [29,30,31,32,33,34,35,36,37,38,39,40,41,42]. (ii) For the 3G GW detectors, the impact of the Earth’s rotation is important, which includes two effects: one is the modulation of the Doppler effect quantified by the time-dependent function \(\Phi _{ij}\), and the other is quantified by the time-dependent detector responses \(F_{+,k}\) and \(F_{\times ,k}\). Therefore, we take into account the Earth’s rotation in the simulation of GW standard sirens, bringing the model closer to real observations. (iii) We conduct an analysis of the optimistic and realistic scenarios for GW-GRB detection and perform cosmological analysis, which could better show the potential of the cosmological parameter estimation using the 3G era standard sirens.

Recently, Hou et al. [48] constrained IDE models with future GW and GRB joint observation. However, they only focused on the synergy of ET alone with the THESEUS mission in the optimistic scenario for GW-GRB detection. In this paper, we make a comprehensive analysis of four different cases of 3G GW observations, single ET, single CE, the CE-CE network, and the ET-CE-CE network, by using the Fisher information matrix. Moreover, we also consider the realistic scenario for GW-GRB detection. For IDE models, we employ the extended parameterized post-Friedmann (ePPF) approach [72,73,74,75] to avoid the cosmological perturbations (see Sect. 5 for a detailed discussion).

This paper is organized as follows. In Sect. 2 we introduce a method to simulate GW standard siren data. In Sect. 3, we present the results of the prediction for GW-GRB detection. In Sect. 4, we discuss the impact of the Earth’s rotation on the luminosity distance uncertainties. In Sect. 5, we show the constraint results of cosmological parameters from the GW-GRB observations. The conclusion is given in Sect. 6. Throughout this paper, the fiducial values of cosmological parameters are set to the constraint results from CMB (Planck 2018 TT, TE, EE + lowE), baryon acoustic oscillation (BAO), and SN data. Unless otherwise specified, we set \(G = c = 1\).

2 Methodology

2.1 Cosmological models

In a flat Friedmann–Roberston–Walker universe, we can obtain the energy conservation equations,

$$\begin{aligned}&\dot{\rho }_{\textrm{de}} +3H(1+w)\rho _{\textrm{de}}= Q, \end{aligned}$$
(1)
$$\begin{aligned}&\dot{\rho }_{\textrm{c}} +3H\rho _{\textrm{c}}=-Q, \end{aligned}$$
(2)

where Q is the energy transfer rate, \(\rho _{\textrm{de}}\) and \(\rho _{\textrm{c}}\) represent the energy densities of dark energy and CDM, respectively, w is the equation of state (EoS) parameter of dark energy, H is the Hubble parameter, and the dot denotes the derivative with respect to the cosmic time t.

If \(Q=0\), it indicates no interaction between dark energy and CDM. In this work, we consider three cosmological models without interaction: (i) the \(\Lambda \)CDM model, known as the standard model of cosmology, in which dark energy is described by a cosmological constant \(\Lambda \) with \(w(z)=-1\); (ii) the wCDM model, the simplest dynamical dark energy model, in which the EoS parameter of dark energy is a constant, i.e., \(w(z)=\textrm{constant}\); (iii) the \(w_0w_a\)CDM model, the parameterized dynamical dark energy model with \(w(z)=w_0+w_{\textrm{a}}z/(1+z)\).

If \(Q\ne 0\), it means that dark energy has a direct interaction with CDM. This type of cosmological model is referred to as an IDE model. However, the microscopic nature of dark energy and dark matter is still unclear; the energy transfer rate in the IDE models can be considered in a purely phenomenological way, i.e., proportional to the energy density of dark energy, dark matter, or some mixture of them. In this work, we will consider the interaction form of \(Q=\beta H\rho _{\textrm{c}}\), where \(\beta \) is the dimensionless coupling parameter. Here \(\beta >0\) and \(\beta <0\) mean CDM decaying into dark energy and dark energy decaying into CDM, respectively.

2.2 Simulation of BNS mergers

In order to generate a catalog of BNS coalescences, we first calculate a redshift distribution of the BNS mergers. It is drawn from a normalized probability distribution,

$$\begin{aligned} p(z)=\frac{R_{\textrm{m}}(z)}{\int _{0}^{10}R_{\textrm{m}}(z)\textrm{d}z}, \end{aligned}$$
(3)

where \(R_{\textrm{m}}(z)\) is the BNS merger rate with redshift z in the observer frame. It can be estimated by

$$\begin{aligned} R_{\textrm{m}}(z)=\frac{\mathcal {R}_{\textrm{m}}(z)}{1+z} \frac{\textrm{d}V(z)}{\textrm{d}z}, \end{aligned}$$
(4)

where \(\textrm{d}V/\textrm{d}z\) is the comoving volume element and \(\mathcal {R}_\textrm{m}(z)\) is the BNS merger rate in the source frame.

A BNS merger can be thought of as occurring with a delay timescale with respect to the BNS formation history, which is given by

$$\begin{aligned} \mathcal {R}_{\textrm{m}}(z)=\int _{t_{\textrm{min}}}^{t_{\textrm{max}}} \mathcal {R}_{\textrm{f}}[t(z)-t_{\textrm{d}}] P(t_{\textrm{d}})\textrm{d}t_{\textrm{d}}, \end{aligned}$$
(5)

where \(P(t_{\textrm{d}})\) is the delay time distribution which encodes the time span between the formation of the BNS system until the two NSs merge through the emission of GWs and GRBs. \(t_{\textrm{d}}\) is the time delay between the formation of BNS system and merger, t(z) is the age of the universe at the time of merger, \(t_{\textrm{min}}=20\) Myr is the minimum delay time, \(t_{\textrm{max}}=t_{\textrm{H}}\) is the Hubble time, which stands for a maximum delay time [76], and \(\mathcal {R}_{\textrm{f}}\) is the BNS formation rate.

Here, we assume that \(\mathcal {R}_{\textrm{f}}\) is simply proportional to the star formation rate density:

$$\begin{aligned} \mathcal {R}_{\textrm{f}}\equiv \lambda \psi _{\mathrm{{MD}}}, \end{aligned}$$
(6)

where \(\psi _{\mathrm{{MD}}}\) is the Madau–Dickinson star formation rate [77] and \(\lambda \) is the currently unknown BNS mass efficiency (assumed not to evolve with redshift) used as a free parameter [78], determined by the local comoving merger rate \(\mathcal {R}_{\textrm{m}}(z=0)\).

Main types of delay time distributions include the Gaussian delay model [79], log-normal delay model [80, 81], exponential time delay model [82, 83], and power-law delay model [79, 84]. For simplicity, we only adopt the exponential time delay model as our delay time model, which is given by [82, 83]

$$\begin{aligned} P(t_{\textrm{d}})=\frac{1}{\tau }\textrm{exp}(-t_{\textrm{d}}/\tau ), \end{aligned}$$
(7)

with \(\tau =100\) Myr for \(t_{\textrm{d}}>t_{\textrm{min}}\).

In our calculations, we adopt the local comoving merger rate to be 920 \(\mathrm Gpc^{-3}~year^{-1}\) estimated from the O1 LIGO and the O2 LIGO/Virgo observation run [85]. This is also consistent with the latest O3 observation run [65]. We simulate a catalog of BNS mergers for 10 years. For each source, the location \((\theta ,\phi )\), the cosine of the inclination angle \(\iota \), the polarization angle \(\psi \), and the coalescence phase \(\psi _{\textrm{c}}\) are drawn from uniform distributions. For the masses in a BNS system, we assume that each component is drawn independently from a common Gaussian distribution, based on the NS masses observed in Galactic BNSs. This distribution has a mean of 1.33 \(M_{\odot }\) and a standard deviation of 0.09 \(M_{\odot }\) [85, 86].

It should be noted that when simulating the catalog of BNS coalescences, we randomly select relevant parameters within reasonable ranges consistent with the O3 observing run [65]. Therefore, we must admit that it is challenging to fully eliminate the influence of significant stochastic fluctuations on the constraints on cosmological parameters. The primary goal of this paper is to illustrate the significant potential that lies in the collaborative observations between 3G GW detectors and future GRB detectors in refining our understanding of cosmological studies.

2.3 Detection of GW events

In this section, we briefly review the operational details of a GW detector network. We use the vector \(r_k\) with \(k=1,2,\ldots ,N\) to denote the spatial locations of the detectors, which is given by

$$\begin{aligned} \varvec{r}_k=R_{\oplus }(\sin \varphi _k\cos \alpha _k,\sin \varphi _k\sin \alpha _k,\cos \varphi _k), \end{aligned}$$
(8)

where \(R_{\oplus }\) is the radius of the Earth, \(\varphi _k\) is the latitude of the detector in the celestial system. Here we define \(\alpha _k\) as \(\alpha _k\equiv \lambda _k+\Omega _{\textrm{r}}t\), where \(\lambda _k\) is the East longitude of the detector, \(\Omega _{\textrm{r}}\) is the rotational angular velocity of the Earth. In this paper, we take the zero Greenwich sidereal time as \(t=0\).

Let us begin by considering the long-wavelength approximation. Under this approximation, the antenna response is purely a projection effect that maps the strains in the wave-frame onto the detector [87].Footnote 1 For a transverse-traceless GW signal detected by a single detector labeled k, the response is given by

$$\begin{aligned} h_k(t_{0}+\varvec{\tau }_k+t)=F_{+,k}h_{+}(t)+F_{\times ,k}h_{\times }(t), \quad 0<t<T, \nonumber \\ \end{aligned}$$
(9)

where \(t_{0}\) is the arrival time of the GW at the coordinate origin, \(\varvec{\tau }_k=\varvec{n}\cdot \varvec{r}_k(t)\) is the time required for the GW to travel from the origin to reach the k-th detector at time t. Here \(t\in [0,T]\) is the time label of GW, T is the signal duration, and \(\varvec{n}\) is the propagation direction of a GW event. As mentioned above, \(h_{+}\) and \(h_{\times }\) are the plus and cross modes of GW, respectively. The quantities \(F_{+,k}\) and \(F_{\times ,k}\) are the k-th detector’s antenna response functions of two polarizations, which depend on the location of the source, the polarization angle, and the specific geometry parameters of the GW detector (the latitude \(\varphi \), the longitude \(\lambda \) of the detector’s vertex, the opening angle \(\zeta \) between the detector’s two arms, and the orientation angle \(\gamma \) of the detector’s arms measured counter-clockwise from East to the bisector of the interferometer arms) [87].

Under the stationary phase approximation (SPA), the frequency-domain GW waveform considering the detector network including N independent detectors can be written as [89]

$$\begin{aligned} \tilde{\varvec{h}}(f)=\textrm{e}^{-i\varvec{\Phi }}\varvec{h}(f), \end{aligned}$$
(10)

where \(\varvec{\Phi }\) is the \(N\times N\) diagonal matrix with \(\Phi _{ij}=2\pi f\delta _{ij}(\varvec{n\cdot r}_i(f))\), and

$$\begin{aligned} \begin{aligned} \varvec{h}(f)&=\left[ \frac{h_1(f)}{\sqrt{S_{\mathrm{{n}},1}(f)}}, \frac{h_2(f)}{\sqrt{S_{\mathrm{{n}},2}(f)}}, \ldots ,\frac{h_k(f)}{\sqrt{S_{\textrm{n},k}(f)}},\right. \\&\quad \ \left. \ldots ,\frac{h_N(f)}{\sqrt{S_{\textrm{n},N}(f)}}\right] ^\textrm{T}, \end{aligned} \end{aligned}$$
(11)

where \(h_k(f)\) is the frequency domain GW waveform and \(S_{\textrm{n},k}(f)\) is the one-side noise power spectral density of the k-th detector. In this paper, we consider the waveform in the inspiralling stage for a BNS system and neglect the NS spins, which are believed to have small effect on the GW waveform of BNS systems [90]. We adopt the restricted post-Newtonian approximation and calculate the waveform to the 3.5 PN order. The SPA Fourier transform of GW waveform of the k-th detector is given by [91]

$$\begin{aligned} h_k(f)=&\mathcal A_k f^{-7/6}\textrm{exp} \{i[2\pi f t_{\textrm{c}}-\pi /4-2\psi _c+2\Psi (f/2)]\nonumber \\ {}&-\varphi _{k,(2,0)}\}, \end{aligned}$$
(12)

where the Fourier amplitude \(\mathcal A_k\) is given by

$$\begin{aligned} \mathcal A_k=&\frac{1}{d_\textrm{L}}\sqrt{(F_{+,k}(1+\cos ^{2}\iota ))^{2}+(2F_{\times ,k}\cos \iota )^{2}}\nonumber \\&\times \sqrt{5\pi /96}\pi ^{-7/6}\mathcal M^{5/6}_{\textrm{chirp}}, \end{aligned}$$
(13)

where \(d_{\textrm{L}}\) is the luminosity distance to the source, \(\mathcal M_{\textrm{chirp}}\) is the chirp mass of the binary system, and the detailed forms of \(\psi (f/2)\) and \(\varphi _{k,(2,0)}\) can be found in Refs. [92, 93]. Under SPA, \(F_{+,k}\), \(F_{\times ,k}\) and \(\Phi _{ij}\) are all functions with respect to frequency, which are given by

$$\begin{aligned} \begin{aligned}&F_{+,k}(f)=F_{+,k}(t=t_{\textrm{f}}), ~~~~F_{\times ,k}(f)=F_{\times ,k}(t=t_{\textrm{f}}),\\&\Phi _{ij}(f)=\Phi _{ij}(t=t_{\textrm{f}}), \end{aligned} \end{aligned}$$
(14)

where \(t_{\textrm{f}}=t_{\textrm{c}}-(5/256)\mathcal M^{-5/3}_{\textrm{chirp}}(\pi f)^{-8/3}\) and \(t_{\textrm{c}} \in [0,10]\) year is the coalescence time [94].

The term \(t_{\textrm{f}}\), which is mentioned above, represents the effect of the movement of the Earth during the time of the GW signal. If this effect is ignored, \(t_{\textrm{f}}\) can be approximately treated as a constant for a given GW event. For binary coalescence, the duration of the signal \(t_*\) in a detector band is a strong function of the detector’s low-frequency cutoff \(f_\textrm{lower}\) [94],

$$\begin{aligned} t_*=0.86~\textrm{day} \left( \frac{1.21~M_{\odot }}{\mathcal {M}_\textrm{chirp}}\right) ^{5/3} \left( \frac{2~\textrm{Hz}}{f_\textrm{lower}}\right) ^{8/3}. \end{aligned}$$
(15)

For 3G GW detectors, \(f_{\textrm{lower}}\) is extended to about 1 Hz. For the BNS with \(m_1=m_2=1.4~M_{\odot }\), we have \(t_*=5.44~\textrm{days}\). Therefore, the impact of the Earth’s rotation is important. For this reason, we consider this effect in our analysis.

Having the BNS coalescence catalog, we can easily determine whether its generated GW emission could be detected by GW detectors. Here we adopt the signal-to-noise ratio (SNR) threshold to be 12.Footnote 2 For low-mass systems, the combined SNR for the detection network of N independent detectors is given by

$$\begin{aligned} \rho =(\tilde{\varvec{h}}|\tilde{\varvec{h}})^{1/2}, \end{aligned}$$
(16)

where \(\tilde{\varvec{h}}\) is the frequency-domain GW waveform of N independent detectors as mentioned in Eq. (10). The inner product is defined as

$$\begin{aligned} (\varvec{a}|\varvec{b})=2\int _{f_{\textrm{lower}}}^{f_\textrm{upper}}\{\varvec{a}(f)\varvec{b}(f)^*+\varvec{b}(f)\varvec{a}(f)^*\}\textrm{d}f, \end{aligned}$$
(17)

where \(\varvec{a}\) and \(\varvec{b}\) are column matrices of the same dimension, * represents conjugate transpose, \(f_{\textrm{lower}}\) is the lower cutoff frequency (\(f_{\textrm{lower}}=1\) Hz for ET and \(f_\textrm{lower}=5\) Hz for CE), and \(f_{\textrm{upper}}=2/(6^{3/2}2\pi M_\textrm{obs})\) is the frequency at the last stable orbit with \(M_\textrm{obs}=(m_1+m_2)(1+z)\).

2.4 Detection of short GRBs

A structured GRB jet has an angular dependence on energy and the bulk Lorentz factor, and is generally described by an ultra-relativistic core without sharp edges that smoothly transforms to a milder relativistic outflow at greater angles. Typical angular profiles are provided by Gaussian or power-law jet models. Given the uncertainty provided by one firm observation, the majority of late-time EM follow up campaigns have considered the former model [95]. According to the observations of GW170817/GRB170817A, the jet profile model of short GRB is given by [67]

$$\begin{aligned} L_{\textrm{iso}}(\theta _{\textrm{v}})=L_{\textrm{on}}\textrm{exp}\left( -\frac{\theta ^2_{\textrm{v}}}{2\theta ^2_{\textrm{c}}} \right) , \end{aligned}$$
(18)

where \(L_{\textrm{iso}}(\theta _{\textrm{v}})\) is the isotropically equivalent luminosity of short GRB observed at different viewing angles \(\theta _{\textrm{v}}\), \(L_{\textrm{on}}\) is the on-axis isotropic luminosity defined by \(L_{\textrm{on}} \equiv L_{\textrm{iso}}(0)\), and \(\theta _{\textrm{c}}\) is the characteristic angle of the core, which is given by \(\theta _{\textrm{c}}=4.7^{\circ }\). In this paper, we assume the directions of the jets are aligned with the binary orbital angular momentum, namely \(\iota =\theta _{\textrm{v}}\).

The detection probability of a short GRB is determined by \(\Phi (L)\textrm{d}L\), where \(\Phi (L)\) is the intrinsic luminosity function and L is the peak luminosity of each burst, assuming isotropic emission in the rest frame in the 1–10,000 keV energy range. In this paper, we assume an empirical broken-power-law luminosity function when considering the short GRBs

$$\begin{aligned} \Phi (L)\propto {\left\{ \begin{array}{ll} (L/L_*)^{\alpha _{\textrm{L}}}, &{} L<L_*, \\ (L/L_*)^{\beta _{\textrm{L}}}, &{} L\ge L_*, \end{array}\right. } \end{aligned}$$
(19)

where \(L_{*}\) is the characteristic luminosity separating the low and high end of the luminosity function, \(\alpha _{\textrm{L}}\) and \(\beta _{\textrm{L}}\) are the characteristic slopes describing these regimes, respectively. Following Ref. [81], we adopt \(\alpha _{\textrm{L}}=-1.95\), \(\beta _{\textrm{L}}=-3\), and \(L_{*}=2\times 10^{52}\) erg sec\(^{-1}\). Here, we term the on-axis isotropic luminosity \(L_{\textrm{on}}\) as the peak luminosity L. We also assume a standard low end cutoff in luminosity of \(L_{\textrm{min}} = 10^{49}\) erg sec\(^{-1}\).

To determine the detection probability of a short GRB by Eq. (19), we need to convert the flux limit of the GRB satellite \(P_{\textrm{T}}\) to the isotropically equivalent luminosity \(L_{\textrm{iso}}\). For the 3G GW detectors, we assume here that the future THESEUS-like telescope with its X-\(\gamma \) ray Imaging Spectrometer (XGIS) can make a coincident detection. A GRB detection is recorded if the value of the observed flux is greater than the flux limit \(P_{\textrm{T}}=0.2~\mathrm {ph~s^{-1}~cm^{-2}}\), in the 50–300 keV band for THESEUS telescope [71]. We use the standard flux–luminosity relation with two corrections: an energy normalization

$$\begin{aligned} C_{\textrm{det}}=\frac{\int ^{10{,}000~\textrm{keV}}_{1~\textrm{keV}}EN(E)\textrm{d}E}{\int ^{E_{\textrm{max}}}_{E_{\textrm{min}}}N(E)\textrm{d}E}, \end{aligned}$$
(20)

and a k-correction

$$\begin{aligned} k(z)=\frac{\int ^{E_{\textrm{max}}}_{E_{\textrm{min}}}N(E)\textrm{d}E}{\int ^{E_{\textrm{max}}(1+z)}_{E_{\textrm{min}}(1+z)}N(E)\textrm{d}E}, \end{aligned}$$
(21)

where \([E_{\textrm{min}},E_{\textrm{max}}]\) is the detector’s energy window [67, 81]. The observed photon flux is scaled by \(C_{\textrm{det}}\) to account for the missing fraction of the \(\gamma \)-ray energy seen in the detector band. The cosmological k-correction is due to the redshifted photon energy when traveling from source to detector. N(E) is the observed GRB photon spectrum in units of \(\mathrm {ph~s^{-1}~keV^{-1}~cm^{-2}}\). For short GRB, the function N(E) is simulated by the Band function [96] which is a function of spectral indices \((\alpha _{\textrm{B}}, \beta _{\textrm{B}})\) and break energy \(E_{\textrm{b}}\),

$$\begin{aligned} N(E)={\left\{ \begin{array}{ll} N_0\left( \frac{E}{100~\mathrm keV}\right) ^{\alpha _\textrm{B}}\exp \left( -\frac{E}{E_0}\right) ,&{}E\le E_{\textrm{b}}, \\ \\ N_0\left( \frac{E_{\textrm{b}}}{100~\mathrm keV}\right) ^{\alpha _\textrm{B}-\beta _{\textrm{B}}}\exp (\beta _{\textrm{B}}-\alpha _{\textrm{B}}) \\ \quad \left( \frac{E}{100~\mathrm keV}\right) ^{\beta _{\textrm{B}}},&{}E>E_{\textrm{b}}, \end{array}\right. } \end{aligned}$$
(22)

here \(E_{\textrm{b}}=(\alpha _{\textrm{B}}-\beta _{\textrm{B}})E_0\) and \(E_\textrm{p}=(\alpha _{\textrm{B}}+2)E_0\). From Ref. [81], we adopt \(\alpha _{\textrm{B}}=-0.5\), \(\beta _{\textrm{B}}=-2.25\), and a peak energy \(E_{\textrm{p}}=800~\mathrm keV\) in the source frame. This is a phenomenological fit to the observed spectra of GRB prompt emissions. According to the relation between flux and luminosity for GRB [97, 98], we can convert the flux limit \(P_{\textrm{T}}\) to the luminosity by

$$\begin{aligned} L_{\textrm{iso}}=4\pi d_{\textrm{L}}^2(z)k(z)C_{\textrm{det}}/(1+z)P_{\textrm{T}}. \end{aligned}$$
(23)

Then, the value of the on-axis luminosity \(L_{\textrm{on}}\) can be given by Eq. (18). Finally, using Eq. (19), we can select the GRB detection from the BNS samples by sampling \(\Phi (L)\textrm{d}L\).

2.5 Fisher information matrix and error analysis

The Fisher information matrix of a GW detector network is given by

$$\begin{aligned} F_{ij}=\left( \frac{\partial \tilde{\varvec{h}}}{\partial \theta _i}\Bigg |\frac{\partial \tilde{\varvec{h}}}{\partial \theta _j}\right) , \end{aligned}$$
(24)

where \(\varvec{\theta }\) denotes nine GW source parameters (\(d_\textrm{L}\), \(\mathcal {M}_{\textrm{chirp}}\), \(\eta \), \(\theta \), \(\phi \), \(\iota \), \(t_{\textrm{c}}\), \(\psi _{\textrm{c}}\), \(\psi \)) for a GW event. The covariance matrix is equal to the inverse of the Fisher matrix, i.e., \(\textrm{Cov}_{ij}=(F^{-1})_{ij}\). Thus, the instrumental error of GW parameter \(\theta _i\) is \(\Delta \theta _i=\sqrt{\textrm{Cov}_{ii}}\).

For the cosmological parameter estimations, we treat the detectable GW events belonging to the GW-GRB joint observations as standard sirens for the cosmological analysis since the redshifts can be measured by the follow-up afterglow observations under the accurate location of associated GRBs. Although the Fisher information matrix can also be used for estimating cosmological parameters, in this paper we employ the Markov-chain Monte Carlo analysis for ease of combining with the actual CMB + BAO + SN (CBS) data, which is commonly used in the literature [30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50]. We maximize the likelihood \(\mathcal {L}\propto (-\chi ^2/2)\) and infer the posterior probability distributions of cosmological parameters \(\vec {\Omega }\). The \(\chi ^2\) function is defined as

$$\begin{aligned} \chi ^2=\sum \limits _{i=1}^{N}\left[ \frac{{d}_{\textrm{L}}^i-d_\textrm{L}({z}_i;\vec {\Omega })}{{\sigma }_{d_{\textrm{L}}}^i}\right] ^2, \end{aligned}$$
(25)

where \({z}_i\), \({d}_{\textrm{L}}^i\), and \({\sigma }_{d_{\textrm{L}}}^i\) are the i-th GW event’s redshift, luminosity distance, and the total error of the luminosity distance, respectively.

For the total error of the luminosity distance \(d_{\textrm{L}}\), we consider the instrumental error \(\sigma _{d_{\textrm{L}}}^{\textrm{inst}}\) estimated by the Fisher information matrix, the weak-lensing error \(\sigma _{d_{\textrm{L}}}^{\textrm{lens}}\), and the peculiar velocity error \(\sigma _{d_{\textrm{L}}}^{\textrm{pv}}\) [39,40,41,42,43]. The total error of \(d_{\textrm{L}}\) is

$$\begin{aligned} \left( \sigma _{d_{\textrm{L}}}\right) ^{2}=\left( \sigma _{d_{\textrm{L}}}^{\textrm{inst}}\right) ^{2} +\left( \sigma _{d_{\textrm{L}}}^{\text{ lens } }\right) ^{2}+\left( \sigma _{d_{\textrm{L}}}^{\text{ pv } }\right) ^{2}. \end{aligned}$$
(26)

The error caused by weak lensing is given in Refs. [99,100,101],

$$\begin{aligned} \sigma _{d_{\textrm{L}}}^\textrm{lens}(z)=&\left[ 1-\frac{0.3}{\pi /2} \arctan (z/0.073)\right] \times d_{\textrm{L}}(z)\nonumber \\ {}&\times 0.066\left[ \frac{1-(1+z)^{-0.25}}{0.25}\right] ^{1.8}. \end{aligned}$$
(27)

The error caused by the peculiar velocity of the GW source is adopted from Ref. [102]

$$\begin{aligned} \sigma _{d_{\textrm{L}}}^\textrm{pv}(z)=d_{\textrm{L}}(z)\times \left[ 1+ \frac{c(1+z)^2}{H(z)d_{\textrm{L}}(z)}\right] \frac{\sqrt{\langle v^2\rangle }}{c}, \end{aligned}$$
(28)

where H(z) is the Hubble parameter and c is the speed of light in vacuum. \(\sqrt{\langle v^2\rangle }\) is the peculiar velocity of the GW source and we roughly set \(\sqrt{\langle v^2\rangle }=500\ \mathrm{km\ s^{-1}}\), in agreement with the average value of the galaxy catalogs [120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141]. Moreover, the synergies between GW and other cosmological probes are also discussed in Refs. [40, 41]. A comprehensive discussion of these aspects will be made in our future works.

Fig. 10
figure 10

Constraints on the \(\Lambda \)CDM model in the optimistic scenario. Left panel: two-dimensional marginalized contours (68.3% and 95.4% confidence level) in the \(\Omega _\textrm{m}\)–\(H_0\) plane using the mock standard siren data of ET, CE, 2CE, and ET2CE. Right panel: two-dimensional marginalized contours (68.3% and 95.4% confidence level) in the \(\Omega _{\textrm{m}}\)–\(H_0\) plane using the ET2CE, CBS, and CBS + ET2CE data

Full size image
Fig. 11
figure 11

Two-dimensional marginalized contours (68.3% and 95.4% confidence level) in the w–\(H_0\) and \(w_0\)–\(w_a\) planes using the ET2CE, CBS, and CBS + ET2CE data in the optimistic scenario

Full size image
Fig. 12
figure 12

Two-dimensional marginalized contours (68.3% and 95.4% confidence level) in the \(\beta \)–\(H_0\) and \(\beta \)–w planes using the CBS and CBS + ET2CE data in the optimistic scenario

Full size image
Fig. 13
figure 13

Constraints on the \(\Lambda \)CDM model in the realistic and optimistic scenarios. Left panel: two-dimensional marginalized contours (68.3% and 95.4% confidence level) in the \(\Omega _{\textrm{m}}\)–\(H_0\) plane using the realistic and optimistic scenarios of the ET2CE data. Right panel: two-dimensional marginalized contours (68.3% and 95.4% confidence level) in the \(\Omega _{\textrm{m}}\)–\(H_0\) plane using the CBS + ET2CE (realistic) and CBS + ET2CE (optimistic) data

Full size image
Fig. 14
figure 14

Two-dimensional marginalized contours (68.3% and 95.4% confidence level) in the w–\(H_0\), \(w_0\)–\(w_a\), \(\beta \)–\(H_0\), and \(\beta \)–w planes using the CBS + ET2CE (realistic) and CBS + ET2CE (optimistic) data

Full size image

5.3 Comparison with previous works

Compared to previous works [33,34,35,36,37,38,39,40,41], our main differences in this paper are as follows.

Previous works roughly assume 1000 standard sirens with detectable EM counterparts for ET or CE alone in a 10-year observation. Such treatment is optimistic and may not be realistic. In fact, in the case of a single ET with the optimistic estimate, we have only about 370 detectable GW-GRB events. Even in the case of the ET2CE network, the number of detectable GW-GRB events is about 620 in the present work. It is seen that the number of standard sirens has been significantly overestimated in the previous works. In Ref. [48], they estimated about 400 standard sirens for a single ET in a 10-year observation, which gave a slightly higher number of standard sirens. The prime cause is that we adopt the SNR threshold to be 12, while Hou et al. [48] adopt the SNR threshold to be 8.

Previous works roughly assumed that the estimated standard sirens directly followed the distribution in redshift determined by the star formation rate with long tails at larger redshift. However, in the joint GW-GRB observations, we cannot ignore the influence of the detection rate of GW detectors and GRB detectors for the events with redshifts. This leads to a lower redshift distribution, mainly at \(z\in [0,2]\) in Figs. 5 and 6, instead of the range of \(z\in [0,5]\).

Compared to previous works, it could be surprising that for a single GW detector, our constraint results of \(H_0\) are tighter. The main reason is that the redshift distributions of the standard sirens are lower, as mentioned above.

In Ref. [48], the authors focused only on the synergy of ET alone, with the THESEUS mission in the optimistic scenario for the GW-GRB detection in the IDE models. However, we make a comprehensive analysis of four different cases of 3G GW observations, single ET, single CE, the 2CE network, and the ET2CE network. Moreover, in this paper, we use the Fisher information matrix to estimate the instrumental error of the luminosity distance instead of using the approximation \(2d_{\textrm{L}}/\rho \). In addition, we also consider the realistic scenario for the GW-GRB detection. For the IDE models, we employ the ePPF method to avoid the cosmological perturbations. Compared to Ref. [48], with the above improvements, we are strongly convinced that our results will better show the potential of the cosmological parameter estimations using the 3G-era standard sirens.

5.4 Impact of the mass distributions of NSs on cosmological analysis

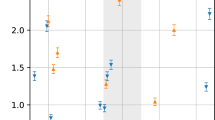
In this subsection, we investigate the impact of the mass distributions of NSs on cosmological analysis. Here we choose four typical mass distributions of NSs, i.e., the Galactic BNS mass distribution [86], the Galactic NS mass distribution [142], the POWER population model [65], and the PEAK population model [65], to perform cosmological analysis. For the mass distribution of the latter three types of NSs, we employ the numerical fitting formulas to fit the curves shown in Fig. 7 of Ref. [65]. Note that the following discussions are based on the \(\Lambda \)CDM model using ET and ET2CE in the optimistic scenario.

Fig. 15
figure 15

Distributions of \(\Delta d_{\textrm{L}}/d_{\textrm{L}}\) with respect to the redshifts for GW standard sirens using four mass distributions of NSs in the optimistic scenario. The upper panel shows the results of ET and the lower panel shows those of ET2CE. In each panel, the blue, purple, green, and orange dots and histograms indicate the Galactic BNS mass distribution, the Galactic NS mass distribution, the POWER population model, and the PEAK population model, respectively

Full size image
Fig. 16
figure 16

Constraints on the \(\Lambda \)CDM model using four mass distributions of NSs in the optimistic scenario. Upper panel: two-dimensional marginalized contours (68.3% and 95.4% confidence level) in the \(\Omega _{\textrm{m}}\)–\(H_0\) plane using the ET data. Lower panel: two-dimensional marginalized contours (68.3% and 95.4% confidence level) in the \(\Omega _{\textrm{m}}\)–\(H_0\) plane using the ET2CE data

Full size image
Table 8 The absolute (1\(\sigma \)) and relative errors of the cosmological parameters in the \(\Lambda \)CDM model using four typical mass distributions of NSs of ET and ET2CE data in the optimistic scenario for the FOV
Full size table

In Fig. 15, we show the distributions of luminosity distance uncertainty \(\Delta d_{\textrm{L}}/d_{\textrm{L}}\) with respective to the redshifts for GW standard sirens using four mass distributions of NSs. We find that \(\Delta d_{\textrm{L}}/d_{\textrm{L}}\) and redshift distributions exhibit only slight differences across the four NS mass distributions. In Fig. 16, we show the constraint results in the \(\Omega _{\textrm{m}}\)–\(H_0\) plane for the \(\Lambda \)CDM model using four mass distributions of NSs of ET and ET2CE. The detailed results are given in Table 8. We can see that the four NS mass distributions give similar constraint results, although the constraint results of the Galactic BNS mass distribution are slightly worse than those of the other NS mass distributions (the errors given by the Galactic BNS mass distribution are slightly higher than those of the other NS mass distributions). This means that the mass distributions of NSs have less impact on the cosmological analysis.

5.5 Comparison of the number of standard sirens and GW detection strategies

The impact of GWs on cosmological parameter constraints primarily arises from the number of standard sirens and the error of luminosity distance. For the same source, the errors measured by different GW detection strategies are different. In this subsection, we briefly discuss the impact of these two factors on cosmological analysis. Note that the following discussions are based on the \(\Lambda \)CDM model.

Fig. 17
figure 17

Two-dimensional marginalized contours (68.3% and 95.4% confidence level) in the \(\Omega _{\textrm{m}}\)–\(H_0\) plane for the \(\Lambda \)CDM model using 100, 300 and 500 standard sirens of ET, respectively

Full size image
Table 9 The absolute (1\(\sigma \)) and relative errors of the cosmological parameters in the \(\Lambda \)CDM model using 100, 300 and 500 standard sirens of ET, respectively
Full size table
Fig. 18
figure 18

The absolute (1\(\sigma \)) errors of the cosmological parameters in the \(\Lambda \)CDM model using different numbers of standard sirens of ET. The upper panel shows the results of \(H_0\) and the lower panel shows those of \(\Omega _{\textrm{m}}\)

Full size image

We consider a specific case of ET as a concrete example to analyze the impact of the number of standard sirens. In Fig. 17, we show the constraint results in the \(\Omega _{\textrm{m}}\)–\(H_0\) plane for the \(\Lambda \)CDM model using 100, 300 and 500 standard sirens of ET, whose redshift distributions are proportional to those in Fig. 5. The detailed results are given in Table 9. As can be seen, ET with 100 standard sirens gives the worst constraint results. Concretely, the constraint precision of the parameters \(\Omega _{\textrm{m}}\) and \(H_0\) from 300 standard sirens can be improved by 41.7% and 26.3% over those from 100. Conversely, the constraint results from 500 standard sirens are slightly better than those of 300. To further analyze the impact of the number of standard sirens on cosmological analysis, we increased the number of standard sirens used to constrain cosmological parameters, although this prediction is overly optimistic. The results are shown in Fig. 18. These results show that the number of standard sirens has an important effect on cosmological estimations, but once standard siren count reaches a certain level, further improvement in cosmological parameters becomes insignificant.

Fig. 19
figure 19

Two-dimensional marginalized contours (68.3% and 95.4% confidence level) in the \(\Omega _{\textrm{m}}\)–\(H_0\) plane for the \(\Lambda \)CDM model using 300 standard sirens of ET, CE, 2CE, and ET2CE, respectively

Full size image
Table 10 The absolute (1\(\sigma \)) and relative errors of the cosmological parameters in the \(\Lambda \)CDM model using 300 standard sirens of ET, CE, 2CE, and ET2CE, respectively
Full size table

In Fig. 19, we show the constraint results in the \(\Omega _{\textrm{m}}\)–\(H_0\) plane for the \(\Lambda \)CDM model using 300 standard sirens of ET, CE, 2CE, and ET2CE, whose redshift distributions are proportional to those in Fig. 5. The detailed results are shown in Table 10. We can see that ET gives the worst constraint results. Compared with ET, the constraint precision of the parameters \(\Omega _{\textrm{m}}\) and \(H_0\) from CE can be improved by 36.4% and 57.9%. Conversely, the 2CE and ET2CE’s constraint capabilities on the cosmological parameters are slightly better than those of CE. Therefore, with the same number of standard sirens, different GW detection strategies have significant impacts on cosmological analysis. CE, 2CE, and ET2CE give similar constraint results, which are much better than those of ET.

6 Conclusion

In this work, we show the potential of the GW standard sirens from the 3G GW detectors in constraining cosmological parameters. We explore the synergy between 3G GW detectors and GRB detector THESEUS-like telescope for the multi-messenger observations. We consider four GW observation strategies, i.e., ET, CE, the 2CE network, and the ET2CE network. Five cosmological models, \(\Lambda \)CDM, wCDM, \(w_0w_a\)CDM, I\(\Lambda \)CDM, and IwCDM, are considered to perform cosmological analysis. Moreover, we consider the optimistic (assuming all the detected short GRBs could determine redshifts) and realistic (assuming 1/3 of the detected short GRBs could determine redshifts) cases for FOV to make the multi-messenger analysis.

We first predict the expected detection rates of the GW-GRB events based on the optimistic and realistic cases. For the detector network, the expected number of GW-GRB is almost double compared to the single ET observatory. About \(\mathcal {O}(100)\) GW-GRB events could be detected based on the 10-year observation. Moreover, the detected GW-GRB events have \(z<3.5\) and \(\iota <15^\circ \).

We find that GW gives quite tight constraints on the Hubble constant, with precision from 0.345% to 0.065%. However, GW gives loose constraints on the other cosmological parameters in both optimistic and realistic scenarios. Fortunately, since GW has an advantage in measuring the absolute luminosity distance, GW can break the cosmological parameter degeneracies generated by other EM observations, thus improving the measurement precision of cosmological parameters. When combining CBS with ET2CE, the constraint precision of the EoS parameter of dark energy w can reach 1.26%, which is close to the standard of precision cosmology. With the addition of ET2CE to CBS, the constraints on cosmological parameters can be improved by 34.2–94.9%. We can conclude that (i) the synergy between 3G GW detectors and THESEUS could detect \(\mathcal {O}(100)\) multi-messenger events based on the 10-year observation; (ii) GW can provide rather precise measurement on the Hubble constant with a precision of 0.065%, but can be poor at measuring the other cosmological parameters; (iii) GW can significantly break the cosmological parameter degeneracies generated by the other EM observations and the combination of them is expected to precisely measure dark energy. It is worth expecting that GW standard sirens from the 3G GW detectors can help make arbitration for the Hubble tension and explore the fundamental nature of dark energy.