INTRODUCTION

Active tectonic processes in the Eastern Mediterranean are due to the interaction between the African and the Arabian lithospheric plates and the Anatolian Block (McClusky et al., 2000; Ergin et al., 2004; Reilinger et al., 2006, etc.). Moving towards the Eurasian Plate, the African and the Arabian plates are pushing westwards the Anatolian Block that is moving along two major strike-slip faults: the right lateral North Anatolian Fault and the left lateral East Anatolian Fault (Milkereit et al., 2004). As the Arabian Plate is moving faster than the African Plate (18–25  and around 10 mm/year, respectively), the Anatolian Block is rotating counterclockwise (McClusky et al., 2000; Reilinger et al., 2006; Xu et al., 2020).

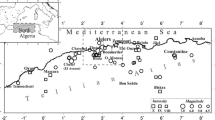
The boundary between the Anatolian Block and the Arabian Plate is on the East Anatolian Fault Zone (hereinafter, the EAFZ), one of the largest intracontinental transform zones of the Eastern Mediterranean (Fig. 1). In the north, the EAFZ merges with the North Anatolian Fault near Karlıova. A wide system of faults is distinguished within the EAFZ. For convenience, in what follows we conditionally divided the EAFZ into three segments, of which the northern segment extends from Karlıova to Çelikhan. Near Çelikhan, a system of Sürgü–Çardak faults extends west of the EAFZ, its continuation gradually turns south-west to join the Kyrenia (Κερύνεια) Fault Zone in the Gulf of Iskenderun (Duman and Emre, 2013).

Fig. 1.
figure 1

The region of the catastrophic earthquakes in Turkey of February 6, 2023 (the epicenters are marked with stars). Black lines—the active faults system according to the database of the Geological Institute of the Russian Academy of Sciences (GIN RAS) (http://neotec.ginras.ru/database.html). Red lines show the faults discussed in the paper. Rectangular areas—the contours of the satellite images covering the earthquake epicenters (in blue—the descending orbit, in green—the ascending one). The background map is ESRI (Environmental System Research Institute) Shadow Relief. The East Anatolian Fault segments marked with arrows: The southern EAFZ segment (Antakya-Türkoğlu), the central EAFZ segment (Türkoğlu–Çelikhan), the northern EAFZ segment (Çelikhan–Karlıova). The rectangular box on the insert in the top left-hand corner shows the location of the study region on the map of the Eastern Mediterranean.

Full size image

The central segment of the EAFZ extends from Çelikhan toward Türkoğlu. The southern segment from Türkoğlu to Antakya coincides with the Karasu fault zone, which in the south links to the Cyprus arc. East of the Karasu zone, there is the South Hatay Fault Zone, which in the south connects with the Dead Sea Fault Zone (Özmen et al., 2017). Between these fault zones is the Karasu rift zone, 150 km long and ~25 km wide (Özmen et al., 2017).

In the last one hundred years, along the EAFZ there have been series of earthquakes, most of them of magnitude 3.5–6.4; in the last decades no significant seismic activity above the magnitude 6.7 has been observed in the zone (Bayrak et al., 2015; Xu et al., 2020). Among the latest events, let us note three earthquakes that occurred near Sivrice, Elazığ Province. Those were the Mw 6.7 Doğanyol–Sivrice earthquake of January 24, 2020, and two closely-spaced Mw 5.6 and 5.5 events of August 4, 2020 and December 27, 2020 (according to the United Stated Geological Survey,Footnote 1 USGS). The earthquakes occurred in that part of the EAFZ, where the rupture area during the main event Mw 7.8 of February 6, 2023 extended along that fault.

The series of the catastrophic Kahramanmaraş earthquakes of February 6, 2023 started at 01:17:34 (UTC) from the Pazarcik event Mw 7.8 (USGS), which, 11 min later, was followed by an aftershock of magnitude 6.7. The earthquake hypocenter was at the depth of 17.5 km, at 37.225° N, 37.021° E, 35 km west of Gaziantep. The epicenter was determined on a small fault, in the northern continuation of the East Hatay Fault Zone (Fig. 1). According to USGS, the fracture was moving northwards, in the direction of the EAFZ, and triggered a rupture that extended north-east and south-west along the EAFZ for over 100 km in each direction.

Nine hours later, at 10:24:49 (UTC), the second large Mw 7.5 earthquake occurred 90 km to the north, on the Sürgü–Çardak fault (Basili et al., 2013). The hypocenter was determined at the depth of 13.5 km, at 38.024° N, 37.203° E. Those earthquakes triggered numerous aftershocks along the entire EAFZ and were the most damaging in the history of the country (see data according to the Disaster and Emergency Management Authority (AFAD) of TurkeyFootnote 2). The most severe damages from the first earthquake were seen in Kahramanmaraş and Hatay Provinces; the highest damage from the second earthquake was in Malatya Province. The earthquakes caused surface ruptures and fractures, with prevailing left lateral strike-slip displacements.

According to AFAD, as a result of the first earthquake the surface rupture extended for 290 km. In the EAFZ segment north-east of Türkoğlu, the maximum strike-slip displacements were up to 5.5 m. The rupture of the second earthquake extended for 130 km. Here, the maximum displacements were up to 6 m. Afterwards, rockfalls, landslides and ground liquefaction were observed, too. Because of the wide-spread destruction and devastating collapse of residential buildings and structures, the event of February 6, 2023 was recognized to be one of the most catastrophic earthquakes since the beginning of the 21st century. It ranks fifth by the number of fatalities. According to USGS, more than 160 000 people died and were injured, 1.5 million people were made homeless, more than 164 000 buildings were destroyed.

Thanks to the satellite technologies for the remote sensing of the Earth’s surface, it was possible to quickly and efficiently examine the extensive area of the earthquakes. In this study, by using SAR interferometry methods and SAR images from the Sentinel-1A satellite we determined the Earth’s surface displacement fields, constructed a rupture surface model, and identified co-seismic displacements on it. We also studied the post-seismic displacements, specifically, in the area of the Mw 6.3 earthquake near Antakya on February 20, 2023.

METHOD

Satellite SAR interferometry allows estimating with high accuracy displacements of the Earth’s surface and infrastructure facilities for the time between two repeat-pass images (Hanssen, 2001; Massonnet and Souyris, 2008). Synthetic aperture radars (SAR) mounted on board the satellites create amplitude-phase images, in any weather condition and illumination, which makes this technology essential in monitoring natural and man-made processes. The Sentinel-1A satellite images are made at an interval of 12 days and become available in the database of the European Space Agency (ESA) several hours after imaging. Unlike ground-based methods focused on the examination of relatively small areas, SAR interferometry allows creating maps of deformation of the Earth’s surface that cover vast territories. For example, the size of an image from the Sentinel-1A satellite can be as large as 200 × 250 km. In this study, for estimating the displacement fields from satellite SAR images we used the differential interferometry (DInSAR) method and the offset method, in English-language publications also referred to as “amplitude tracking” or “sub-pixel offset techniques” (e.g., (Michel et al., 1999)).

The DInSAR method allows determining the Earth’s surface displacements by the difference of phases of the radar signal reflected from the resolution cell at two different moments of time. The phase value is fixed along the direction of the electromagnetic radiation, accordingly, the values of displacements are measured in a projection to the line of propagation of the radar signal (the line-of-sight, LOS). The images must correlate with one another in order to calculate the displacements. The correlation measure is the coherence coefficient varying from 0 to 1. The decorrelation effect, to which low coherence values correspond, arises, inter alia, due to sudden topographic changes caused by huge displacements, for example, during an earthquake. Besides, the difference of phases of reflected signals is within the range from –π to π. When calculating the displacement fields, we need to unwrap the 2π modulo-wrapped phase. The unwrap** that implies adding to the recorded phase the necessary number of full periods is an ambiguous operation, that is why it is performed under the condition that the phase should not vary more than by half a period in the neighbouring pixels. For this reason, the unwrap** is not easy in the areas of large deformations, specifically, near the point where a seismic rupture breaks through to the surface, where the displacements can extend for metres and more. In such areas, the differential interferometry method that analyses only the phase component of a SAR image does not always yield the expected result. In such cases, the offset method proves to be more effective.

The offset method is based on a cross-correlation of amplitudes of two images. After the identification of the same objects in two images, the offset between them can be measured within a pixel and split into components by two directions of the radar coordinate system: perpendicular (range) and parallel (azimuth) to the satellite motion path. Each of the considered methods (phase and amplitude) has its advantages and disadvantages. First, it is the accuracy of measurements. In DInSAR, the accuracy of displacements depends on the value of coherence and the radar wavelength. Even at conditionally low coherence γ = 0.2 and the wavelength λ = 56 mm (Sentinel-1), the accuracy of the determination of the displacement fields is in fractions of a centimetre (Ferretti, 2014). The accuracy of estimating the displacements by the offset method depends on the pixel size (or the window size) in calculations of cross-correlation by amplitudes of two images, and the signal-to-noise ratio. According to (Strozzi, 2002), the accuracy of estimates of the displacements by the slant range and azimuth is around 1/20 pixel. At the same time, the offset method eliminates the laborious and ambiguous phase unwrap** operation, is less sensitive to the effect of the atmospheric disturbances than the DInSAR method, and reveals significant displacements (up to several metres) that occur within the time interval between SAR images. This is exactly the scale of the deformations that were observed in the EAFZ segments during the earthquakes in Turkey.

RESULTS OF ESTIMATES OF DISPLACEMENTS BY SAR INTERFEROMETRY METHODS

The displacement fields were estimated using images from the Sentinel-1A satellite from the 21st descending orbit and from the 14th ascending orbit. The image boundaries are shown in Fig. 1. The fields of the co-seismic displacements were calculated based on the interferogram obtained from the two images from the descending orbit of January 29, 2023 and February 10, 2023, using the DInSAR method; the post-seismic displacements were calculated from the images of February 10, 2023 and February 22, 2023. The interferogram is highly sensitive to dissected topography and large deformations, and because of this in the areas of metre displacements in the near-fault zone there appeared image decorrelation areas where the unwrap** was impossible due to low coherence or where phase unwrap** errors occurred. The results will be shown below.

From DInSAR, the displacements are determined in the direction towards the satellite (\({{U}_{{los}}}\)) and include the vertical and the horizontal components of the displacement vector. According to AFAD, mainly strike-slip displacements occurred on the EAFZ during the earthquakes. The offset method also proves to be effective in such cases. Let us analyse the results obtained by using these methods. On the maps given below, positive displacements are displacements eastwards, northwards and towards the satellite.

DISPLACEMENTS OBTAINED BY THE OFFSET METHOD

Based on two images from the descending orbit (January 29, 2023 and February 10, 2023), maps of displacements in the range and azimuth directions were obtained using the offset method (Fig. 2a, 2b).

Fig. 2.
figure 2

Displacements of the Earth’s surface (in meters) obtained by the offset method. At the top—from the images from the descending orbit in the direction of the range (a) and azimuth (b). The figure also shows the range (red) and azimuth (blue) displacements in metres along the profiles shown with the lines on the maps. At the bottom—displacements from the images from the ascending orbit, also in the direction of the range (c) and azimuth (d). Az shows direction along the orbit, R—perpendicular to the orbit.

Full size image

If the module of the vector of the horizontal displacements at some point on the Earth’s surface equals US, then the displacements along the orbit (in azimuth)—\({{U}_{{Az}}}\) and in range—\({{U}_{R}}~\) will be:

$$\begin{gathered} {{U}_{{Az}}}\,\,~ = \,\,~{{U}_{s}}\cos \left( {\beta - {{\alpha }_{h}}} \right), \\ {{U}_{R}}~\,\, = ~\,\,{{U}_{s}}\sin \left( {\beta - {{\alpha }_{h}}} \right), \\ \end{gathered} $$
(1)

where \({{\beta }}\)—is the displacement vector azimuth \(~{{U}_{s}}\); \({{{{\alpha }}}_{h}}\)— is the orbit azimuth (angles are measured clockwise from the direction northwards). In the calculations according to the formulas (1) positive will be displacements in the direction of the orbit azimuth and away from the satellite, so, for the ascending orbit the displacements \({{U}_{{Az}}}~\) and \({{U}_{R}}\) will be positive if the reflecting object has shifted northwards and/or eastwards. For the descending orbit, such displacements will be negative. For the convenience of comparing the results obtained from different orbits, the sign of the displacements in Fig. 2 is changed so that all the displacements are positive northwards and eastwards. To this purpose, the azimuth and range displacements obtained from the descending orbit are taken with the opposite sign.

It is evident that the horizontal displacements will manifest themselves best where the vectors of the displacements and the direction of the measurements (azimuth or range) are collineral. For example, on the Sürgü-Çardak fault, in the epicentral area of the Mw 7.5 earthquake, the range displacements are quite prominent (Fig. 2a) while the azimuth-measured displacements in the same area do not exceed the noise level (Fig. 2b). In Profile 1–1' it can be seen that the maximum amplitude of the range displacements on the Sürgü-Çardak fault is more than 7 m.

In the southern section of the EAFZ from Türkoğlu to Antakya, the range displacements are significantly smaller than the real displacements, especially in the area of the Karasu rift. As the direction of the strike of the faults in this area is close to the trajectory of the descending orbit (the maximum angle of the East Hatay Fault to the orbit does not exceed 6°), the azimuth displacements in this area, shown in Fig. 2b, are closest to the real ones. In the area of Profile 2–2', the amplitude of the azimuthal offsets is more than 4 metres, and by the range it is at least half as large (Fig. 2b).

The displacements in the central segment of the EAFZ, from Türkoğlu to Çelikhan, are distinguished best of all in the direction of the range. The maximum amplitudes of the range offsets increase in this segment from 4.5 to 6 m with the movement further along the fault north-eastwards to Çelikhan (Profiles 3 and 4 in Fig. 2b). The field of the azimuth displacements in this area has a low signal-to-noise ratio.

Also, the offset method was used to obtain the range and azimuth displacements based on two images from the ascending orbit for the period from January 28, 2023 to February 9, 2023 (Fig. 2c, 2d). The imaging geometry for the ascending orbit is less matched to the fault strike, that is why the range (Fig. 2c) and azimuth (Fig. 2d) displacement fields are less discernible in the images captured from this orbit. Most distinct are the range displacements only in the central segment of the EAFZ (Fig. 2c). The displacements in this area match well with the range displacements from the descending orbit. In Fig. 2d, the desired signal is close to the noise level.

Knowing the azimuth and range displacements, we can calculate from the formulas (1) the module of the vector of the horizontal displacements and its direction (Fig. 3). These values do not depend on the imaging geometry. From Fig. 3 it follows that a large part of Eastern Turkey suffered displacements of more than 1 m. The maximum strike-slip displacements occurred on the Sürgü-Çardak fault and in the central and northern segments of the EAFZ. Here, the displacements were larger than 5 m. The arrows show the direction and the amplitude of all displacements, including landslides and rockfalls during the imaging period. In general, the arrows clearly indicate the strike-slip displacements in opposite directions on the fault sides.

Fig. 3.
figure 3

The amplitude of the displacement vectors of the Earth’s surface (the colour scale), and displacement directions (arrows). The maximum arrow corresponds to the 5.22 m displacement. The black line goes along the rupture surface. The blue and the yellow stars are the epicenters of the main earthquakes.

Full size image

DISPLACEMENT FIELDS OBTAINED BY THE DINSAR METHOD

The displacement fields in the direction towards the satellite Ulos, obtained with the DInSAR method, can be split into the vertical and the horizontal components:

$${{U}_{{los}}} = {{U}_{{up}}}\cos \left( \theta \right) - {{U}_{R}}\sin \left( \theta \right),$$
(2)

where θ—is the incidence angle (deviation of the direction of propagation of the radar signal from the vertical), \({{U}_{{up}}}\)— is the amplitude of vertical displacements, \({{U}_{R}}\)—are horizontal range displacements calculated according to the formula (1). As the earthquakes under study caused mainly horizontal displacements, then, assuming that the vertical component equals zero, we arrive at the estimate of the strike-slip range displacements:

$${{U}_{R}} \approx {{ - {{U}_{{los}}}} \mathord{\left/ {\vphantom {{ - {{U}_{{los}}}} {\sin \left( \theta \right).}}} \right. \kern-0em} {\sin \left( \theta \right).}}$$
(3)

The incidence angle θ during the imaging of the territory covered by the images from the descending orbit of January 29, 2023 and February 10, 2023 varies in the range from 30° to 46°, from the right image boundary to the left one. Since this angle is known for each reflecting pixel, the displacements \({{U}_{{los}}}\) can be re-estimated to the range displacements and matched against the results obtained by the offset method (Fig. 4). These displacements match well, except for the near-fault zones because in such zones the phase unwrap** can fail or can yield smoothed values. The greatest differences are in Profile 2–2' intersecting the Gölbaşı Basin (Westaway and Arger, 1996). Here, the area of the positive displacements in the direction towards the satellite are on either side of the EAFZ (Fig. 4), whereas on the range displacement maps (Fig. 2) the displacements change sign at the EAFZ. The differences can be due to the phase unwrap** errors, since there are two large reservoirs in the valley, whose surface has near-zero coherence. Some of the existing differences can be associated with the presence of the vertical component in the displacements, which we neglected in formula (3).

Fig. 4.
figure 4

Comparison of the range displacements (in metres), calculated using the offset method, with the displacements obtained by the DInSAR method and re-estimated to the range displacements by formula (3). In the profiles on the right, along the lines shown in red on the map: in blue—the displacements \({{U}_{R}}\) calculated from \({{U}_{{los}}}\); in red—the range displacements calculated using the offset method.

Full size image

The post-seismic displacements calculated by the DInSAR method from the two images from the descending orbit of February 10, 2023 and February 22, 2023 showed that no other significant displacements were observed in that period on the faults, except for the region of Antakya where an earthquake of magnitude 6.3 occurred on February 20, 2023, with the epicenter at 36.154° N, 36.037° E (USGS). In Fig. 5, the epicenter is denoted with a red star. The maximum displacements in the LOS direction, away from the satellite, were –16 cm (Profile 2). The epicenter is in the south-west of the area of the negative LOS displacements (“subsidence”). From the displacement field geometry it can be concluded that the displacements occurred along the nodal plane having a strike of 225° and the dip of 53° (according to USGS). The rake angle from seismic data is –27°, which corresponds to a left lateral slip with a thrust component.

Fig. 5.
figure 5

Post-seismic displacements (in metres) on the map and along the profiles shown with red lines, obtained by the DInSAR method in the LOS direction from the Sentinel-1A images of February 10, 2023 and February 22, 2023. Stars show the epicenters of the earthquakes: green stars—the earthquakes of February 6, 2023 (Mw 7.8, Mw 7.5), the red star—the earthquake of February 20, 2023 (Mw 6.3).

Full size image

In the area where the Sürgü-Çardak fault comes close to the central segment of the EAFZ, displacements with an amplitude of up to 10 cm were obtained. Here, the displacements during the earthquake were small. It is possible that at the post-seismic stage the fault slightly moved eastwards.

SEISMIC RUPTURE SURFACE MODELLING

So, from the satellite images a set of data on the displacements on the EAFZ was obtained: the azimuth and range displacement fields from the descending and ascending orbits, the field of displacements in the direction towards the satellite Ulos. In general, the fields are in good agreement. The field Ulos is reconstructed with an error where the amplitude of the displacements was several metres due to phase unwrap** problems. The displacements yielded by the offset method from the images from the ascending orbit (Figs. 2c, 2d) have a lower signal-to-noise ratio than those obtained from the descending orbit (Figs. 2a, 2b). Having a set of various data, we could construct our model selecting data with the maximum signal-to-noise ratio, namely: for the northern part of the area, above 37.4° N, we used the range displacements obtained by the offset method from the descending orbit. South of parallel 37.0° N, the azimuth displacements determined also from the descending orbit were used.

Using the faults database (Bachmanov et al., 2017) and the line that demarcates the displacements in the opposite directions on the offset map, we set a seismic fault trace on the daylight surface (the black line in Fig. 3). Then, that line was approximated by segments of the straight lines that were the upper boundary of the rectangular planes approximating the seismic rupture. The Sürgü-Çardak fault trace was divided into 4 elements along the strike, and the EAFZ—into 15 elements (Fig. 6), of which 7 elements were along its southern segment, and 8 elements were in the central and northern segments. On the Sürgü-Çardak fault, the rupture was set at a depth from 0.5 to 20 km with a northward dip at the angle of 80°; in the EAFZ, the depth of the upper edge was set equal to 1 km, of the lower edge—20 km (as in (Barbot et al., 2023)), with a north-westward dip at the angle of 85° according to (Basili et al., 2013, Bachmanov et al., 2017). The small rupture that triggered the earthquakes was approximated by one rectangular element, with the upper edge 0.5 km deep, the lower edge—15 km deep, and the dip angle of 85° eastwards. The rupture length of 15 km along the strike was determined from the displacement map (Fig. 2), according to which the rupture did not arrive at the EAFZ.

Fig. 6.
figure 6

Model of the rupture surface of the February 6, 2023 earthquakes constructed from the SAR interferometry data. A colour map shows the range displacements (in cm) of the Earth’s surface, obtained by the offset method from the images from the descending orbit. Black isolines—the same displacements provided by the model. Black rectangles indicate the rupture surface in the vertical section, with the displacements at the upper, middle and lower levels (black arrows). Light-blue arrows along the faults indicate the displacements at the upper model level on the same scale. The maximum arrow length of 10.2 m is at the upper level of the central segment of the EAFZ. Dark red lines—profiles through the rupture area. On the left, SAR data (in red) and model-based fitting (in blue) are given for those profiles. The red rectangle at the northeast end of the EAFZ shows a part of the USGS-constructed model of the January 24, 2020 earthquake.

Full size image

By the depth, the models of the main faults were divided into three levels of the equal extension along the dip. The solution was found under the regularizing condition that the displacements are close to a pure shear. Our model is based on the solution of the problem of strain on the surface of a layered spherical Earth caused by along dip and strike displacements on a rectangular fault located at a target depth (Pollitz, 1996). The procedure for solving the posed inverse problem is described in detail in (Mikhailov et al., 2010).

In the surface rupture model, presented in Fig. 6, the arrows indicate directions of the displacements on the hanging wall of the faults. For the EAFZ, we set the dip toward north-west at the angle of 85°. The results vary slightly if the dip is set toward south-east at the same angle as in the USGS model constructed from seismic data.

In the southern segment of the EAFZ, the displacements monotonically increase from south to north. In the southernmost element, the displacements in the lower part are estimated at 2.0 m, and in the upper part—at less than 0.11 m. This is where an earthquake of magnitude 6.3 (Fig. 5) will occur on February 20, 2023, with its hypocenter at the depth of 11.5 km, i.e. in the upper part of the mid-level of the model.

Further north, the displacements in the upper part of the southern segment of the seismic rupture increase to 5.8 m, in the middle part—to 2.5 m, and in the lower part—to 1.5 m maximum.

In the central segment of the EAFZ, where its strike turns to the north-northeast, the displacements on the seismic rupture increase significantly. In some elements of the rupture surface the displacements exceed 10.2 m. In the northern segment, the displacements decrease, but still, on the lower level of the northernmost section they equal 3.4 m. The southern end of the model of the seismic rupture of the Mw 6.7 Doğanyol–Sivrice earthquake of January 24, 2020, published on the USGS Website (the red rectangle in Fig. 6), overlaps with the third-from-the-north element of our model, where the upper level displacements are 6.8 m.

In three eastern segments of the seismic rupture along the Sürgü–Çardak fault, pure strike-slip displacements occurred, and in its western element also a thrust component was observed, where the rupture turns southwards (Fig. 6). The displacements in the upper part of the rupture increase from east to west. At the lower levels of the rupture, more intense displacements occurred in the east.

The displacements on the small fault, where the seismic events of February 6, 2023 began, are estimated at 2.1 m.

DISCUSSION AND CONCLUSIONS

A detailed analysis of the satellite SAR images yielded horizontal displacements along the EAFZ and Sürgü–Çardak faults, as well as a small fault on the extension of the East Hatay Fault Zone, where a series of catastrophic earthquakes began. The most discernible displacements were obtained by the offset method using images from the descending orbit. The displacements on the Sürgü–Çardak fault and also in the central segment, from Kahramanmaraş (the Mw 7.8 epicentral area) north-east to Çelikhan, and in the northern segment of the EAFZ, are distinguished best of all in the range direction (Fig. 2a). Along the southern segment of the EAFZ, striking south-southwest from the epicenter of the main Mw 7.8 event to the coast, the most distinct are the azimuth displacements (Fig. 2b). From the available dataset, for constructing the model the data with the maximum signal-to-noise ratio were selected: for the northern part of the area, above 37.4° N—the range displacements obtained by the offset method from the descending orbit, and south of parallel 37.0° N—the azimuth displacements from the same descending orbit.

The model was constructed using the solution of (Pollitz, 1996) made for the spherical, radially layered Earth model. The mentioned study demonstrated that ignoring the radial layering of the planet leads to errors up to 20%, with the largest errors occurring in the presence of a large strike-slip component. Ignoring sphericity also introduces an error when using the solution in the framework of the idealization of an elastic homogeneous half-space (Okada, 1985) which was used when constructing USGS and (Barbot et al., 2023) models.

As distinct from the USGS model, our model offers a more detailed geometry of the seismic rupture surface. We approximated the rupture by 19 rectangular elements along the strike, divided into three levels along the dip. According to our model, the strike-slip displacements in the central segment of the seismic rupture along the EAFZ are up to 10.2 m. In the southern segment of the rupture, the displacements are much smaller. It should be emphasized that the displacements of the Earth’s surface were recorded by us for the time period from January 29, 2023 to February 10, 2023, i.e. they include also the post-seismic displacements for 4 days after the main seismic events.

In our model, just as in the rupture surface model published on the USGS Website and in (Barbot et al., 2023), in the southern segment of the EAFZ the displacements increase from south to north and are concentrated mainly in the upper part of the Earth’s crust to a depth of 10 km. At the southern end of that section of the rupture, where an earthquake of magnitude 6.3 occurred on February 20, 2023 with the hypocenter depth of 11.5 km, at the lower levels of our model the obtained displacements are up to 2 m, and almost no displacements are observed at the upper level (11 cm).

The area of the most intense displacements on the EAFZ is in its central segment. Here, in all models the displacements go into depth, and in our model they are as big as 10.2 m, which is in agreement with (Barbot et al., 2023) and with the USGS model (11 m).

Let us note than the northern end of the obtained rupture on the EAFZ overlaps with the southern end of the rupture surface model of the January 24, 2020 Doğanyol-Sivrice earthquake of Mw 6.7, published on the USGS Website. The southern end of the USGS model is within the third-from-the-north element of our model, where the lower level displacements are 5.3 m, the mid-level ones—3.3 m, and the upper level ones—6.5 m. In the (Barbot et al., 2023) model, the displacements in this area are not that big, which let the authors conclude that there is a seismic gap here and there is a risk of a new earthquake. Our data do not confirm this conclusion because exactly at the southern end of the rupture surface of the January 24, 2020 Doğanyol-Sivrice earthquake the displacements in our model increase sharply.

In all models, significant displacements on the Sürgü–Çardak fault are obtained at a depth of up to 20 km. In the USGS model, the amplitude of the displacements exceeds 11 m; in our model, in the upper part of the westernmost element they are 9.8 m; in the (Barbot et al., 2023) model, the displacements here are slightly smaller.

On the whole, our results accord with (Barbot et al., 2023), except for the presence of a seismic gap. One of the reasons for the discordance can be the difference in the solution methods. We use the regularizing condition of the proximity of the rake angle in the model to the seismic source mechanism (Mikhailov et al., 2019; Diament et al., 2020). Other authors use the condition of smoothness of the obtained displacement field.

The obtained results once again prove the effectiveness of using satellite SAR interferometry in the study of geodynamic processes.