Multi-dimensional classification: paradigm, algorithms and beyond

Abstract

Multi-dimensional classification (MDC) aims at learning from objects where each of them is represented by a single instance while associated with multiple class variables. In recent years, this practical learning paradigm has attracted increasing attentions in machine learning community. In this paper, a timely review on this topic is provided with emphasis on representative algorithms. Firstly, the MDC learning framework, commonly used evaluation metrics and publicly available MDC datasets are given. Then, eight state-of-the-art MDC algorithms are scrutinized as the representatives of three categories. After that, several related learning settings are briefly summarized. Finally, this paper is concluded with discussing some open problems to be studied in the future.

1 Introduction

Machine learning is an important approach to artificial intelligence (AI) [1, 2], where supervised learning is one of the mostly-studied and widely-used learning paradigms that has played a crucial role in the advancement of AI capabilities. In traditional supervised learning, each object is represented by a single instance to characterize its properties in feature space, and associated with a single label to characterize its semantics in output space. Specifically, let $\mathcal {X}$ and $\mathcal {Y}$ be the feature space and output space respectively, the traditional supervised learning aims to learn a map** function f from $\mathcal {X}$ to $\mathcal {Y}$ based on a training set $\mathcal {D} = \{(\varvec{x}_i, y_i) \mid 1 \le i \le m \}$, where $\varvec{x}_i \in \mathcal {X}$ denotes the i-th instance and $y_i \in \mathcal {Y}$ denotes its corresponding label.

In traditional supervised learning (e.g., multi-class classification), it is worth noting that the output space usually characterizes the semantics of objects with a single label along one dimension. However, for many real-world applications where objects have rich semantic information, it is not enough to describe the semantics of objects from a single dimension. For example, in music categorization, it is usually needed to classify a piece of song from the emotion dimension (with possible classes happy, sad, relax, etc.), from the genre dimension (with possible classes popular, classical, rock, etc.), and from the scenario dimension (with possible classes wedding, memorial, saloon, etc.). Such kinds of applications widely exist in computer vision [3,4,5,6,7,8,9], text mining [10,11,12,13,14], bioinformatics [15,16,17,18,19,20,21], ecology [22, 23], and beyond [24,25,26,27,28,29,30,31,32,33].

To model the rich multi-dimensional semantics of objects, one direct solution is to utilize multiple class variables in output space to explicitly express their semantics from multiple dimensions. Under this consideration, the paradigm of multi-dimensional classification (MDC) naturally arises. In contrast to traditional supervised learning, each MDC object is also represented by a single instance in feature space while associated with multiple class variables in output space. Here, each class variable corresponds to one class space, which characterizes the semantics of objects from one dimension¹. In other words, the labeling information of one MDC object is represented by a class vector instead of a single label, where each item in class vector denotes the semantics of object in one different dimension. The task of MDC is to learn a map** function which can return a proper class vector for unseen instance.

Early MDC researches mainly focus on solving MDC problem via Bayesian techniques [34,35,36,37,38,39,40,41,42,43,44,45,46,47,48] which have been reviewed [49]. In recent years, especially during the past five years, more and more attentions have been attracted from machine learning community and many MDC algorithms based on non-Bayesian techniques are proposed. In this paper, a timely review on this emerging area is provided, where we organize the state-of-the-art works in three parts. In the first part (Section 2), we aim to present the fundamentals related to MDC, including the formal definitions of the learning framework and the evaluation metrics, and the publicly available MDC datasets. In the second part (Section 3), we aim to present the technical details of some representative MDC algorithms which forms the main body of the paper. In the third part (Section 4), we aim to present several learning settings related to MDC. Finally, this paper is concluded in the last section with discussing open problems that need to be further studied in the future.

2 The paradigm

Notation. In this paper, we use $\{ \cdots \}$ to denote a set and $[ \cdots ]$ to denote a vector or a matrix. A matrix is denoted by one capital bold letter (e.g., $\textbf{X}$) and a (column) vector is denoted by one lowercase italic bold letter (e.g., $\varvec{x}$). Superscript $^{\textrm{T}}$ denotes the transpose of one matrix or vector (e.g., $\textbf{X}^{\textrm{T}}$ and ${\varvec{x}}^{\textrm{T}}$ ). For matrix or vector, comma denotes row concatenation and semicolon denotes column concatenation, e.g., both ${\varvec{x}} = [x_1, x_2, x_3]^{\textrm{T}}$ and ${\varvec{y}} = [y_1; y_2; y_3]$ are length-3 column vectors, $\textbf{A} = [{\varvec{x}}, {\varvec{y}}]$ is a $3 \times 2$ matrix and $\textbf{B} = [{\varvec{x}}^{\textrm{T}}; {\varvec{y}}^{\textrm{T}}]$ is a $2 \times 3$ matrix.

2.1 Learning framework

Let $\mathcal {X}$ denote the d-dimensional input (feature) space, and $\mathcal {Y}=C_1 \times C_2 \times \cdots \times C_q$ denote the output space which corresponds to the Cartesian product of q class spaces. Here, $C_j$ denotes the j-th class space which contains $K_j$ class labels ($1\le j\le q$), i.e., $C_j=\left\{c^j_1,c^j_2,\ldots ,c^j_{K_j}\right\}$. Given a set of MDC examples $\mathcal {D}=\{({\varvec{x}}_i,{\varvec{y}}_i)\mid 1\le i\le m\}$, for each example $({\varvec{x}}_i,{\varvec{y}}_i)\in \mathcal {D}$, ${\varvec{x}}_i = [x_{i1},x_{i2},\ldots ,x_{id}]^{\textrm{T}} \in \mathcal {X}$ is a d-dimensional feature vector and ${\varvec{y}}_i = [y_{i1},y_{i2},\ldots ,y_{iq}]^{\textrm{T}} \in \mathcal {Y}$ is the q-dimensional class vector associated with ${\varvec{x}}_i$. In ${\varvec{y}}_i$, the j-th item $y_{ij}$ must take one possible class label in $C_j$, i.e., $y_{ij} \in C_j$. The learning task of MDC is to train a predictive model $f:\mathcal {X}\mapsto \mathcal {Y}$ from $\mathcal {D}$ which can return a proper class vector $f({\varvec{x}_*}) \in \mathcal {Y}$ for unseen instance ${\varvec{x}_*}$. To facilitate understanding, the notations are further summarized in Table 1.

Table 1 Notations in the MDC setting

Fig. 1

A toy example for multi-dimensional classification. a Classification via shape (square, circle and triangle); b Classification via color (white, grey and black); c Classification via size (big, small and medium)

Figure 1 presents a toy MDC example to give an intuition. It is easy to know that, there are three class spaces (i.e., $q = 3$) and each contains three class labels (i.e., $K_1 = K_2 = K_3 = 3$), where $C_1 =$ {square, circle, triangle}, $C_2 =$ {white, grey, black}, $C_3 =$ {big, small, medium}. The semantic information of each object is characterized from three dimensions, including shape, color and size. For example, the class vector of the object in top left corner corresponds to [square, white, small]$^{\textrm{T}}$.

The key challenge to learn from MDC data is the huge output space. Specifically, the number of class combinations in the output space will increase exponentially with the increase of dimensions (i.e., $\prod _{j=1}^{q} K_j$). Compared with the huge output space, the limited training samples often cannot cover all class combinations. For example, there are a total of 27 (i.e., $3^3$) possible class combinations in the above toy example while only 9 training examples are shown in Fig. 1. Moreover, even if one class combination appears in the training set, the number of training samples belonging to this class combination is usually very limited. From this perspective, the supervision information provided by the output space in MDC is very weak [50]. To effectively deal with the learning difficulty caused by the large output space, the commonly used learning strategy is to model the dependencies among class spaces to help the predictive model induction process. In this paper, we categorize existing specially designed MDC algorithms into two categories, namely explicit dependency-modeling algorithms and implicit dependency-modeling algorithms which will be discussed in Sections 3.2 and 3.3 respectively.

Table 2 Characteristics of publicly available benchmark MDC datasets

2.2 Evaluation metrics

To evaluate the generalization performance of MDC model, there are three metrics which have been widely used in recent MDC studies, i.e., Hamming Score (HS), Exact Match (EM) and Sub-Exact Match (SEM). Specifically, given the MDC test set $\mathcal {S}=\{(\varvec{x}_{i},\varvec{y}_{i}) \mid 1\le i\le p \}$ and the MDC model $f:\mathcal {X}\mapsto \mathcal {Y}$ to be evaluated, let ${\varvec{y}}_i = [y_{i1},y_{i2},\ldots ,y_{iq}]^{\textrm{T}} \in \mathcal {Y}$ and $\hat{\varvec{y}}_i=f({\varvec{x}}_i) = [\hat{y}_{i1},\hat{y}_{i2},\ldots ,\hat{y}_{iq}]^{\textrm{T}}$ be the ground-truth and predicted class vector for test example $\varvec{x}_i$, then the number of class labels for which f returns the correct predictions can be calculated via $r^{(i)}=\sum _{j=1}^{q} [\![ {y_{ij}=\hat{y}_{ij}} ]\!]$. Here, predicate $[\![ {\pi } ]\!]$ returns 1 if $\pi$ holds and 0 otherwise. The definitions of these three evaluation metrics can be formally formulated as follows:

• Hamming Score [21, 51,52,53,54]:

  $$\begin{aligned} {\textrm{HS}}_{\mathcal {S}}(f)=\frac{1}{p}\sum \limits _{i=1}^p \frac{1}{q}\cdot r^{(i)} \end{aligned}$$

  This metric measures the average fraction of dimensions which have been made correct classification by the MDC model f for one test example. HS is also equal to the average of dimension-wise accuracy if we regard MDC as a set of multi-class classification problems, one per dimension. In some literatures, HS is also termed as class accuracy [55], Hamming accuracy [56,57,58] or mean accuracy [16, 18, 38, 42, 59].

• Exact Match [21, 51,52,53, 60]:

  $$\begin{aligned} {\textrm{EM}}_{\mathcal {S}}(f)=\frac{1}{p}\sum \limits _{i=1}^p [\![ {r^{(i)}=q} ]\!] \end{aligned}$$

  This metric measures the proportion of test examples on which the MDC model f has classified all dimensions correctly. EM is also equal to the overall accuracy if we regard MDC as a single multi-class classification by treating each distinct class combination as a new class. Conceptually, this metric is very strict and its value might be very low when q is large. In some literatures, EM is also termed as example accuracy [55, 57, 58] or global accuracy [16, 18, 38, 42, 46, 56, 59].

• Sub-Exact Match:

  $$\begin{aligned} {\textrm{SEM}}_{\mathcal {S}}(f)=\frac{1}{p}\sum \limits _{i=1}^p [\![ {r^{(i)}\ge q-1} ]\!] \end{aligned}$$

  This metric measures the proportion of test examples on which the MDC model f has classified at least $q-1$ dimensions correctly. It is firstly introduced by Jia and Zhang [53] and corresponds to a relaxed version of EM.

According to the above definitions, it is easy to know that the larger the metric values, the better the generalization performance.

Fig. 2

Categorization of representative MDC algorithms being reviewed

2.3 Benchmark datasets

Publicly available datasets can greatly motivate the research in this area. Currently, there are a total of 24 MDC datasets that can be freely used for academic purpose². Table 2 briefly summarizes their key characteristics, including the number of examples (#Example, i.e., m), the number of dimensions (#Dim., i.e., q), the number of class labels in each dimension (#Label/Dim., i.e., $K_1, \ldots , K_q$), the number of features (#Feature, i.e., d). Note that, for the column “#Label/Dim.”, if $K_1 = \ldots = K_q = K$, then K is recorded. Otherwise, $K_1, \ldots , K_q$ will be recorded in turn. For the column “#Feature”, ‘n’ and ‘x’ denote numeric and nominal features, respectively. Here, three types of non-numeric features including discrete-valued features without/with ordinal relationship and binary-valued features are all referred to as nominal features. Besides, for each dataset, both the original reference (Orig. Refs.) and the reference where the dataset is firstly preprocessed as an MDC dataset (First in MDC) are also given in the last two columns, respectively.

3 Learning algorithms

In machine learning researches, the key issue for one learning setting is to develop new algorithms, which also holds for MDC. In this section, the technical details of several representative MDC algorithms are scrutinized. Specifically, Section 3.1 introduces two intuitive MDC algorithms that are the most commonly used baselines in MDC researches and should be beat by the newly proposed MDC algorithm. Sections 3.2-3.3 introduce six specially designed MDC algorithms, where the three algorithms introduced in Section 3.2 aim to explicitly consider the class dependencies and the three algorithms introduced in Section 3.3 aim to implicitly consider the class dependencies. Figure 2 summarizes the eight algorithms to be discussed in the rest of this section.

3.1 Intuitive algorithms

3.1.1 Binary relevance

The basic idea of binary relevance (BR) is to decompose the original MDC problem into q independent multi-class classification problems, one per dimension³.

Algorithm 1 Binary relevance for MDC

Fig. 3

An intuition for binary relevance based on the toy example in Fig. 1

Specifically, by focusing on the labeling information w.r.t. each dimension one by one, BR constructs q independent multi-class classification datasets as follows:

$$\begin{aligned} \mathcal {D}^{\textrm{BR}}_{{\textrm{m}}j}=\{({\varvec{x}}_i,y_{ij}) \mid 1 \le i \le m\},~(1 \le j \le q) \end{aligned}$$

(1)

Then, any off-the-shelf multi-class classification algorithm $\mathcal {M}$ can be utilized to induce a multi-class classifier $f_{{\textrm{m}}j}^{\textrm{BR}} \leftarrow \mathcal {M}\left( \mathcal {D}^{\textrm{BR}}_{{\textrm{m}}j}\right)$ over $\mathcal {D}^{\textrm{BR}}_{{\textrm{m}}j}$. Note that $y_{ij} \in C_j$, i.e., $f_{{\textrm{m}}j}^{\textrm{BR}}$ corresponds to the map** function from $\mathcal {X}$ to $C_j$.

With the learned q multi-class classifiers $f_{{\textrm{m}}1}^{\textrm{BR}}$, $f_{{\textrm{m}}2}^{\textrm{BR}}$, $\ldots$, $f_{{\textrm{m}}q}^{\textrm{BR}}$, given an unseen instance ${\varvec{x}}_*$, the j-th multi-class classifier $f_{{\textrm{m}}j}^{\textrm{BR}}$ can return a prediction for its j-th dimension, i.e., $f_{{\textrm{m}}q}^{\textrm{BR}}({\varvec{x}}_*)$. The final predicted class vector ${\varvec{y}}_*$ can be determined by simply concatenating the q predictions as follows:

$$\begin{aligned} {\varvec{y}}_* = \left[ f_{{\textrm{m}}1}^{\textrm{BR}}({\varvec{x}}_*), f_{{\textrm{m}}2}^{\textrm{BR}}({\varvec{x}}_*), \ldots , f_{{\textrm{m}}q}^{\textrm{BR}}({\varvec{x}}_*)\right] ^{\textrm{T}} \end{aligned}$$

(2)

Let $f^{\textrm{BR}}: \mathcal {X} \mapsto \mathcal {Y}$ be the MDC classifier induced by BR, it can be denoted as follows:

$$\begin{aligned} f^{\textrm{BR}} = \left[ f_{{\textrm{m}}1}^{\textrm{BR}}, f_{{\textrm{m}}2}^{\textrm{BR}}, \ldots , f_{{\textrm{m}}q}^{\textrm{BR}}\right] ^{\textrm{T}} \end{aligned}$$

(3)

Algorithm 1 presents the pseudocode of BR. Moreover, Fig. 3 shows an intuition for the learning procedure of BR to solve the toy example in Fig. 1. Specifically, BR independently trains three multi-class classifiers according to the labeling information w.r.t. shape, color, size. For unseen instance, its shape, color and size are determined by the three classifiers, respectively.

Algorithm 2 Class powerset for MDC

Fig. 4

An intuition for class powerset based on the toy example in Fig. 1

3.1.2 Class powerset

The basic idea of class powerset (CP) is to transform the original MDC problem into a single multi-class classification problem, where each distinct class combination in training set is regarded as a new class⁴.

Specifically, by regarding the labeling information in all dimensions as an entirety, CP constructs a multi-class classification dataset as follows:

$$\begin{aligned} \mathcal {D}_{\textrm{m}}^{\textrm{CP}}=\{({\varvec{x}}_i,\Lambda _{\mathcal {Y}}({\varvec{y}}_i)) \mid 1 \le i \le m\} \end{aligned}$$

(4)

Here, $\Lambda _{\mathcal {Y}}$ corresponds to an injective function from the q-dimensional output space $\mathcal {Y}$ to one single dimensional (categorical) output space $\mathcal {Y}^{\textrm{CP}}$. In other words, each distinct class combination in $\mathcal {Y}$ corresponds to a different item in $\mathcal {Y}^{\textrm{CP}}$, and vice versa. Then, any off-the-shelf multi-class classification algorithm $\mathcal {M}$ can be utilized to induce a multi-class classifier $f_{\textrm{m}}^{\textrm{CP}} \leftarrow \mathcal {M}\left( \mathcal {D}_{\textrm{m}}^{\textrm{CP}}\right)$ over $\mathcal {D}_{\textrm{m}}^{\textrm{CP}}$. It is easy to know that $f_{\textrm{m}}^{\textrm{CP}}$ corresponds to the map** function from $\mathcal {X}$ to $\mathcal {Y}^{\textrm{CP}}$.

With the learned multi-class classifier $f_{\textrm{m}}^{\textrm{CP}}$, given an unseen instance ${\varvec{x}}_*$, $f_{\textrm{m}}^{\textrm{CP}}$ can return a prediction, i.e., $f_{\textrm{m}}^{\textrm{CP}}({\varvec{x}}_*)$. Let $\Lambda ^{-1}_{\mathcal {Y}}$ be the corresponding inverse function of $\Lambda _{\mathcal {Y}}$, the final predicted class vector ${\varvec{y}}_*$ can be determined as follows:

$$\begin{aligned} {\varvec{y}}_* = \Lambda ^{-1}_{\mathcal {Y}}\left( f_{\textrm{m}}^{\textrm{CP}}({\varvec{x}}_*) \right) \end{aligned}$$

(5)

Let $f^{\textrm{CP}}: \mathcal {X} \mapsto \mathcal {Y}$ be the MDC classifier induced by CP, it can be denoted as follows:

$$\begin{aligned} f^{\textrm{CP}} = \Lambda ^{-1}_{\mathcal {Y}} \circ f_{\textrm{m}}^{\textrm{CP}} \end{aligned}$$

(6)

where $\circ$ denotes the composition of two functions.

Algorithm 2 presents the pseudocode of CP. Moreover, Fig. 4 shows an intuition for the learning procedure of CP to solve the toy example in Fig. 1. Specifically, CP regards the three-dimensional labeling information as an entirety (e.g., the big grey square and the big black square are two different classes) and trains a single multi-class classifier. For unseen instance, its shape, color and size can be interpreted from the single prediction returned by the learned multi-class classifier (e.g., the new class 4 corresponds to a big grey square).

3.1.3 Discussions

The principles of the two above algorithms are very intuitive and their implementations are very simple. In some cases, they can also achieve good classification performance. However, there are obvious disadvantages for each of them as well.

In MDC, all class spaces share the same input space, thus it is very likely that some dependencies exist among these class spaces. In fact, it is also the basic assumption of MDC, otherwise we just need to deal with each dimension one by one. However, due to the limited number of training samples, not all class combinations will appear in training set. BR deals with each dimension independently and then any potential dependencies among different dimensions are ignored (i.e., underfitting), which will impact its generalization ability. CP learns the classifier based on the class combinations in training set and cannot return class combinations which do not appear in training set (i.e., overfitting). Besides, the number of class combinations in training set is usually very large, especially for MDC tasks with large number of dimensions, which will lead to high computational complexity.

Therefore, it is not recommended to ignore or overfit class dependencies in training set like BR or CP. Existing works have shown that modeling class dependencies in proper way is the key for building effective MDC models. For existing MDC algorithms, according to their mechanisms of modeling class dependencies, we categorize them into two categories, namely explicit dependency-modeling algorithms and implicit dependency-modeling algorithms. In the following parts of this section, we will present six specially designed MDC algorithms from these two levels, three per each category.

3.2 Explicit dependency-modeling algorithms

The noteworthy characteristics of such algorithms are to explicitly modeling the class dependencies through some kind of structure.

Algorithm 3 Decomposition-based classifier chains for MDC

3.2.1 Decomposition-based classifier chains

The basic idea of decomposition-based classifier chains (DCC) is to build a chain of binary classifiers to solve the MDC problem [79].

Specifically, by decomposing the original MDC problem via one-vs-one strategy w.r.t. each dimension, DCC transforms the MDC problem into a set of binary classification problems. It is easy to know that there are a total of $T = \sum _{j=1}^{q} \left( {\begin{array}{c}K_j\\ 2\end{array}}\right)$ decomposed binary classification problems. Formally, for the t-th decomposed problem ($1 \le t \le T$), let $p_t$ (or $n_t$) be the corresponding positive (or negative) class, and $\mathcal {I}_{+}^{t}$ (or $\mathcal {I}_{-}^{t}$) be the index set of samples which belong to $p_t$ (or $n_t$), the t-th decomposed problem corresponds to the following binary classification dataset:

$$\begin{aligned} \mathcal {D}_{\textrm{b}}^{t} = \{ (\varvec{x}_i, l_{i}^{t}) \mid i \in \mathcal {I}_{+}^{t} \cup \mathcal {I}_{-}^{t} \}, \nonumber \\ \text {where}~l_{i}^{t} = \left\{ \begin{array}{ll} 1,&{} i \in \mathcal {I}_{+}^{t}\\ 0,&{} i \in \mathcal {I}_{-}^{t} \end{array}\right. \end{aligned}$$

(7)

To solve the above T binary classification problems, DCC chooses to build a chain of binary classifiers to consider their correlations. Let $\Psi (T) = \{ \psi (1), \psi (2), \ldots , \psi (T) \}$ be one order over 1 to T (e.g., {1, 3, 2, 4} is one order over 1 to 4), the $\psi (t)$-th binary classifier $f_{{\textrm{b}}}^{\psi (t)}$ is trained over the following dataset:

$$\begin{aligned} \mathcal {D}_{\textrm{bo}}^{\psi (t)} = \left\{ \left(\varvec{x}_i^{\psi (t)}, l_{i}^{\psi (t)}\right) \mid i \in \mathcal {I}_{+}^{\psi (t)} \cup \mathcal {I}_{-}^{\psi (t)} \right\}, \nonumber \\ \text {where}~\varvec{x}_{i}^{\psi (t)} = \left[ \varvec{x}_i; \hat{l}_{i}^{\psi (1)}; \ldots ; \hat{l}_{i}^{\psi (t-1)}\right] \end{aligned}$$

(8)

i.e., $f_{{\textrm{b}}}^{\psi (t)} \leftarrow \mathcal {B}\left(\mathcal {D}_{\textrm{bo}}^{\psi (t)}\right)$. Here, $\hat{l}_{i}^{\psi (t)} = f_{{\textrm{b}}}^{\psi (t)}\left(\varvec{x}_{i}^{\psi (t)}\right)$ and $\mathcal {B}$ denotes the employed binary classification algorithm. Note that $\mathcal {D}_{\textrm{bo}}^{\psi (t)}$ is constructed based on $\mathcal {D}_{\textrm{b}}^{\psi (t)}$, where DCC utilizes the predictions of preceding binary classifiers on the chain to augment the feature space for training the subsequent binary classifiers. For the first binary classification problem on the chain, it is easy to know that $\mathcal {D}_{\textrm{bo}}^{\psi (1)}$ is exactly $\mathcal {D}_{\textrm{b}}^{\psi (1)}$.

With the learned T binary classifiers, given an unseen instance ${\varvec{x}}_*$, each binary classifier $f_{{\textrm{b}}}^{\psi (t)}$ will return a binary prediction ($1 \le t \le T$):

$$\begin{aligned} \hat{l}_{*}^{\psi (t)}{} & {} = f_{{\textrm{b}}}^{\psi (t)}\left(\varvec{x}_{*}^{\psi (t)}\right), \nonumber \\{} & {} \text {where}~\varvec{x}_{*}^{\psi (t)} = \left[ \varvec{x}_*; \hat{l}_{*}^{\psi (1)}; \ldots ; \hat{l}_{*}^{\psi (t-1)}\right] . \end{aligned}$$

(9)

Finally, based on the T binary predictions, its class vector $\varvec{y}_* = [y_{*1}, \ldots , y_{*q}]^{\textrm{T}}$ can be determined via one-vs-one decoding rule w.r.t. each dimension. Algorithm 3 presents the pseudocode of DCC⁵.

In practice, the chaining order $\Psi (T)$ determines the causal relationships among the T binary classification problems and will affect the performance of DCC. Moreover, it is also very hard to obtain the optimal chaining order. Then, Jia and Zhang [79] further propose to make an ensemble of some candidate DCC classifiers with random chaining orders, leading to the ensembles of decomposition-based classifier chains (EDCC).

DCC can be regarded as an improved version of BR via modeling class dependencies with a chaining structure. This algorithm originates from the classifier chains for multi-label classification [80] which has inspired large number of works in different fields⁶ and can be naturally generalized into MDC. Earlier classifier chains-based works on MDC [51, 52, 59] mainly focus on finding better chaining orders, just like many multi-label works have done [81]. Different from these works, DCC considers the multi-class nature of each dimension in MDC and builds a chain of binary classifiers like the initial multi-label classifier chains, which suggests a new perspective for develo** classifier chains-based MDC algorithms. Similar to DCC, M3MDC also decomposes the original MDC problem via one-vs-one strategy w.r.t. each dimension while considers the class dependencies by introducing covariance regularization [69]. On the other hand, the recently proposed IMAM [82] improves BR by learning a shared feature embedding as well as distilling the knowledge from a pretrained BR model.

3.2.2 Super-class classifier

The basic idea of super-class classifier (SC) is to partition the class spaces into several groups (i.e., super-classes) by measuring conditional class dependencies [55].

Specifically, by firstly learning a BR classifier (cf. Section 3.1.1) over training set, SC measures the conditional class dependencies via calculating three types of dimension-wise prediction errors. Let $\hat{y}_{ij}$ be the corresponding prediction of class label $y_{ij}$ by the learned BR classifier, for each pair of dimensions (e.g., the j-th and k-th dimension where $1 \le j, k \le q$), SC defines three types of measured frequencies $M_e(j,k)$ and expected frequencies $E_e(j,k)$ as follows ($1 \le e \le 3$):

$$\begin{aligned} M_1(j,k) ={} & {} \frac{1}{N}\sum \limits _{i=1}^{N} \left( [\![ {y_{ij}=\hat{y}_{ij}} ]\!] \wedge [\![ {y_{ik}=\hat{y}_{ik}} ]\!]\right) \\ E_1(j,k) ={} & {} \frac{1}{N}\sum \limits _{i=1}^{N} [\![ {y_{ij}=\hat{y}_{ij}} ]\!] \cdot \frac{1}{N}\sum \limits _{i=1}^{N} [\![ {y_{ik}=\hat{y}_{ik}} ]\!]\\ M_2(j,k) ={} & {} \frac{1}{N}\sum \limits _{i=1}^{N} \left( [\![ {y_{ij} \ne \hat{y}_{ij}} ]\!] \wedge [\![ {y_{ik} \ne \hat{y}_{ik}} ]\!]\right) \\ E_2(j,k) ={} & {} \frac{1}{N}\sum \limits _{i=1}^{N} [\![ {y_{ij} \ne \hat{y}_{ij}} ]\!] \cdot \frac{1}{N}\sum \limits _{i=1}^{N} [\![ {y_{ik} \ne \hat{y}_{ik}} ]\!]\\ M_3(j,k) ={} & {} \frac{1}{N}\sum \limits _{i=1}^{N} \left( [\![ {y_{ij} = \hat{y}_{ij}} ]\!] \oplus [\![ {y_{ik} = \hat{y}_{ik}} ]\!]\right) \\ E_3(j,k) ={} & {} 1-E_1(j,k)-E_2(j,k) \end{aligned}$$

where $\wedge$ and $\oplus$ denote the “logical and” and “logical exclusive OR” operations. $N$  denotes the number of samples in training set $\mathcal{D}$ used for testing (i.e., $\mathcal{D}_{\rm te}$ in Algorithm~4). The predicate $[\![ {\pi } ]\!]$ returns 1 if $\pi$ holds and 0 otherwise as previously stated.

Then, based on the above six frequencies, SC calculates the conditional-dependence chi-squared statistic $\bar{\chi }_{jk}^2$ between the j-th and k-th dimension as follows:

$$\begin{aligned} \bar{\chi }_{jk}^2 = \sum \limits _{e=1}^{3} \frac{(M_e(j,k) - E_e(j,k))^2}{E_e(j,k)} - \bar{\chi }_{\textrm{C}}^2 \end{aligned}$$

(10)

where $\bar{\chi }_{\textrm{C}}^2$ denotes the critical value for two degrees of freedom. The larger the value of $\bar{\chi }_{jk}^2$ is, the more dependencies between the pair of dimensions exist.

For one valid class partition $\theta = \{ S_1, \ldots , S_{|\theta |} \}$, the two conditions $S_1 \cup \ldots \cup S_{|\theta |} = \{1, \ldots , q\}$ and $S_u \cap S_v = \varnothing$ always hold, where $|\cdot |$ returns the cardinality of one set and $1 \le u < v \le |\theta |$. To evaluate whether $\theta$ is a good partition, SC calculates a score $\pi (\theta )$ based on the above chi-squared statistic as follows:

$$\begin{aligned} \pi (\theta ) = \sum \limits _{j,k \mid \exists S: \{j,k\} \subseteq S } \bar{\chi }_{jk}^2 - \sum \limits _{j,k \mid \not \exists S: \{j,k\} \subseteq S } \bar{\chi }_{jk}^2 \end{aligned}$$

(11)

Therefore, $\pi (\theta )$ corresponds to the difference between the sum of $\bar{\chi }_{jk}^2$s for all pairs of dimensions in the same set (i.e., $\sum _{j,k \mid \exists S: \{j,k\} \subseteq S } \bar{\chi }_{jk}^2$) and the sum of $\bar{\chi }_{jk}^2$s for all pairs of dimensions in different sets (i.e., $\sum _{j,k \mid \not \exists S: \{j,k\} \subseteq S } \bar{\chi }_{jk}^2$). Generally speaking, dimensions with strong dependencies should be partitioned into the same set, while dimensions with weak dependencies should be partitioned into different sets. In other words, the larger the value of $\pi (\theta )$, the better the class partition $\theta$.

After all statistics $\bar{\chi }_{jk}^2$s are obtained, for one specific class partition $\theta$, it is very efficient to calculate its $\pi (\theta )$. Thus, we just need to find the partition $\theta$ with largest $\pi (\theta )$. However, for one MDC task with q dimensions, the number of possible partitions corresponds to the q-th Bell number $B_q = \sum _{k=0}^{q-1} \left( {\begin{array}{c}q-1\\ k\end{array}}\right) B_k$ where $B_0=1$. Thus, it is intractable to traverse all possible partitions. For this issue, SC attempts to find a good and acceptable partition via simulated annealing [83] instead of exhaustively searching the best one. Specifically, given one valid class partition $\theta = \{ S_1, \ldots , S_{|\theta |} \}$, SC randomly mutates it into a new one $\theta '$ via the following procedure:

$\theta '=$ Mutate($\theta$)
Randomly select j from $\{1,2,\ldots ,q\}$
and l from $\{1,2,\ldots ,{|\theta |}\}$;
if $j \in S_{l}$ then
Move j from $S_{l}$ into a new set $\{j\}$;
else
Move j from its original set into $S_{l}$;
end if

To decide whether the new $\theta '$ should be accepted to update $\theta$, there are two different cases. (1) If $\pi (\theta ') > \pi (\theta )$, then $\theta$ is updated with the better $\theta '$. (2) If $\pi (\theta ') < \pi (\theta )$, $\theta '$ will also be accepted with a certain probability. Specifically, a random number u is drawn uniformly in the range of [0, 1]. If $e^{(\pi (\theta ')-\pi (\theta ))/T}>u$, then $\theta$ is updated with $\theta '$. Otherwise, $\theta$ will be kept unchanged. Here, T denotes the temperature and is initialized with some value. The value of T will be decreased in each iteration until it is below a certain threshold, i.e., annealing process. Because $e^{(\pi (\theta ')-\pi (\theta ))/T}>1$ always holds when $\pi (\theta ') > \pi (\theta )$ and the random number u is always not greater than 1, then the above two update conditions can be uniformly expressed as $e^{(\pi (\theta ')-\pi (\theta ))/T}>u$.

Algorithm 4 Super-class classifier for MDC

When the partition $\theta = \{ S_1, \ldots , S_{|\theta |} \}$ is determined, for each MDC training example $({\varvec{x}}_i, {\varvec{y}}_i) \in \mathcal {D}$, let ${\varvec{y}}_{iS_l}$ ($1 \le l \le |\theta |$) be the corresponding length-$|S_l|$ class vector that only contains class labels of dimensions in $S_l$ (e.g., if $S_l = \{1, 3\}$, then ${\varvec{y}}_{iS_l} = [y_{i1}, y_{i3}]^{\textrm{T}}$), SC transforms ${\varvec{y}}_{iS_l}$ into a new class $\Lambda _{\mathcal {Y}_{S_l}}({\varvec{y}}_{iS_l})$ where $\mathcal {Y}_{S_l}$ denotes the Cartesian product of the class spaces in $S_l$ (e.g., if $S_l = \{1, 3\}$, then $\mathcal {Y}_{S_l} = C_1 \times C_3$). Here, similar to $\Lambda _{\mathcal {Y}}$ in CP (cf. Fig. 4 for an intuition), $\Lambda _{\mathcal {Y}_{S_l}}$ also corresponds to an injective function from the $|S_l|$-dimensional output space $\mathcal {Y}_{S_l}$ to one single dimensional (categorical) output space $\mathcal {Y}_{S_l}^{\textrm{CP}}$. Then, the original length-q class vector ${\varvec{y}}_i$ can be converted into a length-$|\theta |$ vector ${\varvec{y}}_i^{\theta } = [\Lambda _{\mathcal {Y}_{S_1}}({\varvec{y}}_{iS_1}), \ldots , \Lambda _{\mathcal {Y}_{S_{|\theta |}}}({\varvec{y}}_{iS_{|\theta |}})]^{\textrm{T}}$. For convenience, the whole class space transformation is denoted as $\Lambda _{({\mathcal {Y}},{\theta })}$, i.e., ${\varvec{y}}_i^{\theta } = \Lambda _{({\mathcal {Y}},{\theta })}({\varvec{y}}_i)$ and ${\varvec{y}}_i = \Lambda _{({\mathcal {Y}},{\theta })}^{-1}({\varvec{y}}_i^{\theta })$ where $\Lambda _{({\mathcal {Y}},{\theta })}^{-1}$ denotes the corresponding inverse function of $\Lambda _{({\mathcal {Y}},{\theta })}$. Thus, the original MDC dataset is transformed into the following new dataset:

$$\begin{aligned} \mathcal {D}^{\theta } = \left\{\left({\varvec{x}}_i, {\varvec{y}}_i^{\theta }\right) \mid 1 \le i \le m \right\} \end{aligned}$$

(12)

Obviously, $\mathcal {D}^{\theta }$ corresponds to an MDC problem with $|\theta |$ dimensions. In other words, SC considers all dimensions in each super-class $S_j$ as a new dimension, where each distinct class combination in the same super-class is regarded as a new class. Compared with the original MDC problem, the newly obtained one has less dimensions as some dimensions are combined as a single one. Because the dimensions with strong dependencies have been grouped as super-classes, the newly obtained MDC problem is considered to be easier to solve. Generally, any off-the-shelf MDC algorithm can be used to solve the newly obtained MDC problem. In the MEKA software [84], Read et al. use classifier chains by default to solve the resulted MDC problem when implementing the super-class classifier. Note that the CP algorithm introduced in Section 3.1.2 cannot be used here because it will result in the same prediction with the standard CP algorithm. Algorithm 4 presents the pseudocode of SC⁷.

It is easy to know that the superclass partition process works in filter manner. Read et al. [55] also propose to finetune the resulted partition in wrapper manner which is denoted as SC’. But according to the reported experimental results, SC’ achieves no significant performance improvement against SC but takes a much longer time. Therefore, we just focus on the standard version in this paper. In practice, it cannot be expected that one specific super-class partition can model all dependencies among dimensions for an MDC task. Then, Read et al. [55] further propose to make an ensemble of some candidate SC classifiers with different class partitions, leading to the ensembles of super-classes classifiers (ESC).

SC can be regarded as an improved version of CP. The idea of super-class partition can mitigate the huge class combinations problem in CP and then class combinations not appearing in training set might also be returned by SC. It inspires the pairwise grou** operation in following works to consider the dependencies between two dimensions [56, 67, 71, 74]. SC has been usually used as a compared algorithm in MDC researches and the corresponding paper has received 65 citations according to Google Scholar statistics (by February 2024).

Algorithm 5 Stacked dependency exploitation for MDC

3.2.3 Stacked dependency exploitation for MDC

The basic idea of stacked dependency exploitation for MDC (SEEM) is to consider the class dependencies in a two-level manner, where the dependencies between each pair of dimensions and the dependencies between each dimension and the remaining dimensions are considered in the first level and second level, respectively [71].

Specifically, in the first level, by learning a CP classifier (cf. Section 3.1.2) for each pair of dimension, SEEM considers second-order dependencies residing in training set. Let $f_{rs}^{\textrm{CP}}$ be the corresponding CP classifier for r-th and s-th dimensions ($1 \le r < s \le q$), $f_{rs}^{\textrm{CP}}$ is induced based on the following two-dimensional classification dataset:

$$\begin{aligned} \mathcal {D}^{rs} = \left\{ \left({\varvec{x}}_i, {\varvec{y}}_i^{rs}\right) \mid 1 \le i \le m \right\} \end{aligned}$$

(13)

where ${\varvec{y}}_i^{rs} = [y_{ir}, y_{is}]^{\textrm{T}}$. Then, for any input ${\varvec{x}}_i$, its class labels w.r.t. r-th and s-th class spaces can be recovered by $\hat{\varvec{y}}_i^{rs} = [\hat{y}_{ir}^{rs}, \hat{y}_{is}^{rs}]^{\textrm{T}} = f_{rs}^{\textrm{CP}}({\varvec{x}}_i)$. Here, the basic assumption of SEEM is that the dependencies between two dimensions are easier to consider than the dependencies among many dimensions with limited training samples.

It is easy to know there are a total of $\left( {\begin{array}{c}q\\ 2\end{array}}\right)$ pairwise CP classifiers $f_{rs}^{\textrm{CP}}$s and $q-1$ predictions will be returned w.r.t. each dimension for any input ${\varvec{x}}_i$. Let $\hat{\varvec{y}}_{ij}$ be the $q-1$ predictive outputs w.r.t. the j-th dimension ($1 \le j \le q$):

$$\begin{aligned} \hat{\varvec{y}}_{ij} = \left[ \hat{y}_{ij}^{1j}, \ldots , \hat{y}_{ij}^{(j-1)j},\hat{y}_{ij}^{j(j+1)}, \ldots ,\hat{y}_{ij}^{jq} \right] ^{\textrm{T}} \end{aligned}$$

(14)

Here, each item in $\hat{\varvec{y}}_{ij}$ comes from one pairwise CP classifier which considers the dependency between the j-th dimension and another one dimension. Then, $\hat{\varvec{y}}_{ij}$ contains the dependencies between the j-th dimension and all the remaining dimensions. To determine the final prediction w.r.t the j-th dimension for input $\varvec{x}_i$, one can surely make majority voting based on the $q-1$ items in $\hat{\varvec{y}}_{ij}$, but SEEM utilizes a subtler way in the second level.

Generally speaking, the generalization ability of one classifier varies for different samples. To consider this difference, SEEM chooses to estimate the local generalization ability of one classifier for any input $\varvec{x}_i$ by calculating the accuracy in its k nearest neighbors. Let $n_{ir}^{rs}$ and $n_{is}^{rs}$ be the number of samples in any input ${\varvec{x}_i}$’s k nearest neighbors on which $f_{rs}^{\textrm{CP}}$ makes correct classification over the r-th and s-th dimension respectively, the estimated local generalization abilities of $f_{rs}^{\textrm{CP}}$ for ${\varvec{x}}_i$ correspond to:

$$\begin{aligned} \eta _{ir}^{rs} = \frac{n_{ir}^{rs}}{k},~~\eta _{is}^{rs} = \frac{n_{is}^{rs}}{k} \end{aligned}$$

(15)

To merge these estimated abilities into the $q-1$ predictions in $\hat{\varvec{y}}_{ij}$, for each prediction (denote by $\hat{y}_{ij}^{rj}$ if $r<j$ or $\hat{y}_{ij}^{jr}$ if $r>j$, $1\le r \ne j \le q$, we take $\hat{y}_{ij}^{rj}$ as an example in the following Eqs. (16) and (17)), SEEM transforms it into a length-$K_j$ row vector:

$$\begin{aligned} \varvec{\delta }_{ij}^{rj} = \left[ \delta _{ij}^{rj}(1), \delta _{ij}^{rj}(2), \ldots , \delta _{ij}^{rj}(K_j)\right] \end{aligned}$$

(16)

where $\delta _{ij}^{rj}(a)$ is equal to $+1$ if $\hat{y}_{ij}^{rj} = c_a^j$ and $-1$ otherwise. Then, we can re-scale $\varvec{\delta }_{ij}^{rj}$ with its corresponding estimated generalization ability $\eta _{ij}^{rj}$ to yield the following vector:

$$\begin{aligned} \varvec{\zeta }_{ij}^{rj} = \eta _{ij}^{rj} \cdot \varvec{\delta }_{ij}^{rj} \end{aligned}$$

(17)

By concatenating the $q-1$ different above re-scaled vectors, SEEM transforms $\hat{\varvec{y}}_{ij}$ into a new vector ${\varvec{z}}_{ij}$ with length $(q-1) \cdot K_j$ as follows:

$$\begin{aligned} {\varvec{z}}_{ij} = \left[ \varvec{\zeta }_{ij}^{1j}, \ldots , \varvec{\zeta }_{ij}^{(j-1)j},\varvec{\zeta }_{ij}^{j(j+1)}, \ldots ,\varvec{\zeta }_{ij}^{jq} \right] ^{\textrm{T}} \end{aligned}$$

(18)

After traversing the training set, SEEM can construct the following multi-class classification dataset for each dimension:

$$\begin{aligned} \mathcal {D}_{\textrm{m}}^{j}=\{({\varvec{z}}_{ij},y_{ij})\mid 1\le i\le m\},~~(1\le j \le q) \end{aligned}$$

(19)

Based on $\mathcal {D}_{\textrm{m}}^{j}$, SEEM can learn a multi-class classifier $f_{\textrm{m}}^{j}$ by any off-the-shelf multi-class classification algorithm $\mathcal {M}$, i.e., $f_{\textrm{m}}^{j} \leftarrow \mathcal {M}(\mathcal {D}_{\textrm{m}}^{j})$. For any input $\varvec{x}_i$, the learned classifier $f_{\textrm{m}}^{j}$ can be used to combine the $q-1$ predictions w.r.t. the j-th dimension returned by pairwise CP classifiers in the first level. Note that $\mathcal {D}_{\textrm{m}}^{j}$ in Eq. (19) is similar to $\mathcal {D}^{\textrm{BR}}_{{\textrm{m}}j}$ in Eq. (1), the only difference is the input feature in $\mathcal {D}_{\textrm{m}}^{j}$ is constructed based on the predictions in the first level. Therefore, the learning strategy in the second level can be regarded as an improve version of BR.

With the pairwise CP classifiers in the first level and improved BR classifier in the second level, given an unseen instance ${\varvec{x}}_*$, SEEM first constructs a vector ${\varvec{z}}_{*j}$ for each dimension based on the predictions of corresponding pairwise CP classifiers ($1\le j \le q$). Then, its class label w.r.t. the j-th dimension can be obtained by $y_{*j} = f_{\textrm{m}}^{j}({\varvec{z}}_{*j})$. Finally, the predicted class vector ${\varvec{y}}_* = \left[ y_{*1},y_{*2},\ldots ,y_{*q}\right] ^{\textrm{T}}$ can be obtained by concatenating all predictions after traversing all dimensions. Algorithm 5 presents the pseudocode of SEEM⁸.

SEEM can be regarded as a complex of CP (in the first level) and BR (in the second level), but overcomes their respective shortcomings. Moreover, the two-level dependency modeling strategy makes it have good generalization performance. Similar works include FMC [56] and MDKNN [74], which also consider pairwise class dependencies in the first level and then synergize preliminary predictions to predict the final class vector in the second level. Its two-level working mechanism inspires the following MDC works on label coding [65, 67].

3.3 Implicit dependency-modeling algorithms

The noteworthy characteristics of such algorithms are to transform the original MDC problem into a new problem but without explicit dependency modeling mechanism in the transformation procedure.

Algorithm 6 One-hot multi-label transformation for MDC

3.3.1 One-hot multi-label transformation

The basic idea of one-hot multi-label transformation (OMLT)⁹ is to convert the multi-dimensional categorical output space in MDC into a binary-valued one similar to multi-label classification via one-hot conversion dimension-wisely, and then many off-the-shelf multi-label algorithms can be adapted to solve the newly obtained problem [57].

Specifically, by conducting one-hot conversion for the class label in each dimension, OMLT transforms one q-dimensional categorical class vector into L-dimensional binary-valued label vector where $L=\sum _{j=1}^{q} K_j$. For any training sample $\varvec{x}_i$, its class label $y_{ij} \in C_j= \left\{c^j_1,c^j_2,\ldots ,c^j_{K_j}\right\}$ can be converted into a length-$K_j$ binary vector ${\varvec{z}}_{ij} = \left[l_1^j, l_2^j, \ldots , l_{K_j}^j\right] \in \{0,1\}^{K_j}$, where $l_a^j = 1$ if $y_{ij} = c_a^j$ and $l_a^j = 0$ otherwise ($1 \le a \le K_j$)¹⁰. OMLT concatenates the q binary-valued vectors ${\varvec{z}}_{ij}$s together as ${\varvec{z}}_i = [{\varvec{z}}_{i1}, {\varvec{z}}_{i2}, \ldots , {\varvec{z}}_{iq}]^{\textrm{T}} \in \{0,1\}^L$. Then, the original MDC dataset can be transformed into a new dataset similar to multi-label classification as follows:

$$\begin{aligned} \mathcal {D}' = \{ ({\varvec{x}}_i, {\varvec{z}}_i) \mid 1 \le i \le m \} \end{aligned}$$

(20)

The above resulted problem can be solved by adapting many off-the-shelf multi-label algorithms. Nevertheless, Ma and Chen [57] further proposed a novel distance metric learning based formulation for the newly obtained problem as follows:

$$\begin{aligned} \min _{\textbf{W}} \left\| \textbf{Z} - \textbf{XW} \right\| _{\textbf{M}}^2 + \gamma \left\| \textbf{W} \right\| _{\textrm{F}}^2 \end{aligned}$$

(21)

Here, $\gamma \ge 0$ is one trade-off parameter, $\textbf{X}$ denotes the $m \times d$ instance matrix where the i-th row of $\textbf{X}$ corresponds to the transpose of $\varvec{x}_i$, $\textbf{Z}$ denotes the $m \times L$ label matrix after transformation where the i-th row of $\textbf{Z}$ corresponds to the transpose of $\varvec{z}_i$, $\textbf{W}$ denotes the $d \times L$ model parameter matrix to be determined, and $\textbf{M}$ denotes the distance matrix which is a L-th order square matrix. For any input $\varvec{x}_i$, the distance matrix $\textbf{M}$ aims at making its prediction $\textbf{W}^{\textrm{T}} {\varvec{x}}_i$ and label vector $\varvec{z}_i$ closer, while making its prediction $\textbf{W}^{\textrm{T}} {\varvec{x}}_i$ and other label vectors farther. Therefore, the distance matrix $\textbf{M}$ is determined as follows:

$$\begin{aligned} \min _{\textbf{M}}{} & {} \sum \limits _{i=1}^{m} \Bigl ( \left\| \textbf{W}^{\textrm{T}} {\varvec{x}}_i - {\varvec{z}}_i \right\| _{\textbf{M}}^2 \nonumber \\{} & {} + \frac{1}{k} \sum \limits _{j \in \mathcal {N}_k(\varvec{z}_i)} \left\| \textbf{W}^{\textrm{T}} {\varvec{x}}_i - {\varvec{z}}_j \right\| _{\textbf{M}^{-1}}^2 \Bigr ) + \lambda D_{\textrm{sld}}(\textbf{M},\textbf{I}) \end{aligned}$$

(22)

where $\lambda \ge 0$ is another trade-off parameter, $\mathcal {N}_k(\varvec{z}_i)$ is the index set of $\varvec{z}_i$’s k nearest neighbors identified in the transformed label space, $\textbf{I}$ is the identity matrix and $D_{\textrm{sld}}(\textbf{M},\textbf{I})$ is the symmetrized LogDet divergence defined as follows:

$$\begin{aligned} D_{\textrm{sld}}(\textbf{M},\textbf{I}) \triangleq {\textrm{tr}}(\textbf{M}) + {\textrm{tr}}\left( \textbf{M}^{-1}\right) - 2L \end{aligned}$$

Formulations (21) and (22) interact with each other, which leads to that $\textbf{W}$ and $\textbf{M}$ should be solved alternately. When $\textbf{M}$ is fixed, to determine $\textbf{W}$ via optimizing Eq. (21), we can calculate the gradient of its objective function w.r.t. $\textbf{W}$ and set the gradient to zero. Then $\textbf{W}$ can be obtained by solving the following Sylvester equation¹¹:

$$\begin{aligned} \textbf{X}^{\textrm{T}}\textbf{X}\textbf{W} + \gamma \textbf{W}\textbf{M}^{-1} = \textbf{X}^{\textrm{T}}\textbf{Z} \end{aligned}$$

(23)

When $\textbf{W}$ is fixed, to determine $\textbf{M}$ via optimizing Eq. (22), we can also calculate the gradient of its objective function w.r.t. $\textbf{M}$ and set the gradient to zero [85], leading to the following equation:

$$\begin{aligned} (\textbf{S} + \lambda \textbf{I}) - \textbf{M}^{-1} (\textbf{D} + \lambda \textbf{I}) \textbf{M}^{-1} = 0 \end{aligned}$$

(24)

Here, $\textbf{S}$ and $\textbf{D}$ are defined as follows:

$$\begin{aligned} \textbf{S}{} & {} \triangleq \sum \limits _{i=1}^{m} \left( \textbf{W}^{\textrm{T}} {\varvec{x}}_i - {\varvec{z}}_i\right) \left( \textbf{W}^{\textrm{T}} {\varvec{x}}_i - {\varvec{z}}_i\right) ^{\textrm{T}} \end{aligned}$$

(25)

$$\begin{aligned} \textbf{D}{} & {} \triangleq \sum \limits _{i=1}^{m} \frac{1}{k} \sum \limits _{j \in \mathcal {N}_k(\varvec{z}_i)} \left( \textbf{W}^{\textrm{T}} {\varvec{x}}_i - {\varvec{z}}_j\right) \left( \textbf{W}^{\textrm{T}} {\varvec{x}}_i - {\varvec{z}}_j\right) ^{\textrm{T}} \end{aligned}$$

(26)

By left and right multiplication of matrix $\textbf{M}$, Eq. (24) can be further reformulated as the following equivalent equation:

$$\begin{aligned} \textbf{M}(\textbf{S} + \lambda \textbf{I})\textbf{M} = (\textbf{D} + \lambda \textbf{I}) \end{aligned}$$

(27)

Here, Eq. (27) is a Riccati equation and has unique closed-form solution [86]:

$$\begin{aligned} \textbf{M} = (\textbf{S} + \lambda \textbf{I})^{-1} \#_{1/2}(\textbf{D} + \lambda \textbf{I}) \end{aligned}$$

(28)

where $\textbf{A}\#_{1/2}\textbf{B}$ corresponds to the midpoint of the geodesic joining $\textbf{A}$ to $\textbf{B}$:

$$\begin{aligned} \textbf{A}\#_{1/2}\textbf{B} \triangleq \textbf{A}^{1/2}(\textbf{A}^{-1/2}\textbf{B}\textbf{A}^{-1/2})^{1/2}\textbf{A}^{1/2} \end{aligned}$$

(29)

Following [85], Ma and Chen [57] further generalize Eq. (28) as follows:

$$\begin{aligned} \textbf{M} = (\textbf{S} + \lambda \textbf{I})^{-1} \#_{t}(\textbf{D} + \lambda \textbf{I}),~~t\in [0,1] \end{aligned}$$

(30)

where $\textbf{A}\#_{t}\textbf{B}$ corresponds to some inter-point of the geodesic joining $\textbf{A}$ to $\textbf{B}$:

$$\begin{aligned} \textbf{A}\#_{t}\textbf{B} \triangleq \textbf{A}^{1/2}\left( \textbf{A}^{-1/2}\textbf{B}\textbf{A}^{-1/2}\right) ^{t}\textbf{A}^{1/2} \end{aligned}$$

(31)

This generalization makes the solution of $\textbf{M}$ no longer restricted to midpoint of the geodesic joining $(\textbf{S} + \lambda \textbf{I})^{-1}$ to $(\textbf{D} + \lambda \textbf{I})$.

The solution of $\textbf{W}$ and $\textbf{M}$ can be obtained by initializing $\textbf{M} = \textbf{I}$ and then repeatedly determining $\textbf{W}$ and $\textbf{M}$ until convergence. This algorithm is named as gMML-I which is short for geometric metric mean learning (iteration).

With the learned $\textbf{W}$ and $\textbf{M}$, given an unseen instance ${\varvec{x}}_*$, a corresponding vector can be obtained by optimizing the following problem:

$$\begin{aligned} \min _{{\varvec{v}}_*} \frac{1}{2} \left\| {\varvec{v}}_* - \textbf{W}^{\textrm{T}}{\varvec{x}}_* \right\| _\textbf{M}^2 \end{aligned}$$

(32)

where ${\varvec{v}}_* = [{\varvec{v}}_{*1}, {\varvec{v}}_{*2}, \ldots , {\varvec{v}}_{*q}]^{\textrm{T}} \in \mathbb {R}^L$, the length of ${\varvec{v}}_{*j}$ is equal to $K_j$ and the sum of items in ${\varvec{v}}_{*j}$ must be equal to 1. Based on the obtained ${\varvec{v}}_*$, the final prediction w.r.t. each dimension can be respectively determined as follows ($1 \le j \le q$):

$$\begin{aligned} y_{*j} = c_{\hat{a}},~{\textrm{where}}~\hat{a} = \underset{1 \le a \le K_j}{\arg \max }~v_{*j}(a) \end{aligned}$$

(33)

Here, $v_{*j}(a)$ denotes the a-th item in ${\varvec{v}}_{*j}$. The final predicted class vector corresponds to the concatenation of dimension-wise predictions, i.e., ${\varvec{y}}_* = \left[ y_{*1},y_{*2},\ldots ,y_{*q}\right] ^{\textrm{T}}$. Algorithm 6 presents the pseudocode of OMLT¹².

OMLT initiates the dimension-wise label space transformation via one-vs-rest decomposition for MDC. The following works DLEM [65] and PLEM [87] conduct the label space transformation via one-vs-one decomposition. Moreover, OMLT aims at directly inducing predictive model in binary-valued label space, while DLEM and PLEM further enrich the decomposed space via label enhancement techniques [88].

Algorithm 7 Sparse label encoding for MDC

3.3.2 Sparse label encoding for MDC

The basic idea of sparse label encoding for MDC (SLEM) is to convert the multi-dimensional categorical output space in MDC into a real-valued one by using one binary-valued space as the intermediate bridge whose sparsity will be further utilized in the prediction phase [67].

Specifically, SLEM transforms the output space into a new one via three cascaded steps, including pairwise grou**, one-hot conversion and sparse label encoding, where the first two steps transform any class vector to a sufficiently sparse binary-valued vector which will be further transformed into a real-valued label vector by the last step. Firstly, pairwise grou** transforms the q-dimensional output space $\mathcal {Y}=C_1 \times C_2 \times \cdots \times C_q$ into $\lceil \frac{q}{2} \rceil$-dimensional one $\mathcal {U} = C_1' \times C_2' \times \cdots \times C_{\lceil \frac{q}{2} \rceil }'$:

$$\begin{aligned} C_j' = \left\{ \begin{array}{l} C_{\tau (j)} \times C_{\tau (\bar{q}-j+1)},~ 1 \le j \le \lfloor \frac{q}{2} \rfloor \\ C_{\tau (q)}, ~ j=\lceil \frac{q}{2} \rceil ~(\text {if } q \text { is odd}) \end{array}\right. \end{aligned}$$

(34)

where $[\tau (1), \ldots , \tau (q)]$ denotes the ascending order of dimension indexes according to the number of class labels in each class space, $\bar{q}$ is equal to q if q is even and $q-1$ if q is odd. Then, the class vector ${\varvec{y}}_i \in \mathcal {Y}$ which is of nominal type and has length q will be transformed into another nominal class vector ${\varvec{u}}_i \in \mathcal {U}$ with length $\lceil \frac{q}{2} \rceil$, i.e., ${\varvec{u}}_i = \mathcal {P}_{\mathcal {Y}}({\varvec{y}}_i)$, where $\mathcal {P}_{\mathcal {Y}}(\cdot )$ is used to denote the pairwise grou** operation.

Let $s_j$ be the number of class labels in the j-th class space of $\mathcal {U}$, i.e., $C_j' = \{ {c}_1'^{j}, \ldots , {c}_{s_j}'^j \}$, generally $s_j = K_{\tau (j)} \times K_{\tau (\bar{q}-j+1)}$ holds. Besides, if q is odd, $s_{\lceil \frac{q}{2} \rceil } = K_{\tau (q)}$. For ease of numerical calculation, the second step one-hot conversion transforms ${\varvec{u}}_i$ into its one-hot form ${\varvec{v}}_i \in \{0, 1\}^{s}$, where $s=\sum_{j=1}^{\lceil \frac{q}{2}\rceil}s_j,$ i.e., ${\varvec{v}}_i = \Phi _{\mathcal {U}}({\varvec{u}}_i)$. Here, $\Phi _{\mathcal {U}}(\cdot )$ is used to denote the one-hot conversion operation. To be specific, the one-hot form of the j-th item $u_{ij}$ in $\varvec{u}_i$ is a length-$s_j$ vector ${\varvec{v}}_{ij}' \in \{ 0,1 \}^{s_j}$, where the a-th item in ${\varvec{v}}_{ij}'$ is equal to 1 if $u_{ij} = {c}_a'^j$ and 0 otherwise. By concatenating the $\lceil \frac{q}{2} \rceil$ different ${\varvec{v}}_{ij}'$s ($1 \le j \le \lceil \frac{q}{2} \rceil$), the whole one-hot vector ${\varvec{v}}_i$ is obtained.

Until now, note that the transformation is similar to OMLT (cf. Section 3.3.1), except for the additional pairwise grou** operation which makes the resulted binary-valued vector sparser. To obtain a real-valued vector as well as encode the concatenated one-hot vector as an entirety, SLEM generates a random Gaussian matrix $\textbf{A} \in \mathbb {R}^{s' \times s}$, which can transform any length-$s$ vector into a length-$s'$  one. Then the sparse vector ${\varvec{v}}_i$ can be linearly encoded into a length-$s'$ vector ${\varvec{z}}_i = \textbf{A} {\varvec{v}}_i$.

With the obtained real-valued label vector ${\varvec{z}}_i$, the original MDC dataset is transformed into a multi-output regression problem $\widetilde{\mathcal {D}} = \{({\varvec{x}_i, \varvec{z}_i}) \mid 1 \le i \le m \}$. Different from OMLT, here each item in ${\varvec{z}}_i$ contains the labeling information from all original dimensions. To solve the resulted problem, SLEM learns a multi-output regressor $h(\varvec{x}) = \textbf{W}^{\textrm{T}} {\varvec{x}} + {\varvec{b}}$ by optimizing the following formulation:

$$\begin{aligned} \min _{\textbf{W},{\varvec{b}},\hat{\textbf{V}}}~{} & {} \frac{1}{2} \left\| \textbf{W} \right\| _F^2 + \lambda \sum \limits _{i=1}^{m} \big [ \left\| h(\varvec{x}_i) - \varvec{z}_i \right\| _2^2 + \nonumber \\{} & {} \gamma _1 \big ( \left\| h(\varvec{x}_i) - {\textbf{A}} {\hat{\varvec{v}}}_i \right\| _2^2 + \gamma _2 \left\| {\hat{\varvec{v}}}_i - {\varvec{v}}_i \right\| _1 \big ) \big ] \end{aligned}$$

(35)

Here, $\textbf{W} = [\varvec{w}_1, \varvec{w}_2, \ldots , \varvec{w}_{s'}] \in \mathbb {R}^{d \times {s'}}$ and ${\varvec{b}} = [b_1, b_2, \ldots , b_{s'}]^{\textrm{T}}$ are the parameters of regressor h to be determined. $\hat{\textbf{V}} = [{\hat{\varvec{v}}}_1, {\hat{\varvec{v}}}_2, \ldots , {\hat{\varvec{v}}}_m]^{\textrm{T}} \in \mathbb {R}^{m \times s}$ and ${\hat{\varvec{v}}}_i$ is the recovered version of ${\varvec{v}}_i$ based on $h(\varvec{x}_i)$ via $\ell _1$-norm. $\lambda$, $\gamma _1$ and $\gamma _2$ are three parameters to trade-off different items in objective function. This problem can be solved by alternately optimizing the two sets of parameters $\{\textbf{W},{\varvec{b}}\}$ and $\hat{\textbf{V}}$ until convergence. When $\hat{\textbf{V}}$ is fixed, it is equivalent to optimize the following formulation:

$$\begin{aligned} \min _{\textbf{W},{\varvec{b}}}~\frac{1}{2} \left\| \textbf{W} \right\| _F^2{} & {} + \lambda \sum \limits _{i=1}^{m} \big [ \left\| h(\varvec{x}_i) - \varvec{z}_i \right\| _2^2 \nonumber \\{} & {} + \gamma _1 \left\| h(\varvec{x}_i) - {\textbf{A}} {\hat{\varvec{v}}}_i \right\| _2^2 \big ] \end{aligned}$$

(36)

It can be proved that the above problem is further equivalent to optimize the following formulation (cf. Theorem 1 in [67]):

$$\begin{aligned} \min _{\textbf{W},{\varvec{b}}}~\frac{1}{2} \left\| \textbf{W} \right\| _F^2 + \frac{\tilde{\lambda }}{2} \sum \limits _{i=1}^{m} \left\| h(\varvec{x}_i) - \tilde{\varvec{z}}_i \right\| _2^2 \end{aligned}$$

(37)

where $\tilde{\lambda } = 2\lambda (1+\gamma _1)$ and $\tilde{\varvec{z}}_i = \frac{\varvec{z}_i + \gamma _1 {\textbf{A}} {\hat{\varvec{v}}}_i}{1+\gamma _1}$. The above equivalent formulation is a least square problem and has closed-form solution. When $\{\textbf{W},{\varvec{b}}\}$ is fixed, it is equivalent to optimize the following m independent formulation:

$$\begin{aligned} \min _{{\hat{\varvec{v}}}_i}~\left\| h(\varvec{x}_i) - {\textbf{A}} {\hat{\varvec{v}}}_i \right\| _2^2 + \gamma _2 \left\| {\hat{\varvec{v}}}_i - {\varvec{v}}_i \right\| _1,~(1 \le i \le m) \end{aligned}$$

(38)

The above equivalent formulation can be solved by accelerated proximal gradient algorithm which iteratively conducts a variant of soft-thresholding function (For more details, please refer to Algorithm 1 in [67]).

After the model parameters $\{\textbf{W},{\varvec{b}}\}$ are determined, given an unseen instance $\varvec{x}_*$, its encoded vector can be predicted as ${\varvec{z}}_* = h({\varvec{x}}_*)$. Based on ${\varvec{z}}_*$, its final class vector ${\varvec{y}}_*$ can be determined via conducting inverse operations of the three previous cascaded transformations in a reverse order. SLEM implements the inverse of sparse label encoding (denoted by $\mathcal {R}$) by adapting the orthogonal matching pursuit algorithm to consider its specific sparse structure (cf. Algorithm 2 in [67]), i.e., ${\varvec{v}}_* = \mathcal {R}({\varvec{z}}_*)$. For the inverse of one-hot conversion and pairwise grou**, both of them correspond to fixed rules according to multi-dimensional labeling information, i.e., ${\varvec{u}}_* = \Phi _{\mathcal {U}}^{-1}({\varvec{v}}_*)$ and ${\varvec{y}}_* = \mathcal {P}_{\mathcal {Y}}^{-1}({\varvec{u}}_*)$. Algorithm 7 presents the pseudocode of SLEM¹³.

SLEM initiates the entire label space transformation via encoding matrix. Compared with the previous dimension-wise label space transformation strategy, the entire scheme can further alleviate the heterogeneity of class spaces in MDC. The following works ADVAE-Flow [89] and DSOC [90] propose end-to-end manners to conduct label encoding that can better deal with the heterogeneous problem in MDC.

Algorithm 8 KNN feature augmentation for MDC

3.3.3 KNN feature augmentation for MDC

The basic idea of KNN feature augmentation for MDC (KRAM) is to manipulate the feature space by enriching the original feature space with generated augmented features based on kNN techniques [62].

Specifically, by combining the kNN statistics in each dimension, KRAM generates a vector containing labeling information from all dimension. Given any input $\varvec{x}$, let $\mathcal {N}_{k}(\varvec{x}) = \{ i_r \mid 1 \le r \le k \}$ be the index set of its k nearest neighbors identified in training set $\mathcal {D}$. For convenience, it is assumed that the smaller the value of r, the closer the distance between $\varvec{x}$ and ${\varvec{x}}_{i_r}$. Then, an indicating vector ${\varvec{v}}_{ja}^{\varvec{x}} = \left[v_{ja}^{\varvec{x}}(1), v_{ja}^{\varvec{x}}(2), \ldots , v_{ja}^{\varvec{x}}(k)\right]^{\textrm{T}} \in \{0,1\}^k$ can be defined for the k nearest neighbors w.r.t. the a-th class label in the j-th dimension, i.e., $c_a^j$ ($1 \le j \le q$, $1 \le a \le K_j$):

$$\begin{aligned} v_{ja}^{\varvec{x}}(r) = [\![ y_{i_rj} = c_a^j ]\!], ~~(1 \le r \le k, i_r \in \mathcal {N}_k(\varvec{x})) \end{aligned}$$

(39)

where $y_{i_rj}$ denotes the class label of ${\varvec{x}}_{i_r}$ in j-th dimension. The predicate $[\![ {\pi } ]\!]$ returns 1 if $\pi$ holds and 0 otherwise as previously stated. In other words, $v_{ja}^{\varvec{x}}(r) =1$ means that the class label in the j-th dimension of the r-th nearest neighbor ${\varvec{x}}_{i_r}$ for $\varvec{x}$ is $c_a^j$. Then, the number of samples in the k nearest neighbors of $\varvec{x}$ whose class label in the j-th dimension is $c_a^j$ can be computed as follows:

$$\begin{aligned} \delta _{ja}^{\varvec{x}} = \sum \limits _{r=1}^{k} v_{ja}^{\varvec{x}}(r) = {\varvec{1}}_k^{\textrm{T}} {\varvec{v}}_{ja}^{\varvec{x}},~~(1\le a \le K_j, 1 \le j \le q) \end{aligned}$$

(40)

where ${\varvec{1}}_k$ is a length-k column vector of all ones.

After traversing each class label in each dimension, the following length-$\sum _{j=1}^{q}K_j$ vector $\Delta _{\varvec{x}}$ can be obtained for $\varvec{x}$:

$$\begin{aligned} \Delta _{\varvec{x}} ={} & {} [\underbrace{\delta _{11}^{\varvec{x}},\delta _{12}^{\varvec{x}},\ldots ,\delta _{1K_1}^{\varvec{x}}}_\text {The 1st dim.},\underbrace{\delta _{21}^{\varvec{x}},\delta _{22}^{\varvec{x}},\ldots ,\delta _{2K_2}^{\varvec{x}}}_\text {The 2nd dim.}, \nonumber \\{} & {} \ldots , \underbrace{\delta _{q1}^{\varvec{x}},\delta _{q2}^{\varvec{x}},\ldots ,\delta _{qK_q}^{\varvec{x}}}_\text {The qth dim.}]^{\textrm{T}} \end{aligned}$$

(41)

Based on the above newly obtained vector for each training sample, the original MDC training set $\mathcal {D}$ can be transformed into the following new dataset:

$$\begin{aligned} \widetilde{\mathcal {D}}=\{(\tilde{\varvec{x}}_i,{\varvec{y}}_i)\mid 1\le i\le m\} \end{aligned}$$

(42)

Here, $\tilde{\varvec{x}}_i=\left[ {\varvec{x}}_i;{{\varvec{\Delta }}_{{\varvec{x}}_i}}\right] \in \widetilde{\mathcal {X}}$ corresponds to the concatenation of ${\varvec{x}}_i$ and ${{\varvec{\Delta }}_{{\varvec{x}}_i}}$, i.e., the feature augmentation operation. The synthetic feature space $\widetilde{\mathcal {X}}$ corresponds to the Cartesian product between the original feature space (i.e., $\mathcal {X}$) and a $(\sum _{j=1}^q K_j)$-dimensional augmented one. Note that the only difference between $\widetilde{\mathcal {D}}$ and $\mathcal {D}$ is the part of feature vector. In other words, $\widetilde{\mathcal {D}}$ is still an MDC dataset. Moreover, the augmented feature vector ${{\varvec{\Delta }}_{{\varvec{x}}_i}}$ brings additional discriminative information from all dimensions into the feature space which can implicitly consider the dependencies among different dimensions and then should be easier to be solved. Based on the newly obtained dataset $\widetilde{\mathcal {D}}$, an MDC predictive model $f:\widetilde{\mathcal {X}}\mapsto \mathcal {Y}$ can be trained by applying any off-the-shelf MDC training algorithm $\mathfrak {L}$, i.e.,$f$ ↤ $\mathfrak {L}(\widetilde{\mathcal {D}})$.

The augmented feature vector $\Delta _{\varvec{x}}$ in Eq. (41) is based on the standard kNN techniques, where the k nearest neighbors for one instance have the same significance. By introducing a continuous bias to the statistics $\delta _{ja}^{\varvec{x}}$ in Eq. (40), KRAM also defines another version of augmented feature vector based on the weighted kNN techniques. Let ${\varvec{w}} = [1, 1/\sqrt{2}, \ldots , 1/\sqrt{k}]^{\textrm{T}}$ be a weight vector for k nearest neighbors from the closest one to the farthest one, a bias $\zeta _{ja}^{\varvec{x}}$ for $\delta _{ja}^{\varvec{x}}$ in Eq. (40) is defined as follows:

$$\begin{aligned} \zeta _{ja}^{\varvec{x}}=\frac{{\varvec{w}}^{\textrm{T}} \varvec{v}_{ja}^{\varvec{x}} - \min \left( \varvec{v}_{ja}^{\varvec{x}}\right) }{\max \left( \varvec{v}_{ja}^{\varvec{x}}\right) -\min \left( \varvec{v}_{ja}^{\varvec{x}}\right) }(\zeta _{\max }-\zeta _{\min })+\zeta _{\min } \end{aligned}$$

(43)

Here, $\max \left( \varvec{v}_{ja}^{\varvec{x}}\right) = \sum _{r=1}^{ {\varvec{1}}_k^{\textrm{T}} \varvec{v}_{ja}^{\varvec{x}} } w(r)$ and $\min \left( \varvec{v}_{ja}^{\varvec{x}}\right) = \sum _{r=k- {\varvec{1}}_k^{\textrm{T}} \varvec{v}_{ja}^{\varvec{x}} + 1}^{k} w(r)$ represent the possible maximum and minimum of ${\varvec{w}}^{\textrm{T}}{\varvec{v}}_{ja}^{\varvec{x}}$, respectively, where w(r) denotes the r-th item in $\varvec{w}$. $\zeta _{\max }$ and $\zeta _{\min }$ are two hyper-parameters, and $\zeta _{\max } - \zeta _{\min } < 1$ holds. KRAM simply sets $\zeta _{\max }$ to be 0.5 and $\zeta _{\min }$ to be 0. It is easy to know that $\zeta _{\min } \le \zeta _{ja}^{\varvec{x}} \le \zeta _{\max }$. With this bias, the statistics can be modified as follows:

$$\begin{aligned} \delta _{ja}^{\varvec{x}} = {\varvec{1}}_k^{\textrm{T}} {\varvec{v}}_{ja}^{\varvec{x}} + \zeta _{ja}^{\varvec{x}},~~(1\le a \le K_j, 1 \le j \le q) \end{aligned}$$

(44)

Then, another augmented vector $\Delta _{\varvec{x}}$ will be obtained, where the k nearest neighbors for one instance have different significances.

With the MDC model f learned over $\widetilde{\mathcal {D}}$, given an unseen instance ${\varvec{x}}_*$, KRAM firstly computes its augmented feature vector ${\varvec{\Delta }}_{{\varvec{x}}_*}$ similar to training examples, then its predicted class vector ${\varvec{y}}_*$ can be assigned by feeding $\tilde{\varvec{x}}_* = \left[ {\varvec{x}}_*;{\varvec{\Delta }}_{{\varvec{x}}_*}\right]$ into f, i.e., ${\varvec{y}}_* = f(\tilde{\varvec{x}}_*)$. Algorithm 8 presents the pseudocode of KRAM¹⁴.

Fig. 5

Relationships among multi-dimensional classification, multi-label classification and multi-class classification. a Multi-dimensional classification; b multi-label classification (mathematical view); c multi-class classification; d multi-label classification (common assumption). Here, relevant labels are shown in shaded style

KRAM initiates the feature manipulation study [91] for MDC. Although the feature augmentation in KRAM does not explicitly consider class dependencies, useful discriminative information w.r.t. all dimensions can be indeed brought into the feature space which will facilitate the subsequent MDC model induction. The following works LEFA [58] and SFAM [92] improve KRAM from the generation and utilization steps of augmented features, respectively. Specifically, LEFA aims at generating augmented features via deep learning techniques while SFAM aims at synergizing the original features and the augmented features via feature selection. On the other hand, Cambuí et al. [54] aim at extracting lower dimensional representations via autoencoders to deal with the high feature dimensionality problem in MDC while SDeM [93] aims at directly learning a map** matrix to conduct dimensionality reduction for MDC.

4 Related learning settings

As discussed in Section 3.1, MDC can be transformed into a set of or a single multi-class classification problem(s). In addition to this traditional supervised framework, there are also several other learning frameworks that are related to MDC and are often confused with MDC. In this section, we discuss the following learning settings, including multi-label classification, multi-output learning, hierarchical classification, multi-view learning and multiple clustering. Besides, we also discuss semi-supervised multi-dimensional classification, which aims to reduce the labeling cost.

Fig. 6

Two extentions to multi-dimensional classification. a Multi-dimensional multi-label classification; b multi-dimensional partial label classification. Here, relevant labels are shown in shaded style and there is an additional cross for candidate relevant labels

Fig. 7

Multi-output learning and its special case. a Multi-output learning; b ordinal multi-dimensional classification

4.1 Multi-label classification

Multi-label classification [94,95,96,97] deals with the problem where each object is represented by a single instance while associated with a set of binary labels. By considering each label as a dimension, multi-label classification can be regarded as a special case of MDC where the number of class labels in each class space is equal to 2, i.e., $K_1 = K_2 = \ldots = K_q = 2$. As a result, early MDC studies usually use multi-label classification datasets to evaluate their generalization performance [38, 42, 59, 60].

However, there are essential differences in their problem settings. In multi-label classification, it is usually assumed that all labels come from a homogeneous class space, where each label corresponds to the relevance of one concept in the semantic space. Thus, many multi-label studies divide label set into relevant part and irrelevant part based on the label ranking of predicted confidence [98,99,100,101,102]. In MDC, it is assumed that each dimension corresponds to one heterogeneous class space. Thus, the predicted confidence of labels from different dimensions cannot be compared in their value with each other. For example, given an object in Fig. 1, suppose the predicted confidences for class labels square, circle, triangle, white, grey, black, big, small, medium are 0.51, 0.47, 0.02, 0.35, 0.34, 0.31, 0.55, 0.23, 0.22 in turn and we aim to select three class labels as relevant ones. With homogeneous assumption in multi-label classification, the three class labels with the highest confidences will be returned, i.e., square (0.51), circle (0.47) and big (0.55). But with heterogeneous assumption in MDC, square (0.51), white (0.35) and big (0.55) will be returned, each of them has the largest confidence in its corresponding dimension. In fact, this is also the reason that there are many ranking-based evaluation metrics in multi-label classification [103] while only classification-based evaluation metrics in MDC (cf. Section 2.2).

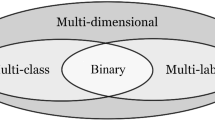
Figure 5 presents an intuitive comparison for MDC, multi-label classification and multi-class classification. Mathematically, by restricting $K_1 = K_2 = \ldots = K_q = 2$ and $q = 1$, MDC will be specialized into multi-label classification and multi-class classification respectively. However, because label ranking is usually utilized in multi-label model induction, Fig. 5d might be more suitable for illustrating the multi-label classification setting, i.e., all labels come from a homogeneous class space. Therefore, multi-label classification should be regarded as a generalized version of multi-class classification by not restricting unique relevant label rather than a special case of MDC. By comparing the difference of Fig. 5a and d, MDC can also be called heterogeneous multi-label classification due to its heterogeneous class spaces as well as multiple relevant labels.

In practical applications, it might be more suitable to use multiple relevant labels to characterize the semantics of MDC objects along one single dimension. Figure 6a illustrates this setting, which is known as multi-dimensional multi-label classification [104] and deals with the problem where a set of class labels in each dimension can be relevant to one object. It can also be regarded as a multi-dimensional extension to multi-label classification. On the other hand, in some scenarios (e.g., crowdsourcing), it is possible to annotate multiple labels for an MDC object in each dimension, but only one is really relevant to the object. Figure 6b illustrates this setting, which is known as multi-dimensional partial label classification [105] and deals with the problem where we only know a candidate label set containing the ground-truth class label in each dimension. It can also be regarded as a multi-dimensional extension to partial label learning [106].

Fig. 8

The patent example. a Hierarchical classification; b multi-dimensional classification

4.2 Multi-output learning

Multi-output learning [107, 108] deals with the problem where each object is represented by a single instance while associated a number of output variables to characterize the multi-dimensional semantics of objects. It is a general term for a class of problems. Specifically, the MDC problem can be regarded as a special case when all output variables are discrete-valued. Moreover, if all output variables are not only discrete-valued but also with an ordinal relationship (e.g., small $\prec$ medium $\prec$ big), then MDC can be further specialized as ordinal multi-dimensional classification [32]. In some literatures, this framework is also termed as multiple ordinal output classification [109, 110], graded multi-label classification [70, 111] or copular ordinal regression [112]. As it is also a classification problem w.r.t. each dimension, publicly available datasets for this problem is also usually used to evaluate MDC models [113]. Figure 7 presents an intuitive comparison for multi-output learning and ordinal multi-dimensional classification.

In addition to MDC and its ordinal version, if all output variables is continuous-valued, multi-output learning will be specialized as multi-output regression [114], which has been widely studied and used as a basic module to solve other machine learning problems [115,116,117,118,119,120]. In Section 3.3.2, SLEM also aims to learn a multi-output regressor by optimizing formulation (35). Besides, there are even some preliminary attempt towards exploring the problem where some output variables are discrete-valued while some other output variables are continuous-valued, which is known as heterogeneous multi-output classification [121] and very challenging to solve.

On the other hand, in a broad sense, multi-output learning can also be regarded as a special case of multi-task learning [122, 123], where the learning problem w.r.t. each output variable corresponds to one task. However, there are also some essential differences. For example, different output variables in multi-output learning share the same feature space while different tasks in multi-task learning do not have to share feature space. Nonetheless, some ideas from multi-task learning can be borrowed to solve multi-output learning problems [124, 125].

4.3 Hierarchical classification

Hierarchical classification [126,127,128] deals with the problem where all class labels are organized in a predefined hierarchical structure. It is similar to MDC in form but very different in nature. Specifically, each dimension in MDC includes all samples while one hierarchical node only includes part of samples belonging to this node class. For example, patents can be hierarchically organized into communication, electricity and electronics in the first level, while in the next level, communication can be further divided into antenna, modulator, telephony, etc., electricity can be further divided into transmission, motive, regulator, etc., and electronics can be further divided into oscillator, amplifier, resistor, etc. [129]. Here, communication, electricity and electronics only include part of patents that belong to the corresponding class. We can also categorize patents from the topic dimensions (with possible classes communication, electricity and electronics), from the type dimension (with possible classes invention, utility model and appearance) and from the region dimension (with possible classes China, USA, Germany, etc.), which corresponds to an MDC problem. Here, each dimension (e.g., topic, type and region) includes all patents.

Figure 8 present the intuitive comparison between hierarchical classification and MDC based on the patent categorization example. As shown in Fig. 8a, for hierarchical classification, the second layer is some specific categories (e.g., communication, electricity and electronics), while the third layer is a further fine classification of these categories respectively. As shown in Fig. 8b, for MDC, the second layer is some abstract characteristics from different dimensions (e.g., topic, type and region), while the third layer is some specific categories w.r.t. these characteristics. In other words, we cannot directly regard the class nodes in the second layer of hierarchical classification as a class space in MDC, nor can we treat the subcategories (i.e., the third layer) belonging to these class nodes as the class labels contained within a class space in MDC. This is because, in hierarchical classification, all class nodes are mutually exclusive except for those with inheritance relationships, where each class node contains different examples. It does not align with the concept of “dimension” in MDC.

4.4 Multi-view learning

Multi-view learning [130,131,132,133] can be regarded as a symmetric learning setting of MDC in feature space. Specifically, a multi-view object often possesses multiple sets of features from different views. Formally, the feature space for multi-view data can be represented by the Cartesian product of different view spaces, i.e., $\mathcal {X} = {V}_1 \times {V}_2 \times \ldots \times {V}_v$. The instance vector of a multi-view object can be represented by ${\varvec{x}} = \left[{\varvec{x}}^1; {\varvec{x}}^2; \ldots ; {\varvec{x}}^v\right]$, where ${\varvec{x}}^l \in \mathcal {V}_l$ denotes the sub-instance vector in the l-th view ($1 \le l \le v$). On the other hand, the output space for MDC data can be represented by the Cartesian product of different class spaces, i.e., $\mathcal {Y} = {C}_1 \times {C}_2 \times \ldots \times {C}_q$. The class vector of an MDC object can be represented by ${\varvec{y}} = [y_1; y_2; \ldots ; y_q]$, where $y_j \in C_j$ denotes the class label in the j-th dimension ($1 \le j \le q$). In other words, in multi-view learning, the properties of one object is described from multiple views in input space, while in MDC, the semantics of one object is characterized from multiple dimensions in output space. Here, it becomes evident that the concepts of view and dimension are symmetrical, originating from the input space and output space, respectively.

Fig. 9

An example of multi-view multi-dimensional classification

Note that multi-view learning is solely concerned with the manner of feature representation and is independent of the form of labeling information. In practical applications, objects can be described from multiple views within the input space and characterized by multiple dimensions within the output space, resulting in multi-view multi-dimensional classification. For example, as depicted in Fig. 9, a movie possesses several feature sets related to its visual, auditory, and subtitle information; each of these feature sets represents a distinct view. On the other hand, its semantics can be characterized along three dimensions, including genre, country, and language. Consequently, by taking into account both the manner of feature representation and the form of labeling information, classifying such a movie object can be formally formalized within the multi-view multi-dimensional classification framework.

4.5 Multiple clustering

As discussed in this paper, the semantic information of MDC data can be modeled from multiple dimensions. It is worth noting that the multi-dimensionality of the data in output space does not stem from the presence of labels, but should be an intrinsic inherent property. That is to say, even without labeling information, there should exist multiple different yet meaningful clusterings if we conduct clustering analysis on MDC data. This problem is known as multiple clustering [134]. Specifically, multiple clustering also needs to analyze the data from multiple dimensions. The difference lies in that MDC is a supervised learning framework, where the data contains labeling information, whereas multiple clustering is an unsupervised learning framework, where the data does not contain labeling information. Thus, multiple clustering can also be regarded as the unsupervised counterpart of MDC.

To generate multiple clusterings, an intuitive strategy is to run the same clustering algorithm multiple times with different parameters or to run different kinds of clustering algorithms. However, the resulting clusterings from such a straightforward approach may be similar because they do not take into account one another. To address this issue, one strategy is to generate multiple clusterings in parallel, ensuring that the results are diverse [135,136,137]. Another strategy is to generate multiple clusterings sequentially, where previous clusterings serve as references to ensure the diversity of the new clustering [138, 139]. Multiple clustering is an ongoing research topic and beyond the scope of this paper. For more recent developments, the comprehensive survey by [134] is recommended, which provides a systematic and thorough discussion of existing multiple clustering algorithms.

4.6 Semi-supervised multi-dimensional classification

Generally, collecting one labeled MDC object should be annotated from multiple dimensions which is rather costly. To deal with this issue, Huang et al. [140] investigate the semi-supervised multi-dimensional classification (SSMDC) learning setting, where the MDC model is learned with a few labeled MDC objects as well as a large number of unlabeled objects. Specifically, in SSMDC, there are a set of labeled MDC samples $\mathcal {D}_l=\{({\varvec{x}}_i,{\varvec{y}}_i)\mid 1\le i\le L\}$ as well as a set of unlabeled samples $\mathcal {D}_u=\{{\varvec{x}}_i\mid L+1\le i\le L+U\}$. Generally, it is assumed that $L \ll U$ holds. The task of SSMDC is to induce an MDC predictive model from $\mathcal {D} = \mathcal {D}_l \cup \mathcal {D}_u$.

The pioneering PLAP algorithm [140] works in progressive label propagation manner. Specifically, PLAP chooses to propagate the labeling information from labeled samples to unlabeled data via the following label propagation equation:

$$\begin{aligned} \textbf{F}(t)=\alpha \textbf{SF}(t-1)+(1-\alpha )\textbf{Y} \end{aligned}$$

(45)

Here, $\textbf{Y}$ is the initial label matrix, $\textbf{F}(t)$ is the propagated label matrix in the t-th round ($t \in \{1, 2, \ldots \}$) and $\alpha \in (0,1)$ is a trade-off parameter to balance their importance. $\textbf{S}= \textbf{D}^{-\frac{1}{2}}\textbf{W} \textbf{D}^{-\frac{1}{2}}$ is the propagation matrix, where $\textbf{D} = diag(d_1,d_2,\dots ,d_{L+U})$ is a diagonal matrix with $d_i=\sum _{j=1}^{L+U} W_{ij}$ and the (i, j)-th item $W_{ij}$ in $\textbf{W}$ denotes the similarity between ${\varvec{x}}_i$ and ${\varvec{x}}_j$ defined as follows:

$$\begin{aligned} W_{ij} = \left\{ \begin{array}{ll} e^{-\frac{\left\| {\varvec{x}}_i-{\varvec{x}}_j \right\| ^2}{2\sigma ^2}}, &{} {\textrm{if}}~i \ne j\\ 0, &{} {\textrm{otherwise}} \end{array} \right. \end{aligned}$$

(46)

where $\sigma$ is the bandwidth parameter. Generally, $\textbf{F}(0)$ is initialized as $\textbf{Y}$ in the first iteration. To consider the dependencies among class spaces, PLAP progressively deals with each dimension with the definition of $\textbf{Y}$ varying depending on the dimension being considered. Specifically, for the first class space $C_1$, the (i, a)-th item $Y_{ia}$ in $\textbf{Y} \in \{ 0,1 \}^{(L+U) \times K_1}$ will be configured as follows:

$$\begin{aligned} Y_{ia} = \left\{ \begin{array}{ll} 1, &{} {\textrm{if}}~(1 \le i \le L) \wedge \left( y_{i1} = c_a^1\right) \\ 0, &{} {\textrm{otherwise}} \end{array} \right. \end{aligned}$$

(47)

In other words, $Y_{ia}$ is set to 1 for the labeled sample $\varvec{x}_i$ (where $1 \le i \le L$) if its class label w.r.t. $C_1$ is $c_a^1$ (that is, $y_{i1} = c_a^1$), and to 0 otherwise. Given $\textbf{Y}$, the corresponding matrix $\textbf{F} \in \mathbb {R}^{(L+U) \times K_1}$ can be obtained by iterating Eq. (45) until convergence. Let $F_{ia}$ be the (i, a)-th item of $\textbf{F}$, the class label $\hat{y}_{i1}$ of the unlabeled sample $\varvec{x}_i$ (where $L+1 \le i \le L+U$) w.r.t. $C_1$ can then be determined using the following rule:

$$\begin{aligned} \hat{y}_{i1} = c_{\hat{a}}^1,~~{\textrm{where}}~\hat{a} = \underset{1 \le a \le K_1}{\arg \max }~ F_{ia} \end{aligned}$$

(48)

Subsequently, for the j-th class space $C_j$ ($j \ge 2$), to model the dependencies among $C_1$, $\ldots$, $C_j$, PLAP considers the first j class spaces as an entirety with the transformation in CP (cf. Fig. 4 for an intuition). Additionally, the prior predictions concerning $C_1$ to $C_{j-1}$ for unlabeled samples are also taken into account to define the current $\textbf{Y}$ in Eq. (45). Let $\phi _j(a_1, \ldots , a_j)$ be some injective function from the Cartesian product $\{1,2,\dots ,K_1\}\times \ldots \times \{1,2,\dots ,K_j\}$ to the set of natural numbers $\{1, 2, \dots , K_1 \times \ldots \times K_j\}$ and we denote $K_{1j} = K_1 \times \ldots \times K_j$ for simplicity, to establish the current $\textbf{Y}$ with size ${N \times K_{1j}}$, the following two cases are considered:

• 1. For labeled sample $\varvec{x}_i$ ($1 \le i \le L$):

  $$\begin{aligned} Y_{i\phi _j(a_1,\ldots ,a_j)} = \left\{ \begin{array}{ll} 1, &{}{\textrm{if}}~{\textrm{CL}}_i^j={\textrm{true}}\\ 0, &{}{\textrm{otherwise}} \end{array}\right. \end{aligned}$$

  (49)

  where ${\textrm{CL}}_i^j \triangleq \left(y_{i1} = c_{a_1}^{1}\right) \wedge \ldots \wedge \left(y_{ij} = c_{a_j}^{j}\right)$. In other words, the corresponding item $Y_{i\phi _j(a_1,\ldots ,a_j)}$ for labeled sample $\varvec{x}_i$ is directly determined by its class labels $y_{i1}$ to $y_{ij}$ w.r.t. $C_1$ to $C_j$ respectively.

• 2. For unlabeled sample $\varvec{x}_i$ ($L+1\le i \le L+U$), the class labels w.r.t. $C_1$ to $C_{j-1}$ have already been predicted while the class label w.r.t. $C_j$ is yet to be determined. Let $\mathcal {N}(\varvec{x}_i)$ be the k nearest neighbors of $\varvec{x}_i$ identified in $\mathcal {D}_l$, and $n_{ia_j}^{j}$ be the number of samples with class label $c_{a_j}^{j}$ w.r.t. $C_j$ in $\mathcal {N}(\varvec{x}_i)$, it follows that $\sum _{a_j=1}^{K_j} n_{ia_j}^{j} = k$. Assuming that $\varvec{x}_i$ has been predicted as $c_{\hat{a}_1}^{1}, \ldots , c_{\hat{a}_{j-1}}^{j-1}$ w.r.t. $C_1$ to $C_{j-1}$, PLAP defines $\textbf{Y}$ as follows:

  $$\begin{aligned} Y_{i\phi _j(a_1,\ldots ,a_j)} = \left\{ \begin{array}{ll} \frac{n_{ia_j}^{j}}{k}, &{}{\textrm{if}}~{\textrm{CU}}_i^j = {\textrm{true}}\\ 0, &{}{\textrm{otherwise}} \end{array}\right. \end{aligned}$$

  (50)

  where ${\textrm{CU}}_i^j \triangleq \left(a_1 = \hat{a}_1\right)\wedge \ldots \wedge \left(a_{j-1} = \hat{a}_{j-1}\right)$ and $1 \le a_j \le K_j$.

Once $\textbf{Y}$ is determined via Eqs. (49) and (50), the corresponding $\textbf{F} \in \mathbb {R}^{N \times K_{1j}}$ can be obtained via iterating Eq. (45) until convergence. For unlabeled sample $\varvec{x}_i$ ($L+1 \le i \le L+U$), its class labels w.r.t. $C_1$ to $C_j$ can be determined as follows:

$$\begin{aligned} \hat{y}_{i1} ={} & {} c_{\hat{a}_1}^1, \ldots , \hat{y}_{ij} = c_{\hat{a}_j}^j, \nonumber \\{} & {} {\textrm{where}}~\left[ \hat{a}_1, \ldots , \hat{a}_j\right] = \phi _j^{-1}(\hat{a}) \nonumber \\{} & {} {\textrm{and}}~\hat{a} = \underset{1 \le a \le K_{1j}}{\arg \max }~F_{ia} \end{aligned}$$

(51)

where $\phi _j^{-1}$ corresponds to the inverse of the injective function $\phi _j$.

PLAP initiates the study for the MDC problem under the semi-supervised learning setting¹⁵. The subsequent work, the DCCC algorithm [141] combines decomposition-based classifier chains (cf. Section 3.2.1) with label propagation to determine the final prediction for unlabeled samples. To date, there have only been these two works on the SSMDC problem, both operating under the closed-world assumption. It is interesting to further explore SSMDC algorithms in open-world assumption [142, 143] where test samples are unavailable to model induction.

5 Conclusion

In this paper, the state-of-the-art of MDC is reviewed in terms of the paradigm, learning algorithms and related learning settings. Specifically, the paradigm presents the fundamental elements for MDC studies, including formal definition of MDC, commonly-used metrics for evaluating MDC models, and publicly available MDC datasets. Then, eight representative MDC algorithms are presented with discussions on their related works. Finally, some related learning settings to MDC are discussed to disambiguate similar concepts and extend the rim of MDC.

Although great progresses on MDC have been made in recent years, there are also many problems to be studied for MDC, at least from the following three aspects:

• At the theory aspect, it is widely acknowledged that modeling class dependencies is the key issue for MDC model induction and existing works mainly validate their effectiveness in dependency modeling via empirical studies, but there is no research on the more essential issues of dependency modeling, including the definition of class dependencies, the existence judgment of class dependencies, and the theoretical analysis of the necessity of class dependency modeling.

• At the methodology aspect, existing works mainly deal with the standard MDC problems, while some specific characteristics in MDC are not considered. For example, the class imbalance problem widely exists in practical applications. Shi et al. [82] make an initial attempt towards class imbalance in MDC from a dimension-wise perspective. However, if regarding the whole output space in MDC as an entirety, more extreme class imbalance problem will appear in general.

• At the data aspect, existing works assume that there are enough labeled MDC samples for model training, while annotating one MDC sample from different dimensions is rather costly. Huang et al. [140] explore the feasibility of learning MDC models with a few labeled samples with the help of large number of unlabeled data. Other solutions for exploiting unlabeled data is also deserved to explore, e.g., active learning [144, 145].