Relax-and-Fix Heuristics Applied to a Real-World Lot Sizing and Scheduling Problem in the Personal Care Consumer Goods Industry

Abstract

This paper addresses an integrated lot sizing and scheduling problem in the industry of consumer goods for personal care, a very competitive market in which good customer service and cost management are crucial in the competition for clients. In this research, a complex operational environment composed of unrelated parallel machines with limited production capacity and sequence-dependent setup times and costs is studied. There is also a limitation in the total storage capacity for finished goods, a characteristic not found in the literature. Backordering is allowed, but it is extremely undesirable. The problem is described through a mixed integer linear programming formulation. Since the problem is NP-hard, relax-and-fix heuristics with hybrid partitioning strategies are investigated. Computational experiments with randomly generated and real-world instances are presented. The results show the efficacy and efficiency of the proposed approaches. Compared to the current solutions used by the company, the best proposed strategies yield results with substantially lower costs, primarily from the reduction in inventory levels and better allocation of production batches on the machines.

1 Introduction

According to the Brazilian Toiletry, Perfumery and Cosmetic Association (ABIHPEC), the Brazilian market for personal care, perfumery, and cosmetics showed growth of $2.2\%$ in 2020 above the $-4.5\%$ of overall industry and $-4.1\%$ of the GDP (Gross Domestic Product) (both heavily affected by the COVID-19 pandemic) and a CAGR (Compound Annual Growth Rate) of $1.7\%$ over the last 10 years compared to a CAGR of $-2.1\%$ for industry overall and $-0.3\%$ for GDP over the same period [1]. Among the factors that have contributed to this accelerated growth are the growing participation of women in the labor market, the frequent releases of new products, the higher productivity achieved by using cutting-edge technology, and, more recently, the essentiality of the segment’s products in combating the COVID-19 pandemic. This segment comprises a large number of small manufacturers and some large companies. In 2020, Brazil held the fourth largest consumer market of this sector in the world, valued at US$ 23.7 billion. Inside this market, the segment studied in this work is the disposable personal care segment, composed of diapers, sanitary pads, toilet paper, towels, and tissues. These products are characterized by (i) frequent consumption by the population, (ii) relatively low cost, and (iii) very similar quality among different brands. Therefore, the processes of production planning, scheduling and control serve important roles for companies to guarantee productivity, cost control, and an adequate customer service level. In most companies, the main responsibility of this activity is to simultaneously analyze several relevant pieces of information, such as the seasonality of the demand, the seasonality of the supply of raw materials, the perishability of the finished products and the raw material, and the manufacturing capacity, to develop a production plan that optimizes the use of productive resources while meeting the demand for manufactured products.

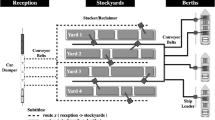
In this work, a case study of a large company in the market of disposable personal care products is performed. The company has factories in southern and southeastern Brazil, and its market is also geographically concentrated in these regions. Its main product categories are diapers, feminine sanitary pads, and toilet paper. These products are manufactured by the company itself, and their demands are predominantly affected by the company’s marketing activities and by the competition. Other products, such as tissue paper, which is commonly utilized in the winter due to a higher frequency of respiratory infections, and disposable napkins and paper towels, which are largely sold during holiday times such as Christmas, Easter, and the New Year, among others, have a strong seasonal demand. The production configuration of the company consists of machines of different models that have been acquired over time as demand was increasing. These machines have performance profiles distinct from each other with regard to efficiency, speed, and cost. Moreover, due to technical constraints, not all products can be manufactured by all machines. Between the production of batches of different products on the same line, machine preparation (setup) is required, which may be as simple and rapid as changing the consuming packing, or complex and slow if it involves a change of raw material or reconfiguration of the parameters of the product, among others. Thus, these setups depend on the product to be produced and on the product that was being produced in the previous batch. The manufactured products are shipped to a limited capacity distribution center located close to the factories. Figure 1 schematically represents the process.

Fig. 1

Schematically representation of the production process

Typical production planning decisions, such as lot sizing and scheduling, significantly influence the results of a company by maximizing the fulfillment of sales orders, correctly adjusting the inventory levels, and incurring proper operating costs. The process of lot sizing consists of determining how much of each product to produce in each period to meet a projected demand under the existing conditions and operational capabilities. On the other hand, scheduling means determining when and in which sequence these lots should be produced to maximize the productive resource efficiency and to meet the deadlines. Inefficiencies in these processes can cause overstocking of finished products, unfulfilled sales orders, loss of perishable material, missed due dates, significant reduction in the productive capacity of the production line, stocks of finished products accumulated in advance, and higher preparation machine costs, among others.

The proposed solution method is a customized relax-and-fix heuristic that decomposes a mixed integer linear programming (MILP) model that represents the entire problem into less complex subproblems that are successively solved. This matheuristic approach is mentioned by Copil et al. [2] as the next generation of solution methods for the MILP models of the lot sizing and scheduling problems. It should be noted that the proposed strategy requires minimal technical knowledge to be applied in situ and opens the possibility that subproblems (which are smaller and therefore simpler) may be solved with established off-the-shelf software. The proposed strategy strikes a balance between market-ready tools, where the firm must adapt to the capabilities of the software, and the development of more elaborate ad hoc solution methodologies such as customized metaheuristics that require hiring specialized teams. Eleven different decomposing approaches are presented. Nine of them are problem-dependent strategies that divide the main problem considering several metrics associated with machines, products, and periods, and two of them are problem-independent strategies. The aim of the study is not only to solve a complex real-world problem, but also to assess in which ways the form of partitioning the problem into simpler subproblems and the sequence in which subproblems are solved affect the performance of the relax-and-fix heuristic.

The rest of this paper is organized as follows. A literature review is presented in Section 2. In Section 3, a MILP formulation of the problem is given. In Section 4, the considered relax-and-fix heuristics are described. In Section 5, numerical experiments with randomly generated instances and real-world instances of the company are conducted. The proposed heuristic methods are compared against a commercial solver applied to the MILP model presented in Section 3, while for the real-world instances, a comparison with the solutions adopted by the company is also presented. Conclusions are given in the last section.

2 Literature Review

In the literature, the integrated lot sizing and scheduling problem with dependent setup times and costs on a single machine (or a single line) is called GLSPST (general lot sizing and scheduling problem with sequence-dependent setup time), while the same problem involving parallel machines is called GLSPPL (general lot sizing and scheduling problem with parallel machines). The GLSP with nonzero minimum lot sizes and without setup times has been proven to be NP-complete by Fleischmann and Meyr [3]. Consequently, the GLSP and the GLSPPL with sequence setup times are also NP-hard [4, 5]. The focused problem can be considered as the GLSPPL with sequence-dependent setup times and costs, nonidentical parallel machines, and specific characteristics of the environment addressed, such as limited warehousing capacity for finished products, machine eligibility constraints, backorder costs, and setup state conservation among adjacent periods. To the knowledge of the authors, few studies have addressed the GLSPPL with all the characteristics of the focused real-world problem.

Due to the relevance of production planning for the industry and its complexity, many authors have addressed the lot sizing and scheduling problem with different characteristics. See classical reviews about the theme in [6-10], and for a recent review see [2]. A brief description of the works that address GLSPPL with specific characteristics is presented below. Differences from the problem considered in this work are highlighted.

Kang et al. [11] treated the GLSPPL considering the minimization of setup and inventory costs using column generation techniques. In this work, the cost of sequence-dependent setups is considered, but setup times are ignored. Clark and Clark [12] studied the GLSPPL, whose objective is the minimization of storage and backordering costs, but without considering setup costs. The proposed mathematical model is based on the premise that the maximum number of setups per period is predetermined. A rolling-horizon method and relax-and-fix heuristics are applied. However, the presented computational results show that only small problems can be solved in a reasonable time. Aiming to minimize production, inventory and setup costs without allowing delivery delays, [5] considered the threshold accepting and simulated annealing metaheuristic in small real instances with identical machines. Beraldi et al. [13] developed rolling-horizon and relax-and-fix heuristics to solve the GLSPPL in the textile and fiberglass industry environment. Unlike the mathematical model developed by Meyr [5], the authors introduced a compact formulation for the case of identical machines considering the setup costs but neglected the setup times.

Józefowska and Zimniak [14] developed a decision support system applied to a Polish company that manufactures plastic pipes and whose production environment is composed of unrelated parallel machines. This system is based on a multi-objective model that includes among its criteria the maximization of the machine utilization and the minimization of the deviation between the production schedule and the S &OP (Sales and Operations Plan) and the amount of products below the required level of safety stock. The model is solved using a genetic algorithm after having its solution space reduced by adding restrictions suggested by experienced planners. Mateus et al. [15] approached the lot sizing and scheduling problem by considering a refractory brick factory with different machines in parallel. Unlike the problem addressed in this work, the authors did not consider setup carryover, i.e., when the preparation of the machines is not maintained from one period to the next. The proposed iterative solution method is composed of two modules: the first solves the problem of lot sizing considering aggregate capacity and estimated setup times, while the second searches for a feasible sequencing for pre-sized lots through a GRASP metaheuristic. Meyr and Mann [16] dealt with the GLSPPL composed of heterogeneous parallel machines with the objective of minimizing inventory and sequence-dependent setup and production costs without backlogging. The authors proposed a heuristic that iteratively decomposes the multiline problem into a series of single-line subproblems, which can be easily solved by the heuristic TADR proposed by Meyr [4]. Two strategies for decomposing the problem into subproblems are proposed: (i) a strategy based on priority rules and (ii) another strategy based on aggregating the original problem, solving the aggregate problem, and disaggregating the results to define the demand and initial inventory for each line. ** unit (SKU) must be within specified limits at the end of each period, while each MTO SKU must be produced within its specified time frame. The objective is to maximize the total amount of production in a given planning horizon considering sequence-dependent setup times; the setup costs are not considered. The authors propose a two-phase procedure. First, a MIP model in which the setup times are considered independently of the sequence is formulated and solved. Next, a one-pass heuristic is applied to search for setup time savings by reordering the products assigned by the MIP model to each machine in each period. An overview of simultaneous lot sizing and scheduling involving secondary resources can be found in [23].

3 Mathematical Model

In the GLSPPL, n types of products are manufactured on a shop floor composed of m different machines over a horizon divided into T time periods. In a period t (the time interval that extends from instant $t-1$ to instant t), a machine can produce more than one type of product, provided its time availability is not exceeded. Machines have different production rates and efficiency levels. Some machines, due to their manufacturer, model, or preservation status, can achieve a higher production speed with lower scrap rates than others. Consequently, the production time $p_{i \ell }$ and the production cost $c^P_{i \ell }$ to produce product i on machine $\ell$ depend on the product and the machine. Furthermore, due to technical constraints, not all products can be manufactured by all machines. Between production batches of different types of products, it is necessary to prepare the machine and to set the correct product parameters, which generally generate loss of material. These setup times $e_{i j \ell }$ and, consequently, their respective costs $c^S_{ij\ell }$, are sequence dependent. Preemption is not permitted. The demand $d_{it}$ of each product i at the end of period t is dynamic and deterministic, i.e., it is known and varies over time. Backordering is allowed, but each backordered unit of product i is penalized by $g_i$ per period of delay. Finished goods are transferred from the factory to a centralized distribution center with limited warehousing capacity $C^W$. Each stored unit of product i costs an inventory cost $h_i$ per period. In the considered problem, in addition to defining the quantities of each product to be produced and the production sequence, the solution determines the machine by which each batch is manufactured to minimize the sum of the costs of inventory, setup, production, and backordering.

The MILP formulation presented in the current section is based on the MILP formulation introduced in [5], which does not consider the allowance of backorders, machine eligibility constraints, or the limited capacity of warehousing. In the formulation, many products can be produced by a machine in a certain period of time. The machine availability is consumed by the time necessary to set up the machine and to produce the lot. The setup time and cost depend on the sequence of products that are produced by the machine. The planning horizon is divided into T periods. Within each period t, each machine $\ell$ has $w_{\ell t}$ variable-length subperiods. A machine can produce a single type of product within each subperiod, and the duration of the subperiod is given by the duration of the production of the lot that is being produced. There may be subperiods with zero length, even though the machine is set up to produce some product. The division into subperiods determines the sequence of the jobs on each machine and defines the associated setup times and costs.

To present the proposed model, we introduce the following notation:

Main constants:

m::

number of machines,

n::

number of products,

T::

time horizon (assumed to start at 0).

Indexes:

i, j::

products,

$\ell$::

machines,

t::

periods (a period t corresponds to the time interval between instants $t-1$ and t),

s::

subperiods.

Sets:

$\mathcal{I} = \{ 1, \dots , n\}$::

products,

$\mathcal{L} = \{ 1, \dots , m\}$::

machines,

$\mathcal{I}_{\ell } \subseteq \mathcal{I}$::

products that can be produced by machine $\ell$ ($\ell \in \mathcal{L}$),

$\mathcal{L}_i \subseteq \mathcal{L}$::

machines that can produce product i ($i \in \mathcal{I}$),

$\mathcal{T} = \{ 1, \dots , T\}$::

periods,

$\mathcal{S}_{\ell } = \{ 1, \dots , W_{\ell } \}$::

subperiods of machine $\ell$ ($\ell \in \mathcal{L}$), where $w_{\ell t}$ is the number of subperiods of machine $\ell$ within period t ($\ell \in \mathcal{L}$, $t \in \mathcal{T}$) and $W_{\ell } = \sum _{t \in \mathcal{T}} w_{\ell t}$ ($\ell \in \mathcal{L}$),

$\mathcal{S}_{\ell t} = \{ s \in S_{\ell } \; | \; \bar{w}_{\ell t} + 1 \le s \le \bar{w}_{\ell t} + w_{\ell t}\}$::

subperiods of machine $\ell$ within period t ($\ell \in \mathcal{L}$, $t \in \mathcal{T}$), where $\bar{w}_{\ell t} = 0$ for $t=1$ and $\bar{w}_{\ell t} = \bar{w}_{\ell ,t-1} + w_{\ell ,t-1}$ for $t = 2,\dots ,T$.

Parameters:

$C^W$::

capacity of warehousing,

$C^P_{\ell t}$::

amount of time machine $\ell$ is available (for production and setup) within period t ($\ell \in \mathcal{L}, t \in \mathcal{T}$),

$d_{it}$::

demand for product i at the end of period t, i.e., at instant t ($i \in \mathcal{I}$, $t \in \mathcal{T}$),

$h_i$::

inventory cost per period of a unit of product i ($i \in \mathcal{I}$),

$g_i$::

backordering cost per period of a unit of product i ($i \in \mathcal{I}$),

$p_{i\ell }$::

time required to produce a unit of product i in machine $\ell$ ($\ell \in \mathcal{L}$, $i \in \mathcal{I}_{\ell}$),

$c^P_{i\ell }$::

cost of producing a unit of product i in machine $\ell$ ($\ell \in \mathcal{L}$, $i \in \mathcal{I}_{\ell }$),

$q^{\textrm{lb}}_{i\ell }$::

minimum lot of product i that can be produced in machine $\ell$ ($\ell \in \mathcal{L}$, $i \in \mathcal{I}_{\ell }$),

$e_{ij\ell }$::

setup time required to produce product j immediately after i in machine $\ell$ ($\ell \in \mathcal{L}$, $i, j \in \mathcal{I}_{\ell }$),

$c^S_{ij\ell }$::

cost of the setup required to produce product j immediately after i in machine $\ell$ ($\ell \in \mathcal{L}$, $i, j \in \mathcal{I}_{\ell }$),

$I_{i0}^+$::

inventory (quantity) of product i at instant $t=0$ ($i \in \mathcal{I}$),

$I_{i0}^-$::

backordering (quantity) of product i at instant $t=0$ ($i \in \mathcal{I}$),

$x_{i\ell 0}$::

1, if machine $\ell$ is prepared to produce product i at instant $t=0$; 0, otherwise ($\ell \in \mathcal{L}$, $i \in \mathcal{I}_{\ell }$).

Variables:

$q_{i\ell s}$::

quantity of product i produced in machine $\ell$ within subperiod s ($\ell \in \mathcal{L}$, $s \in S_{\ell }$, $i \in \mathcal{I}_{\ell }$),

$x_{i\ell s}$::

1, if machine $\ell$ is prepared to produce product i at the beginning of subperiod s (i.e., at instant $s-1$); 0, otherwise ($\ell \in \mathcal{L}$, $s \in S_{\ell }$, $i \in \mathcal{I}_{\ell }$),

$y_{ij\ell s}$::

1, if the setup required to produce product j immediately after i in machine $\ell$ occurs within subperiod s, i.e., between instants $s-1$ and s; 0, otherwise ($\ell \in \mathcal{L}$, $s \in S_{\ell }$, $i, j \in \mathcal{I}_{\ell }$),

$I_{it}^+$::

inventory (quantity) of product i at the end of period t, i.e., at instant t ($i \in \mathcal{I}$, $t \in \mathcal{T}$),

$I_{it}^-$::

backordering (quantity) of product i at the end of period t, i.e., at instant t ($i \in \mathcal{I}$, $t \in \mathcal{T}$).

The proposed mathematical formulation is presented below:

$$\begin{aligned} \begin{aligned}&\text{ Minimize } \\ \sum _{i \in \mathcal{I}} \sum _{t \in \mathcal{T}} h_i \, I_{it}^+ + \sum _{i \in \mathcal{I}} \sum _{t \in \mathcal{T}} g_i \, I^-_{it} +&\sum _{\ell \in \mathcal{L}} \sum _{i \in \mathcal{I}_{\ell }} \sum _{j \in \mathcal{I}_{\ell }} \sum _{s \in S_{\ell }} c^S_{i j \ell }\, y_{i j \ell s} + \sum _{i \in \mathcal{I}} \sum _{\ell \in \mathcal{L}_i} \sum _{s \in S_{\ell }} c^P_{i \ell }\, q_{i\ell s} \\&\text{ subject } \text{ to } \quad \end{aligned} \end{aligned}$$

(1)

$$\begin{aligned} I^+_{i, t- 1} - I^-_{i, t-1} + \sum _{\ell \in \mathcal{L}_i} \sum _{s \in S_{\ell t}} q_{i\ell s} - I^+_{it} + I^-_{it} = d_{it}, \quad i \in \mathcal{I}, \; t \in \mathcal{T}, \end{aligned}$$

(2)

$$\begin{aligned} \sum _{i \in \mathcal{I}} I^+_{it} \le C^W, \quad t \in \mathcal{T}, \end{aligned}$$

(3)

$$\begin{aligned} \sum _{i \in \mathcal{I}_{\ell }} \sum _{s \in S_{\ell t}} \left( p_{i\ell }\, q_{i\ell s} + \sum _{j \in \mathcal{I}_{\ell }} e_{ij\ell } \, y_{ij\ell s}\right) \le C^P_{\ell t}, \quad \ell \in \mathcal{L}, \; t \in \mathcal{T}, \end{aligned}$$

(4)

$$\begin{aligned} p_{i\ell } \, q_{i\ell s} \le C^P_{\ell t} \, x_{i\ell s}, \quad \ell \in \mathcal{L}, \; t \in \mathcal{T}, \; s \in S_{\ell t}, \; i \in \mathcal{I}_{\ell } \end{aligned}$$

(5)

$$\begin{aligned} q_{i\ell s} \ge q^{\textrm{lb}}_{i\ell }\, (x_{i\ell s} - x_{i,\ell ,s-1}), \quad \ell \in \mathcal{L}, \; t \in \mathcal{T}, \; s \in S_{\ell t}, \; i \in \mathcal{I}_{\ell } \end{aligned}$$

(6)

$$\begin{aligned} \sum _{i \in \mathcal{I}_{\ell }} x_{i\ell s} = 1, \quad \ell \in \mathcal{L}, \; s \in S_{\ell }, \end{aligned}$$

(7)

$$\begin{aligned} y_{ij\ell s} \ge x_{i\ell ,s-1} + x_{j\ell s} - 1, \quad \ell \in \mathcal{L}, \; s \in S_{\ell }, \; i,j \in \mathcal{I}_{\ell } \end{aligned}$$

(8)

$$\begin{aligned} x_{i\ell s} \in \{0,1\}, \quad \ell \in \mathcal{L}, \; s \in S_{\ell }, \; i \in \mathcal{I}_{\ell } \end{aligned}$$

(9)

$$\begin{aligned} q_{i\ell s} \ge 0, \quad \ell \in \mathcal{L}, \; s \in S_{\ell }, \; i \in \mathcal{I}_{\ell } \end{aligned}$$

(10)

$$\begin{aligned} y_{ij\ell s} \ge 0, \quad \ell \in \mathcal{L}, \; s \in S_{\ell }, \; i,j \in \mathcal{I}_{\ell } \end{aligned}$$

(11)

$$\begin{aligned} I^+_{it}, \, I^-_{it} \ge 0, \quad i \in \mathcal{I}, \; t \in \mathcal{T}. \end{aligned}$$

(12)

Objective function (1) corresponds to the sum of the costs of inventory, backordering, setup, and production. Constraints (2) define inventory and backordering conservation flow, i.e., the relations between inventory, backordering, demand, and produced quantities. Constraints (3) determine that the total amount of inventory cannot exceed the warehousing capacity of the distribution center. In the problem under consideration, the existing storage capacity cannot be increased or violated. (If desired, it would be possible to consider, in the objective function, an additional cost associated with exceeding the current capacity.) Constraints (4) guarantee that the sum of the production time and setup time of each machine within each period does not exceed the corresponding machine’s availability. Constraints (5) ensure that machine $\ell$ produces product i within subperiod s only if the machine has been previously configured for this purpose. Constraints (6) impose a minimum lot size restriction. Constraints (7) determine that, for every machine, within every machine’s subperiod, a single product can be produced. Constraints (8) indicate that if the machine $\ell$ switch from producing product i to producing product j occurs within subperiod s, then the corresponding setup must be accomplished over the course of subperiod s. Constraints (9, 10, 11 and 12) determine the variables’ domain. Note that it is not necessary to impose variables $y_{i j \ell s}$ to be binary because they naturally assume values in $\{0,1\}$ at an optimal solution. This is because constraints (8) restrict them to be larger than or equal to $-1$, 0, or 1, while constraints (11) inhibit the possibility of the variables being negative. The minimization of the objective function forces them to assume binary values at the optimal solution.

4 Relax-and-Fix Heuristics

The main idea of the relax-and-fix (RF) heuristic [24] for solving a MILP problem is to partition the set X of integer variables into K subsets $X_1,\dots ,X_K$ and to solve a sequence of K smaller MILP problems. In the kth subproblem, the variables in $X_k$ are restricted to integers, while the integrality of the variables in $X_{k+1} \cup \dots \cup X_K$ is relaxed and the variables in $X_1 \cup \dots \cup X_{k-1}$ are already fixed; see Fig. 2.

Fig. 2

Relax-and-fix algorithm working structure. In the second subproblem, $\hat{x}_i^1$, $i \in X_1$, correspond to the optimal values found when solving the first subproblem

Model (1–12), which will be named “Model $\mathcal{M}$” from now on, needs to be modified to be used within the context of an RF-based heuristic. Let $X=\{ (i,\ell ,s) \; | \; \ell \in \mathcal{L}, \; s \in S_{\ell }, \; i \in \mathcal{I}_{\ell } \}$ be the set of all valid indices’ 3-uples of variables $x_{i \ell s}$. The RF-based heuristic relies on the partition of the set X into K subsets $X_k$ ($k=1,\dots ,K$) that verify $\cup _{k=1}^K X_k = X$ and $X_{k_1} \cap X_{k_2} = \emptyset$ for all $k_1 \ne k_2$. Let Model $\mathcal{M}_1$ be defined as Model $\mathcal{M}$, in which constraint (9) is substituted with

$$\begin{aligned} \begin{array}{rl} x_{i \ell s} \in \{0,1\}, &{} (i, \ell , s) \in X_1,\\ 0 \le x_{i\ell s} \le 1, &{} (i,\ell , s) \in \cup _{w=2}^K X_w. \end{array} \end{aligned}$$

(13)

We can now define Model $\mathcal{M}_k$, for $k=2,\dots ,K$, as Model $\mathcal{M}$ in which constraint (9) is substituted with

$$\begin{aligned} x_{i \ell s} = \hat{x}_{i \ell s}^w, \quad (i, \ell , s) \in X_w \text{ for } w=1,\dots ,k-1, \end{aligned}$$

(14)

$$\begin{aligned} x_{i \ell s} \in \{0,1\}, \quad (i, \ell , s) \in X_k, \end{aligned}$$

(15)

$$\begin{aligned} 0 \le x_{i\ell s} \le 1, \quad (i,\ell , s) \in \cup _{w=k+1}^K X_w, \end{aligned}$$

(16)

where in (14), $\hat{x}_{i \ell s}^w$ for $(i, \ell , s) \in X_w$ correspond to the optimal values obtained when solving Models $\mathcal{M}_w$ for $w=1,\dots ,k-1$. This expresses the fact that, in Model $\mathcal{M}_k$, variables $x_{i \ell s}$ with $(i, \ell , s) \in \cup _{w=1}^{k-1} X_w$ are fixed, variables $x_{i \ell s}$ with $(i, \ell , s) \in X_k$ preserve their integrality constraint, and variables $x_{i \ell s}$ with $(i, \ell , s) \in \cup _{w=k+1}^{K} X_w$ are variables whose integrality constraint is relaxed. Note that in Model $\mathcal{M}$, constraint (9), which states that $x_{i \ell s} \in \{0,1\}$ for all $(i, \ell , s) \in X$, implies that all variables $y_{i j \ell s}$, for all $\ell \in \mathcal{L}$, $\in S_{\ell }$, $i, j \in \mathcal{I}_{\ell }$, assume binary values at an optimal solution. On the other hand, a different relation holds in Model $\mathcal{M}_k$ ($k=1,\dots ,K$). Due to (8), a variable $y_{i j \ell s}$ is guaranteed to assume binary values in an optimal solution of Model $\mathcal{M}_k$ only if $(i, \ell , s-1)$ and $(j, \ell , s) \in X_k$.

The key feature of an RF-based heuristic is the determination of the number of subproblems K and the sets $X_1, \dots , X_K$. Problem-dependent and problem-independent strategies will be considered. The problem-dependent strategies divide variables $x_{i \ell s}$ considering the dimensions related to machine, product, and period, and they are based on several metrics associated with machines, products, and periods that we now describe. We define the demand $d_i$ of a product i as

$$\begin{aligned} d_i = \sum _{t \in \mathcal{T}} d_{it}; \end{aligned}$$

(17)

and the flexibility $f_i$ of a product i as the number of machines that can produce it, i.e.,

$$\begin{aligned} f_i = | \mathcal{L}_i | \end{aligned}$$

(18)

for all $i \in \mathcal{I}$. In addition, inspired by Vogel’s approximation method for the transportation problem [25, 26]), we define the discrepancy $a_i$ of a product i as the difference between its two smallest processing times, given by

$$\begin{aligned} a_i = p_{i \hat{\ell }_2} - p_{i \hat{\ell }_1}, \; \hat{\ell }_1 = \textrm{argmin}_{\ell \in \mathcal{L}_{i}} \{ p_{i\ell } \}, \; \text{ and } \hat{\ell }_2 = \textrm{argmin}_{\ell \in \mathcal{L}_{i} \setminus \{\hat{\ell }_1\}} \{ p_{i\ell } \}. \end{aligned}$$

(19)

Following [18], we consider a machine to be critical if it is able, and thus it potentially will need to process products with low flexibility. Therefore, we define the criticality $\omega _\ell$ of a machine $\ell$ as

$$\begin{aligned} \omega _\ell = m - \min _{i \in \mathcal{I}_\ell } \{ f_i \} \end{aligned}$$

(20)

for all $\ell \in \mathcal{L}$. We also associate with a machine $\ell$ a metric of efficiency $\varepsilon _\ell$, given by the sum of the machine’s average processing times and costs, i.e.,

$$\begin{aligned} \varepsilon _\ell = \frac{1}{| \mathcal{I}_\ell |} ( \sum _{{i \in \mathcal I}_\ell } p_{i\ell } + c_{i\ell }^P ) \end{aligned}$$

(21)

for all $\ell \in \mathcal{L}$. Finally, for a period $t \in \mathcal{T}$, we define its overall demand $\delta _t$ as

$$\begin{aligned} \delta _t = \sum _{i \in \mathcal{I}} d_{it}. \end{aligned}$$

(22)

As a whole, nine different problem-dependent and two problem-independent partition strategies are considered. Each strategy consists of a way of sorting the 3-uples of indices $(i,\ell ,s) \in X$, where X is the set of valid 3-uples of the variables $x_{i \ell s}$. After sorting, the first $\lfloor |X|/K \rfloor$ variables constitute the set $X_1$, the next $\lfloor |X|/K \rfloor$ variables constitute the set $X_2$, and so on. If |X| is not a multiple of K, then we have that $K \lfloor |X| / K \rfloor < |X|$. Therefore, in the first $r = |X| - K \lfloor |X| / K \rfloor$ subsets, we consider $\lceil \cdot \rceil$ instead of $\lfloor \cdot \rfloor$ for the cardinality of $X_1, \dots , X_r$. In most strategies, the suggested order does not imply a total order of the 3-uples. Therefore, tie-breaking criteria play an important role in the strategies. In the suggested strategies, the tie-breaking criterion will always consist of applying a second strategy. Thus, the strategies are intrinsically hybrid. As a second tie-breaking rule, the lexicographic order of the index 3-uples is used. The description of each strategy follows:

• Time-dimension-based strategies:

  • (S1) Chronological time: Given $(i, \ell , s) \in X$, we have that $s \in \mathcal{S}_{\ell t}$ for some $t \in \mathcal{T}$. 3-uples are sorted in increasing lexicographical order of (t, s), where t is the period t to which subperiod s corresponds.

  • (S2) Periods with larger demand first: The same as (S1), but 3-uples $(i, \ell , s) \in X$ are sorted in decreasing order of $\delta _t$ (instead of increasing order of t), where $\delta _t$ is the demand of period t given by (22).

• Product-dimension-based strategies:

  • (S3) Most demanded products first: 3-uples $(i, \ell , s) \in X$ are sorted in decreasing order of the item demands $d_i$ given by (17).

  • (S4) Less demanded products first: The same as (S3) but in increasing order.

  • (S5) Less flexible products first: 3-uples $(i, \ell , s) \in X$ are sorted in increasing order of the item flexibility $f_i$ given by (18).

  • (S6) First, the products with the largest discrepancy between the two shortest production times: 3-uples $(i, \ell , s) \in X$ are sorted in decreasing order of the item discrepancy $a_i$ given by (19).

• Machine-dimension-based strategies:

  • (S7) Less efficient machines first: 3-uples $(i, \ell , s) \in X$ are sorted in increasing order of the machine efficiency $\varepsilon _{\ell }$ given by (21).

  • (S8) More efficient machines first: The same as (S7) but in decreasing order.

  • (S9) More critical machines first: 3-uples $(i, \ell , s) \in X$ are sorted in decreasing order of the machine criticality $\omega _\ell$ given by (20).

• Problem-independent strategies:

  • (S10) More fractional variables first: In this strategy, we first solve a linear programming (LP) problem that corresponds to Model $\mathcal{M}$ in which the constraint $x_{i \ell s} \in \{0,1\}$ is relaxed to $0 \le x_{i \ell s} \le 1$ for all $(i,\ell ,s) \in X$. Let $\hat{x}_{i \ell s}^0$, for $(i,\ell ,s) \in X$, be the optimal solution of the LP problem. For each variable $x_{i \ell s}$ for $(i,\ell ,s) \in X$, we compute the “distance to integrality” given by

    $$\begin{aligned} d_{i \ell s}^0 = \min \{ \hat{x}_{i \ell s}^0, 1 - \hat{x}_{i \ell s}^0\}. \end{aligned}$$

    3-uples $(i, \ell , s) \in X$ are sorted in decreasing order of their distance to integrality $d_{i \ell s}^0$. In fact, there is no need to sort all 3-uples since, to construct $X_1$, only the $\lfloor |X|/K \rfloor$ or $\lceil |X|/K \rceil$ 3-uples with the largest $d_{i \ell s}^0$ are required. In general, after having solved the kth subproblem ($k<K$), distances $d_{i \ell s}^k= \min \{ \hat{x}_{i \ell s}^k, 1 - \hat{x}_{i \ell s}^k\}$ for $(i,\ell ,s) \in X \setminus \cup _{w=1}^k X_w$ are computed, where $\hat{x}_{i \ell s}^k$ is the optimal solution of the kth subproblem, and the $\lfloor |X|/K \rfloor$ or $\lceil |X|/K \rceil$ 3-uples with the largest $d_{i \ell s}^k$ are selected to constitute $X_{k+1}$.

  • (S11) More influential variables first: In this strategy, variables with more “influence” in the objective function are considered first. This “influence” could be directly related to the cost associated with the variable in the objective function, and this is the most direct interpretation of this rule. However, in the problem at hand, variables $x_{i \ell s}$ with $(i,\ell ,s) \in X$ do not appear in the objective function. However, their values influence the value of variables $q_{i \ell s}$ and $y_{ij\ell s}$. Thus, the influence $\alpha _{i \ell s}$ of variable $x_{i \ell s}$ is defined as

    $$\begin{aligned} \alpha _{i \ell s} = ( \sum _{j \in \mathcal{I}_{\ell }} c_{ij\ell }^S ) + c_{i \ell }^P. \end{aligned}$$

    Note that, in fact, $\alpha _{i \ell s}$ does not depend on s and, therefore, variables $x_{i \ell s_1}$ and $x_{i \ell s_2}$ with $s_1 \ne s_2$ have the same influence measure. Therefore, in the particular problem at hand, this problem-independent strategy depends on the products and the machines. More specifically, products that take a long time to process and/or demand a time-consuming machine preparation after production are thought to be more influential.

Note that strategy (S10) is a dynamic strategy that differs from all other strategies because set $X_k$ is determined after having solved subproblems from 1 to $k-1$, while other strategies determine all subsets $X_1, \dots , X_K$ a priori. Moreover, strategy (S10) requires solving an LP problem first. In the present work, we consider hybrid strategies that consist of applying a problem-dependent strategy between (S1) and (S9), using (S10) or (S11) as the first tie-breaking rule and the lexicographic order in the 3-uples $(i, \ell , s) \in X$ as the second tie-breaking rule. (Hybrid strategies that combined two problem-dependent strategies were also evaluated numerically, but they showed marginal benefits in relation to those presented in this paper.)

5 Numerical Experiments

In this section, we evaluate the performance of the partition strategies described in the previous section. In the first set of experiments, strategies are evaluated with respect to a set of randomly generated instances. In a second experiment, selected strategies are applied to a set of ten real-world instances of the industry of personal care products. The section ends with a basic sensitivity analysis regarding the storage capacity restriction of the warehouses. The experiments were carried out with an Intel Xeon X5690 3.47 GHz machine with 64 GB of RAM. The RF algorithms and the formulations were solved using CPLEX 12.10.0 using default parameters with the concert library and C++ programming language. The code was compiled using the gcc 6.3.0 compiler with Code::Blocks 16.01 IDE. Benchmark instances and code are available at https://github.com/kennedy94/GLSPPL-RF.

5.1 Experiments with Randomly Generated Instances

The benchmark test suite is composed of 50 randomly generated instances inspired by the production environment of the target industry. All instances have a planning horizon composed of 16 time periods divided into 7 subperiods each. As each period corresponds to 1 week, the planning horizon comprises approximately 4 months. (This does not mean that each subperiod corresponds to 1 day. This means that a machine can produce at most seven different products in a period of 1 week. The subperiods correspond to the production of different products on the machine and are of varying duration.)

Five groups of instances were considered (A, B, C, D and E), and ten different random instances were generated within each of the groups, with a total of 50 instances. The random generation used either discrete or continuous uniform distributions, depending on the nature of each parameter. The number of machines m for groups A, B, C, D, and E is 2, 3, 4, 5, and 7, respectively, while the number of products n for groups A, B, C, D, and E is 8, 12, 16, 20, and 28, respectively. It is considered that the machines are not ready for the production of any item at the beginning of the planning horizon, i.e., $x_{i \ell 0}=0$ for all $i \in \mathcal{I}$ and $\ell \in \mathcal{L}_i$. Table 1 shows details of the random generation of all instance parameters. It should be noted that the random instances were generated from real-world data. In the table, $\bar{e}$ is the average of the setup times $e_{ij\ell }$ for $\ell \in \mathcal{L}$ and $i,j \in \mathcal{I}_\ell$, and $d_t$ (for $t \in \mathcal{T}$) corresponds to an aggregated period demand. For each item $i \in \mathcal{I}$, a proportion $d_{i}^p \in [0.05, 0.9]$ is randomly generated (independent of t), and $d_{it}$ is defined as $d_{it} = d_t \; d_i^p / ( \sum _{i \in \mathcal{I}} d_i^p )$. The production and setup time intervals for each group were obtained from the average times and standard deviations provided by the company. The range for the minimum lot $q_{i\ell }^{\textrm{lb}}$ of product i on machine $\ell$ relative to each group was calculated based on the average and the standard deviation, informed by the industrial area of the company, of the minimum feasible quantity to be produced with productivity and material loss within the required standards. In fact, the average and standard deviation were reported for each group in working shifts $\hat{q}^{\textrm{lb}}$ and transformed into units of products $q_{i\ell }^{\textrm{lb}}$ considering the processing times $p_{i\ell }$ and the fact that each working shift corresponds to 8 h of labor, i.e., $q_{i\ell }^{\textrm{lb}} = 8 \; \hat{q}^{\textrm{lb}} / p_{i\ell }$. Production costs $c^P_{i \ell }$ (for $i \in \mathcal {I}$ and $\ell \in \mathcal {L}_i$) are random with a continuous uniform distribution within the range given in the table. However, they are then redefined as $c^P_{i \ell } - c^P_{i \xi _i}$, where $\xi _i = \textrm{argmin}_{\ell \in \mathcal{L}_i} \{ c^P_{i \ell } \}$ corresponds to the most efficient machine that produces item i (for $i \in \mathcal {I}$). The ranges for the amounts of products in stock and backordered products at the beginning of the time horizon were calculated using averages and standard deviations based on historical data provided by the company. The last line of each group displays average values. Table 2 shows detailed information about the generated instances. In the table, columns IV, CV, and CO correspond to the numbers of integer variables, continuous variables, and constraints of Model $\mathcal{M}$, respectively.

Table 1 Detailed information of the random generation of instances’ parameters

Table 2 Detailed information of benchmark random instances

Initially, to decide which of the problem-independent strategies would be used as the tie-breaking rule, we ran strategies S10 and S11 while varying $K \in {1,2,\dots ,10}$. The two rows at the bottom of Table 3 show the results. In the table, the results obtained with $K \ge 2$ are compared with the result obtained with $K=1$, which simply corresponds to solving Model $\mathcal{M}$ using CPLEX. The results appear separated by group and refer to the 10 instances of the group solved with 9 values of $K \in \{2,\dots ,10\}$. Under the heading $(W,G(\%))$ is displayed for how many, out of the 90 cases, the relax-and-fix strategy found a better result (W stands for “win”) than CPLEX and what the average gap was in these cases ($G(\%)$ stands for “average gap in percentage”). Under the heading $(L,G(\%))$ appears for how many of the 90 cases the relax-and-fix strategy performed worse (L stands for “lost”) than CPLEX and the average gap in these cases. Since there were no ties, if the number of wins and losses does not add up to 90, it is because for some instances and values of K, relax-and-fix could not find a feasible solution within the running time limit. The last column of the table shows the average gap considering the 50 instances and the 9 tested values of K. The results show that strategy S11 obtained better results than strategy S10 and, for this reason, it will be used as a tie-breaker for all the other strategies that depend on the problem. The performance of strategies S1 to S9, using S11 as the tie-breaker strategy, is shown at the top of Table 3. At this point, it is important to mention that for both CPLEX and the relax-and-fix strategy, a time limit of 1 h was used. (The influence of this time limit on the comparison will be analyzed later in this section.) Furthermore, in the relax-and-fix strategy, the time was divided linearly between the subproblems such that the first subproblem has twice as much time as the last. Preliminary tests when supplying three times as much time to the first subproblem and dividing the time evenly among the subproblems showed similar results. The last column of the table shows that, in aggregate, that is, without evaluating the different values of K and the groups of instances individually, all strategies improved upon the results obtained with CPLEX, with gap values ranging from $-22\%$ to $-37\%$. The numbers also show that strategy S1 provided the best results. It is also worth noting that S1 found feasible solutions for all instances and all tested values of K.

Table 4 shows the disaggregated results for strategy S1: that is, for each value of K separately. Figure 3 graphically shows the same results shown in Table 4. The numbers in the table show that, except for the case $K=2$, the results vary little depending on the value of K chosen, which can be considered as a positive feature of the method. The numbers also show that the relax-and-fix strategies with $K \ge 3$ almost always surpass CPLEX, except for some instances of groups A and B that concentrate the smallest instances.

Table 3 General performance of hybrid strategies S1 to S9 with S11 as a tie-breaking rule plus standalone strategies S10 and S11 on random instances

Table 4 Detailed performance of strategy S1 with S11 as a tie-breaking rule varying $K \in \{2, 3, \dots , 10\}$ on random instances

Fig. 3

Gaps to CPLEX solution (i.e., $K=1$) of strategy S1 on random benchmark instances

The comparison with CPLEX depends very much on the 1-h time limit being used, since if the instance is small and CPLEX is able to find an optimal solution (regardless of whether it can prove whether the solution is optimal or not), then there is nothing that relax-and-fix can do. Therefore, we decided to test the influence of the time limit on the comparison. To this end, we reran CPLEX and strategy S1 with time limits of 600, 1, 200, 1, 800, 2, 400, 3, 000 and 3, 600 s. We considered S1 with $K=6$ because Table 4 shows that this was the best value of K for such a strategy. However, this does not mean that we intend to use these values of K in the next experiments, since as already mentioned before, the method is robust and shows small variations with respect to the value of K. Figure 4 shows the results for strategy S1 (with $K=6$). Figure 4a shows that when the time limit is reduced, the advantage of the relax-and-fix strategy increases. The average gap versus CPLEX, which was $-40.62\%$ for the 1-h time limit, extended to $-65.79\%$. This experiment shows that with less time available, using the relax-and-fix strategy is even more advantageous. However, the question that remains is as follows: With less time, how much do the solutions found by relax-and-fix deteriorate? Fig. 4b compares the solution obtained by relax-and-fix with a reduced budget against the solution found with the 1-h budget. The figures show that the maximum deterioration is, on average, approximately $24.23\%$. The deterioration of the solutions found by CPLEX with reduced time is much greater, which is why the advantage of the relax-and-fix strategy increases.

Fig. 4

a Boxplot of the gaps between CPLEX and strategy S1 ($K=6$) applied to the 50 random instances varying the time limits of the methods. (The average gaps are $-65.79\%$, $-52.86\%$,$-45.62\%$, $-43.14\%$, $-39.75\%$, $-40.62\%$ for the time limits $600, 1{,}200, \dots 3{,}600$, respectively). b Boxplot of the gaps between S1 ($K=6$) applied to the 50 random instances varying its time limit in $\{600, 1{,}200, \dots , 3{,}000\}$ and S1 ($K=6$) with a 1-h time limit. (The average gaps are $24.23\%$, $12.73\%$, $6.82\%$, $4.84\%$, $1.57\%$ for the time limits $600, 1{,}200, \dots 3{,}000$, respectively)

5.2 Experiments with Real-world Instances

In this section, we apply the presented methods to eight real instances provided by the company. All instances, as well as the randomly generated ones, include 16 periods divided into 7 subperiods. The number of machines varies between 2 and 7, and the number of products varies between 8 and 26. Table 5 shows some details of the instances and their respective models. Recall that in the table, IV, CV and CO stand for “integer variables”, “continuous variables”, and “constraints”. The table also shows, for each instance, the solution found by the company, which was calculated by an expert with an undisclosed empirical method.

Table 5 Detailed information of the real-world instances

The results with the random instances showed that there is no clear advantage of a certain value of K over others (excluding small values of K) and that small variations in the values of K generate small variations in the results. Because of this and because we do not know how the solutions given by the company were calculated, we solved the eight instances with strategy S1 while varying the time limit and varying K, as we did with the random instances. Figure 5 shows the results. On the one hand, the figure shows that, for fixed K, the longer the time limit, the better the solution found. On the other hand, the figure also shows that strategy S1 finds very similar values for any $K \ge 6$. Because of this, we arbitrarily fixed $K=8$.

Table 6 shows the results obtained by strategy S1, with $K=8$ and varying time limit. The table also shows the results obtained by CPLEX while also varying the time limit. For each method and time limit, the table shows the solution obtained and the gap in relation to the solution presented by the company, calculated as

$$\begin{aligned} 100 \times \left( ( F_{\textrm{method}} - F_{\textrm{company}} ) / F_{\textrm{company}} \right) \%, \end{aligned}$$

where $F_{\textrm{method}}$ and $F_{\textrm{company}}$ correspond to the objective function values of the solutions found by the method and the company, respectively. The numbers in the table show that the proposed strategy always improves the company’s solution by an amount that roughly varies, on average, between 40% and 46%, depending on the time limit given for the strategy. The solutions found by CPLEX are, on average, worse than the solutions reported by the company when the timeout is 600 or 1,200 s, while CPLEX improves the company’s solutions on average between 24% and 35% for longer time limits.

Fig. 5

Average gap to the company’s solution of solutions found by strategy S1 varying $K \in \{2, 3, \dots , 10 \}$ and the CPU time limit in $\{600, 1{,}200, \dots , 3{,}600\}$ s

Table 6 Gap between solutions found by CPLEX and strategy S1 (with $K=8$) and the company’s solutions, with varying CPU time limits in $\{600, 1{,}200, 1{,}800, 2{,}400, 3{,}000, 3{,}600\}$

Figure 6 shows the data from Table 6 in a different way. In the figure, for each instance, the solution reported by the company corresponds to 100% and the solutions found by the other methods (CPLEX and strategy S1) appear as percentages of the solution reported by the company. In the figure, CPLEX appears in light blue, while strategy S1 appears in violet. Additionally, for each method and each instance, there are 6 thin bars that, from left to right, correspond to the time limits $600, 1{,}200, \dots , 3{,}600$. Bars that exceed 100% appear truncated in the figure for presentation purposes, and their true values are indicated with numbers near the top. Note, for example, that in instances P1 and P3, the 6 thin bars of each method have practically the same height. This means that these instances are apparently simple for the methods, which practically find the same solutions regardless of the time limit. For the other instances, the 6 thin bars associated with different time limits seem to have decreasing height from left to right, which shows that, with more time, the methods are able to find better solutions.

Overall, as already determined by examining Table 6, both CPLEX and strategy S1 improve the solutions reported by the company, except for instances P6 and P8, where CPLEX found worse solutions for threshold times below 1,800 s. Regardless, the performances of CPLEX and strategy S1 are similar in instances P1, P2, P3 and P4. In these 4 instances, the methods improve the solution presented by the company and return very similar solutions. It is worth noting that these 4 instances are the smallest instances, with dimensions similar to the random instances of groups A and B. In these instances, using CPLEX would be a reasonable alternative. The situation is different in instances P5, P6, P7 and P8, which are the largest within the set considered. In these instances, strategy S1 substantially improves the solutions found by the company in a way that is not matched by CPLEX. Note that even in instances P5, P6 and P8, the solutions found by strategy S1 with the shortest time limit are better than the solutions found by CPLEX with the longest time limit considered.

Fig. 6

Solutions obtained with CPLEX and strategy S1 (with $S=8$) as a percentage of the company’s solutions

5.3 Sensitivity Analysis with Respect to Storage Capacity Constraints

In this section, we perform a basic sensitivity analysis with respect to the storage capacity constraint of the warehouse. This analysis is in fact pertinent because, in the problem considered, storage capacities can be modified rather quickly and at low cost. Leasing or unleasing a warehouse can be done in a few weeks, while, for example, buying and installing a new production machine can take 3 to 5 years. Moreover, the storage capacities considered in real-world instances are intentionally large. On the one hand, the cost of inventory comprises the cost of having resources invested in a commodity stalled in inventory, the cost of the physical space itself, and the cost of handling the inventory. Because many of the items produced are of little value, these three components contribute approximately 20%, 40% and 40% to the cost of inventory, respectively. On the other hand, the backordering cost is relatively high in relation to the inventory cost. Because of this, the solution currently adopted by the company is to produce in advance and store stock to minimize the chance of failing to meet the demand.

To carry out the analysis, we considered, as an example, the real-world instance P6. (The scenario is very similar in the other real-world instances.) Solutions were computed with strategy S1 with $K=8$ and a CPU time limit of 2 h. For the solution found for this instance, the warehouse capacity constraint is inactive for every instant $t \in \mathcal {T}$; and $\max _{i \in \mathcal {I}, \; t \in \mathcal {T}} \{I_{it}^+\} = 457{,}395$. Therefore, we redefined $C^W = 457{,}395 - 1$ and solved the instance again. This procedure was repeated until the instance became infeasible. In the particular case of instance P6, the last solved feasible problem had $C^W = 452{,}939$ and $\max _{i \in \mathcal {I}, \; t \in \mathcal {T}} \{I_{it}^+\} = 452{,}834$, and the instance is infeasible if we consider $C^W = 452{,}833$. Figure 7 shows the objective function value of the solutions obtained as a function of the considered value for $C^W$. The first observation is that the warehouse capacity can be reduced from its original value of 650, 000 to 457, 395 without any impact on the quality of the solution obtained. On the other hand, Fig. 7 shows that reducing $C^W$ from 457, 395 to 452, 834 produces an increase in the objective function value from 451, 067.20 to 494, 141.00. Evidently, this reduction in storage capacity would only be justified if it brought savings of more than 43, 073.80.

Additionally, it should be noted that this analysis does not consider the potentially negative impact of the reduction of warehouse capacity on the inventory cost of products. It would be reasonable to assume that there is a gain of scale when considering large warehouses and that a reduction in the warehouse capacity can increase the 40% share of the physical space that goes into the inventory cost of each product. A deeper parametric analysis, which takes this relationship into consideration, could be performed if the company would effectively be willing to adopt the production scheduling suggested in this study instead of the current policy of production in advance. Furthermore, the analysis could provide a basis for the discussion of contractual backordering costs in the sense that smaller warehouses could be used if the costs for late deliveries were lower or within a certain range.

Fig. 7

Objective function value at the solution found as a function of the capacity of warehousing $C^W$ in the real-world instance P6

6 Conclusions

This paper addressed an integrated real-world lot sizing and scheduling problem in a complex operating environment that occurs in a large company in the personal care consumer goods industry. This problem is composed of distinct parallel machines with limited production capacity and sequence-dependent setup times and costs. There is also limited storage capacity for finished goods. To solve this problem, a MILP model was presented, and several problem-dependent and problem-independent strategies based on the relax-and-fix heuristic were developed. The performance of the heuristics was evaluated by solving randomly generated instances and real-world cases. Exhaustive details about the parameters of the real instances are given (see Table 1) in such a way that new random instances can be generated that preserve the characteristics of the real instances. This allows the generation of new test sets to evaluate and compare methods that apply to the problem under consideration.

The relax-and-fix strategies introduced showed the best results overall. Strategy S1, which prioritizes chronological time, showed robustly superior performance compared to the other strategies. In addition, the performance of the relax-and-fix strategies was compared with actual results achieved by the company and the results obtained by solving the MILP model using CPLEX. Compared to the actual solutions used by the company, the strategies produced results with lower costs and a cost reduction between 40% and 46%, mainly from the reduction of inventory levels and better allocation of production lots on the machines. The relax-and-fix heuristics also outperformed CPLEX applied to the MILP model. The proposed strategy confers the advantages of being applicable with minimal technical knowledge and relying on well-established software that solves subproblems. This offers the company confidence in its decision-making. Due to the successful application of the proposed methods, the ideas presented in this work are now being extended to more complex production and logistics environments with multiple distribution centers and factories that are also operated by the target company.