1 Introduction

\(\hbox {CO}_{2}\) emissions in the European transport sector are regulated by limiting car manufacturer’s fleet emissions. As the EU Commission’s targeted emission limit of 95 g \(\hbox {CO}_{2}\)/km for 2020 can no longer be reached by an exclusive use of conventional power train technologies [1], research efforts in the industry increasingly shift toward the development of alternative power train technologies. Electric traction drives commonly serve as the basis for these. Due to their material properties, the utilization of polymers in electrical applications is very widespread. Examples of polymer use in electric machines range from primary winding or rotor stack isolation to component adhesion, but may also include usage as a matrix material in electromagnets.

Foundation for the strength evaluation of such materials using finite element analysis is the material model. However, data typically made available in technical data sheets does not allow for an adequate model identification and parametrization. Mechanical stiffness properties at ambient temperature, for example, cannot simply be extrapolated to identify the stiffness at higher or lower temperatures, and the influence of rate dependence on any given value is unknown. Additionally, published mechanical properties primarily provide short-term material properties, but rarely take into consideration a polymer’s pronounced long-term relaxation behavior or aging.

Epoxy is a thermoset polymer which typically exhibits viscoelastic behavior. The constitutive equation for linear, non-isothermal viscoelastic solids was originally formulated by Christensen und Naghdi [2], and generally serves as the foundation for more refined material modeling approaches [3]. Linear viscoelasticity is valid under the condition of the Boltzmann superposition principle and thermorheological simplicity. A material behaves thermorheologically simple if all characteristic functions, such as creep or relaxation modulus, exhibit the same time-temperature shifting pattern.

A mathematical relationship between time and temperature to account for the influence of temperature on a material’s relaxation behavior within the framework of linear viscoelasticity can be established through definition of a shift factor. The most common shift factors are given through the Arrhenius equation [4] or WLF equation by Williams-Landel-Ferry [5]. Choice of the most applicable model is dependent on material state and application, among others. The validity of the time-temperature superposition principle can be explained in theory through molecular-based structural models [6]. For further information on linear viscoelasticity, however, the reader is referred to more comprehensive reference works [7, 8].

An influence of additional phenomena for a more accurate description of the relaxation behavior can be accounted for by modification of the time-temperature relation’s shift factor [3, 9,10,11,12,13,14,15,16,17,18,19,20]. This topic is covered extensively in Hutchinson [9] and Roth [3], which serve as the basis for the following summary. Within the scope of isotropic viscoelasticity, a material’s free volume can exemplary be factored in through approaches by Vogel-Fulcher-Tammann [10,11,12] or Doolittle [13]. The influence of free volume on structural relaxation goes back to a hypothesis by Cohen [21] and Turnbull [22] stating that a certain molecular mobility given by a critical volume per mole is responsible for the rate of molecular rearrangement [3]. Many works, such as those by Knauss [14] and Losi [15], build on this approach either by refinement or experimental validation. The influence of volume or enthalpy regarding material relaxation is alternatively considered in the tnm model [23,24,25] under condition of a continuous distribution of relaxation times as formulated by Kohlrausch [16], Williams and Watts [17]. Known as the kahr model, a model by Kowasz, Aklonis, Hutchinson and Ramos [18] alternatively describes this relaxation by use of a discrete distribution of relaxation times. Finally, the influence of entropy on relaxation is considered in models by DiMarzio and Gibbs [19] or Adam and Gibbs [20].

Even though the aforementioned models are motivated and guided by the physics behind molecular kinetics, they are essentially phenomenological in nature. As an alternative, the influence on material relaxation can be described using a fundamental modeling approach that further describes the molecular relaxation processes. Within the framework of isotropic viscoelasticity, models for example attempt to explain polymer relaxation by describing it as a result of molecular rearrangement in regions of especially high free volume that stem from thermal fluctuations with a strong local restriction to the nanometer scale [26]. Approaches like this allow for further considerations of molecular motion-inspired dependencies, as exemplified here through the consideration of a dependence to the structural composition. An impact of continuum variables such as stress or strain on the deformation behavior can be considered as well, by use of nonlinear viscoelastic stress-dependent [27,28,29,30] and strain-dependent [27, 31, 32] material models. Horstemeyer gives a comprehensive historical overview of many such model adjustments [33].

Aim of this work is the identification, implementation, parametrization, and validation of an appropriate material model of a filled epoxy system which is to be evaluated for the use as a potting material in active rotor components of electric traction drives. Goal of the material model is to enable structural finite element analyses within a temperature range of \({20}^{\circ }\hbox {C}\) and \({180}^{\circ }\hbox {C}\) in order to quantify thermo-mechanical loads during motor assembly and operation.

Table 1 Experimental program–characterization of a filled epoxy system
Full size table

2 Characterization of material behavior

2.1 Experimental program

An overview of the material tests which make up the experimental program is provided in Table 1. It is made up of multiple sequential steps. Initially, the material composition and curing conversion is identified to ensure correct material composition and curing completion of all test specimens. Next, the assessment of material classification allows for an identification of relevant material phenomena, which are to be characterized further. Based on this classification, an appropriate material model can be derived as well. Finally, in order to fully parametrize and validate this model, material testing of the deformation and failure behavior follows.

2.2 Experimental setup and test specimen preparation

All initial tensile and step relaxation tests with intermediate unloading were carried out using a mechanical wedge-clam** unit in favor of the more common hydraulic clam** unit, to ensure consistent use even at elevated temperatures (\({180}\,^{\circ }\hbox {C}\)). Due to the fact, that traction between the mechanical wedge-clam** unit and the test specimen at low loads cannot be guaranteed, minimum load limits for the unloading process in between relaxation phases were set to 1,25 MPa. Strain measurements were carried out using a video extensometer with an effective measurement length of \(l_{\text {m}}= {60}\,\hbox {mm}\).

The tensile test specimens of Type 1B, as defined in ISO 527-2, were cut into final form by use of high-pressure water jetting. All standardized test specimens were vacuum-cast into plates and then cured. It must be noted that due to the prototype nature of the evaluated material, compression tests were carried out using a resin sample with a slightly altered filler composition. The test results are presented nonetheless, because filler amount, glass transition temperature, tensile strength, the coefficient of thermal expansion as well as the heat conductivity show no significant deviation. All tensile tests at ambient temperature were carried out in a climate-controlled laboratory environment. Experiments at elevated temperatures (i.e., \({100}^{\circ }\hbox {C}\) and \({180}^{\circ }\hbox {C}\)) were carried out in a convective heat chamber, which was positioned around the clam** unit. All test specimens were normalized for at least 16 h prior to use.

2.3 Experimental procedure

The testing program setup parameters are summarized in Table 2. For the initial material characterization,

Table 2 Testing parameters–experimental setup
Full size table

A dynamic mechanical analysis (DMA) is performed. Next, displacement-controlled tensile tests at ambient and elevated temperatures are run until failure. Differences in the stress-strain curves at various strain rates allow for a conclusion regarding material rate dependence. The tests also allow for conclusions regarding the qualitative characterization of temperature dependence.

A mechanical deformation characterization is then carried out by means of step relaxation tests with intermediate unloading, and holding times of \(t_h={10}\,\hbox {min}\) at each strain level \(\varepsilon _{1\dots 4}\). The utilized displacement rates \(\dot{u}_1\), \(\dot{u}_2\), and \(\dot{u}_3\) are graded in decades around \(\dot{u}= {5}\,\hbox {mm/min}\), which is the recommended displacement rate for brittle materials with an elongation at break of \(\varepsilon _{\text {zB}}\,\le \,{10}{\%}\) [34]. The increment between each strain level is defined as \(\Delta {\varepsilon } = {0,1}{\%}\). After four performed pull-hold-relaxation cycles, the test is completed by a monotonic tensile test to failure. Due to lag in the control feedback loop between the universal testing machine and its video extensometer strain measurement system, the target strain may be exceeded by up to 0,5%, depending on temperature and displacement rate. This is indicated in Sect. 2.4, where the strain increments as shown in the step relaxation test with intermediate unloading at ambient temperature (Fig. 3a) measure \(\Delta {\varepsilon }^{{23}^{\circ }\hbox {C}} = {0,1}{\%}\), and at elevated temperature (Fig. 3b) \(\Delta {\varepsilon }^{{180}\,^{\circ }\hbox {C}}= {0,25}{\%}\). This effect however is not relevant for the following material model parametrization.

After performing a thermomechanical analysis (TMA), effective curing is characterized by measuring the deflection of a specialized two-component test specimen. The potting material is applied and cured on an aluminum substrate. Superimposed contraction of chemical shrinkage during conversion and thermal shrinkage from the subsequent cool down to ambient temperature results in a measurable test specimen deflection. With the thermomechanical material properties of both components known, the effective deformation can be separated into a chemical and a thermal component, allowing a quantification of the effective curing shrinkage.

2.4 Experimental results

2.4.1 Initial characterization results

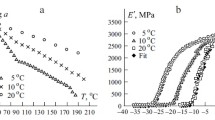
The DMA loss modulus peak (Fig. 1b) clearly indicates an average glass transition temperature \(T_{\text {g}}\) of \({181,26}^{\circ }\hbox {C}\). The material phase state is therefore glassy for all relevant temperatures.

Fig. 1
figure 1

Initial characterization–dynamic mechanical analysis

Full size image

2.4.2 Classification of material behavior

The monotonic tensile tests (Fig. 2) enable a first indication of the material behavior. Strain rate and temperature dependencies are both apparent.

Fig. 2
figure 2

Tensile tests at ambient temperature (\(T_1\), \(\dot{\varepsilon }_{1\dots 3}\)) and elevated temperature (\(T_3\), \(\dot{\varepsilon }_{1\dots 3}\))

Full size image

Higher strain rates result in a higher effective stiffness, while higher temperatures in contrast result in a lower effective stiffness. The material dependence on temperature is more pronounced than its strain rate dependence. Compared to thermoplastic materials such as polypropylene [35], the strain rate dependence of the herein evaluated thermoset in its glassy state is comparatively low. Yet, the material clearly shows viscous traits in its behavior. This observation is further supported by the results of the step relaxation tests with intermediate loading (Fig. 3).

Fig. 3
figure 3

Step relaxation tests with intermediate unloading at a ambient and b elevated temperature

Full size image

The stress-time curves show clear signs of relaxation over the duration of the strain holding time \(t_{\text {h}}= {10}\,{min}\) at all strain levels \(\varepsilon _{1\dots 4}\).

2.4.3 Deformation characterization results

The video extensometer greyscale correlation analysis shows temperature-dependent Poisson’s ratios of \(\nu (T_0)=0.12\), \(\nu (T_1)=0.19\), and \(\nu (T_3)=0.29\) (see Table 2). Generally, a polymer’s Poisson ratio approaches \(\nu = 0.5\) when nearing its rubbery state at highly elevated temperatures [36]. However, a convergence of the measured Poisson’s ratio during its glass transition toward \(\nu ^{{180}^{\circ }\hbox {C}} = 0.5\) is not observed, albeit its proximity to its glass transition temperature of \(T_{\text {g}} = {181,26}^{\circ }\hbox {C}\). This is concluded to be a result of the potting material’s high filler content and marks an important differentiating feature of highly filled epoxy systems.

Figure 4 depicts the experimental results of the TMA.

Fig. 4
figure 4

Thermomechanical analysis

Full size image

As expected, the coefficient of thermal expansion is highly temperature dependent, with values as high as \({50 \times 10^{-6}}{K^{-1}}\) when approaching the glass transition temperature. Any further reduction in the measurements to a single coefficient of thermal expansion for temperatures above and below glass transition is likely to introduce significant errors.

The mean test specimen deflection as characterized during the curing shrinkage analysis is 0,56 mm. As this deflection is measured at ambient temperature, the bending of the test specimen is a result of a superimposed contraction due to chemical shrinkage from curing, as well as the thermal contraction from the subsequent temperature drop. The influence of thermal contraction is primarily dependent on the thermal expansion coefficient and the gelation temperature, while the influence of chemical contraction mainly depends on the epoxy system, filler amount and filler type.

2.4.4 Strength characterization results

The tensile strength at ambient temperature is \(\sigma ^{{23}^{\circ }\hbox {C}}_{\text {zB}} = {78,4}\,\hbox {MPa}\) with an elongation at break of \(\varepsilon _{\text {zB}}^{{23}^{\circ }\hbox {C}}= {0,56}{\%}\). The standard deviation is 1,1 MPa and 0,01%, respectively. At elevated temperature \(T_3\), a tensile strength of \(\sigma _{\text {zB}}^{{180}^{\circ }\hbox {C}}={29,1}\, \hbox {MPa}\) with an elongation at break of \(\varepsilon _{\text {zB}}^{{180}^{\circ }\hbox {C}} = {1,02}{\%}\) is measured. Here, the standard deviation is 1,8 MPa and 0,13%, respectively.

In compression at ambient temperature \(T_1\), a compressive strength of \(\sigma ^{{23}^{\circ }\hbox {C}}_{\text {dB}} = {223,0}\,\hbox {MPa}\) of the 5 perpendicular prism test specimen at a standard deviation of 8,7 MPa, at elevated temperature \(T_3\) of \(\sigma _{\text {dB}}^{{180}^{\circ }\hbox {C}} = {88,9}\hbox {MPa}\) at a standard deviation of 4,3 MPa is measured.

The discrepancy between tensile and compressive strength values is a known phenomenon of polymeric materials [37,38,39]. It can be traced back to a dependence on the deformation mechanisms and the material’s molecular structure to its hydrostatic stress state [40]. Under tensile load, the molecular chains align in a nematic bond order. In addition, tensile loads result in a higher degree of strength-impacting polymer unfolding [41]. Nonetheless, the compressive-to-tensile strength ratio of \(m^{{23}^{\circ }\hbox {C}}_{\text {dz}}={2,85}\) at ambient temperature and \(m^{{180}^{\circ }\hbox {C}}_{\text {dz}}= {3,05}\) at elevated temperature is comparatively high. Common strength ratios in academic literature as used for the determination of appropriate failure criteria are in the range of \(m_{\text {dz}}= 1.2\dots 1.3\) for unfilled thermoplastic materials in general, and \(m_{\text {dz}}= 1.45\) for unfilled epoxy resins [40, 42,43,44]. The ratios of silica or alumina filled casting resins are on average \(m_{\text {dz}}= 2.5\), and glass fiber-reinforced or mineral filled bisphenol molding on average \(m_{\text {dz}}= 2.4\) [45].

3 Modeling of material behavior

Precondition for the applicability of a linear viscoelastic material model is the Boltzmann principle of stress-strain linearity. The time-corrected stress-strain curves may be evaluated according to the following principle as summarized by Starkova [46], which is based on the works by Reiner [47] und Brüller [48]. It allows the identification of limits to a material’s linear viscoelasticity by utilization of the rate independent tensile stress \(\overline{\sigma }\)

$$\begin{aligned} \overline{\sigma }=ln\Big (\sigma (t)/\dot{\varepsilon }\Big )\;, \end{aligned}$$
(1)

the stress-strain curves of the monotonic tensile tests (Fig. 2) are translated into the \(ln(\sigma (t)/\dot{\varepsilon })\)-ln(t) space and evaluated for linearity. Only if the curves do not deviate significantly from a straight line, the material behavior may be assumed linear. An exemplary assessment for the strain rate \(\dot{\varepsilon }_1\) is given in Fig. 5.

Fig. 5
figure 5

Assessment of stress-strain linearity rate-independent stresses \(\overline{\sigma }_{\text {z}}^{{23}^{\circ }\hbox {C}}\) and \(\overline{\sigma }_{\text {z}}^{{180}^{\circ }\hbox {C}}\) from monotonic tensile tests (\(T_{1,3}\), \(\dot{\varepsilon }_1\))

Full size image

Due to the fact, that the material response, and thus potential nonlinearities, may be dependent on a multitude of external factor, e.g., temperature, stress, strain, strain rate, the scope of this assessment is limited to the parameters listed in Table 2.

3.1 Model for linear viscoelastic material behavior

3.1.1 Uniaxial model

Using the analogy of a rheological model made up of springs and dampers, material relaxation spanning multiple decades within the framework of linear viscoelasticity can be described by the generalized Maxwell model consisting of N Maxwell bodies in parallel and one Hooke element. The resulting relaxation behavior \(E_{\text {R}}(t)\) is mathematically represented by a Prony function

$$E_{{\text{R}}} (t) = E_{\infty } + \sum\limits_{{i = 1}}^{N} {E_{{{\text{R}},i}} } \left( {e^{{ - \frac{t}{{\tau _{{{\text{R}},{\text{i}}}} }}}} } \right)$$
(2)

as the summation of all weighted exponential functions. The relaxation spectrum \(\{\tau _{\text {R},i}, E_{\text {R},i}\}\) for each element i of the N Maxwell elements is defined as the ratio of viscosity \(\eta _i\) and stiffness \(E_{\text {R},i}\)

$$\begin{aligned} \tau _{\text {R},i}=\frac{\eta _{i}}{E_{\text {R},i}} \;. \end{aligned}$$
(3)

The smallest required relaxation time \(\tau _{\text {R,min}}\) of 0,1 s is derived from the time measurement signal resolution \(\Delta t_\text {m}={0,01}\,\hbox {s}\) [49]. The longest required relaxation time \(\tau _{\text {R,max}}\) depends on the total time frame of the relaxation master curve and is defined later. In order to ensure continuous control over the relaxation behavior, one relaxation time constant \(\tau _{\text {R}}\) is required for each decade of time [50]. The relaxation time spectrum is therefore defined as

$$\begin{aligned} \{\tau _\text {R}\}=\Big [10^{-1}\;\;10^0\;\;10^1\;\;10^2\;\;\dots \Big ]^{T}\hbox {s} \;. \end{aligned}$$
(4)

3.1.2 Generalization to multiaxial and thermo-chemo-mechanical loadings

The generalization toward multiaxial stress and strain states can be accomplished by a decomposition of the stiffness \(E_{\text {R}}\) into bulk and shear stiffness K and G by use of Poisson’s ratio \(\nu\). This dimensionless characteristic value describes the transversal contraction of the material and can be rate and temperature dependent [36, 51,52,53,54]. For a viscoelastic isotropic material, a correlation between the values is given by

$$\begin{aligned} \nu (t)=\frac{3K(t)-2G(t)}{6K(t)+2G(t)} \;. \end{aligned}$$
(5)

In terms of the Prony series (2), the deviatoric relaxation behavior is written as

$$\begin{aligned} G(t)=\frac{E_{\text {R}}(t)}{2\big (1+\nu (t)\big )},\;\;\; K(t)=\frac{E_{\text {R}}(t)}{3\big (1-2\nu (t)\big )} \;. \end{aligned}$$
(6)

Taking into account that

$$\begin{aligned} G_{\infty }=G_0\Bigg (1-\sum _{i=1}^Ng_i\Bigg ),\;\;\; K_{\infty }=K_0\Bigg (1-\sum _{i=1}^Nk_i\Bigg ) \;, \end{aligned}$$
(7)

with \(g_i=G_i/G_0\) and \(k_i=K_i/K_0\) representing the dimensionless shear and bulk modulus, and \(G_0\) and \(K_0\) representing the instantaneous shear and bulk modulus, respectively, the shear relaxation behavior is

$$\begin{aligned} G(t)=G_0\left( 1-\sum _{i=1}^{N}g_{i}\left( 1-e^{-\frac{t}{\tau _{\text {R},i}}}\right) \right) \;, \end{aligned}$$
(8)

and the bulk relaxation behavior K is

$$\begin{aligned} K(t)=K_0\left( 1-\sum _{i=1}^{N}k_{i}\left( 1-e^{-\frac{t}{\tau _{\text {R},i}}}\right) \right) \;. \end{aligned}$$
(9)

The constitutive law governing linear isotropic viscoelasticity in the three-dimensional stress state \(\varvec{\sigma }\) is given by [55]

$$\begin{aligned} \varvec{\sigma }(t)&=\int _{0}^{t} 3K(t-\tau ) \frac{d}{d\tau }\varvec{\varepsilon }^{\text {H}}\left( \tau \right) d\tau \nonumber \\&\quad + \int _{0}^{t} 2 G\left( t-\tau \right) \frac{d}{d\tau }\varvec{\varepsilon ^{\text {D}}}(\tau ) d\tau \;. \end{aligned}$$
(10)

\(\varvec{\varepsilon }\) is the infinitesimal strain tensor.

The first integral in Eqs. (18) is the hydrostatic stress

$$\begin{aligned} \varvec{\sigma ^\text {H}}(t)= \int _{0}^{t} 3K(t-\tau ) \frac{d}{d\tau }\varvec{\varepsilon }^{\text {H}}\left( \tau \right) d\tau \;. \end{aligned}$$
(11)

With no shear stresses in either of the three planes, \(\varvec{\sigma ^\text {H}}\) describes the stress state responsible for volumetric changes with no change in shape. Here, the corresponding hydrostatic strain rate \(\varvec{\dot{\varepsilon }^\text {H}}\) is given by

$$\begin{aligned} \frac{d}{dt}\varepsilon ^{\text {H}}_{ij}\left( t\right) = \sum _k\frac{1}{3}\dot{\varepsilon }_{kk}\delta _{ij} \;, \end{aligned}$$
(12)

and the Kronecker delta \(\delta _{ij}\) is defined as

$$\begin{aligned} \begin{matrix} \delta _{ij} = \Bigg \{ \end{matrix} \begin{matrix} \;1, &{} \text {if} &{} i=j\;, \\ \;0, &{} \text {if} &{} i\ne j\;. \end{matrix} \end{aligned}$$
(13)

The second integral in Eqs. (18) is the stress component deviating from the hydrostatic stress state in Eqs. (11)

$$\begin{aligned} \varvec{\sigma ^\text {D}}(t)=\int _{0}^{t} 2 G\left( t-\tau \right) \frac{d}{d\tau }\varvec{\varepsilon ^{\text {D}}}(\tau ) d\tau \;. \end{aligned}$$
(14)

It is termed deviator and describing the stress state responsible for shape changes with no changes in volume. In it, the deviatoric strain rate \(\varvec{\dot{\varepsilon }^\text {D}}\) is given by

$$\begin{aligned} \frac{d}{dt}\varepsilon _{ij}^{\text {D}}(t)=\dot{\varepsilon }_{ij}-\sum _k\frac{1}{3}\dot{\varepsilon }_{kk} \delta _{ij} \;. \end{aligned}$$
(15)

The effect of temperature changes is taken into account in terms of purely volumetric thermal strains [3]

$$\begin{aligned} \varvec{\varepsilon }^{\text {T}}(t)=\varvec{\varepsilon }^{\text {T,H}}(t)=\frac{1}{3}\int _0^t\alpha (t-\tau )\varvec{I}\frac{d}{d\tau }T(\tau )d\tau \;. \end{aligned}$$
(16)

\(\alpha\) is the coefficient of thermal expansion, T denotes the temperature. The total strain

$$\begin{aligned} \varvec{\varepsilon }(t)=\varvec{\varepsilon }^{\text {el}}(t)+\varvec{\varepsilon }^{\text {T}}(t)=\varvec{\varepsilon }^{\text {el,H}}(t)+\varvec{\varepsilon }^{\text {T,H}}(t)+\varvec{\varepsilon }^{\text {D}}(t) \; \end{aligned}$$
(17)

is additively decomposed into elastic and thermal volumetric and purely elastic deviatoric contributions.

According to the extended constitutive law governing linear isotropic thermo-viscoelasticity stresses result only from elastic strain components

$$\begin{aligned} \varvec{\sigma }(t)&=\int _{0}^{t} 3K(t-\tau ) \frac{d}{d\tau }\varvec{\varepsilon }^{\text {el,H}}\left( \tau \right) d\tau \nonumber \\&\quad + \int _{0}^{t} 2 G\left( t-\tau \right) \frac{d}{d\tau }\varvec{\varepsilon ^{\text {D}}}(\tau ) d\tau \;. \end{aligned}$$
(18)

Chemical shrinkage during curing may be modeled as an isotropic contraction. The curing process itself is non-isothermal and usually occurs within a temperature delta \(\Delta T\) spanning from gelation temperature \(T_{\text {gel}}\) to ambient temperature \(T_1\). The resulting change in volume thus consists of superimposed thermal and chemical expansion and can be expressed by a modified expansion coefficient \(\alpha '\)

$$\begin{aligned} \alpha '=\alpha +\alpha ^{\text {C}} \;, \end{aligned}$$
(19)

where \(\alpha ^\text {C}\) signifies the chemical expansion coefficient. Analogously to the pure thermal strains \(\varepsilon ^\text {T}\) in Eqs. (16), the superposition of thermal and chemical strains \(\varepsilon ^\text {T,C}\) during curing is expressed as

$$\begin{aligned} \varvec{\varepsilon }^{\text {T,C}}(t)=\frac{1}{3}\int _0^t\alpha '(t-\tau )\varvec{I}\frac{d}{d\tau }T(\tau )d\tau \;. \end{aligned}$$
(20)

3.1.3 Time-temperature superposition

The effect of temperature on the material behavior is modeled in terms of the time-temperature superposition principle [56], which provides a mathematical relationship between relaxation curves at different temperatures \(E_{\text {R}}(\xi ,T)\) and \(E_{\text {R}}(t,T_{\text {ref}})\)

$$\begin{aligned} E_{\text {R}}(\xi ,\text {T})=E_{\text {R}}(t,T_{\text {ref}}) \;. \end{aligned}$$
(21)

Necessary precondition is thermorheological simplicity. Modification of the intrinsic material time, i.e., a time adjustment from t to \(\xi\), of the known relaxation response at reference temperature \(T_{\text {ref}}\) thus allows the prediction of the relaxation response \(E_{\text {R}}\) at another temperature T. The effective time \(\xi\)

$$\begin{aligned} \xi =\int _0^t\frac{d\tau }{a_{\text {T}}\left( T\left( \tau \right) \right) } \end{aligned}$$
(22)

is used to identify the shift function \(a_{\text {T}}\) describing the correlation between actual time t and effective time \(\xi\). The master relaxation curve \(E_{\text {R}}(t,T_{\text {ref}})\) at the given reference temperature is shifted horizontally on the logarithmic time scale by the amount \(a_{\text {T}}\), allowing the description of the relaxation behavior \(E_{\text {R}}(\xi ,T)\) at other temperatures.

As the previously characterized filled potting material’s glass transition temperature of \(T_{\text {g}}= {181,26}^{\circ }\hbox {C}\) (Fig. 1c) is above the temperature range of interest, time-temperature superposition is governed by the Arrhenius function. It applies to polymers in their glassy state [3].

$$\begin{aligned} \text {log}_{10}(a_{\text {T}})=-\frac{E_{\text {a}}}{2,303R}\left( \frac{1}{T-T_{\text {zero}}}-\frac{1}{T_{\text {ref}}-T_{\text {zero}}}\right) \;, \end{aligned}$$
(23)

with the activation energy \(E_{\text {a}}\), the universal gas constant \(R= {8,314}\,\hbox {J/mol K}\), and the absolute zero \(T_{\text {zero}} = {-273,15}^{\circ }\hbox {C}\).

3.2 Material model parametrization

3.2.1 Identification of the shift function

The parametrization of time and temperature-dependent material behavior within the framework of linear thermo-viscoelasticity firstly requires the quantification of the relationship between time and temperature. With time-temperature superposition chosen to be governed by the Arrhenius equation, the characteristic value describing this relationship is the activation energy \(E_{\text {a}}\). The identification is carried out using stress curves of the step relaxation tests with intermediate unloading of all three testing temperatures \(T_{1\dots 3}\) at a maximum strain rate of \(\dot{\varepsilon }_{\text {max}}=\dot{\varepsilon }_3\). Measurements at this rate are used to minimize errors of the stress response due to premature relaxation during the straining prior to reaching the targeted strain levels.

The stress relaxation curves of all three temperatures are combined into an extrapolated single master curve, by means of horizontal shifting (Fig. 6).

Fig. 6
figure 6

Parametrization–identification of the activation energy \(E_{\text {a}}\)

Full size image

A horizontal overlap of the three stress relaxation curves (\(T_{1\dots 3}\)) in Fig. 6 cannot be achieved as a result of the large temperature gap \(\Delta T = {80}\,\hbox {K}\) between each temperature point and chosen holding times of \(t_{\text {h}} = {10}\,\hbox {min}\). However, under the assumption of a monotonically decreasing stiffness on the double logarithmic stiffness-time scale, this shift onto an extrapolated master curve (dotted line) for an identification of the corresponding horizontal shift values is possible.

Solving the Arrhenius equation in Eqs. (23) for the activation energy \(E_{\text {a}}\)

$$\begin{aligned} E_{\text {a}}=\frac{2,303 \text {log}_{10}(a_{\text {T}}) R}{(T_{\text {ref}}-T_{\text {zero}})^{-1}-(T-T_{\text {zero}})^{-1}} \end{aligned}$$
(24)

at both temperature points results in an average activation energy \(E_{\text {a}}\) of 345930 J/mol at a reference temperature of \(T_{\text {ref}} = {23}^{\circ }\hbox {C}\). This result is in line with literature values 328000...657360 J/mol [57] and 292000...1146000 J/mol [58] for epoxy resins.

3.2.2 Identification of Prony-parameters

Multiple approaches to the parametrization of the relaxation spectrum on the basis of experimental results exist. As listed and described in [59], examples for such approaches include Procedure X by Tobolsky [60], the Least Squares Collocation Method, the Window Algorithm by Emri und Tschoegl [61], and the Multi-data Method [59]. Due to the fact that the impact range of individual relaxation strengths \(E_{\text {R},i}\) (2) is limited to the corresponding relaxation times \(\tau _{\text {R},i}\) (3) [49], and because a projected master curve is available, a strict application of either aforementioned calibration method is not necessary. Instead, the relaxation strengths \(E_{\text {R},i}\) from \(i= 1\) to N are sequentially identified starting at the smallest defined relaxation time constant \(\tau _{\text {R},1}\). After successful forecast of the stress relaxation curve between \(t\!=\!0\) and the time constant \(\tau _{\text {R},1}\) belonging to this relaxation strength, the relaxation strength \(E_{\text {R},2}\) at the next consecutive time constant \(\tau _{\text {R},2}\) is parametrized, and so on, until the stress relaxation curve of the element resembles the projected master curve (Fig. 6). Figure 7 gives a comparison between experiment and the initial model response (dashed line) as parametrized by the projected master curve for the temperatures \(T_1\), \(T_2\), and \(T_3\).

Fig. 7
figure 7

Material model parametrization—comparison between experiment, intermediate model response and final model response of step relaxation tests with intermediate unloading at a displacement rate \(\dot{u}_3 = {50}\,\hbox {mm/min}\) for the temperatures \({20}^{\circ }\hbox {C}\), \({100}^{\circ }\hbox {C}\), and \({180}^{\circ }\hbox {C}\)

Full size image

Two systematic mismatches between experiment and initial model response are apparent in Fig. 7. Firstly, the initial stiffness of each experimental run is lower than predicted. This is indicated by the stress curve of the initial response when compared to the cross marks representing experimentally identified values. The initial stress relaxation curve lies below the experimental stresses, which is plausible as additional relaxation occurs prior to reaching the target strain. This was not taken into account during the initial parametrization based on the projected master curve. An elimination of this phenomenon during the experimental characterization is not possible. The second systematic mismatch between experiment and model response is the inaccurate prediction of the material’s base stiffness at elevated temperatures. This is a result of the linear relationship between temperature and the horizontal shift on the logarithmic time scale as governed by the Arrhenius shift function in Eq. (23). Miniature Fig. 6 exemplifies this difference between actual and average activation energy, which results in too high of an adjustment for \({100}^{\circ }\hbox {C}\) and too low of an adjustment for \({180}^{\circ }\hbox {C}\).

On the basis of these results, the relaxation strength spectrum is adjusted using the previously described systematic approach, until the model prediction best matches the experimental stress relaxation curves in Fig. 7 (full line). The prediction of the experimental curves is now significantly improved in comparison with the initial model response, as can be seen in Fig. 7.

The resulting relaxation strength adjustment from the initially projected master curve to the finally parametrized curve of the stress relaxation spanning 28 time decades is displayed in Figs. 7 and 8a.

3.2.3 Transversal contraction parametrization

Experimental results for purely deviatoric or hydrostatic stress relaxation behavior are not available.

Fig. 8
figure 8

Final result–time-temperature master curves

Full size image

The distribution of stiffness \(E_{\text {R}}\) as a result of the stress relaxation behavior into their respective deviatoric and volumetric components G and K is therefore carried out by use of the Poisson’s ratio \(\nu\). The measured Poisson’s ratios at temperatures of \({-40}^{\circ }\hbox {C}\), \({23}^{\circ }\hbox {C}\), and \({180}^{\circ }\hbox {C}\) (Section 2.4.3) indicate a linear trend between temperature and transversal contraction behavior. For the target temperature range, i.e., temperatures below glass transition temperature, this observation is in line with literature findings for expoy resins [51]. In order to identify the Poisson ratio’s time and temperature dependence, an Arrhenius-based time-temperature master curve is created using the previously identified activation energy \(E_{\text {a}}\) of 345930 J/mol and linear interpolation on the logarithmic time scale in between experimentally identified data points (Fig. 8b). The assumption of its validity is based on the literature findings, according to which the horizontal shift factor for the Poisson’s ratio is identical to the shift factor for a material’s stiffness [53].

3.2.4 Volumetric expansion parametrization

The coefficient of thermal expansion is identified for the target temperature range (Fig. 4) and interpolated linearly between characteristic data points to facilitate discretization of the curve without loss of information. The material expansion is simulation step-dependent, as the curing step includes the superimposed chemical contraction component (Sect. 2.4.3). This chemical shrinkage can only be derived during curing shrinkage analysis by subtraction of the known coefficient of thermal expansion (Fig. 4) if the material’s gelation temperature \(T_{\text {gel}}\) is known. \(T_{\text {gel}}\) signifies the temperature, at which the curing-related conversion (monomer cross-linking) has turned the initial potting liquid into a solid. It is only after this point that strains can result in stresses.

As depicted in Fig. 9a, the initial exothermic reaction is measured at \({131,1}^{\circ }\hbox {C}\), with the highest heat flow rate registered at \({137,4}^{\circ }\hbox {C}\). The area below the resulting heat flow curve can be used to indicate the degree of conversion. A conversion percentage of 80% is considered necessary to form a complete cross-linked network, i.e., to call the material a solid. This percentage is reached during DSC at \({156,5}^{\circ }\hbox {C}\). However, the initial exothermic reaction is registered at a much lower temperature of \({131,1}^{\circ }\hbox {C}\), and the material is kept at a constant \({140}^{\circ }\hbox {C}\) for 1 h (Fig. 9b). It is therefore assumed, that the material conversion will have advanced enough to turn solid. This temperature is thus defined as the gelation temperature. The test specimen deflection is modified accordingly by adjustment of the model’s coefficient of expansion until the displacement due to bending in the FE model that matches the measured deflection (Fig. 9c).

Fig. 9
figure 9

Parametrization—effective curing shrinkage, a DSC conversion, b temperature profile and c simulated deflection

Full size image

3.3 Results and model validation

Fig. 10
figure 10

Material model validation—comparison between the experimental results of step relaxation tests with intermediate unloading and the model prediction for the displacement rates \(\dot{u}_1 = {0,5}\,\hbox {mm/min}\) and \(\dot{u}_2 = {5}\,\hbox {mm/min}\) at the temperatures \(T_1 = {23}^{\circ }\hbox {C}\), \(T_2= {100}^{\circ }\hbox {C}\), and \(T_3 = {180}^{\circ }\hbox {C}\)

Full size image

The material model is validated using step relaxation tests with intermediate unloading at strain rates \(\dot{\varepsilon }_{1,2}\) \(\ne\) \(\dot{\varepsilon }_{\text {max}}\). Experimental results making use of these strain rates were explicitly not used during the parametrization process. The comparison between experimental results and the model prediction for all three temperatures \(T_{1\dots 3}\) is shown in Fig. 10.

The model prediction is in agreement with the experimental results. A deviation in curve compliance is most noticeable at high strains \(\varepsilon _4\) near the material strain limit \(\varepsilon _{\text {zB}}\). In that range, the predicted material stiffness is generally overestimated. Similar behavior was previously observed during the comparisons between experimental results and model prediction, when used to parametrize the material model (Fig. 7). Due to the extremely brittle nature of the material, the precondition of linear viscoelastic material behavior is most likely not met at the most severe strains. In addition, the predicted material stiffness at ambient temperature at the strain rate \(\dot{\varepsilon }_2\) is systematically underpredicted. Due to the complex loading scheme of the step relaxation tests with intermediate unloading, no definite explanation can be given.

4 Conclusions

The characterization results indicated linear viscoelastic material behavior for all strain amplitudes. A direct comparison between testing results at different strain rates yielded a comparatively small rate dependency. Most noteworthy, the Poisson’s ratio was lower than expected, while the compressive-to-tensile strength ratio was very large when compared to unfilled epoxy resins. This is especially relevant regarding future strength evaluations, as the strength ratio can be used for calibration of the parabolic failure criterion, a popular criterion for the assessment of polymers [38, 42, 43, 62,63,64,65,66,67,68,69]. Based on the characterization of thermo-mechanically relevant material properties, an approach based on rheological models was used to derive and implement a linear thermo-viscoelastic material model. The fully parametrized material model was successfully validated using step relaxation tests with intermediate unloading with lower strain rates (\(\dot{\varepsilon }_1\), \(\dot{\varepsilon }_2\)). Restrictions to the chosen material model are found in the assumption of a linear viscoelasticity. It is limited to loads as defined by the testing parameters in the experimental characterization testing setup. In addition, time-temperature superposition for both material stiffness and the Poisson’s ratio is assumed to be ideally represented by means of the Arrhenius shift function throughout the entire temperature range. Especially the approaches to and computations of viscoelastic Poisson’s ratios vary significantly throughout literature [70].