SpringerLink
Log in

NSGA-II-TLQR Control of Semi-active Suspension System with Magnetorheological Damper Considering Response Time Delay

  • Original Paper
  • Published:
Journal of Vibration Engineering & Technologies Aims and scope Submit manuscript

Abstract

Purpose

With the advantages of simple structure, low energy consumption, and wide controllable dam** range of magnetorheological (MR) damper, semi-active suspension with MR damper has become a promising application in the existing vehicle suspension system. However, the response time of MR fluid, the operation time of control system and the driving time of MR damper will result in response time delay together, which severe affect the vibration attenuating performance of the vehicle semi-active suspension system with MR damper. In this paper, a LQR controller incorporating NAGA-II algorithm considering response time delay (NSGA-II-TLQR) was developed to compensate for the response time delay of vehicle semi-active suspension system.

Methods

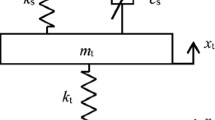
Firstly, the mechanical property experiments of MR damper were carried out, and the direct model and the inverse model of MR damper were established by using genetic algorithm, respectively. Secondly, the model of a two-degree-of-freedom (2DOF) quarter vehicle semi-active suspension system with MR damper was built. Subsequently, the NSGA-II algorithm was introduced to optimize the weighting coefficient matrix of the LQR controller. Then the first-order Taylor series expansion was applied to the NSGA-II-LQR controller to predict the control force, which compensate for the response time delay. Finally, the performance was verified by simulation and experimental tests.

Results

The results show that the body acceleration RMS values with NSGA-II-TLQR controller are decreased by 15.5% and 4.48%, the suspension deflection RMS values are decreased by 22.54% and − 1.22%, and the tire dynamic load RMS values are decreased by 10.32% and 5.38% compared with the passive suspension and the suspension with NSGA-II-LQR controller, respectively.

Conclusions

The semi-active suspension with NSGA-II-TLQR controller has better performance in the ride comfort and handling stability.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21

Similar content being viewed by others

Data availability

The data used to support the findings of this study are available from the corresponding author upon request.

References

  1. Hu G, Ying S, Qi H, Yu L, Li G (2023) Design, analysis and optimization of a hybrid fluid flow magnetorheological damper based on multiphysics coupling model. Mech Syst Signal Process 205:110877

    Article  Google Scholar 

  2. Yang J, Ning D, Sun S, Zheng J, Lu H, Nakano M, Zhang S, Du H, Li W (2021) A semi-active suspension using a magnetorheological damper with nonlinear negative-stiffness component. Mech Syst Signal Process 147:107071

    Article  Google Scholar 

  3. Yu Y, Royel S, Li Y, Li J, Yousefi AM, Gu X, Li S, Li H (2020) Dynamic modelling and control of shear-mode rotational MR damper for mitigating hazard vibration of building structures. Smart Mater Struct 29:114006

    Article  Google Scholar 

  4. Weber F, Maślanka M (2013) Precise stiffness and dam** emulation with MR dampers and its application to semi-active tuned mass dampers of Wolgograd Bridge. Smart Mater Struct 23:015019

    Article  Google Scholar 

  5. Tseng HE, Hrovat D (2015) State of the art survey: active and semi-active suspension control. Veh Syst Dyn 53:1034–1062

    Article  Google Scholar 

  6. Hu G, Liu Q, Ding R, Li G (2017) Vibration control of semi-active suspension system with magnetorheological damper based on hyperbolic tangent model. Adv Mech Eng 9:1–15

    Article  Google Scholar 

  7. Li G, Ruan Z, Gu R, Hu G (2021) Fuzzy sliding mode control of vehicle magnetorheological semi-active air suspension. Appl Sci 11:10925

    Article  Google Scholar 

  8. Ding R, Wang R, Meng X, Chen L (2023) Research on time-delay-dependent H∞/H2 optimal control of magnetorheological semi-active suspension with response delay. J Vib Control 29:1447–1458

    Article  Google Scholar 

  9. Hu G, Zhou F, Yang X, Wang N, Yu L, Li G (2024) Analysis of pressure drop and response characteristics of an enhanced radial magnetorheological valve based on magneto-fluidic coupling. J Magn Magn Mater 589:171589

    Article  Google Scholar 

  10. Karnopp D, Crosby MJ, Harwood RA (1974) Vibration control using semi-active force generators. ASME Pap 122:619–626

    Google Scholar 

  11. Savaresi SM, Silani E, Bittanti S (2005) Acceleration-Driven-Damper (ADD): An optimal control algorithm for comfort-oriented semiactive suspensions. J Dyn Syst Meas Control 127:218–229

    Article  Google Scholar 

  12. Poussot-vassal C, Sename O, Dugard L, Dugard L, Gaspar P, Szabo Z, Bokor J (2007) A LPV based semi-active suspension control strategy. IFAC Proc Vol 40:106–111

    Article  Google Scholar 

  13. Choi SB, Choi JH, Lee YS, Han MS (2003) Vibration control of an ER seat suspension for a commercial vehicle. J Dyn Syst Meas Control 125:60–68

    Article  Google Scholar 

  14. Koch G, Kloiber T (2014) Driving state adaptive control of an active vehicle suspension system. IEEE Trans Control Syst Technol 22:44–57

    Article  Google Scholar 

  15. Li G, Huang Q, Hu G, Ding R, Zhu W, Zeng L (2023) Semi-active fuzzy cooperative control of vehicle suspension with a magnetorheological damper. J Intell Mater Syst Struct 34:2106–2123

    Article  Google Scholar 

  16. Cha Y, Agrawal AK, Dyke SJ (2012) Time delay effects on large-scale MR damper based semi-active control strategies. Smart Mater Struct 22:015011

    Article  Google Scholar 

  17. Yan G, Fang M, Xu J (2019) Analysis and experiment of time-delayed optimal control for vehicle suspension system. J Sound Vib 446:144–158

    Article  Google Scholar 

  18. Mirzal A (2017) Delay compensation using the smith predictor: a brief review with numerical examples. Int J Comput-Aided Mech Des Implement 3:1–8

    Google Scholar 

  19. Pang H, Fu W, Liu K (2015) Stability analysis and fuzzy smith compensation control for semi-active suspension systems with time delay. J Intell Fuzzy Syst 29:2513–2525

    Article  Google Scholar 

  20. Li H, **g X, Karimi H (2013) Output-feedback-based H∞ control for vehicle suspension systems with control delay. IEEE Trans Ind Electron 61:436–446

    Article  Google Scholar 

  21. Dong X, Fei Z, Zhang Z, Deng X, Li P, Liu Q (2023) Gray skyhook predictive control of magnetorheological semi-active seat suspension with time delay. Smart Mater Struct 32:115010

    Article  Google Scholar 

  22. Huang D, Zhang J, Liu Y (2018) The PID semi-active vibration control on nonlinear suspension system with time delay. Int J Intell Transp Syst Res 16:125–137

    Google Scholar 

  23. Tao L, Chen S, Fang G, Zu G (2019) Smith predictor-Taylor series-based LQG control for time delay compensation of vehicle semiactive suspension. Shock Vib 2019:3476826

    Google Scholar 

  24. Wang J, Lv L, Ren J, Chen S (2022) Time delay compensation control using a Taylor series compound robust scheme for a semi-active suspension with magneto rheological damper. Asian J Control 24:2632–2648

    Article  Google Scholar 

  25. Prabakar RS, Sujatha C, Narayanan S (2013) Response of a quarter car model with optimal magnetorheological damper parameters. J Sound Vib 332:2191–2206

    Article  Google Scholar 

Download references

Acknowledgements

This work was supported by National Natural Science Foundation of China (No. 52165004) and Key Program for International Science and Technology Cooperation Project of Jiangxi Province of China (No. 20232BBH80010).

Author information

Authors and Affiliations

  1. School of Mechatronics and Vehicle Engineering, East China Jiaotong University, Nanchang, 330013, China

    Jiawei Zhang, Guoliang Hu, Cheng Yang, Lifan Yu & Wencai Zhu

  2. School of Mechanical Engineering, Jiangxi Vocational College of Mechanical and Electrical Technology, Nanchang, 330013, China

    Jiawei Zhang

Authors
  1. Jiawei Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Guoliang Hu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Cheng Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Lifan Yu
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Wencai Zhu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Guoliang Hu.

Ethics declarations

Conflict of interest

On behalf of all authors, the corresponding author states that there is no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhang, J., Hu, G., Yang, C. et al. NSGA-II-TLQR Control of Semi-active Suspension System with Magnetorheological Damper Considering Response Time Delay. J. Vib. Eng. Technol. (2024). https://doi.org/10.1007/s42417-024-01448-3

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s42417-024-01448-3

Keywords

Search

Navigation