SpringerLink
Log in

Analyzing and Characterizing the Global Complexity of Bistable Structures Under Simple Harmonic Excitation

  • Original Paper
  • Published:
Journal of Vibration Engineering & Technologies Aims and scope Submit manuscript

Abstract

Purpose

The paper aims to develop a method to analyze and characterize the complexity of periodic excited bistable structures.

Methods

An efficient method is developed based on the compute unified device architecture (CUDA) platform for analyzing the complexity of bistable systems in terms of the characteristics of their periodic response. Also, a new complexity metric, state entropy, is proposed by considering the complexity of both the basin of attraction and the attractor. This metric is well suited to be computed by exploiting the parallelism of the graphics processing unit (GPU).

Results

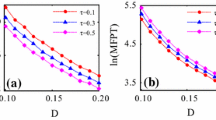
The basins of attraction slices of the system in the three-dimensional state space are plotted by taking a preloaded von Mises truss as an example. Then, the existence of the safety response, steady-state stability, transient stability, and state entropy of the system is calculated for different excitation amplitudes and frequencies.

Conclusion

The proposed method allows an efficient global characterization of bistable systems subject to periodic excitation, and the proposed state entropy is suitable for quantitatively assessing the response complexity of bistable systems.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

Data availability

No data was used for the research described in the article.

References

  1. Liu D, Wu Y, Xu Y, Li J (2019) Stochastic response of bistable vibration energy harvesting system subject to filtered Gaussian white noise. Mech Syst Signal Process 130:201–212

    Article  Google Scholar 

  2. Yang T, Zhou SX, Fang ST, Qin WY, Inman DJ (2021) Nonlinear vibration energy harvesting and vibration suppression technologies: designs, analysis, and applications. Appl Phys Rev 8:031317

    Article  Google Scholar 

  3. Ghouli Z, Litak G (2023) Effect of high-frequency excitation on a bistable energy harvesting system. J Vib Eng Technol 11:99–106

    Article  Google Scholar 

  4. Yan B, Yu N, Ma HY, Wu CY (2022) A theory for bistable vibration isolators. Mech Syst Signal Process 167:108507

    Article  Google Scholar 

  5. Balaji PS, Karthik SelvaKumar K (2021) Applications of nonlinearity in passive vibration control: a review. J Vib Eng Technol 9:183–213

    Article  Google Scholar 

  6. Receveur RAM, Marxer CR, Woering R, Larik VCMH, de Rooij NF (2005) Laterally moving bistable MEMS DC switch for biomedical applications. J Microelectromech Syst 14:1089–1098

    Article  Google Scholar 

  7. Pershin YV, Traversa FL, Di Ventra M (2015) Memcomputing with membrane memcapacitive systems. Nanotechnology 26:225201

    Article  Google Scholar 

  8. Wallin M, Dalklint A, Tortorelli D (2021) Topology optimization of bistable elastic structures—an application to logic gates. Comput Methods Appl Mech Eng 38399:113912

    Article  MathSciNet  Google Scholar 

  9. Daynes S, Nall SJ, Weaver PM, Potter KD, Margaris P, Mellor PH (2010) Bistable composite flap for an airfoil. J Aircr 47(1):334–338

    Article  Google Scholar 

  10. Zhang Z, Li XH, Yu XC, Chai H, Li Y, Wu HP, Jiang SF (2019) Magnetic actuation bionic robotic gripper with bistable morphing structure. Compos Struct 229:111422

    Article  Google Scholar 

  11. Ding SY, Sun M, Li Y, Ma WL, Zhang Z (2022) Novel deployable panel structure integrated with thick origami and morphing bistable composite structures. Materials 15:1942

    Article  Google Scholar 

  12. Wang YZ, Wang Q, Liu MC, Qin YM, Cheng LY, Bolmin O, Alleyne M, Wissa A, Banghman RH, Vella D, Tawfick S (2023) Insect-scale jum** robots enabled by a dynamic buckling cascade. Proc Natl Acad Sci USA 120:e2210651120

    Article  Google Scholar 

  13. Patel DK, Huang XN, Luo YC, Mungekar M, Jawed MK, Yao L, Majidi C (2023) Highly dynamic bistable soft actuator for reconfigurable multimodal soft robots. Adv Mater Technol 8:2201259

    Article  Google Scholar 

  14. Hsu CS (1987) Cell-to-cell map**. A method of global analysis for nonlinear systems. Springer, Berlin

    Google Scholar 

  15. Tongue BH, Gu K (1988) Interpolated cell map** of dynamical systems. J Appl Mech 55:461–466

    Article  MathSciNet  Google Scholar 

  16. Jiang J, Xu JX (1994) A method of point map** under cell reference for global analysis of nonlinear dynamical systems. Phys Lett A 188:137–145

    Article  MathSciNet  Google Scholar 

  17. Hong L, Xu J (2001) Discontinuous bifurcations of chaotic attractors in forced oscillators by generalized cell map** digraph (GCMD) method. Int J Bifur Chaos 11:723–736

    Article  MathSciNet  Google Scholar 

  18. Yue XL, Cui SP, Zhang H, Sun QJ, Xu Y (2021) Generalized cell map** method with deep learning for global analysis and response prediction of dynamical systems. Int J Bifur Chaos 31:2150229

    Article  MathSciNet  Google Scholar 

  19. Datseris G, Wagemakers A (2022) Effortless estimation of basins of attraction. Chaos 32:023104

    Article  MathSciNet  Google Scholar 

  20. Wang XS, Moore SA, Turner JD, Mann BP (2022) A model-free sampling method for basins of attraction using hybrid active learning (HAL). Commun Nonlinear Sci Numer Simul 112:106551

    Article  MathSciNet  Google Scholar 

  21. Belardinelli P, Lenci S (2016) A first parallel programming approach in basins of attraction computation. Int J Non-Linear Mech 80:76–81

    Article  Google Scholar 

  22. Belardinelli P, Lenci S (2016) An efficient parallel implementation of cell map** methods for MDOF systems. Nonlinear Dyn 86:2279–2290

    Article  MathSciNet  Google Scholar 

  23. ** method for global analysis of high-dimensional nonlinear dynamical systems. J Appl Mech 82:111010

    Article  Google Scholar 

  24. Qin ZC, ** method. J Vib Control 23:46–54

    Article  MathSciNet  Google Scholar 

  25. Li ZG, Jiang J, Hong L (2017) Noise-induced transition in a piecewise smooth system by generalized cell map** method with evolving probabilistic vector. Nonlinear Dyn 88:1473–1485

    Article  Google Scholar 

  26. Li QD, Zhou HW, Yang XS (2012) A study of basin of attraction of the simplest walking model based on heterogeneous computation. Acta Phys Sin 61:14–21

    Google Scholar 

  27. Hegedűs F (2021) Program package MPGOS: challenges and solutions during the integration of a large number of independent ODE systems using GPUs. Commun Nonlinear Sci Numer Simul 97:105732

    Article  MathSciNet  Google Scholar 

  28. Nagy D, Plavecz L, Hegedűs F (2022) The art of solving a large number of non-stiff, low-dimensional ordinary differential equation systems on GPUs and CPUs. Commun Nonlinear Sci Numer Simul 112:106521

    Article  MathSciNet  Google Scholar 

  29. Lai Q, Wan Z, Kuate PDK (2022) Generating grid multi-scroll attractors in memristive neural networks. IEEE Trans Circ Syst I Regul Pap 70(3):1324–1336

    Article  Google Scholar 

  30. Lai Q, Chen Z (2023) Grid-scroll memristive chaotic system with application to image encryption. Chaos, Solitons Fractals 170:113341

    Article  MathSciNet  Google Scholar 

  31. Lai Q, Yang L, Liu Y (2022) Design and realization of discrete memristive hyperchaotic map with application in image encryption. Chaos, Solitons Fractals 165:112781

    Article  Google Scholar 

  32. Gelbrecht M, Kurths J, Hellmann F (2020) Monte carlo basin bifurcation analysis. New J Phys 22:033032

    Article  MathSciNet  Google Scholar 

  33. Stender M, Hoffmann N (2022) bSTAB: an open-source software for computing the basin stability of multi-stable dynamical systems. Nonlinear Dyn 107:1451–1468

    Article  Google Scholar 

  34. Daza A, Wagemakers A, Georgeot B, Guery-Odelin D, Sanjuan MAF (2016) Basin entropy: a new tool to analyze uncertainty in dynamical systems. Sci Rep 6:31616

    Article  Google Scholar 

  35. Orlando D, Gonçalves PB, Rega G, Lenci S (2018) Influence of transient escape and added load noise on the dynamic integrity of multistable systems. Int J Non-Linear Mech 109:140–154

    Article  Google Scholar 

  36. Brzeski P, Kurths J, Perlikowski P (2018) Time dependent stability margin in multistable systems. Chaos 28:093104

    Article  MathSciNet  Google Scholar 

  37. Leszczyński M, Perlikowski P, Burzyński T, Kowalski TM, Brzeski P (2022) Review of sample-based methods used in an analysis of multistable dynamical systems. Chaos 32:082101

    Article  MathSciNet  Google Scholar 

  38. Grebogi C, McDonald SW, Ott E, Yorke JS (1983) Final state sensitivity: an obstruction to predictability. Phys Lett A 99:415–418

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

This work is supported by the National Natural Science Foundation of China (12172267).

Author information

Authors and Affiliations

  1. School of Mechano-Electronic Engineering, **dian University, **’an, 710071, China

    Kongming Guo & Yalan Xu

  2. State Key Laboratory for Strength and Vibration, **’an Jiaotong University, **’an, 710049, China

    Jun Jiang

Authors
  1. Kongming Guo
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jun Jiang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yalan Xu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Kongming Guo.

Ethics declarations

Conflict of interest

The authors declare that they have no conflicts of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Guo, K., Jiang, J. & Xu, Y. Analyzing and Characterizing the Global Complexity of Bistable Structures Under Simple Harmonic Excitation. J. Vib. Eng. Technol. 12, 6401–6411 (2024). https://doi.org/10.1007/s42417-023-01259-y

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s42417-023-01259-y

Keywords

Search

Navigation