SpringerLink
Log in

Multiscroll Chaos and Extreme Multistability of Memristive Chaotic System with Application to Image Encryption

  • Original Paper
  • Published:
Journal of Vibration Engineering & Technologies Aims and scope Submit manuscript

Abstract

Purpose

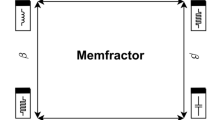
Memristor has attracted extensive research interest and hot discussions in recent years. This paper reports new chaotic system with non-ideal memristor whose internal state is determined by extensible piecewise-linear function, and investigates the application of this system to image encryption.

Methods

Its stabilities of equilibria and complex dynamics are studied. With the change of parameter, the coexisting double-scroll attractors will degenerate into coexisting periodic attractors via bifurcation and split into double number of coexisting single-scroll attractors.

Results

The system can generate multiscroll attractors with any number of scrolls and are easily broken into any number of coexisting double-scroll attractors. This suggests that the introduction of the memristor can enable chaotic system to exhibit more complex and diverse dynamic behaviors.

Conclusions

NIST test and circuit realization are given to verify its physical existence and engineering applicability. In addition, a comprehensive evaluation of the designed efficient chaos-based image encryption algorithm verifies its ability to effectively protect the confidentiality and privacy of image contents.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price includes VAT (Germany)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20

Similar content being viewed by others

Data Availability

All data generated or analyzed during this study are included in this published article.

References

  1. Lorenz EN (1963) Deterministic non-periodic flow. J Atmos Sci 20:130–141

    Article  Google Scholar 

  2. Ojoniyi OS, Njah AN (2016) A 5D hyperchaotic Sprott B system with coexisting hidden attractors. Chaos Solit Fract 87:172–181

    Article  MathSciNet  Google Scholar 

  3. Lai Q, Yang L (2023) A new 3-D memristive hyperchaotic map with multi-parameter-relied dynamics. IEEE Trans Circuits Syst II Express Briefs 70:1625–1629

    Google Scholar 

  4. Elwakil AS, Ozoguz S (2006) Multiscroll chaotic oscillators: the nonautonomous approach. IEEE Trans Circuits Syst II Express Briefs 53:862–866

    Article  Google Scholar 

  5. Mompo E, Carretero M, Bonilla LL (2021) Designing hyperchaos and intermittency in semiconductor superlattices. Phys Rev Lett 127:096601

    Article  Google Scholar 

  6. Ramamoorthy R, Rajagopal K, Leutcho GD, Krejcar O, Namazi H, Hussain I (2022) Multistable dynamics and control of a new 4D memristive chaotic Sprott B system. Chaos Solit Fract 156:111834

    Article  Google Scholar 

  7. Wang R, Li CB, Kong S, Jiang Y, Lei T (2022) A 3D memristive chaotic system with conditional symmetry. Chaos Solit Fract 158:111992

    Article  Google Scholar 

  8. Lai Q, Wan Z, Kuate PDK (2023) Generating grid multi-scroll attractors in memristive neural networks. IEEE Trans Circuits Syst I: Regular Papers 70:1324–1336

    Article  Google Scholar 

  9. Lai Q, Lai C, Zhang H, Li CB (2022) Hidden coexisting hyperchaos of new memristive neuron model and its application in image encryption. Chaos Solit Fract 158:112017

    Article  MathSciNet  Google Scholar 

  10. Wang C, **a H, Zhou L (2017) A memristive hyperchaotic multiscroll Jerk system with controllable scroll numbers. Int J Bifurc Chaos 27:175091

    Article  MathSciNet  Google Scholar 

  11. Yu F, Shen H, Zhang Z, Huang Y, Cai S, Du S (2021) A new multi-scroll Chua’s circuit with composite hyperbolic tangent-cubic nonlinearity: complex dynamics, hardware implementation and image encryption application. Integration 81:71–83

    Article  Google Scholar 

  12. Lai Q, Wan Z, Zhang H, Chen G (2022) Design and analysis of multiscroll memristive Hopfield neural network with adjustable memductance and application to image encryption. IEEE Trans Neural Netw Learn Syst. https://doi.org/10.1109/TNNLS.2022.3146570

    Article  Google Scholar 

  13. Matthews R (1989) On the derivation of a “chaotic’’ encryption algorithm. Cryptologia 8:29–42

    Article  MathSciNet  Google Scholar 

  14. Gao X, Mou J, **ong L, Sha Y, Yan H, Cao Y (2022) A fast and efficient multiple images encryption based on single-channel encryption and chaotic system. Nonlinear Dyn 108:613–636

    Article  Google Scholar 

  15. Norouzi B, Mirzakuchaki S (2014) A fast color image encryption algorithm based on hyper-chaotic systems. Nonlinear Dyn 78:995–1015

    Article  Google Scholar 

  16. Lai Q, Hu G, Erkan U, Toktas A (2023) A novel pixel-split image encryption scheme based on 2D Salomon map. Expert Syst Appl 213:118845

    Article  Google Scholar 

  17. Tsafack N, Iliyasu AM, Dieu NJ, Zeric NJ, Kengne J, Abd-El-Atty B, Belazii A, El-Latif AA (2021) A memristive RLC oscillator dynamics applied to image encryption. J Inform Secur Appl 61:102944

    Google Scholar 

  18. Ouyang X, Luo Y, Liu J, Cao L, Liu Y (2020) A color image encryption method based on memristive hyperchaotic system and DNA encryption. Int J Mode Phys B 34:2050014

    Article  MathSciNet  Google Scholar 

  19. Lai Q, Yang L, Liu Y (2022) Design and realization of discrete memristive hyperchaotic map with application in image encryption. Chaos Solit Fract 165:112781

    Article  Google Scholar 

  20. Li CB, Sprott JC (2016) Variable-boostable chaotic flows. Optik 127:10389–10398

    Article  Google Scholar 

  21. Xu L, Li Z, Li J, Hua W (2016) A novel bit-level image encryption algorithm based on chaotic maps. Opt Lasers Eng 78:17–25

    Article  Google Scholar 

  22. Zhu H, Zhao Y, Song Y (2019) 2D logistic-modulated-sine-coupling-logistic chaotic map for image encryption. IEEE Access 7:14081–14098

    Article  Google Scholar 

  23. Wang X, Guan N, Yang J (2021) Image encryption algorithm with random scrambling based on one-dimensional logistic self-embedding chaotic map. Chaos Solit Fract 150:111117

    Article  MathSciNet  Google Scholar 

  24. Zhou Y, Bao L, Chen CLP (2013) Image encryption using a new parametric switching chaotic system. Signal Process 93:3039–3052

    Article  Google Scholar 

  25. Huang L, Cai S, **ong X, **ao M (2019) On symmetric color image encryption system with permutation-diffusion simultaneous operation. Opt Lasers Eng 115:7–20

    Article  Google Scholar 

Download references

Acknowledgements

This work was supported by the National Natural Science Foundation of China under Grant 61961019, the Key Research and Development Program of Jiangxi Province of China under Grant 20181BBE50017, and the Youth Key Project of Natural Science Foundation of Jiangxi Province of China under Grant 20202ACBL212003.

Author information

Authors and Affiliations

  1. School of Electrical and Automation Engineering, East China Jiaotong University, Nanchang, 330013, China

    Qiang Lai, Yuan Liu & Zhijie Chen

Authors
  1. Qiang Lai
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yuan Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Zhijie Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

All the authors contributed to the study and writing of the manuscript. Conceptualization, methodology, investigation, data collection and analysis were performed by Qiang Lai and Yuan Liu. Visualization and formal analysis were performed by Zhijie Chen.

Corresponding author

Correspondence to Qiang Lai.

Ethics declarations

Conflict of Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this article.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Lai, Q., Liu, Y. & Chen, Z. Multiscroll Chaos and Extreme Multistability of Memristive Chaotic System with Application to Image Encryption. J. Vib. Eng. Technol. 12, 3487–3505 (2024). https://doi.org/10.1007/s42417-023-01060-x

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s42417-023-01060-x

Keywords

Search

Navigation