SpringerLink
Log in

Approximate Solutions of Time-Fractional Swift–Hohenberg Equation via Natural Transform Decomposition Method

  • Original Paper
  • Published:
International Journal of Applied and Computational Mathematics Aims and scope Submit manuscript

Abstract

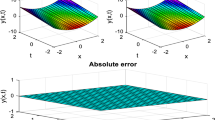
In this study, we apply the natural transform decomposition approach to analyse the time-fractional Swift–Hohenberg problem. The Caputo derivative, a well-known singular kernel derivative, is discussed along with the Caputo–Fabrizio and Atangana–Baleanu derivative in Caputo sense, which are non-singular kernel derivatives. To get the solution, we used the natural transform followed by inverse natural transform. Convergence and uniqueness of the solutions presented. The numerical simulations are offered to guarantee the effectiveness of the method under investigation. The current approach clearly demonstrates how the results for various fractional orders behave. The findings of this study demonstrate the effectiveness and dependability of the suggested method for the analysis of fractional differential equations. The acquired results are compared to the existing solutions numerically and graphically. The results demonstrate the effectiveness, potency, and dependability of the current technique. A variety of partial fractional differential equations can be solved using the presented method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
EUR 32.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or Ebook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

Data Availability

Data sharing is not applicable to this article as no datasets were generated or analysed during the current study.

References

  1. Kumar, D., Seadawy, A.R., Joardar, A.K.: Modified Kudryashov method via new exact solutions for some conformable fractional differential equations arising in mathematical biology. Chin. J. Phys. 56(1), 75–85 (2018)

    Google Scholar 

  2. Baleanu, D., Wu, G.C., Zeng, S.D.: Chaos analysis and asymptotic stability of generalized Caputo fractional differential equations. Chaos, Solitons Fractals 102, 99–105 (2017)

    MathSciNet  MATH  Google Scholar 

  3. Nasrolahpour, H.: A note on fractional electrodynamics. Commun. Nonlinear Sci. Numer. Simul. 18(9), 2589–2593 (2013)

    MathSciNet  MATH  Google Scholar 

  4. Drapaca, C.S., Sivaloganathan, S.: A fractional model of continuum mechanics. J. Elast. 107, 105–123 (2012)

    MathSciNet  MATH  Google Scholar 

  5. Agarwal, P., El-Sayed, A.A.: Non-standard finite difference and Chebyshev collocation methods for solving fractional diffusion equation. Phys. A 500, 40–49 (2018)

    MathSciNet  MATH  Google Scholar 

  6. Prakasha, D.G., Veeresha, P., Rawashdeh, M.S.: Numerical solution for (2+1) dimensional time-fractional coupled Burger equation using fractional natural decomposition method. Math. Methods Appl. Sci. 42(1), 1–19 (2019)

    MathSciNet  MATH  Google Scholar 

  7. Alqahtani, R.T., Ahmad, S., Akgül, A.: Dynamical analysis of bio-ethanol production model under generalized nonlocal operator in Caputo sense. Mathematics 9(19), 2370 (2021)

    Google Scholar 

  8. Ray, S.S., Bera, R.K.: Analytical solution of the Bagley Torvik equation by Adomian decomposition method. Appl. Math. Comput. 168(1), 398–410 (2005)

    MathSciNet  MATH  Google Scholar 

  9. Kumar, D., Tchier, F., Singh, J., Baleanu, D.: An efficient computational technique for fractal vehicular traffic flow. Entropy 20(4), 259 (2018)

    Google Scholar 

  10. Meerschaert, M.M., Tadjeran, C.: Finite difference approximations for two-sided space-fractional partial differential equations. Appl. Numer. Math. 56(1), 80–90 (2006)

    MathSciNet  MATH  Google Scholar 

  11. Safari, M., Ganji, D.D., Moslemi, M.: Application of He’s variational iteration method and Adomian’s decomposition method to the fractional KdV–Burgers–Kuramoto equation. Comput. Math. Appl. 58(11–12), 2091–2097 (2009)

    MathSciNet  MATH  Google Scholar 

  12. Kumar, D., Singh, J., Baleanu, D., Rathore, S.: Analysis of a fractional model of the Ambartsumian equation. Eur. Phys. J. Plus 133(7), 1–7 (2018)

    Google Scholar 

  13. Zhang, X., Zhao, J., Liu, J., Tang, B.: Homotopy perturbation method for two dimensional time-fractional wave equation. Appl. Math. Model. 38(23), 5545–5552 (2014)

    MathSciNet  MATH  Google Scholar 

  14. Baitiche, Z., Derbazi, C., Alzabut, J., Samei, M.E., Kaabar, M.K., Siri, Z.: Monotone iterative method for ψ-Caputo fractional differential equation with nonlinear boundary conditions. Fract. Fract. 5(3), 81 (2021)

    Google Scholar 

  15. Liao, S.: On the homotopy analysis method for nonlinear problems. Appl. Math. Comput. 147(2), 499–513 (2004)

    MathSciNet  MATH  Google Scholar 

  16. Singh, J., Kumar, D., Baleanu, D., Rathore, S.: An efficient numerical algorithm for the fractional Drinfeld–Sokolov–Wilson equation. Appl. Math. Comput. 335, 12–24 (2018)

    MathSciNet  MATH  Google Scholar 

  17. Ahmad, S., Ullah, A., Akgül, A., Jarad, F.: A hybrid analytical technique for solving nonlinear fractional order PDEs of power law kernel: application to KdV and Fornberg–Witham equations. AIMS Math. 7(5), 9389–9404 (2022)

    MathSciNet  Google Scholar 

  18. Haq, I.U., Ali, N., Ahmad, S., Akram, T.: A hybrid interpolation method for fractional PDEs and its applications to fractional diffusion and Buckmaster equations. Math. Probl. Eng. 6(66), 2022 (2022)

    Google Scholar 

  19. Ullah, A., Ullah, A., Ahmad, S., Haq, M.U., Shah, K., Mlaiki, N.: Series type solution of fuzzy fractional order Swift–Hohenberg equation by fuzzy hybrid Sumudu transform. Math. Probl. Eng. 6, 66 (2022)

    Google Scholar 

  20. Hajiseyedazizi, S.N., Samei, M.E., Alzabut, J., Chu, Y.M.: On multi-step methods for singular fractional q-integro-differential equations. Open Math. 19(1), 1378–1405 (2021)

    MathSciNet  MATH  Google Scholar 

  21. Ahmadian, A., Rezapour, S., Salahshour, S., Samei, M.E.: Solutions of sum-type singular fractional q integro-differential equation with m-point boundary value problem using quantum calculus. Math. Methods Appl. Sci. 43(15), 8980–9004 (2020)

    MathSciNet  MATH  Google Scholar 

  22. Rezapour, S., Samei, M.E.: On the existence of solutions for a multi-singular pointwise defined fractional q-integro-differential equation. Bound. Value Probl. 2020(1), 1–33 (2020)

    MathSciNet  MATH  Google Scholar 

  23. Swift, J., Hohenberg, P.C.: Hydrodynamic fluctuations at the convective instability. Phys. Rev. A 15(1), 319 (1977)

    Google Scholar 

  24. Lega, J., Moloney, J.V., Newell, A.C.: Swift–Hohenberg equation for lasers. Phys. Rev. Lett. 73(22), 2978 (1994)

    Google Scholar 

  25. Pomeau, Y., Zaleski, S., Manneville, P.: Dislocation motion in cellular structures. Phys. Rev. A 27(5), 2710 (1983)

    MathSciNet  Google Scholar 

  26. Peletier, L.A., Rottschäfer, V.: Large time behaviour of solutions of the Swift–Hohenberg equation. C.R. Math. 336(3), 225–230 (2003)

    MathSciNet  MATH  Google Scholar 

  27. Ryabov, P.N., Kudryashov, N.A.: Nonlinear waves described by the generalized Swift–Hohenberg equation. J. Phys. Conf. Ser. 788(1), 012032 (2017)

    Google Scholar 

  28. Ahmadian, A., Ismail, F., Salahshour, S., Baleanu, D., Ghaemi, F.: Uncertain viscoelastic models with fractional order: a new spectral tau method to study the numerical simulations of the solution. Commun. Nonlinear Sci. Numer. Simul. 53, 44–64 (2017)

    MathSciNet  MATH  Google Scholar 

  29. Fife, P.C.: Pattern formation in gradient systems. In: Handbook of Dynamical Systems, vol. 2, pp. 677–722. Elsevier (2002)

  30. Hoyle, R., Hoyle, R.B.: Pattern formation: an introduction to methods. Cambridge University Press, Cambridge (2006)

    MATH  Google Scholar 

  31. Vishal, K., Kumar, S., Das, S.: Application of homotopy analysis method for fractional Swift–Hohenberg equation–revisited. Appl. Math. Model. 36(8), 3630–3637 (2012)

    MathSciNet  MATH  Google Scholar 

  32. Khan, N.A., Khan, N.U., Ayaz, M., Mahmood, A.: Analytical methods for solving the time-fractional Swift–Hohenberg (S–H) equation. Comput. Math. Appl. 61(8), 2182–2185 (2011)

    MathSciNet  MATH  Google Scholar 

  33. Merdan, M.: A numeric–analytic method for time-fractional Swift–Hohenberg (S–H) equation with modified Riemann–Liouville derivative. Appl. Math. Model. 37(6), 4224–4231 (2013)

    MathSciNet  MATH  Google Scholar 

  34. Vishal, K., Das, S., Ong, S.H., Ghosh, P.: On the solutions of fractional Swift–Hohenberg equation with dispersion. Appl. Math. Comput. 219(11), 5792–5801 (2013)

    MathSciNet  MATH  Google Scholar 

  35. Alrabaiah, H., Ahmad, I., Shah, K., Mahariq, I., Rahman, G.U.: Analytical solution of non-linear fractional order Swift–Hohenberg equations. Ain Shams Eng. J. 12(3), 3099–3107 (2021)

    Google Scholar 

  36. Attia, N., Akgül, A., Seba, D., Nour, A.: Numerical solutions to the time-fractional Swift–Hohenberg equation using reproducing kernel Hilbert space method. Int. J. Appl. Comput. Math 7, 194 (2021)

    MathSciNet  MATH  Google Scholar 

  37. McCalla, S., Sandstede, B.: Snaking of radial solutions of the multi-dimensional Swift–Hohenberg equation: a numerical study. Phys. D 239(16), 1581–1592 (2010)

    MathSciNet  MATH  Google Scholar 

  38. Kudryashov, N.A., Sinelshchikov, D.I.: Exact solutions of the Swift–Hohenberg equation with dispersion. Commun. Nonlinear Sci. Numer. Simul. 17(1), 26–34 (2012)

    MathSciNet  MATH  Google Scholar 

  39. Prakasha, D.G., Veeresha, P., Baskonus, H.M.: Residual power series method for fractional Swift–Hohenberg equation. Fract. Fract. 3(1), 9 (2019)

    Google Scholar 

  40. Li, W., Pang, Y.: An iterative method for time-fractional Swift–Hohenberg equation. Adv. Math. Phys. 6, 66 (2018)

    MathSciNet  MATH  Google Scholar 

  41. Rawashdeh, M.S., Maitama, S.: Solving coupled system of nonlinear PDE’s using the natural decomposition method. Int. J. Pure Appl. Math. 92(5), 757–776 (2014)

    Google Scholar 

  42. Rawashdeh, M.S., Maitama, S.: Solving nonlinear ordinary differential equations using the NDM. J. Appl. Anal. Comput 5(1), 77–88 (2015)

    MathSciNet  MATH  Google Scholar 

  43. Rawashdeh, M., Maitama, S.: Finding exact solutions of nonlinear PDEs using the natural decomposition method. Math. Methods Appl. Sci. 40(1), 223–236 (2017)

    MathSciNet  MATH  Google Scholar 

  44. Eltayeb, H., Abdalla, Y.T., Bachar, I., Khabir, M.H.: Fractional telegraph equation and its solution by natural transform decomposition method. Symmetry 11(3), 334 (2019)

    MATH  Google Scholar 

  45. Cherif, M.H., Ziane, D., Belghaba, K.: Fractional natural decomposition method for solving fractional system of nonlinear equations of unsteady flow of a polytropic gas. Nonlinear Stud 25(4), 753–764 (2018)

    MathSciNet  MATH  Google Scholar 

  46. Khan, H., Shah, R., Kumam, P., Arif, M.: Analytical solutions of fractional-order heat and wave equations by the natural transform decomposition method. Entropy 21(6), 597 (2019)

    MathSciNet  Google Scholar 

  47. Shah, R., Khan, H., Mustafa, S., Kumam, P., Arif, M.: Analytical solutions of fractional-order diffusion equations by natural transform decomposition method. Entropy 21(6), 557 (2019)

    MathSciNet  Google Scholar 

  48. Shah, R., Khan, H., Kumam, P., Arif, M., Baleanu, D.: Natural transform decomposition method for solving fractional-order partial differential equations with proportional delay. Mathematics 7(6), 532 (2019)

    Google Scholar 

  49. Zhou, M.X., Kanth, A.S.V., Aruna, K., Raghavendar, K., Rezazadeh, H., Inc, M., Aly, A.A.: Numerical solutions of time fractional Zakharov–Kuznetsov equation via natural transform decomposition method with nonsingular kernel derivatives. J. Funct. Spaces 6, 66 (2021)

    MathSciNet  MATH  Google Scholar 

  50. Kanth, A.R., Aruna, K., Raghavendar, K., Rezazadeh, H., Inc, M.: Numerical solutions of nonlinear time fractional Klein-Gordon equation via natural transform decomposition method and iterative Shehu transform method. J. Ocean Eng. Sci. 6, 66 (2021)

    Google Scholar 

  51. Mohamed, M.S., Gepreel, K.A.: Numerical solutions for the time fractional variant Bussinesq equation by homotopy analysis method. Sci. Res. Essays 8(44), 2163–2170 (2013)

    Google Scholar 

  52. Caputo, M., Fabrizio, M.: A new definition of fractional derivative without singular kernel. Progr. Fract. Differ. Appl. 1(2), 73–85 (2015)

    Google Scholar 

  53. Atangana, A., Baleanu, D.: New fractional derivatives with nonlocal and non-singular kernel: theory and application to heat transfer model. Therm. Sci. 20(2), 763–769 (2016)

    Google Scholar 

  54. Khan, Z.H., Khan, W.A.: N-transform properties and applications. NUST J. Eng. Sci. 1(1), 127–133 (2008)

    Google Scholar 

  55. Loonker, D., Banerji, P.K.: Solution of fractional ordinary differential equations by natural transform. Int. J. Math. Eng. Sci. 12(2), 1–7 (2013)

    Google Scholar 

  56. Khalouta, A., Kadem, A.: A new numerical technique for solving fractional Bratu’s initial value problems in the Caputo and Caputo–Fabrizio sense. J. Appl. Math. Comput. Mech. 19(1), 43–56 (2020)

    MathSciNet  MATH  Google Scholar 

  57. Ravi Kanth, A.S.V., Aruna, K., Raghavendar, K.: Numerical solutions of time fractional Sawada Kotera Ito equation via natural transform decomposition method with singular and nonsingular kernel derivatives. Math. Methods Appl. Sci. 44(18), 14025–14040 (2021)

    MathSciNet  MATH  Google Scholar 

  58. Veeresha, P., Prakasha, D.G., Baleanu, D.: Analysis of fractional Swift–Hohenberg equation using a novel computational technique. Math. Meth. Appl. Sci. 43(4), 1970–1987 (2020)

    MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The authors would like to thank the anonymous referees for carefully reading the manuscript and providing valuable feedback.

Funding

There is no funding for this work.

Author information

Authors and Affiliations

  1. Department of Mathematics, School of Advanced Sciences, Vellore Institute of Technology: VIT University, Vellore, Tamil Nadu, India

    K. Pavani & K. Raghavendar

Authors
  1. K. Pavani
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. K. Raghavendar
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

KP: Methodology, Validation, Visualization. KR: Investigation, Methodology, Supervision, Validation, Visualization, Writing original draft.

Corresponding author

Correspondence to K. Raghavendar.

Ethics declarations

Conflict of interest

There is no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Pavani, K., Raghavendar, K. Approximate Solutions of Time-Fractional Swift–Hohenberg Equation via Natural Transform Decomposition Method. Int. J. Appl. Comput. Math 9, 29 (2023). https://doi.org/10.1007/s40819-023-01493-8

Download citation

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40819-023-01493-8

Keywords

Search

Navigation