Analysis of Heatline and Entropy Generation during Magnetohydrodynamic Natural Convection in a Trapezoidal Enclosure

Abstract

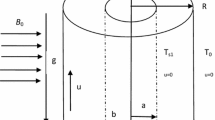
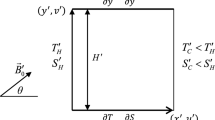
This paper presents an analysis of steady natural convection flow in a trapezoidal enclosure with various aspect ratios in presence of magnetic field applied in the direction perpendicular to the parallel side walls. Two different boundary conditions are considered. In both the cases, bottom wall is uniformly heated, the top wall is insulated and left wall is linearly heated. In case 1, right wall is linearly heated while in case 2, right wall is considered to be cold. The numerical computation is carried out using biharmonic formulation in stream function to find the stream lines, isotherms, heatlines, entropy generation due to heat transfer and entropy generation due to fluid friction, local average Nusselt number and Bejan number. We have obtained these results for various values of the Rayleigh number (Ra), Prandlt number (Pr), Hartman number(Ha), aspect ratios (A) $=0.5,~1.0,~1.5$ and inclination angles of cavity $(\phi )$. It is found that intensity of heat flow decreases as magnetic field parameter increases. It is also observed that the intensity of heat flow increases with the increase in the aspect ratio. Finally, the predicted results for average Nusselt number and Bejan number in both the cases are correlated in terms of the studied parameters.

Appendix

$$\begin{aligned} G= & {} \frac{1}{1+2\eta A \cot \phi },~~E=-2 G \cot \phi (2 \xi -1),~~F = G^{2}[1+ \cot ^{2}\phi (2 \xi -1)^{2}], \\ H= & {} 4 G^{2} \cot ^{2}\phi (2\xi -1),~~ C=-U G+ V G(2\xi -1)\cot \phi + Pr H,\\{} & {} \quad ~~B=U G+ 0.5 V E A-H,\\ T_{1}= & {} -8Pr F G^{2}(1-2\xi )\cot ^{2}\phi +PrFH +F C\\{} & {} - 4 A G^{3}\cot \phi [1+(1-2\xi )^{2}\cot ^{2}\phi ], \\ T_{2}= & {} -\frac{8}{A}Pr F G \cot \phi - 8Pr E G^{2}(1-2\xi )\cot ^{2}\phi \\ {}{} & {} +Pr E H-\frac{8}{A}G^{3} Pr \cot \phi [1+(1-2\xi )^{2}\cot ^{2}\phi ]+C E-\frac{V E}{A}, \\ T_{3}= & {} -\frac{4}{A}Pr E G \cot \phi -\frac{8}{A^{2}}Pr G^{2}(1-2\xi )\cot ^{2}\phi +\frac{Pr H}{A^{2}}+\frac{C}{A^{2}}-\frac{V E}{A}, \\ T_{4}= & {} 24 G^{2}Pr \cot ^{2}\phi +32Pr E G^{3} A(1-2\xi )\cot ^{3}\phi \\{} & {} +24 G^{4} Pr \cot ^{2} \phi [1+(1-2\xi )^{2}\cot ^{2}\phi ] \\{} & {} -4 C G^{2} (1-2\xi )\cot ^{2}\phi +C H+4 VG^{3} \cot \phi [1+(1-2\xi )^{2}\cot ^{2}\phi ], \\ T_{5}= & {} \frac{2 Pr F}{A^{2}}+Pr E^{2}, \\ T_{6}= & {} 16G^{2}Pr E \cot ^{2}\phi +\frac{32}{A}Pr G^{3}(1-2\xi )\cot ^{3}\phi -\frac{4}{A}C G \cot \phi \\{} & {} \quad +\frac{4}{A}V G^{2}(1-2\xi )\cot ^{2}\phi -\frac{V H}{A}, \\ T_{7}= & {} -32Pr E G^{3}A E\cot ^{3}\phi -96Pr G^{4}(1-2\xi )\cot ^{4}\phi +8C G^{2}\cot ^{2}\phi \\{} & {} \quad -16V G^{3}(1-2\xi )\cot ^{3}\phi , \\ \frac{\partial \psi }{\partial \xi }= & {} \frac{1}{2h}(\psi _{i+1,j}-\psi _{i-1,j}) + O(h^{2}),~~ \frac{\partial \psi }{\partial \eta }= \frac{1}{2h}(\psi _{i,j+1}-\psi _{i,j-1})+ O(h^{2}), \\ \frac{\partial ^{2} \psi }{\partial \xi ^{2}}= & {} \frac{1}{h^{2}}(\psi _{i+1,j}-2\psi _{i,j}+\psi _{i-1,j})+ O(h^{2}),\\ \frac{\partial ^{2} \psi }{\partial \eta ^{2}}= & {} \frac{1}{h^{2}}(\psi _{i,j+1}-2\psi _{i,j}+\psi _{i,j-1})+ O(h^{2}), \\ \frac{\partial ^{2} \psi }{\partial \xi \partial \eta }= & {} \frac{1}{4h^{2}}(\psi _{i-1,j-1}-\psi _{i+1,j-1}+\psi _{i+1,j+1}-\psi _{i-1,j+1})+ O(h^{2}), \\ \frac{\partial ^{3} \psi }{\partial \xi ^{2}\partial \eta }= & {} \frac{1}{2h^{3}}(2\psi _{i,j-1}-2\psi _{i,j+1}-\psi _{i-1,j-1}-\psi _{i+1,j-1}\\{} & {} +\psi _{i+1,j+1}+\psi _{i-1,j+1})+ O(h^{2}), \\ \frac{\partial ^{3} \psi }{\partial \xi ^{3}}= & {} \frac{1}{h^{2}}(\psi _{\xi i+1,j}-2\psi _{\xi i,j}+\psi _{\xi i-1,j})+ O(h^{2}),\\ \frac{\partial ^{3} \psi }{\partial \eta ^{3}}= & {} \frac{1}{h^{2}}(\psi _{\eta i,j+1}-2\psi _{\eta i,j}+\psi _{\eta i,j-1})+ O(h^{2}), \\ \frac{\partial ^{3} \psi }{\partial \xi \partial \eta ^{2}}= & {} \frac{1}{2h^{3}}[2\psi _{i-1,j}-2\psi _{i+1,j}-\psi _{i-1,j-1}+\psi _{i+1,j-1}\\{} & {} +\psi _{i+1,j+1}-\psi _{i-1,j+1}]+ O(h^{2}), \\ \frac{\partial ^{4} \psi }{\partial \xi ^{4}}= & {} \frac{6}{h^{4}}[h(\psi _{\xi i+1,j}-\psi _{\xi i-1,j})-2(\psi _{i+1,j}-2\psi _{i,j}+\psi _{i-1,j})]+ O(h^{2}), \\ \frac{\partial ^{4} \psi }{\partial \eta ^{4}}= & {} \frac{6}{h^{4}}[h(\psi _{\eta i,j+1}-\psi _{\eta i,j-1})-2(\psi _{i,j+1}-2\psi _{i,j}+\psi _{i,j-1})]+ O(h^{2}), \\ \frac{\partial ^{4} \psi }{\partial \xi ^{3}\partial \eta }= & {} \frac{1}{2 h^{3}}[2\psi _{\xi i,j-1}-2\psi _{\xi i,j+1}-\psi _{\xi i-1,j-1}-\psi _{\xi i+1,j-1}+\psi _{\xi i+1,j+1}\\{} & {} +\psi _{\xi i-1,j+1}]+ O(h^{2}), \\ \frac{\partial ^{4} \psi }{\partial \xi \partial \eta ^{3}}= & {} \frac{1}{2 h^{3}}[2\psi _{\eta i-1,j}-2\psi _{\eta i+1,j}-\psi _{\eta i-1,j-1}+\psi _{\eta i+1,j-1}\\{} & {} +\psi _{\eta i+1,j+1}-\psi _{\eta i-1,j+1}]+ O(h^{2}), \\ \frac{\partial ^{4} \psi }{\partial \xi ^{2}\partial \eta ^{2}}= & {} \frac{1}{h^{4}}[4\psi _{i,j}-2(\psi _{i-1,j}+\psi _{i+1,j}+\psi _{i,j-1}+\psi _{i,j+1})+\psi _{i-1,j-1} \\ {}{} & {} +\psi _{i+1,j-1}+\psi _{i+1,j+1}-\psi _{i-1,j+1}]+ O(h^{2}). \end{aligned}$$

Here, h is the step length on a uniform rectangular mesh in the transformed domain.