SpringerLink
Log in

Energy stability and convergence of variable-step L1 scheme for the time fractional Swift-Hohenberg model

  • Original Paper
  • Published:
Fractional Calculus and Applied Analysis Aims and scope Submit manuscript

Abstract

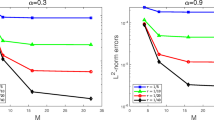
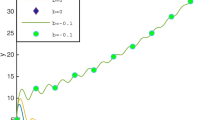
A fully implicit numerical scheme is established for solving the time fractional Swift-Hohenberg equation with a Caputo time derivative of order \(\alpha \in (0,1)\). The variable-step L1 formula and the finite difference method are employed for the time and the space discretizations, respectively. The unique solvability of the numerical scheme is proved by the Brouwer fixed-point theorem. With the help of the discrete convolution form of L1 formula, the time-step** scheme is shown to preserve a discrete energy dissipation law which is asymptotically compatible with the classic energy law as \(\alpha \rightarrow 1^-\). Furthermore, the \(L^\infty \) norm boundedness of the discrete solution is obtained. Combining with the global consistency error analysis framework, the \(L^2\) norm convergence order is shown rigorously. Several numerical examples are provided to illustrate the accuracy and the energy dissipation law of the proposed method. In particular, the adaptive time-step** strategy is utilized to capture the multi-scale time behavior of the time fractional Swift-Hohenberg model efficiently.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
EUR 32.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or Ebook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  1. Swift, J., Hohenberg, P.C.: Hydrodynamic fluctuations at the convective instability. Phys. Rev. A 15(1), 319–328 (1977)

    Article  Google Scholar 

  2. Ibbeken, G., Green, G., Wilczek, M.: Large-scale pattern formation in the presence of small-scale random advection. Phys. Rev. Lett. 123(11), 114501 (2019)

    Article  Google Scholar 

  3. Kudryashov, N.A., Sinelshchikov, D.I.: Exact solutions of the Swift-Hohenberg equation with dispersion. Commun. Nonlinear Sci. Numer. Simulat. 17(1), 26–34 (2012)

    Article  MathSciNet  Google Scholar 

  4. Lega, J., Mendelson, N.H.: Control-parameter-dependent Swift-Hohenberg equation as a model for bioconvection patterns. Phys. Rev. E 59(6), 6267–6274 (1999)

    Article  Google Scholar 

  5. Lee, H.G.: Numerical simulation of pattern formation on surfaces using an efficient linear second-order method. Symmetry 11(8), 1010 (2019)

    Article  Google Scholar 

  6. Rosa, R.R., Pontes, J., Christov, C.I., Ramos, F.M., Rodrigues Neto, C., Rempel, E.L., Walgraef, D.: Gradient pattern analysis of Swift-Hohenberg dynamics: phase disorder characterization. Physica A 283(1–2), 156–159 (2000)

    Article  Google Scholar 

  7. Lee, H.G.: An energy stable method for the Swift-Hohenberg equation with quadratic-cubic nonlinearity. Comput. Methods Appl. Mech. Eng. 343, 40–51 (2019)

    Article  MathSciNet  Google Scholar 

  8. Du, Q., Nicolaides, R.A.: Numerical analysis of a continuum model of phase transition. SIAM J. Numer. Anal. 28(5), 1310–1322 (1991)

    Article  MathSciNet  Google Scholar 

  9. Xu, C., Tang, T.: Stability analysis of large time-step** methods for epitaxial growth models. SIAM J. Numer. Anal. 44(4), 1759–1779 (2006)

    Article  MathSciNet  Google Scholar 

  10. Di, Y., Wei, Y., Zhang, J., Zhao, C.: Sharp error estimate of an implicit BDF2 scheme with variable time steps for the phase field crystal model. J. Sci. Comput. 92(2), 65 (2022)

    Article  MathSciNet  Google Scholar 

  11. Cartea, A., Del-Castillo-Negrete, D.: Fractional diffusion models of option prices in markets with jumps. Physica A 374(1), 749–763 (2007)

    Article  Google Scholar 

  12. Chen, W.: A speculative study of 2/3-order fractional Laplacian modeling of turbulence: Some thoughts and conjectures. Chaos 16(2), 023126 (2006)

    Article  Google Scholar 

  13. Qureshi, S., Yusuf, A., Shaikh, A.A., Inc, M.: Transmission dynamics of varicella zoster virus modeled by classical and novel fractional operators using real statistical data. Physica A 534, 122149 (2019)

    Article  MathSciNet  Google Scholar 

  14. Li, Z., Wang, H., Yang, D.: A space-time fractional phase-field model with tunable sharpness and decay behavior and its efficient numerical simulation. J. Comput. Phys. 347, 20–38 (2017)

    Article  MathSciNet  Google Scholar 

  15. Song, F., Xu, C., Karniadakis, G.E.: A fractional phase-field model for two-phase flows with tunable sharpness: Algorithms and simulations. Comput. Methods Appl. Mech. Engrg. 305, 376–404 (2016)

    Article  MathSciNet  Google Scholar 

  16. Shamseldeen, S.: Approximate solution of space and time fractional higher order phase field equation. Physica A 494, 308–316 (2018)

    Article  MathSciNet  Google Scholar 

  17. Zhao, J., Chen, L., Wang, H.: On power law scaling dynamics for time-fractional phase field models during coarsening. Commun. Nonlinear. Sci. Numer. Simulat. 70, 257–270 (2019)

    Article  MathSciNet  Google Scholar 

  18. Tang, T., Yu, H., Zhou, T.: On energy dissipation theory and numerical stability for time-fractional phase-field equations. SIAM J. Sci. Comput. 41(6), A3757–A3778 (2019)

    Article  MathSciNet  Google Scholar 

  19. Quan, C.Y., Tang, T., Yang, J.: How to define dissipation-preserving energy for time-fractional phase-field equations. CSIAM Trans. Appl. Math. 1(3), 478–490 (2020)

    Article  Google Scholar 

  20. Liao, H.-L., Zhu, X., Wang, J.: The variable-step L1 scheme preserving a compatible energy law for time-fractional Allen-Cahn equation. Numer. Math.-Theory Methods Appl. 15(4), 1128–1146 (2022)

  21. Yang, Y., Wang, J., Chen, Y., Liao, H.-L.: Compatible \(L^2\) norm convergence of variable-step L1 scheme for the time-fractional MBE model with slope selection. J. Comput. Phys. 467, 111467 (2022)

    Article  Google Scholar 

  22. Quan, C.Y., Wang, B.Y.: Energy stable L2 schemes for time-fractional phase-field equations. J. Comput. Phys. 458, 111085 (2022)

    Article  MathSciNet  Google Scholar 

  23. Quan, C. Y., Tang, T., Yang, J.: Numerical energy dissipation for time-fractional phase-field equations. ar**v:2009.06178 (2021)

  24. Veeresha, P., Prakasha, D.G., Baleanu, D.: Analysis of fractional Swift-Hohenberg equation using a novel computational technique. Math. Meth. Appl. Sci. 43(4), 1970–1987 (2020)

    Article  MathSciNet  Google Scholar 

  25. Prakasha, D.G., Veeresha, P., Baskonus, H.M.: Residual power series method for fractional Swift-Hohenberg equation. Fractal Fract. 3(1), 9 (2019)

    Article  Google Scholar 

  26. Merdan, M.: A numeric-analytic method for time-fractional Swift-Hohenberg (S-H) equation with modified Riemann-Liouville derivative. Appl. Math. Model. 37(6), 4224–4231 (2013)

    Article  MathSciNet  Google Scholar 

  27. Khan, N.A., Khan, N.-U., Ayaz, M., Mahmood, A.: Analytical methods for solving the time-fractional Swift-Hohenberg (S-H) equation. Comput. Math. Appl. 61(8), 2182–2185 (2011)

    Article  MathSciNet  Google Scholar 

  28. Rashid, S., Ashraf, R., Bayones, F.S.: A novel treatment of fuzzy fractional Swift-Hohenberg equation for a hybrid transform within the fractional derivative operator. Fractal. Fract. 5(4), 209 (2021)

    Article  Google Scholar 

  29. Zahra, W.K., Elkholy, S.M., Fahmy, M.: Rational spline-nonstandard finite difference scheme for the solution of time-fractional Swift-Hohenberg equation. Appl. Math. Comput. 343, 372–387 (2019)

    MathSciNet  Google Scholar 

  30. Zahra, W.K., Nasr, M.A., Baleanu, D.: Time-fractional nonlinear Swift-Hohenberg equation: Analysis and numerical simulation. Alex. Eng. J. 59(6), 1970–1987 (2020)

    Article  Google Scholar 

  31. Weng, Z., Deng, Y., Zhuang, Q., Zhai, S.: A fast and efficient numerical algorithm for Swift-Hohenberg equation with a nonlocal nonlinearity. Appl. Math. Lett. 118, 107170 (2021)

    Article  MathSciNet  Google Scholar 

  32. Liao, H.-L., Tang, T., Zhou, T.: An energy stable and maximum bound preserving scheme with variable time steps time fractional Allen-Cahn equations. SIAM. J. Sci. Comput. 43(5), A3503–A3526 (2021)

    Article  MathSciNet  Google Scholar 

  33. Akrivis, G.D.: Finite difference discretization of the cubic Schrödinger equation. IMA J. Numer. Anal. 13(1), 115–124 (1993)

    Article  MathSciNet  Google Scholar 

  34. Liao, H.-L., Yan, Y., Zhang, J.: Unconditional convergence of a fast two-level linearized algorithm for semilinear subdiffusion equations. J. Sci. Comput. 80(1), 1–25 (2019)

    Article  MathSciNet  Google Scholar 

  35. Sun, H., Zhao, X., Cao, H., Yang, R., Zhang, M.: Stability and convergence analysis of adaptive BDF2 scheme for the Swift-Hohenberg equation. Commun. Nonlinear Sci. Numer. Simulat. 111, 106412 (2022)

    Article  MathSciNet  Google Scholar 

  36. Stynes, M., O’riordan, E., Gracia, J.L.: Error analysis of a finite difference method on graded meshes for a time-fractional diffusion equation. SIAM. J. Numer. Anal. 55(2), 1057–1079 (2017)

    Article  MathSciNet  Google Scholar 

  37. Li, D., She, M., Sun, H., Zhang, Z.: A novel discrete fractional Grönwall-type inequality and its application in pointwise-in-time error estimates. J. Sci. Comput. 91, 27 (2022)

    Article  Google Scholar 

  38. **, B., Zhou, Z.: Numerical Treatment and Analysis of Time-Fractional Evolution Equations. Springer, Cham (2023)

    Book  Google Scholar 

  39. Mclean, W., Mustapha, K.: A second-order accurate numerical method for a fractional wave equation. Numer. Math. 105(3), 481–510 (2007)

    Article  MathSciNet  Google Scholar 

  40. Jiang, S., Zhang, J., Zhang, Q., Zhang, Z.: Fast evaluation of the Caputo fractional derivative and its applications to fractional diffusion equations. Commun. Comput. Phys. 21(3), 650–678 (2017)

    Article  MathSciNet  Google Scholar 

  41. Yang, J., Kim, J.: Energy dissipation-preserving time-dependent auxiliary variable method for the phase-field crystal and the Swift-Hohenberg models. Numer. Algorithms 89, 1865–1894 (2022)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

We would like to acknowledge support by the National Natural Science Foundation of China (No. U22B2046, 61833005,11701081,11861060), Jiangsu Province Natural Science Foundation(No. BK20222023), High-level Scientific Research foundation for the introduction of talent of Nan**g Institute of Technology (No. YKL201856).

Author information

Authors and Affiliations

  1. School of Mathematics, Southeast University, Nan**g, 210096, People’s Republic of China

    Xuan Zhao, Ran Yang & Ren-jun Qi

  2. Department of Mathematics and Physics, Nan**g Institute of Technology, Nan**g, 211167, People’s Republic of China

    Hong Sun

Authors
  1. Xuan Zhao
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ran Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Ren-jun Qi
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Hong Sun
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Xuan Zhao.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhao, X., Yang, R., Qi, Rj. et al. Energy stability and convergence of variable-step L1 scheme for the time fractional Swift-Hohenberg model. Fract Calc Appl Anal 27, 82–101 (2024). https://doi.org/10.1007/s13540-023-00231-7

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13540-023-00231-7

Keywords

Mathematics Subject Classification

Search

Navigation