Introduction

Generally, weirs are used for measuring and controlling the flow in irrigation, drainage and transmission canals. Weirs can be used on the inlet of canals in various shapes such as triangular, circular and parabolic. Such weirs are made of a vertical sheet embedded on the flow path and have an edge and a relatively sharp crest. In addition to being used as a flow measurement device in an open channel, sharp-edged weirs are also used to increase the height and volume of water upstream and water passes over it. Perhaps, the COD of a spillway is one of the significant factors for the construction this type of hydraulic structures. Due to the high significance of the COD of weirs, many laboratories, analytical and numerical research have been executed on this variable by different researchers. Vatankhah and Khamisabadi (2019) experimentally and theoretically studied sharp-edged weirs. To this end, the spillway and critical flow models were used along with the conduction of a dimensional analysis for the conclusion of the discharge equation of sharp-edged weirs. They also conducted an experimental study for calibrating theoretical formulae in free flow conditions. The proposed equations had errors less than 1.7%. Azimi and Shabanlou (2020) proposed some relations between discharge and geometric and hydraulic properties via the two-dimensional channel outflow theory to compute the discharge of lateral weirs in U-shaped channels for subcritical and supercritical conditions. According to their research, a surface jump along with a stagnation point occurred at the end of the lateral spillway for both conditions. In addition, a secondary flow cell formed after the lateral spillway and extended into the entire downstream direction under subcritical flow conditions. Bagherifar et al. (2020) simulated the changes of inflow free surface, turbulence and flow field passing through a circular channel across a lateral spillway. They showed that the average energy difference in the upstream and downstream of the lateral spillway was obtained to be about 2.1%.

In recent decades, machine learning algorithms have been widely implemented to recreate various phenomena because these tools are sufficiently accurate, affordable and reliable, and able to simulate many linear and nonlinear phenomena (Akhbari et al. 2017; Shabanlou et al. 2018; Azimi and Shiri 2021aEbtehaj 2021).

Ebtehaj et al. (2015a) implemented the Group Method of Data Handling (GMDH) method to predict the COD in lateral weirs. The Froude number, dimensionless length of the spillway, the ratio of the length of the spillway to the depth of the upstream flow and the height of the spillway to its length were input parameters for develo** a model to predict the COD. They showed that the proposed model accurately predicted the COD and this model performed more accurately than the feed-forward neural network model and nonlinear regression equations. Ebtehaj et al. (2015b) utilized the gene expression programming (GEP) approach as a modern technique for approximating the COD of lateral weirs. Firstly, they examined the exactness of the existing equations in computing the COD of lateral weirs. Then, by considering dimensionless parameters influencing this parameter and conducting a sensitivity analysis, they managed to develop five different models. Khoshbin et al. (2016) employed the adaptive neuro-fuzzy inference system (ANFIS) to recreate the COD of rectangular sharp-edged lateral weirs for optimal choose of membership functions, while the Singular Value Decomposition (SVD) approach helped to calculate the linear variables of the ANFIS results section (GA/SVD-ANFIS). The influence of each dimensionless variable on the COD prediction was investigated in five different models to perform the sensitivity analysis by employing the aforementioned dimensionless variables. Azimi et al. (2017) acquired the COD of lateral orifices via the adaptive neural fuzzy inference system (ANFIS) and a combination of ANFIS and the genetic algorithm (ANFIS-GA). Furthermore, they compared the performance of neuro-fuzzy models with a computational fluid dynamics model. The analysis of the simulation results proved that the ANFIS-GA model performed better. Azimi et al. (2019) forecasted the COD of rectangular lateral weirs located in trapezoidal channels via support vector machines (SVM). Six models (SVM 1-SVM 6) were extended on the basis of the impacting variables on the COD of lateral weirs in trapezoidal channels. The ratio of the lateral spillway length to the trapezoidal channel width is detected as the most impacting input variable for the COD modeling. They presented a matrix for the superior model for computing the COD of lateral weirs. The review of past studies shows that the COD of triangular, rectangular and parabolic weirs has not been modeled simultaneously by machine learning algorithms so far. In this research, for the first time, the COD of triangular, rectangular and parabolic weirs is simulated using the weighted robust extreme learning machine (WRELM). Four WRELM models are developed by using the parameters affecting the COD.

Methodology

Extreme Learning Machine (ELM) (Huang et al. 2006) is a new and strong training technique with special characteristics, whose efficiency is well known in solving complex problems in various sciences, including water science and engineering. ELM is a feed-forward neural network training algorithm that has only one layer. One of the most important advantages of this method compared to classical algorithms such as gradient algorithms is the very high speed of this method in the modeling process (Bonakdari et al. 2020). Briefly, the modeling process in this method starts with the random determination of two matrices including the bias of hidden neurons (BHN) and input weights (IW), and continues by using the determined matrices, activation function, and defined data as training data, the output weight matrix is acquired through a linear process. In addition to the high speed of training, other advantages of this method include the ability to approximate unknown functions, very high flexibility, and the existence of only one user-adjustable parameter (i.e., hidden layer neurons). According to the stated advantages, the use of this method is of interest to many researchers in various sciences such as lake water-level fluctuations (Bonakdari et al. 2019); scour depth (Ebtehaj et al. 2019); and rainfall (Zetnoddin et al. 2018). In addition to the stated advantages, this technique also has disadvantages including the use of empirical risk to calculate the output weight, weak control capacity due to the random determination of neurons of the two matrices (i.e., BHN and IW), as well as weak efficiency in the presence of outliers. Therefore, the use of methods such as regularized ELM (RELM) and weighted RELM (WRELM) that solve these problems can be used as an efficient method in solving the problem, along with the advantages of this method. The topics of formulation of classical ELM methods as well as developed ones (i.e., RELM and WRELM) are described below.

The mathematical formula for creating a map** between problem inputs and the desired output in the ELM method is expressed as follows:

$$ \sum\limits_{i = 1}^{q} {\eta_{i} f({{\varvec{\upomega}}}_{i} \cdot {\mathbf{x}}_{j} + B_{i} )} = y_{j} ,\,\,\,\,\,\,\,\,\,\,\,\,\,j = 1,2,..,N $$
(1)

where q denotes the hidden layer neurons number (HLNN), f(x) is the activation function (AF), ω represents the matrix of the output weight, x denotes input variables of the problem, B is the vector of biases related to hidden neurons, y represents the output variable and N is the number of data considered for model training. If the above relations is described in the form of a matrix, so we have:

$$ {\mathbf{K}}\eta = {\mathbf{y}} $$
(2)

where

$$ {\mathbf{K}}({{\varvec{\upomega}}}_{1} ,...,{{\varvec{\upomega}}}_{q} ,{\mathbf{x}}_{1} ,...,{\mathbf{x}}_{N} ,B_{1} ,...,B_{q} ,) = \left[ {\begin{array}{*{20}c} {f{(}{{\varvec{\upomega}}}_{1} \cdot {\mathbf{x}}_{1} + B_{1} )} & \cdots & {f{(}{{\varvec{\upomega}}}_{q} \cdot {\mathbf{x}}_{1} + B_{q} )} \\ \vdots & \ddots & \vdots \\ {f{(}{{\varvec{\upomega}}}_{1} \cdot {\mathbf{x}}_{N} + B_{1} )} & \cdots & {f{(}{{\varvec{\upomega}}}_{q} \cdot {\mathbf{x}}_{N} + B_{q} )} \\ \end{array} } \right]_{N \times q} $$
(3)
$$ \eta = [\eta_{1} ,...,\eta_{q} ]^{T} $$
(4)
$$ {\mathbf{y}} = [y_{1} ,...,y_{N} ]^{T} $$
(5)

The structure of two matrices (i.e., BHN and IW) is initialized completely randomly by having only the HLNN and the number of problem inputs. Therefore, the only unknown value in Eq. 2 is the matrix ω. Considering that the number of problem inputs and the number of defined neurons are not the same, the matrix K is basically a non-square matrix. In order to compute Eq. 2 to obtain ω, the least squares solution of the following loss function is used:

$$ LS_{ELM} = \min \left\| {{\mathbf{y - K}}\omega } \right\| $$
(6)

The optimal value of the above relationship, considering the minimum ℓ2-norm and defining K + as the generalized inverse of K (Rao and Mitra 1971), is as follows:

$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega } = {\mathbf{K}}^{ + } {\mathbf{y}} $$
(7)

Considering that the HLNN is less than the number of samples considered for the model training, the simplified form of the aforementioned relationship is as follows:

$$ \hat{\omega } = ({\mathbf{K}}^{T} {\mathbf{K}})^{ - 1} {\mathbf{K}}^{T} {\mathbf{y}} $$
(8)

According to the results obtained by Bartlett (1997), the highest generalizability in feed-forward-based neural networks is obtained by simultaneously considering the training error and the norm of weights. Therefore, the loss function presented in the ELM method (relation 6) is defined as relation 9.

$$ LF_{RELM} = \mathop {\min }\limits_{\omega } Z\left\| {{\mathbf{y - K}}\eta } \right\|_{2}^{2} + \left\| \eta \right\|_{2}^{2} $$
(9)

To calculate η in the above relation, the Lagrangian multiplier is used. The calculation of η from the above relationship is as follows. Details on the calculation of this parameter are provided in Zhang and Luo (2015).

$$ \hat{\eta } = \left( {{\mathbf{K}}^{T} {\mathbf{K}} + \frac{{\mathbf{I}}}{Z}} \right)^{ - 1} {\mathbf{K}}^{T} {\mathbf{y}} $$
(10)

where I is the unit matrix.

The weighted RELM method (WRELM) is a modified version of the RELM, so that the modeling process in this technique includes three general steps. In the first step, modeling begins using the RELM to provide an initial model. In the second step, the weighting of the error obtained in the previous step begins, so that samples with high errors are given less weight than other samples. Finally, in the third step, using the weightings provided in the second step and reusing the RELM, the final solution related to the WRELM method is provided.

The main idea of develo** the WRELM method compared to the RELM is to use weights and give them an effect on samples used to train the model. In order to provide an efficient model that performs well in the presence of outliers, the RELM error is considered as a variable ei and the weighting factor wi is applied to it. In fact, the term \({\mathbf{e = y - K}}\eta\) in the RELM is considered as. The standard deviation of RELM errors \((\hat{s})\) is defined as follows:

$$ \hat{s} = \frac{{{\text{IQR}}}}{2 \times 0.6745} $$
(11)

In this relation, IQR is equal to the difference between the first and third quartiles of errors. Using the above relationship, the following relationship is defined to apply the weights:

$$ w_{i} = \left\{ {\begin{array}{*{20}c} 1 & {\left| {\frac{{e_{i} }}{{\hat{s}}}} \right| \le 2.5} \\ {\frac{{3 - \left| {\frac{{e_{i} }}{{\hat{s}}}} \right|}}{3 - 2.5}} & {2.5 \le \left| {\frac{{e_{i} }}{{\hat{s}}}} \right| \le 3} \\ {10^{ - 4} } & {{\text{Otherwise}}} \\ \end{array} } \right. $$
(12)

After calculating the weight of each error (above relation), the loss function related to the WRELM is defined as follows:

$$ LS_{{{\text{WRELM}}}} = \mathop {\min }\limits_{\eta } Z\left\| {{\mathbf{We}}} \right\|_{2}^{2} + \left\| \eta \right\|_{2}^{2} \,\,\,\,\,\,\,\,{subjected}\,{to}\,{\mathbf{y - H}}\beta = {\mathbf{e}} $$
(13)

The solution of the above relationship is as follows (Zhang and Luo 2015):

$$ \hat{\eta } = \left( {{\mathbf{K}}^{T} {\mathbf{W}}^{{\mathbf{2}}} {\mathbf{K}} + \frac{{\mathbf{I}}}{Z}} \right)^{ - 1} {\mathbf{K}}^{T} {\mathbf{W}}^{{\mathbf{2}}} {\mathbf{y}} $$
(14)

COD of weirs

Vatankhah and Khamisabadi (2019) displayed the parameters influencing the COD of weirs as a function of discharge (Q), spillway height H, height of the spillway crest (P), flow width (T), channel width (B), flow depth above the spillway crest (h), exponential function (n), gravitational acceleration (g), water surface tension (σ), flow viscosity (μ), and flow density (ρ), as follows:

$$ F\left( {Q,H,P,T,B,h,n,g,\sigma ,\mu ,\rho } \right) = 0 $$
(15)

The following dimensionless groups are defined as the parameters influencing the COD as follows:

$$ \mathop C\nolimits_{d} = \mathop f\nolimits_{1} \left( {\frac{h}{P},\frac{T}{B},\alpha = \frac{{T\mathop h\nolimits^{n} }}{{h\mathop H\nolimits^{n} }},R = \frac{{\rho \sqrt {gh} L}}{\mu },W = \frac{\sigma }{{\rho g\mathop h\nolimits^{2} }}} \right) $$
(16)

Through measurements of laboratory values, the Reynolds number \(\left( {R = \frac{{\rho \sqrt {gh} L}}{\mu }} \right)\) and Weber number \(\left( {W = \frac{\sigma }{{\rho g\mathop h\nolimits^{2} }}} \right)\) are considered constant. So, the above relationship is rewritten as:

$$ \mathop C\nolimits_{d} = \mathop f\nolimits_{2} \left( {\frac{h}{P},\frac{T}{B},\alpha = \frac{{T\mathop h\nolimits^{n} }}{{h\mathop H\nolimits^{n} }}} \right) $$
(17)

So, the variables shown in the above formula are considered as WRELM model inputs. The combinations of the input parameters for the extension of the WRELMs are depicted in Fig. 1.

Fig. 1
figure 1

Combinations of input variables for develo** WRELM models

Full size image

Experimental apparatus

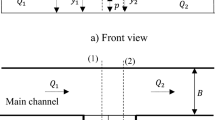
In this paper, the laboratory values reported by Vatankhah and Khamisabadi (2019) are utilized to validate the RELM models. The applied experimental study was recently published (2019), and it is quite comprehensive; hence, this study has been used in the current investigation. In their experimental model, the flow rates were measured under free surface conditions. The laboratory model consisted of a horizontal rectangular channel with a length of 12 m, a width of 25 cm and a depth of 50 cm. The side walls of the rectangular channel were made of transparent glass. The canal was attached to the upstream source via a stilling tank to remove water level fluctuations. The weirs were installed 6 m downstream of the channel inlet to ensure that the spillway flow is independent of the inlet flow fluctuations. From a large tank with a fixed head, water was supplied by a recharge pipe equipped with a control valve to the inlet of the canal. From the downstream end of the main channel, the water passed through a triangular spillway and entered a groundwater tank and then, circulated to the fixed head tank using a pump. The number of experimental cases was 502. Figure 2 depicts the laboratory model used by Vatankhah and Khamisabadi (2019).

Fig. 2
figure 2

Experimental model used by vatankhah and Khamisabadi (2019)

Full size image

Goodness of fit

To evaluate the efficiency of the introduced RELM models, the following statistical indices are employed (Azimi and Shiri 2020):

Correlation coefficient (R).

Variance accounted for (VAF).

Root mean square error (RMSE).

Scatter index (SI).

Mean absolute error (MAE).

Nash Sutcliffe efficiency coefficient (NSC)

$$ R = \frac{{\sum\nolimits_{i = 1}^{n} {\left( {F_{i} - \overline{F} } \right)\left( {O_{i} - \overline{O} } \right)} }}{{\sqrt {\sum\nolimits_{i = 1}^{n} {\left( {F_{i} - \overline{F} } \right)^{2} \sum\nolimits_{i = 1}^{n} {\left( {O_{i} - \overline{O} } \right)^{2} } } } }} $$
(18)
$$ \text{VAF} = \left( {{1} - \frac{{{var}\left( {F_{i} - O_{i} } \right)}}{{{var}\left( {F_{i} } \right)}}} \right) \times {100} $$
(19)
$$ {\text{RMSE}} = \sqrt {\frac{1}{n}\sum\nolimits_{i = 1}^{n} {\left( {F_{i} - O_{i} } \right)^{2} } } $$
(20)
$$ {\text{NRMSE}} = \frac{{{\text{RMSE}}}}{{\overline{O} }} $$
(21)
$$ {\text{MAE}} = \frac{1}{n}\sum\limits_{i = 1}^{n} {\left| {F_{i} - O_{i} } \right|} $$
(22)
$$ {\text{NSC}} = 1 - \frac{{\sum\limits_{i = 1}^{n} {\left( {O_{i} - F_{i} } \right)^{2} } }}{{\sum\limits_{i = 1}^{n} {\left( {O_{i} - \overline{O} } \right)^{2} } }} $$
(23)

here, Oi represents values of the laboratory COD, Fi denotes modeled values, \(\overline{O}\) is the average of observed values and equal to the number of observed values. In the following sections, the efficiency of the RELM models in simulating the COD is discussed. In this study, the laboratory data are used to train and test the RELM learning machines. The mentioned data are divided into two categories including training (70% of all data) and test (remaining 30%). The significant findings of the current research are provided in the next sections.

Results and discussion

At the beginning, the optimal HLNN and the superior AF are chosen. After that, by executing a series of analyses, the superior WRELM and the superior input variables are introduced. Next, the superior WRELM is compared with the ELM. Eventually, a relationship is proposed to estimate COD values. To choose the optimal number of NHN, best activation function, and the best value for the C parameter, the WRELM 1 was considered as the benchmark model.

Number of hidden neurons

In the first step, the effect of the HLNN on the WRELM efficiency is examined. In general, finding the optimal HLNN significantly affects the performance of machine learning algorithms (Azimi et al. 2021). Firstly, in the present study, a neuron is embedded in the hidden layer and then, the WRELM efficiency is investigated. Then, the number of these neurons is increased to fifteen. The results of various statistical indices calculated versus the changing pattern of the HLNN are shown in Fig. 3. As it can be seen, the WRELM does not show good accuracy at first, but with the increase in the HLNN, the performance of this algorithm to estimate the values of the COD improves significantly. For example, when the HLNN = 1, the RMSE and MAE statistical indices are calculated to be 0.041 and 0.031, separately. Additionally, the values of R and VAF for the situation where four neurons are inside the hidden layer are equal to 0.836 and 67.182, separately. The analysis of the obtained results indicates that the WRELM with HLNN = 9 has an acceptable performance.

Fig. 3
figure 3

Results of various statistical indices calculated versus the trend of changes in the number of hidden layer neurons

Full size image

Figure 4 also compares the CODs simulated by the WRELM with HLNN = 9 with the experimental values. For these conditions, the RMSE, MAE and R values are obtained to be 0.001, 0.0007 and 0.976, individually. The WRELM algorithm with HLNN = 9 shows an acceptable performance, so in the following, the same number of neurons in the hidden layer is used to simulate the COD values of triangular, rectangular and parabolic weirs.

Fig. 4
figure 4

COD simulated by WRELM for the case where HLNN = 9 with experimental values

Full size image

Activation function (AF)

In this part, the impact of different AFs on the performance of the WRELM algorithm in estimating the COD of triangular, rectangular and parabolic weirs is discussed. In general, choosing the proper activation function for the machine learning algorithm has an important effect on the simulation results (Azimi and Shiri 2021b). In this study, six different AFs comprising tangent hyperbolic (Tanh), triangular basis (tribas), radial basis (radbas), hardlimit (Hardlim), sigmoid (sig) and sinusoidal (sin) are used to predict the COD values. Triangular, rectangular and parabolic shapes were used. The results of the statistical indices computed for different AFs can be seen in Fig. 5. According to the simulation outcomes, the tribas function displays the worst performance. For tribas, the R and NSC values are acquired to be 0.691 and 0.462, separately. In addition, for the sin, Tanh and hardlim, the RMSE values are equal to 0.0018, 0.002 and 0.0023, respectively. Meanwhile, for the radbas function, the MAE and NRMSE values are estimated equal to 0.001 and 0.002, separately.

Fig. 5
figure 5

The results of statistical indices calculated for different activation functions

Full size image

The comparison between the efficiency of different activation functions shows that the sig function recreates the COD values more accurately. For the sig activation function, the NSC, NRMSE and R values are equal to 0.950, 0.002 and 0.976, separately. Figure 6 shows the scatter plot along with the comparison between the experimental CODs and CODs simulated by the WRELM algorithm with the sig activation function. As can be seen, the sig activation function displays a good performance for simulating COD values, so the sig activation function is used for the WRELM algorithm.

Fig. 6
figure 6

Scatter plot along with comparison between laboratory CODs and CODs simulated by WRELM algorithm with sig activation function

Full size image

Regularization parameter(C)

The regularization parameter (C) of the WRELM algorithm is evaluated in this section. In the first step, the value of the parameter C is assumed equal to 0.001 and the value of this parameter is reduced in each step and the values of 0.0004, 0.0002, 0.0001, 0.00005 and 0.000025 are defined for the regularization parameter. Figure 7 shows the results of various statistical indices calculated for various values of the regularization parameter. According to the modeling results, the worst performance of the WRELM algorithm is obtained for the regularization parameter equal to 0.001. Moreover, the NRMSE and VAF for C = 0.001 are equal to 0.003 and 90.064. For the situation where the regularization parameter is equal to 0.000025, the values of MAE, R and NSC are acquired to be 0.0007, 0.967 and 0.917, separately.

Fig. 7
figure 7

The results of different statistical indices calculated for different values of the regularization parameter

Full size image

The analysis of the modeling findings demonstrates that the WRELM algorithm with the regularization parameter equal to 0.0001 has better efficiency. For C = 0.0001, the RMSE, VAF and NSC are acquired to be 0.001, 95.163 and 0.950, separately. Figure 8 also shows the comparison of the laboratory CODs with the values simulated by the WRELM algorithm with C = 0.0001 along with their scatter diagram. Therefore, in order to simulate the COD values, the regularization parameter equal to 0.0001 is used.

Fig. 8
figure 8

Comparison of the laboratory CODs with values simulated by the WRELM algorithm with C = 0.0001 along with the scatter plot

Full size image

WRELM models

Using the input variables, four WRELM models are extended. In this part, the performance of the WRELM models is evaluated. In Fig. 9, the outcomes of the statistical indices computed for the WRELMs are arranged. WRELM 1 reproduces the COD amounts using \({h \mathord{\left/ {\vphantom {h P}} \right. \kern-0pt} P},{T \mathord{\left/ {\vphantom {T B}} \right. \kern-0pt} B},\alpha = {{Th^{n} } \mathord{\left/ {\vphantom {{Th^{n} } {hH^{n} }}} \right. \kern-0pt} {hH^{n} }}\). For WRELM 1, the RMSE, MAE and VAF values are estimated to be 0.001, 0.0007 and 95.163, respectively. The simulation results display that the WRELM 1 model is the third best model. The dimensionless parameters are used to estimate the COD using the WRELM 2 model, and the influence of the parameter is eliminated. The R and NRMSE statistical indices for WRELM 2 are also equal to 0.750 and 0.006, individually. WRELM 2 is identified as the weakest model in predicting the COD. The analysis of the simulation displays showed that WRELM 3 is the second-best model for simulating the COD of triangular, rectangular and parabolic weirs. For WRELM 3, the values of NSC and VAF are acquired to be 0.963 and 96.448, separately. It is worth mentioning that WRELM 3 is a function of \({h \mathord{\left/ {\vphantom {h P}} \right. \kern-0pt} P},\alpha\). Moreover, for WRELM 4, the MAE and R values are acquired to be 0.0004 and 0.993, respectively. It should be pointed out that the WRELM 4 model is the best model in terms of performance, which models the COD values in terms of \({T \mathord{\left/ {\vphantom {T B}} \right. \kern-0pt} B},\alpha\).

Fig. 9
figure 9

Results of statistical indices calculated for WRELMs

Full size image

The analysis of the obtained results indicates that the dimensionless parameters α and T/B are the most effective input parameters for estimating the COD of triangular, rectangular and parabolic weirs.

The simulation results demonstrate that WRELM 4 which predicts the values of the COD of triangular, rectangular and parabolic weirs using \({T \mathord{\left/ {\vphantom {T B}} \right. \kern-0pt} B},\alpha\) is introduced as the best model in this study. The comparison of the CODs simulated by WRELM 4 model with the laboratory amounts along with their scatter plots is depicted in Fig. 10. The WRELM 4 model estimates the COD values with the minimum error and the maximum correlation.

Fig. 10
figure 10

Comparison of CODs recreated by WRELM 4 model with laboratory values along with scatter plots

Full size image

Comparison with ELM

Next, the performance of the superior WRELM model is compared with the ELM algorithm. The outcomes of the calculated statistical indices for the WRELM and ELM models can be seen in Fig. 11. This comparison demonstrates the better efficiency of the WRELM algorithm for simulating the COD of triangular, rectangular and parabolic weirs. For example, the values of the R index for WRELM and ELM are equal to 0.994 and 0.971, separately. In addition, for the WRELM and ELM, the MAE values are calculated to be 0.0004 and 0.0008, respectively.

Fig. 11
figure 11

Results of the statistical indices calculated for the WRELM and ELM models

Full size image

Figure 12 also shows the comparison between the CODs acquired by the WRELM and ELM models along with their scatter plots. This comparison indicates the better performance of the WRELM algorithm to estimate the COD values of triangular, rectangular and parabolic weirs, so that the WRELM model has higher correlation and more accuracy.

Fig. 12
figure 12

Comparison between CODs simulated by WRELM and ELM models along with scatter plots

Full size image

Superior WRELM model

In this section, WRELM 4 is introduced as the superior model. It should be remembered that WRELM 4 simulates the COD values in terms of \({T \mathord{\left/ {\vphantom {T B}} \right. \kern-0pt} B},\alpha = {{Th^{n} } \mathord{\left/ {\vphantom {{Th^{n} } {hH^{n} }}} \right. \kern-0pt} {hH^{n} }}\). It should be noted that the general form of the equation derived from the WRELM method is as follows:

$$ C_{d} = \left[ {\frac{1}{{\left( {1 + \exp \left( {{\text{In}}W \times {\text{In}}V + {\text{BHN}}} \right)} \right)}}} \right]^{T} \times {\text{Out}}W $$
(24)

where, InW, InV, BHN and OutW are the matrices of input weights, input variables, bias of hidden neurons and output weights, respectively.

The matrices of WRELM4 are presented as:

$$ InV{ = }\left[ {\begin{array}{*{20}c} {{T \mathord{\left/ {\vphantom {T B}} \right. \kern-0pt} B}} \\ \alpha \\ \end{array} } \right] $$
(25)
$$ {\text{BHN}} = \left[ {\begin{array}{*{20}c} {{ - 0}{\text{.397}}} \\ {{0}{\text{.273}}} \\ {{ - 0}{\text{.152}}} \\ {{ - 0}{\text{.230}}} \\ {{0}{\text{.524}}} \\ {{ - 0}{\text{.236}}} \\ {{0}{\text{.554}}} \\ {{ - 0}{\text{.039}}} \\ {{ - 0}{\text{.223}}} \\ \end{array} } \right]\,\,\,{\text{In}}W = \left[ {\begin{array}{*{20}c} {{ - 0}{\text{.170}}} & {{0}{\text{.424}}} \\ {{0}{\text{.520}}} & {{ - 0}{\text{.161}}} \\ {{0}{\text{.283}}} & {{ - 0}{\text{.226}}} \\ {{0}{\text{.021}}} & {{ - 0}{\text{.387}}} \\ {{0}{\text{.417}}} & {{0}{\text{.102}}} \\ {{ - 0}{\text{.466}}} & {{0}{\text{.174}}} \\ {{ - 0}{\text{.115}}} & {{0}{\text{.022}}} \\ {{0}{\text{.332}}} & {{0}{\text{.110}}} \\ {{ - 0}{\text{.318}}} & {{ - 0}{\text{.734}}} \\ \end{array} } \right]\,\,\,{\text{Out}}W = \left[ {\begin{array}{*{20}c} {{29}{\text{.764}}} \\ {{ - 142}{\text{.536}}} \\ {{ - 30}{\text{.428}}} \\ {{52}{\text{.093}}} \\ {{ - 27}{\text{.617}}} \\ {{ - 214}{\text{.217}}} \\ {{231}{\text{.887}}} \\ {{58}{\text{.871}}} \\ {{ - 8}{\text{.188}}} \\ \end{array} } \right] $$

Partial derivative sensitivity analysis (PDSA)

In this section, a partial derivative sensitivity analysis (PDSA) is performed for the WRELM 4 model as the most efficient model. Basically, the PDSA is executed to identify the effect of input parameters on the COD. In other words, the PDSA is one of the techniques to identify the pattern of target parameter changes on the basis of to the input variables. A positive PDSA means an increase in the COD, and a negative PDSA means a decrease in its value. Moreover, in this technique, the relative derivative of each input variable is acquired regarding the target function (Azimi et al. 2022). The PDSA outcomes for WRELM 4 are depicted in Fig. 13. WRELM 4 acquires the CODs using the parameters \({T \mathord{\left/ {\vphantom {T B}} \right. \kern-0pt} B},\alpha\). For the parameter \({T \mathord{\left/ {\vphantom {T B}} \right. \kern-0pt} B}\), part of the PDSA results is computed as positive and the other part as negative. This is despite the fact that with increasing the α values, the PDSA results increase, and part of these results are computed as positive and the other part as negative.

Fig. 13
figure 13

PDSA results for WRELM 4 model

Full size image

Conclusion

In the present study, the COD of triangular, rectangular and parabolic weirs was simulated via the weighted robust extreme learning machine (WRELM) algorithm. Four distinct WRELM learning machine models were developed using the COD effective variables.

  • To validate these WRELM models, a dataset was used, in which approximately 70% of these data were utilized to train the WRELMs and the rest 30% were used to test them.

  • By implementing a trial-and-error procedure, nine neurons were embedded in the hidden layer and the sigmoid function was chosen as the best AF of the algorithm.

  • It should be noted that the optimal regularization parameter for the WRELM algorithm was equal to 0.0001.

  • By analyzing the simulation results, the best model and the most effective input parameters were identified.

  • WRELM 4 was chosen as the superior model because this model had the highest exactness and correlation with the laboratory values, so that the NSC and RMSE for it were acquired to be 0.987 and 0.0007, separately.

  • In addition, the dimensionless input parameters α and T/B were the most effective input variables.

  • The comparison of the outcomes of the superior WRELM model with the ELM algorithm showed the remarkable superiority of the model.

  • For practical works, a relationship was proposed to calculate the COD values of triangular, rectangular and parabolic weirs.

  • A PDSA analysis was also performed for the superior model and the proposed relationship.

Presenting an explicit WRELM-based model to estimate the discharge coefficient of weirs with different shapes is the most important benefit of the current study. The discharge coefficient of side weirs can be estimated by other machine learning algorithms and optimization tools.