SpringerLink
Log in

A High Order Numerical Scheme for Time-Fractional Telegraph Equation Via Cubic Spline in Tension

  • Original Research
  • Published:
Differential Equations and Dynamical Systems Aims and scope Submit manuscript

Abstract

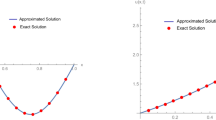
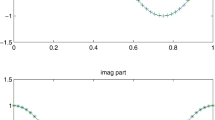
In this work, we examine the numerical solution of the time-fractional telegraph equation by applying a higher-order numerical scheme via the tension spline method. The fractional order derivative of two different orders is analyzed using Caputo’s definition. Moreover, the numerical scheme formation was carried out using spline functions incorporating the tension parameter in the spatial direction and the discretization technique based on a finite difference approach in the temporal direction. The proposed scheme includes some parameters, and by a suitable choice of parameters, its order can be enhanced from two to four in the spatial direction. The present technique is proven unconditionally stable through meticulous analysis. The convergence analysis is also demonstrated using the Fourier series. Numerical results of two test examples are presented through tables and plots that show the proficiency of the proposed numerical scheme and validate our theoretical findings.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
EUR 32.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or Ebook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (United Kingdom)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

Data availability

Data sharing does not apply to this article, as no data sets were generated or analyzed during the current study.

References

  1. Abdou, M.: Adomian decomposition method for solving the telegraph equation in charged particle transport. J. Quant. Spectrosc. Radiat. Transf. 95, 407–414 (2005)

    Article  ADS  CAS  Google Scholar 

  2. Aghamohamadi, M., Rashidinia, J., Ezzati, R.: Tension spline method for solution of non-linear Fisher equation. Appl. Math. Comput. 249, 399–407 (2014)

    MathSciNet  Google Scholar 

  3. Agrawal, O.P.: Solution for a fractional diffusion-wave equation defined in a bounded domain. Nonlinear Dyn. 29, 145–155 (2002)

    Article  MathSciNet  Google Scholar 

  4. Bansu, H., Kumar, S.: Numerical solution of space and time fractional telegraph equation: a meshless approach. Int. J. Nonlinear Sci. Numer. Simul. 20, 325–337 (2019)

    Article  MathSciNet  Google Scholar 

  5. Barletta, A., Zanchini, E.: A thermal potential formulation of hyperbolic heat conduction. J. Heat Transfer 121, 166–169 (1999)

    Article  CAS  Google Scholar 

  6. Biazar, J., Eslami, M.: Analytic solution for telegraph equation by differential transform method. Phys. Lett. A 374, 2904–2906 (2010)

    Article  ADS  MathSciNet  CAS  Google Scholar 

  7. Chawla, R., Deswal, K., Kumar, D., Baleanu, D.: Numerical simulation for generalized time-fractional Burgers’ equation with three distinct linearization schemes. J. Comput. Nonlinear Dyn. 18, 041001 (2023)

    Article  Google Scholar 

  8. Chawla, R., Kumar, D.: Higher-order tension spline-based numerical technique for time fractional reaction-diffusion wave equation with dam**. Int J Dyn Control (2023). https://doi.org/10.1007/s40435-023-01222-5

    Article  Google Scholar 

  9. Chen, J., Liu, F., Anh, V.: Analytical solution for the time-fractional telegraph equation by the method of separating variables. J. Math. Anal. Appl. 338, 1364–1377 (2008)

    Article  MathSciNet  Google Scholar 

  10. Cui, M.: Compact finite difference method for the fractional diffusion equation. J. Comput. Phys. 228, 7792–7804 (2009)

    Article  ADS  MathSciNet  CAS  Google Scholar 

  11. Das, S., Vishal, K., Gupta, P.K., Yildirim, A.: An approximate analytical solution of time-fractional telegraph equation. Appl. Math. Comput. 217, 7405–7411 (2011)

    MathSciNet  Google Scholar 

  12. De Staelen, R.H., Hendy, A.S.: Numerically pricing double barrier options in a time-fractional Black–Scholes model. Comput. Math. Appl. 74, 1166–1175 (2017)

    Article  MathSciNet  Google Scholar 

  13. Dehghan, M., Shokri, A.: A numerical method for solving the hyperbolic telegraph equation. Numer. Methods Partial Differ. Equ. 24, 1080–1093 (2008)

    Article  MathSciNet  Google Scholar 

  14. Delić, A., Jovanović, Bo.ško S., Živanović, S.: Finite difference approximation of a generalized time-fractional telegraph equation. Comput. Appl. Math. 20, 595–607 (2020)

    MathSciNet  Google Scholar 

  15. Esmaeili, S., Shamsi, M.: A pseudo-spectral scheme for the approximate solution of a family of fractional differential equations. Commun. Nonlinear Sci. Numer. Simul. 16, 3646–3654 (2011)

    Article  ADS  MathSciNet  Google Scholar 

  16. Ford, N.J., Rodrigues, M.M., **ao, J., Yan, Y.: Numerical analysis of a two-parameter fractional telegraph equation. J. Comput. Appl. Math. 249, 95–106 (2013)

    Article  MathSciNet  Google Scholar 

  17. Gregory, J.A., Sarfraz, M.: A rational cubic spline with tension. Comput. Aided Geom. Des. 7, 1–13 (1990)

    Article  MathSciNet  Google Scholar 

  18. Hashemi, M.S., Baleanu, D.: Numerical approximation of higher-order time-fractional telegraph equation by using a combination of a geometric approach and method of line. J. Comput. Phys. 316, 10–20 (2016)

    Article  ADS  MathSciNet  Google Scholar 

  19. Hesameddini, E., Asadolahifard, E.: A new spectral Galerkin method for solving the two dimensional hyperbolic telegraph equation. Comput. Math. Appl. 72, 1926–1942 (2016)

    Article  MathSciNet  Google Scholar 

  20. Heydari, M.H., Hooshmandasl, M.R., Mohammadi, F.: Two-dimensional Legendre wavelets for solving time-fractional telegraph equation. Adv. Appl. Math. Mech. 6, 247–260 (2014)

    Article  MathSciNet  Google Scholar 

  21. Hilfer, R.: Applications of Fractional Calculus in Physics. World Scientific, Singapore (2000)

    Book  Google Scholar 

  22. Hosseini, V.R., Chen, W., Avazzadeh, Z.: Numerical solution of fractional telegraph equation by using radial basis functions. Eng. Anal. Bound. Elem. 38, 31–39 (2014)

    Article  MathSciNet  Google Scholar 

  23. Jordan, P.M., Puri, A.: Digital signal propagation in dispersive media. J. Appl. Phys. 85, 1273–1282 (1999)

    Article  ADS  CAS  Google Scholar 

  24. Kanth, A.S.V., Sirswal, D.: Analysis and numerical simulation for a class of time fractional diffusion equation via tension spline. Numer. Algorithms 79, 479–497 (2018)

    Article  MathSciNet  Google Scholar 

  25. Khan, I., Aziz, T.: Tension spline method for second-order singularly perturbed boundary-value problems. Int. J. Comput. Math. 82, 1547–1553 (2005)

    Article  MathSciNet  Google Scholar 

  26. Khan, Y., Diblik, J., Faraz, N., Smarda, Z.: An efficient new perturbative Laplace method for space-time fractional telegraph equations. Adv. Differ. Equ. 2012, 204 (2012). https://doi.org/10.1186/1687-1847-2012-204

    Article  MathSciNet  Google Scholar 

  27. Kilbas, A.A., Srivastava, H.M., Trujillo, J.J.: Theory and Applications of Fractional Differential Equations. North-Holland, New York (2006)

    Google Scholar 

  28. Lakestani, M., Saray, B.N.: Numerical solution of telegraph equation using interpolating scaling functions. Comput. Math. Appl. 60, 1964–1972 (2010)

    Article  MathSciNet  Google Scholar 

  29. Lin, Y., Xu, C.: Finite difference/spectral approximations for the time-fractional diffusion equation. J. Comput. Phys. 225, 1533–1552 (2007)

    Article  ADS  MathSciNet  Google Scholar 

  30. Miller, K.S., Ross, B.: An Introduction to the Fractional Calculus and Fractional Differential Equations. Wiley, New York (1993)

    Google Scholar 

  31. Momani, S., Odibat, Z., Alawneh, A.: Variational iteration method for solving the space- and time-fractional KdV equation. Numer. Methods Partial Differ. Equ. 24, 262–271 (2008)

    Article  MathSciNet  Google Scholar 

  32. Orsingher, E., Beghin, L.: Time-fractional telegraph equations and telegraph processes with Brownian time. Probab. Theory Relat. Fields 128, 141–160 (2004)

    Article  MathSciNet  Google Scholar 

  33. Perdikaris, P., Karniadakis, G.E.: Fractional-order viscoelasticity in one-dimensional blood flow models. Ann. Biomed. Eng. 42, 1012–1023 (2014)

    Article  PubMed  Google Scholar 

  34. Podlubny, I.: Fractional Differential Equations. Academic Press, San Diego (1999)

    Google Scholar 

  35. Saadatmandi, A., Dehghan, M.: Numerical solution of hyperbolic telegraph equation using the Chebyshev tau method. Numer. Methods Partial Differ. Equ. 26, 239–252 (2010)

    Article  MathSciNet  Google Scholar 

  36. Saadatmandi, A., Dehghan, M.: A Tau approach for solution of the space fractional diffusion equation. Comput. Math. Appl. 62, 1135–1142 (2011)

    Article  MathSciNet  Google Scholar 

  37. Schumer, R., Benson, D.A., Meerschaert, M.M., Baeumer, B.: Fractal mobile/immobile solute transport. Water Resour. Res. 39(10), 1296 (2003). https://doi.org/10.1029/2003WR002141

    Article  ADS  Google Scholar 

  38. Sharifi, S., Rashidinia, J.: Numerical solution of hyperbolic telegraph equation by cubic B-spline collocation method. Appl. Math. Comput. 281, 28–38 (2016)

    MathSciNet  Google Scholar 

  39. Shekarabi, H.S., Rashidinia, J.: Three level implicit tension spline scheme for solution of convection-reaction-diffusion equation. Ain Shams Eng. J. 9, 1601–1610 (2018)

    Article  Google Scholar 

  40. Wei, L., Liu, L., Sun, H.: Numerical methods for solving the time-fractional telegraph equation. Taiwan. J. Math. 22, 1509–1528 (2018)

    Article  MathSciNet  Google Scholar 

  41. Weston, V., He, S.: Wave splitting of the telegraph equation in \(R^3\) and its application to inverse scattering. Inverse Probl. 9, 789 (1993)

    Article  ADS  MathSciNet  Google Scholar 

  42. Yousefi, S.A., Lotfi, A., Dehghan, M.: The use of a Legendre multiwavelet collocation method for solving the fractional optimal control problems. J. Vib. Control 17, 2059–2065 (2011)

    Article  MathSciNet  Google Scholar 

  43. Zhang, Y., Qian, J., Papelis, C., Sun, P., Yu, Z.: Improved understanding of bimolecular reactions in deceptively simple homogeneous media: from laboratory experiments to Lagrangian quantification. Water Resour. Res. 50, 1704–1715 (2014)

    Article  ADS  Google Scholar 

Download references

Acknowledgements

The authors sincerely thank the reviewers for providing valuable comments to improve the manuscript.

Funding

No funding was received.

Author information

Authors and Affiliations

  1. Department of Mathematics, Birla Institute of Technology and Science, Pilani, Rajasthan, 333031, India

    Reetika Chawla & Devendra Kumar

Authors
  1. Reetika Chawla
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Devendra Kumar
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Reetika Chawla.

Ethics declarations

Conflict of interest

The authors state that they have no known competing financial interests or personal ties that could have influenced the research presented in this study.

Ethical approval

Not applicable.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chawla, R., Kumar, D. A High Order Numerical Scheme for Time-Fractional Telegraph Equation Via Cubic Spline in Tension. Differ Equ Dyn Syst (2024). https://doi.org/10.1007/s12591-024-00678-x

Download citation

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s12591-024-00678-x

Keywords

Mathematics Subject Classification

Search

Navigation