SpringerLink
Log in

The effect of Kelvin–Voigt dam** on the stability of Timoshenko laminated beams system with history

  • Published:
Rendiconti del Circolo Matematico di Palermo Series 2 Aims and scope Submit manuscript

Abstract

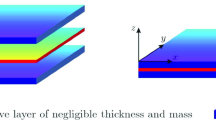
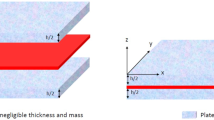
This paper considers a model composed of two identical and uniform Timoshenko beams, one on top of the other, which are held together by an adhesive layer of negligible thickness, allowing interfacial slip between them. Using a semigroup approach and the frequency domain method, we study the system’s global well-posedness and asymptotic behavior under the influence of Kelvin–Voigt and memory-type dam**s. It is well-known that if the wave propagation speeds are equal, a single memory dam** on the rotation equation can exponentially drive the system to equilibrium. In this work, we study the impact of introducing Kelvin–Voigt dam** on the displacement equation. We prove that the presence of Kelvin–Voigt dam** destroys the exponential stability of the system achieved with memory dam**. In light of the lack of exponential stability, we show that the system is polynomially stable.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
EUR 32.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or Ebook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Germany)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Similar content being viewed by others

References

  1. Alves, M.S., Monteiro, R.N.: Exponential stability of laminated Timoshenko beams with boundary/internal controls. J. Math. Anal. Appl. (2020). https://doi.org/10.1016/j.jmaa.2019.123516Corpus

    Article  MathSciNet  Google Scholar 

  2. Ammar-Khodja, F., Benabdallah, A., Muñoz Rivera, J.E., Racke, R.: Energy decay for Timoshenko systems of memory type. J. Differ. Equ. 194(1), 82–115 (2003). https://doi.org/10.1016/S0022-0396(03)00185-2

    Article  MathSciNet  Google Scholar 

  3. Boltzmann, L.: Zur Theorie der elastischen Nachwirkung. Wien. Ber. 70, 275–306 (1874)

    Google Scholar 

  4. Boltzmann, L.: Zur Theorie der elastischen Nachwirkung. Wied. Ann. 5, 430–432 (1878)

    Article  Google Scholar 

  5. Borichev, A., Tomilov, Y.: Optimal polynomial decay of functions and operator semigroups. Math. Ann. 347, 455–478 (2010). https://doi.org/10.1007/s00208-009-0439-0

    Article  MathSciNet  Google Scholar 

  6. Brezis, H.: Functional Analysis, Sobolev Spaces and Partial Differential Equations. Universitext Springer, New York (2011). https://doi.org/10.1007/978-0-387-70914-7

    Book  Google Scholar 

  7. Cabanillas, V.R., Quispe, T., Sánchez, J.: Optimal polynomial stability for laminated beams with Kelvin–Voigt dam**. Math. Methods Appl. Sci. 45(16), 9578 (2022)

    Article  MathSciNet  Google Scholar 

  8. Cabanillas, V.R., Raposo, C.A.: Exponential stability for laminated beams with intermediate dam**. Arch. Math. 118, 625–635 (2022). https://doi.org/10.1007/s00013-022-01730-4

    Article  MathSciNet  Google Scholar 

  9. Campbell, F.C.: Manufacturing Processes for Advanced Composites. Elsevier Advanced Technology, Oxford (2004). https://doi.org/10.1016/b978-185617415-2/50002-2

    Book  Google Scholar 

  10. Dafermos, C.M.: Asymptotic stability in viscoelasticity. Arch. Ration. Mech. Anal. 37, 297–308 (1970)

    Article  MathSciNet  Google Scholar 

  11. Elishakoff, I.: Who developed the so-called Timoshenko beam theory? Math. Mech. Solids (2019). https://doi.org/10.1177/1081286519856931

    Article  Google Scholar 

  12. Fabrizio, M., Giorgi, C., Pata, V.: A new approach to equations with memory. Arch. Ration. Mech. Anal. 198, 189–232 (2010). https://doi.org/10.1007/s00205-010-0300-3

    Article  MathSciNet  Google Scholar 

  13. Fatori, L., Muñoz Rivera, J.: Rates of decay to weak thermoelastic Bresse system. IMA J. Appl. Math. 75(6), 881–904 (2010). https://doi.org/10.1093/imamat/hxq038

    Article  MathSciNet  Google Scholar 

  14. Feng, B., Almeida Júnior, D.S., Ramos, A.J.A.: Exponential stabilization of laminated beams with history memories. Math. Nachr. 294, 559–579 (2021). https://doi.org/10.1002/mana.202000337

    Article  MathSciNet  Google Scholar 

  15. Gearhart, L.M.: Spectral theory for contraction semigroups on Hilbert spaces. Trans. Am. Math. Soc. 236, 385–394 (1978). https://doi.org/10.1090/S0002-9947-1978-0461206-1

    Article  MathSciNet  Google Scholar 

  16. Giorgi, C., Pata, V., Marzocchi, A.: Asymptotic behavior of a semilinear problem in heat conduction with memory. Nonlinear Differ. Equ. Appl. 5(3), 333–354 (1998)

    Article  MathSciNet  Google Scholar 

  17. Guesmia, A., Messaoudi, S.A.: On the stabilization of Timoshenko systems with memory and different speeds of wave propagation. Appl. Math. Comput. 219, 9424–9437 (2013). https://doi.org/10.1016/j.amc.2013.03.105

    Article  MathSciNet  Google Scholar 

  18. Guesmia, A., Messaoudi, S., Soufyane, A.: On the stabilization for a linear Timoshenko system with infinite history and applications to the coupled Timoshenko-heat systems. Electron. J. Differ. Equ. 2012, 1–45 (2012)

    Google Scholar 

  19. Guesmia, A.: Well-posedness and stability results for laminated Timoshenko beams with interfacial slip and infinite memory. IMA J. Math. Control Inf. 37(1), 300–350 (2020). https://doi.org/10.1093/imamci/dnz002

    Article  MathSciNet  Google Scholar 

  20. Hansen, S.W., Spies, R.D.: Structural dam** in laminated beams due to interfacial slip. J. Sound Vib. 204(2), 183–202 (1997). https://doi.org/10.1006/jsvi.1996.0913

    Article  Google Scholar 

  21. Huang, F.: Characteristic conditions for exponential stability of linear dynamical systems in Hilbert spaces. Ann. Differ. Equ. 1, 43–56 (1985)

    MathSciNet  Google Scholar 

  22. Li, G., Kong, X., Liu, W.: General decay for a laminated beam with structural dam** and memory: the case of non-equal wave speeds. J. Integral Equ. Appl. 30(1), 95–116 (2018). https://doi.org/10.1216/JIE-2018-30-1-95

    Article  MathSciNet  Google Scholar 

  23. Liu, Z., Zheng, S.: Semigroup Associated with Dissipative Systems. Res. Notes Math., vol. 398. Chapman & Hall/CRC, Boca Raton (1999)

    Google Scholar 

  24. Liu, W., Zhao, W.: Stabilization of a thermoelastic laminated beam with past history. Appl. Math. Optim. 80, 103–133 (2019). https://doi.org/10.1007/s00245-017-9460-y

    Article  MathSciNet  Google Scholar 

  25. Lo, A., Tatar, N.-E.: Stabilization of laminated beams with interfacial slip. Electron. J. Differ. Equ. 129, 1–14 (2015)

    MathSciNet  Google Scholar 

  26. Lo, A., Tatar, N.E.: Uniform stability of a laminated beam with structural memory. Qual. Theory Dyn. Syst. 15, 517–540 (2016). https://doi.org/10.1007/s12346-015-0147-y

    Article  MathSciNet  Google Scholar 

  27. Lo, A., Tatar, N.E.: Exponential stabilization of a structure with interfacial slip. Discrete Contin. Dyn. Syst. 36, 6285–6306 (2016). https://doi.org/10.3934/dcds.2016073

    Article  MathSciNet  Google Scholar 

  28. Mahajan, Y., Roy, J. (eds.): Handbook of Advanced Ceramics and Composites. Defense, Security, Aerospace and Energy Applications, Springer, Cham (2019)

    Google Scholar 

  29. Mikhasev, G.I., Altenbach, H.: Thin-Walled Laminated Structures: Buckling, Vibrations and Their Suppression. Springer, London (2019). https://doi.org/10.1007/978-3-030-12761-9

    Book  Google Scholar 

  30. Muñoz, J., Racke, R.: Global stability for damped Timoshenko systems. Discrete Cont. Dyn. Syst. 9(6), 1625–1639 (2003)

    Article  MathSciNet  Google Scholar 

  31. Pazy, A.: Semigroups of Linear Operators and Applications to Partial Differential Equations, vol. 44. Springer, New York (2012)

    Google Scholar 

  32. Prüss, J.: On the spectrum of \(C_{0}\)-semigroups. Trans. Am. Math. Soc. 284, 847–857 (1984). https://doi.org/10.1090/S0002-9947-1984-0743749-9

    Article  Google Scholar 

  33. Quispe Méndez, T., Cabanillas, V.R., Feng, B.: Exponential and polynomial stabilization of laminated beams with two history memories. Math. Control Relat. Fields 13(4), 1258–1281 (2023). https://doi.org/10.3934/mcrf.2022037

    Article  MathSciNet  Google Scholar 

  34. Raposo, C., Bastos, W., Santos, M.: A transmission problem for the Timoshenko system. Comput. Appl. Math. 26(2), 215–234 (2007). https://doi.org/10.1590/S0101-82052007000200003

    Article  MathSciNet  Google Scholar 

  35. Raposo, C., Ferreira, J., Santos, M., Castro, N.: Exponential stability for the Timoshenko system with two weak dam**s. Appl. Math. Lett. 18(5), 535–541 (2005). https://doi.org/10.1016/j.aml.2004.03.017

    Article  MathSciNet  Google Scholar 

  36. Raposo, C.: Exponential stability for a structure with interfacial slip and frictional dam**. Appl. Math. Lett. 53, 85–91 (2016). https://doi.org/10.1016/j.aml.2015.10.005

    Article  MathSciNet  Google Scholar 

  37. Reddy, J.N.: Mechanics of Laminated Composite Plates and Shells: Theory and Analysis. CRC Press, Boca Raton (2003)

    Book  Google Scholar 

  38. Soufyane, A.: Stabilisation de la poutre de Timoshenko. C. R. Acad. Sci. Paris Sér. I Math. 328(8), 731–734 (1999). https://doi.org/10.1016/S0764-4442(99)80244-4

    Article  MathSciNet  Google Scholar 

  39. Tatar, N.E.: Stabilization of a viscoelastic Timoshenko beam. Appl. Anal. 92(1), 27–43 (2013). https://doi.org/10.1080/00036811.2011.587810

    Article  MathSciNet  Google Scholar 

  40. Tatar, N.E.: Stabilization of a laminated beam with interfacial slip by boundary controls. Bound. Value Probl. 2015, 169 (2015). https://doi.org/10.1186/s13661-015-0432-3

    Article  MathSciNet  Google Scholar 

  41. Timoshenko, S.: On the correction for shear of the differential equation for transverse vibrations of prismatic bars. Philos. Mag. 41, 744–746 (1921). https://doi.org/10.1080/14786442108636264

    Article  Google Scholar 

  42. Volterra, V.: Sur les équations intégro-différentielles et leurs applications. Acta Math. 35, 295–356 (1912). https://doi.org/10.1007/BF02418820

    Article  MathSciNet  Google Scholar 

  43. Volterra, V., Lecons sur les fonctions de lignes professées a la Sorbonne en,: Recueillies et redigées par Joseph Pérès. Paris, Gauthier-Villars 1913, 230 (1912). https://doi.org/10.1007/bf01999460

  44. Wang, J.M., Xu, G.Q., Yung, S.P.: Exponential stabilization of laminated beams with structural dam** and boundary feedback controls. SIAM J. Control Optim. 44(5), 1575–1597 (2005). https://doi.org/10.1137/040610003

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

The authors thank the anonymous reviewers for their suggestions and valuable comments.

Author information

Author notes

  1. Victor R. Cabanillas, Teófanes Quispe Méndez, Carlos Quicaño Barrientos have contributed equally to this work.

Authors and Affiliations

  1. Programa de Estudios Generales, Universidad de Lima, Avenida Javier Prado Este 4600, 15023, Lima, Peru

    Victor R. Cabanillas

  2. Facultad de Ciencias Matemáticas, Universidad Nacional Mayor de San Marcos, Calle Germán Amézaga 375, 15081, Lima, Peru

    Victor R. Cabanillas, Teófanes Quispe Méndez & Carlos Quicaño Barrientos

Authors
  1. Victor R. Cabanillas
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Teófanes Quispe Méndez
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Carlos Quicaño Barrientos
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Victor R. Cabanillas.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Cabanillas, V.R., Quispe Méndez, T. & Quicaño Barrientos, C. The effect of Kelvin–Voigt dam** on the stability of Timoshenko laminated beams system with history. Rend. Circ. Mat. Palermo, II. Ser (2024). https://doi.org/10.1007/s12215-024-01081-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s12215-024-01081-9

Keywords

Mathematics Subject Classification

Search

Navigation