SpringerLink
Log in

Time-fractional nonlinear evolution of dynamic wave propagation using the Burgers’ equation

  • Original Research
  • Published:
Journal of Applied Mathematics and Computing Aims and scope Submit manuscript

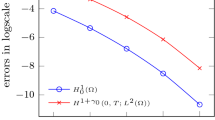
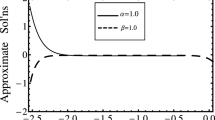
Abstract

Fractional derivatives are crucial in diverse contexts, offering a means to extend classical derivatives to noninteger orders. This expansion of calculus enables a more detailed understanding of complex behaviors in scientific, engineering, and mathematical disciplines. In this study, we use theoretical and numerical analyses to thoroughly examine the time-fractional Burgers’ equation. Our main emphasis is on deriving time-decay estimates for solutions within a bounded domain. To determine optimal time-decay rates, we introduce a linear compact difference scheme by integrating an \(L_1\) discretization formula for the Caputo derivative and compact difference operators with spatial derivatives. We provide a detailed analysis encompassing existence and uniqueness, and an error estimate of solutions under the \(\Vert \cdot \Vert _{\infty }\) norm for the proposed scheme. Comprehensive numerical experiments highlight the efficiency and robustness of our approach, ensuring reliability for long-time simulations. Furthermore, numerical results are scrutinized to pinpoint the optimal time-decay rate. This work explores the asymptotic behavior of solutions to the time-fractional Burgers’ equation and the development of linear high-order accuracy difference methods for nonlinear time-fractional equations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
EUR 32.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or Ebook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Thailand)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

Data availability

The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

References

  1. Bomers, A., Schielen, R.M.J., Hulscher, S.J.M.H.: The influence of grid shape and grid size on hydraulic river modelling performance. Environ. Fluid Mech. 19, 1273–1294 (2019)

    Article  Google Scholar 

  2. Mairal, J., Murillo, J., Navarro, P.G.: The entropy fix in augmented Riemann solvers in presence of source terms: application to the Shallow Water Equations. Comput. Methods Appl. Mech. Eng. 417, 116411 (2023)

    Article  MathSciNet  Google Scholar 

  3. Khater, M.M.: Numerous accurate and stable solitary wave solutions to the generalized modified equal-width equation. Int. J. Theor. Phys. 62, 151 (2023)

    Article  MathSciNet  Google Scholar 

  4. Khater, M.M.: In surface tension; gravity-capillary, magneto-acoustic, and shallow water waves’ propagation. Eur. Phys. J. Plus 138, 320 (2023)

    Article  Google Scholar 

  5. Khater, M.M.: Prorogation of waves in shallow water through unidirectional Dullin–Gottwald–Holm model; computational simulations. Int. J. Mod. Phys. B 37(8), 2350071 (2023)

    Article  Google Scholar 

  6. Khater, M.M.: Long waves with a small amplitude on the surface of the water behave dynamically in nonlinear lattices on a non-dimensional grid. Int. J. Mod. Phys. B 37(19), 2350188 (2023)

    Article  Google Scholar 

  7. Magadlena, I., Marcela, I., Karima, M., Jonathan, G., Harlan, D., Adityawan, M.B.: Two layer shallow water equations for wave attenuation of a submerged porous breakwater. Appl. Math. Comput. 454, 128096 (2023)

    MathSciNet  Google Scholar 

  8. Lekhooana, M., Molati, M.: Nonlinear long waves in shallow water for normalized Boussinesq equations. Results Phys. 59, 107614 (2024)

    Article  Google Scholar 

  9. Zhao, F., Gan, J., Xu, K.: High-order compact gas-kinetic scheme for two-layer shallow water equations on unstructured mesh. J. Comput. Phys. 498, 112651 (2024)

    Article  MathSciNet  Google Scholar 

  10. Dullo, T.T., Gangrade, S., Morales-Hernandez, M., Sharif, M.B., Kalyanapu, A.J., Kao, S.-C., Ghafoor, S., Ashfaq, M.: Assessing climate change-induced flood risk in the Conasauga river watershed: an application of ensemble hydrodynamic inundation modeling. Natl. Hazards Earth Syst. Sci. 1–54 (2020)

  11. Minatti, L., Faggioli, L.: The exact Riemann solver to the shallow sater equations for natural channels with bottom steps. Comput. Fluids 254, 105789 (2023)

    Article  Google Scholar 

  12. Khater, M.M.: Computational simulations of propagation of a tsunami wave across the ocean. Chaos Solitons Fractals 174, 113806 (2023)

    Article  MathSciNet  Google Scholar 

  13. Khater, M.M.: Characterizing shallow water waves in channels with variable width and depth: computational and numerical simulations. Chaos Solitons & Fractals 173, 113652 (2023)

    Article  MathSciNet  Google Scholar 

  14. Khater, M.M.: Computational and numerical wave solutions of the Caudrey–Dodd–Gibbon equation. Heliyon 9, e13511 (2023)

    Article  Google Scholar 

  15. Issa, R., Rouge, D., Benoit, M., Violeau, D., Joly, A.: Modelling algae transport in coastal areas with a shallow water equation model including wave effects. J. Hydro-Environ. Res. 3(4), 215–223 (2010)

    Article  Google Scholar 

  16. Hu, K., Mingham, C.G., Causon, D.M.: Numerical simulation of wave overtop** of coastal structures using the non-linear shallow water equations. Coast. Eng. 41(4), 433–465 (2000)

    Article  Google Scholar 

  17. Xu, Y., Yu, X.: Enhanced formulation of wind energy input into waves in develo** sea. Prog. Oceanogr. 186, 102376 (2020)

    Article  Google Scholar 

  18. Li, X., Li, M., Jordan, L.-B., McLelland, S., Parsons, D.R., Amoudry, L.O., Song, Q., Comerford, L.: Modelling impacts of tidal stream turbines on surface waves. Renew. Energy 130, 725–734 (2019)

    Article  Google Scholar 

  19. Brown, S.A., Ransley, E.J., **e, N., Monk K., De Angelis, G.M., Nicholls-Lee, R., Guerrini, E., Greaves, D.M.: On the impact of motion-thrust coupling in floating tidal energy applications. Appl. Energy 282(Part B), 116246 (2021)

  20. Rony, J.S., Chaitanya Sai, K., Karmakar, D.: Numerical investigation of offshore wind turbine combined with wave energy converter. Mar. Syst. Ocean Technol. 18, 14–44 (2023)

  21. Bateman, H.: Some recent researches on the motion of fluids. Mon. Weather Rev. 43(4), 163–170 (1915)

    Article  Google Scholar 

  22. Burgers, J.M.: A mathematical model illustrating the theory of turbulence. Adv. Appl. Mech. 1, 171–199 (1948)

    Article  MathSciNet  Google Scholar 

  23. Ramos, J.I.: Shock waves of viscoelastic Burgers’ equations. Int. J. Eng. Sci. 149, 103226 (2020)

    Article  MathSciNet  Google Scholar 

  24. Cole, J.D.: On a quasi-linear parabolic equation occurring in aerodynamics. Q. Appl. Math. 9(3), 225–236 (1951)

    Article  MathSciNet  Google Scholar 

  25. Cenesiz, Y., Baleanu, D., Kurt, A., Tasbozan, O.: New exact solutions of Burgers’ type equations with conformable derivative. Waves Random Complex Media 27(1), 103–116 (2017)

    Article  MathSciNet  Google Scholar 

  26. Albeverio, S., Korshunova, A., Rozanova, O.: A probabilistic model associated with the pressureless gas dynamics. Bull. Sci. Math. 137(7), 902–922 (2013)

    Article  MathSciNet  Google Scholar 

  27. Sugimoto, N.: Burgers’ equation with a fractional derivative; hereditary effects on nonlinear acoustic waves. J. Fluid Mech. 225, 631–653 (1991)

    Article  MathSciNet  Google Scholar 

  28. Inc, M.: The approximate and exact solutions of the space-and time-fractional Burgers’ equations with initial conditions by variational iteration method. J. Math. Anal. Appl. 345(1), 476–484 (2008)

    Article  MathSciNet  Google Scholar 

  29. Khater, M.M.: Multi-vector with nonlocal and non-singular kernel ultrashort optical solitons pulses waves in birefringent fibers. Chaos Solitons Fractals 167, 113098 (2023)

    Article  MathSciNet  Google Scholar 

  30. Altuijri, R., Abdel-Aty, A.-H., Nisar, K.S., Khater, M.M.: Exploring plasma dynamics: analytical and numerical insights into generalized nonlinear time fractional Harry Dym equation. Mod. Phys. Lett. B (2024). https://doi.org/10.1142/S0217984924502646

    Article  Google Scholar 

  31. Khater, M.M.: Wave propagation analysis in the modified nonlinear time fractional Harry Dym equation: insights from Khater II method and B-spline schemes. Mod. Phys. Lett. B (2024). https://doi.org/10.1142/S0217984924400037

    Article  Google Scholar 

  32. Zhang, Y., Wang, Z.: Numerical simulation for time-fractional diffusion-wave equations with time delay. J. Appl. Math. Comput. 69, 137–157 (2023)

    Article  MathSciNet  Google Scholar 

  33. Zhang, L., Lu, K., Wang, G.: An efficient numerical method based on Chelyshkov operation matrix for solving a type of time-space fractional reaction diffusion equation. J. Appl. Math. Comput. 70, 351–374 (2024)

    Article  MathSciNet  Google Scholar 

  34. Roul, P., Rohil, V., Paredes, G.E., Obaidurrahman, K.: Numerical approximation of a fractional neutron diffusion equation for neutron flux profile in a nuclear reactor. Prog. Nucl. Energy 170, 105144 (2024)

    Article  Google Scholar 

  35. Cao, H., Cheng, X., Zhang, Q.: Numerical simulation methods and analysis for the dynamics of the time-fractional KdV equation. Physica D 460, 134050 (2024)

    Article  MathSciNet  Google Scholar 

  36. Momani, S.: Non-perturbative analytical solutions of the space- and time-fractional Burgers’ equations. Chaos Solutions and Fractals 28, 930–937 (2006)

    Article  MathSciNet  Google Scholar 

  37. Yildirim, A., Mohyud-Din, S.T.: Analytical approach to space- and time-fractional Burgers’ equations. Chin. Phys. Lett. 27, 090501 (2010)

    Article  Google Scholar 

  38. Khan, N.A., Ara, A., Mahmood, A.: Numerical solutions of time-fractional Burgers’ equations: a comparison between generalized differential transformation technique and homotopy perturbation method. Int. J. Numer. Methods Heat Fluid Flow 22, 175–193 (2012)

    Article  MathSciNet  Google Scholar 

  39. Yokus, A., Kaya, D.: Numerical and exact solutions for time fractional Burgers’ equation. J. Nonlinear Sci. Appl. 10, 3419–3428 (2017)

    Article  MathSciNet  Google Scholar 

  40. Asgari, Z., Hosseini, S.M.: Efficient numerical schemes for the solution of generalized time fractional Burgers’ type equations. Numer. Algorithms 77, 763–792 (2018)

    Article  MathSciNet  Google Scholar 

  41. Esen, A., Tasbozan, O.: Numerical solution of time fractional Burgers’ equation by cubic B-spline finite elements. Mediterr. J. Math. 13, 1325–1337 (2016)

    Article  MathSciNet  Google Scholar 

  42. Yaseen, M., Abbas, M.: An efficient computational technique based on cubic trigonometric B-splines for time fractional Burgers’ equation. Int. J. Comput. Math. 97, 725–738 (2020)

    Article  MathSciNet  Google Scholar 

  43. Oruc, O., Esen, A., Bulut, F.: A unified finite difference Chebyshev wavelet method for numerically solving time fractional Burgers’ equation. Discrete Contin. Dyn. Syst. B 12, 533–542 (2019)

    MathSciNet  Google Scholar 

  44. Wang, H., Xu, D., Zhou, J., Guo, J.: Weak Galerkin finite element method for a class of time fractional generalized Burgers’ equation. Numer. Methods Partial Differ. Equ. 37(1), 732–749 (2021)

    Article  MathSciNet  Google Scholar 

  45. Hussein, A.J.: A weak Galerkin finite element method for solving time-fractional coupled Burgers’ equations in two dimensions. Appl. Numer. Math. 156, 265–275 (2020)

    Article  MathSciNet  Google Scholar 

  46. Zhang, Y., Feng, M.: A local projection stabilization virtual element method for the time-fractional Burgers’ equation with high Reynolds numbers. Appl. Math. Comput. 436, 127509 (2023)

    MathSciNet  Google Scholar 

  47. Li, D., Zhang, C., Ran, M.: A linear finite difference scheme for generalized time fractional Burgers’ equation. Appl. Math. Model. 40(11–12), 6069–6081 (2016)

    Article  MathSciNet  Google Scholar 

  48. Qiu, W., Chen, H., Zheng, X.: An implicit difference scheme and algorithm implementation for the one-dimensional time-fractional Burgers’ equations. Math. Comput. Simul. 166, 298–314 (2019)

    Article  MathSciNet  Google Scholar 

  49. Qiao, L., Tang, B.: An accurate, robust, and efficient finite difference scheme with graded meshes for the time-fractional Burgers’ equation. Appl. Math. Lett. 128, 107908 (2022)

    Article  MathSciNet  Google Scholar 

  50. Li, S.: Numerical analysis for fourth-order compact conservative difference scheme to solve the 3D Rosenau-RLW equation. Comput. Math. Appl. 72(9), 2388–2407 (2016)

    Article  MathSciNet  Google Scholar 

  51. Wang, X., Zhang, Q., Sun, Z.Z.: The pointwise error estimates of two energy-preserving fourth-order compact schemes for viscous Burgers’ equation. Adv. Comput. Math. 47, 1–42 (2021)

    Article  MathSciNet  Google Scholar 

  52. He, Y., Wang, X., Zhong, R.: A new linearized fourth-order conservative compact difference scheme for the SRLW equation. Adv. Comput. Math. 48(3), 27 (2022)

    Article  MathSciNet  Google Scholar 

  53. Peng, X., Xu, D., Qiu, W.: Pointwise error estimates of compact difference scheme for mixed-type time-fractional Burgers’ equation. Math. Comput. Simul. 208, 702–726 (2023)

    Article  MathSciNet  Google Scholar 

  54. Gao, G.H., Sun, Z.Z.: Compact difference schemes for heat equation with Neumann boundary conditions (II). Numer. Methods Partial Differ Equ. 29(5), 1459–1486 (2013)

    Article  MathSciNet  Google Scholar 

  55. Li, X., Zhang, L., Wang, S.: A compact finite difference scheme for the nonlinear Schrodinger equation with wave operator. Appl. Math. Comput. 219(6), 3187–3197 (2012)

    MathSciNet  Google Scholar 

  56. He, Y., Wang, X., Cheng, H., Deng, Y.: Numerical analysis of a high-order accurate compact finite difference scheme for the SRLW equation. Appl. Math. Comput. 418, 126837 (2022)

    MathSciNet  Google Scholar 

  57. Wang, B., Sun, T., Liang, D.: The conservative and fourth-order compact finite difference schemes for regularized long wave equation. J. Comput. Appl. Math. 356, 98–117 (2019)

    Article  MathSciNet  Google Scholar 

  58. Long, J., Luo, C., Yu, Q., Li, Y.: An unconditional stable compact fourth-order finite difference scheme for three dimensional Allen-Cahn equation. Comput. Math. Appl. 77(4), 1042–1054 (2019)

    Article  MathSciNet  Google Scholar 

  59. Poochinapan, K., Wongsaijai, B.: Numerical analysis for solving Allen–Cahn equation in 1D and 2D based on higher-order compact structure-preserving difference scheme. Appl. Math. Comput. 434, 127374 (2022)

    MathSciNet  Google Scholar 

  60. Poochinapan, K., Wongsaijai, B.: High-performance computing of structure-preserving algorithm for the coupled BBM system formulated by weighted compact difference operators. Math. Comput. Simul. 205, 439–467 (2023)

    Article  MathSciNet  Google Scholar 

  61. Poochinapan, K., Wongsaijai, B.: Novel advances in high-order numerical algorithm for evaluation of the shallow water wave equations. Adv. Contin. Discrete Models 2023, 13 (2023). https://doi.org/10.1186/s13662-023-03760-w

    Article  MathSciNet  Google Scholar 

  62. Cui, M.: An alternating direction implicit compact finite difference scheme for the multi-term time-fractional mixed diffusion and diffusion wave equation. Math. Comput. Simul. (2023)

  63. Zhang, Q., Sun, C., Fang, Z.W., Sun, H.W.: Pointwise error estimate and stability analysis of fourth-order compact difference scheme for time-fractional Burgers’ equation. Appl. Math. Comput. 418, 126824 (2022)

    MathSciNet  Google Scholar 

  64. Dipierro, S., Valdinoci, E., Vespri, V.: Decay estimates for evolutionary equations with fractional time-diffusion. J. Evol. Equ. 19, 435–462 (2019)

    Article  MathSciNet  Google Scholar 

  65. Smadiyeva, A.G., Torebek, B.T.: Decay estimates for the time-fractional evolution equations with time-dependent coefficients. Proc. R. Soc. A Math. Phys. Eng. Sci. 479(2276), 20230103 (2023)

    MathSciNet  Google Scholar 

  66. D’Abbicco, M., Girardi, G.: Decay estimates for a perturbed two terms space–time fractional diffusive problem. Evol. Equ. Control Theory 12(4), 1056–1082 (2023)

  67. Jeffrey, A., Zhao, H.: Global existence and optimal temporal decay estimates for system parabolic conservation lawsI. The one-dimensional case. J. Math. Anal. Appl. 70(1–2), 175–193 (1998)

    Google Scholar 

  68. Chern, I.L., Liu, T.P.: Convergence to diffusion waves of solutions for viscous conservation laws. Commun. Math. Phys. 110, 503–517 (1987)

    Article  MathSciNet  Google Scholar 

  69. Vergara, V., Zacher, R.: Optimal decay estimates for time-fractional and other nonlocal subdiffusion equations via energy methods. SIAM J. Math. Anal. 47(1), 210–239 (2015)

    Article  MathSciNet  Google Scholar 

  70. Kemppainen, J., Zacher, R.: Long-time behaviour of non-local in time Fokker–Planck equations via the entropy method. Math. Models Methods Appl. Sci. 29(02), 209–235 (2019)

    Article  MathSciNet  Google Scholar 

  71. Paris, R.B.: Exponential asymptotics of the Mittag–Leffler function. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 458(2028), 3041–3052 (2002)

    Article  MathSciNet  Google Scholar 

  72. Wang, T., Guo, B., Xu, Q.: Fourth-order compact and energy conservative difference schemes for the nonlinear Schrodinger equation in two dimensions. J. Comput. Phys. 243, 382–399 (2013)

    Article  MathSciNet  Google Scholar 

  73. Hao, Z.P., Sun, Z.Z., Cao, W.R.: A three-level linearized compact difference scheme for the Ginzburg–Landau equation. Numer. Methods Partial Differ. Equ. 31(3), 876–899 (2015)

    Article  MathSciNet  Google Scholar 

  74. Sun, Z.Z., Wu, X.: A fully discrete difference scheme for a diffusion-wave system. Appl. Numer. Math. 56(2), 193–209 (2006)

    Article  MathSciNet  Google Scholar 

  75. Sun, Z.: Numerical Methods for Partial Differential Equations, 2nd edn. Science Press, Bei**g (2012)

    Google Scholar 

  76. Dimitrienko, Y.I., Li, S., Niu, Y.: Study on the dynamics of a nonlinear dispersion model in both 1D and 2D based on the fourth-order compact conservative difference scheme. Math. Comput. Simul. 182, 661–689 (2021)

    Article  MathSciNet  Google Scholar 

  77. Liao, H.L., Li, D., Zhang, J.: Sharp error estimate of the nonuniform L1 formula for linear reaction–subdiffusion equation. SIAM J. Numer. Anal. 56(2), 1112–1133 (2018)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

This research was supported by Chiang Mai University, Thailand.

Funding

This research was supported by Chiang Mai University and Fundamental Fund 2024, Chiang Mai University.

Author information

Authors and Affiliations

  1. Department of Mathematics, Faculty of Science, Chiang Mai, 50200, Thailand

    Sivaporn Phumichot, Kanyuta Poochinapan & Ben Wongsaijai

  2. Advanced Research Center for Computational Simulation, Chiang Mai University, Chiang Mai, 50200, Thailand

    Kanyuta Poochinapan & Ben Wongsaijai

Authors
  1. Sivaporn Phumichot
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Kanyuta Poochinapan
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Ben Wongsaijai
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

Sivaporn Phumichot: Conceptualization, Formal analysis, Investigation, Methodology, Software, Validation, Writing-original draft, and Writing-review and editing; Kanyuta Poochinapan: Formal analysis, Funding acquisition, Investigation, Methodology, Supervision, Validation, Visualization, and Writing-review and editing, Ben Wongsaijai: Conceptualization, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Validation, Visualization, Writing-original draft, and Writing-review and editing.

Corresponding author

Correspondence to Ben Wongsaijai.

Ethics declarations

Conflict of interest

No Conflict of interest exists. We wish to confirm that there are no known Conflict of interest associated with this publication and there has been no significant financial support for this work that could have influenced its outcome.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Phumichot, S., Poochinapan, K. & Wongsaijai, B. Time-fractional nonlinear evolution of dynamic wave propagation using the Burgers’ equation. J. Appl. Math. Comput. (2024). https://doi.org/10.1007/s12190-024-02100-9

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s12190-024-02100-9

Keywords

Search

Navigation