SpringerLink
Log in

How Strain-Rate Sensitivity Creates Two Forming-Limit Diagrams: Bragard-Type Versus Instability-Strain, Correlation-Coefficient-Based Temporal Curves

  • Published:
Journal of Materials Engineering and Performance Aims and scope Submit manuscript

Abstract

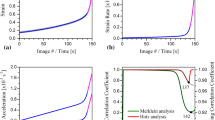
With digital-image correlation techniques, it is now possible to measure the forming-limit diagram, FLD, of metal sheet using both strains outside (Bragard-type analysis) and inside (temporal, correlation-coefficient calculation) of a necking instability. We performed these measurements using the Marciniak and Kuczynski, MK, specimen geometry on three metals having very different strain-rate sensitivities: Zn20, a Zn-Cu-Ti alloy; a cold-rolled steel; and an AA6061-T4 aluminum alloy. The relationship between the Bragard type and temporal FLDs was very different depending on the metal’s strain-rate sensitivity. For the highly strain-rate sensitive Zn20, m = 0.075, the temporal FLD was well above the Bragard type for all strain states, from uniaxial tension to balanced-biaxial deformation. In the case of the cold-rolled steel, m = 0.015, the two analyses were equivalent in balanced-biaxial deformation, but the temporal results were higher in plane-strain and uniaxial tension, by 25 and 40%, respectively. The two types of FLD curves were equivalent for all strain states for the AA6061-T4 aluminum alloy, m = zero. In addition, we found that the strain paths followed by the three metals were different for the same MK sample geometries. These differences were due to different shapes of the yield/flow loci, as confirmed based on visco-plastic self-consistent simulations. These results indicate that engineers should account for the different FLDs for positive strain-rate sensitive metals, possibly as upper and lower bounds. In addition, it appears that for metals with yield/flow loci like that of the AA6061-T4 aluminum alloy, certain strain paths between plane strain and balanced-biaxial deformation are difficult to attain when using the MK-type sample geometry.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

References

  1. J. Blaber, B. Adair and A. Antoniou, Ncorr: Open-Source 2D Digital Image Correlation Matlab Software, Exp. Mech., 2015, 55, p 1105–1122.

    Article  Google Scholar 

  2. A. Bragard, J.C. Baret and H. Bonnarens, A Simplified Technique to Determine the FLD at the Onset of Necking, Rapp. Centre Rech. Metall., 1972, 33, p 53–63.

    Google Scholar 

  3. M. Brunet, S. Mguil and F. Morestin, Analytical and Experimental Studies of Necking in Sheet Metal Forming Processes, J. Mater. Process., 1998, 80–81, p 40–46.

    Article  Google Scholar 

  4. G. Charca Ramos, M. Stout, R.E. Bolmaro, J.W. Signorelli and P. Turner, Study of a Drawing-Quality Sheet Steel. I: Stress/Strain Behaviors and Lankford Coefficients by Experiments and Micromechanical Simulations, Int. J. Solids Struct., 2010, 47, p 2285–2293.

    Article  Google Scholar 

  5. A.I. Durán, J.W. Signorelli, D.J. Celentano, M.A. Cruchaga and M. François, Experimental and Numerical Analysis on the Formability of a Heat-Treated AA1100 Aluminum Alloy Sheet, J. Mater. Eng. Perform., 2015, 24, p 4156–4170.

    Article  Google Scholar 

  6. A.K. Ghosh and S. Hecker, Failure in Thin Sheets Stretched Over Rigid Punches, Metall. Mater. Trans. A, 1975, 6A, p 1065–1074.

    Article  CAS  Google Scholar 

  7. A.K. Ghosh, The Infuence of Strain Hardening and Strain-Rate Sensitivity on Sheet Metal Forming, Trans. ASME J. Eng. Mater. Technol., 1977, 99(3), p 264–274.

    Article  CAS  Google Scholar 

  8. GOM, GOM Service Area [Online] (GOM, 2019). http://www.gom.com/metrology-systems/aramis.html. Accessed 20 Dec 2019

  9. W. Hotz, M. Merklein, A. Kuppert, H. Friebe and M. Klein, Time Dependent FLC Determination: Comparison of Different Algorithms to Detect the Onset of Unstable Necking Before Fracture, Key Eng. Mater., 2013, 549, p 397–404.

    Article  Google Scholar 

  10. International Standard ISO 12004-2:2008, Metallic Materials—Sheet and Strip: Determination of Forming-Limit Curves. Part 2—Determination of Forming-Limit Curves in the Laboratory, International Organization for Standardization, Geneva, 2008.

  11. R.A. Lebensohn, P. Ponte Castaneda, R. Brenner and O. Castelnau, Full-Field vs. Homogenization Methods to Predict Microstructure-Property Relationships of Polycrystalline Materials, Computational Methods for Microstructure-Property Relationships. S. Ghos, D.S. Dimiduk Ed., Springer, Berlin, 2011, p 393–441

    Chapter  Google Scholar 

  12. R.A. Lebensohn and C.N. Tomé, A Self-Consistent Anisotropic Approach for the Simulation of Plastic Deformation and Texture Development of Polycrystals: Application to Zirconium Alloys, Acta Metall. Mater., 1993, 41, p 2611–2624.

    Article  CAS  Google Scholar 

  13. M. Leonard, C. Moussa, A. Roatta, A. Seret and J.W. Signorelli, Continuous Dynamic Recrystallization in a Zn-Cu-Ti Sheet Subjected to Bilinear Tensile Strain, Mater. Sci. Eng. A, 2020, 789, p 1–11.

    Article  Google Scholar 

  14. M.E. Leonard, F. Ugo, M. Stout and J.W. Signorelli, A Miniaturized Device for the Measurement of Sheet Metal Formability Using Digital Image Correlation, Rev. Sci. Instrum., 2018, 085114, p 89–95.

    Google Scholar 

  15. Z. Marciniak and K. Kuczynski, Limit Strains in the Processes of Stretch-Forming Sheet Metal, Int. J. Mech. Sci., 1967, 9, p 609–620.

    Article  Google Scholar 

  16. A.J. Martínez-Donaire, F.J. García-Lomas and C. Vallellano, New Approaches to Detect the Onset of Localised Necking in Sheets under through-Thickness Strain Gradients, Mater. Des., 2014, 57, p 135–145.

    Article  Google Scholar 

  17. M. Merklein, A. Kuppert and M. Geiger, Time Dependent Determination of Forming Limit Diagrams, CIRP Ann. Manuf. Technol., 2010, 59, p 295–298.

    Article  Google Scholar 

  18. J. Min, T.B. Stoughton, J.E. Carsley and J. Lin, Coµµrison of DIC Methods of Determining Forming Limit Strains, in International Conference on Sustainable Materials Processing and Manufacturing, SMPM 2017. Procedia Manufacturing, vol. 7 (2017), pp. 668–674

  19. K. Nakazima, T. Kikuma and K. Hasuka, Study on the Formability of Steel Sheets, Yawata Technical Report, No. 264, 1968, p 8517–8530

  20. A. Roatta, M. Leonard, E. Nicoletti and J.W. Signorelli, Modeling Texture Evolution During Monotonic Loading of Zn-Cu-Ti Alloy Sheet Using Viscoplastic Self-Consistent Polycrystal Model, Int. J. Solids Struct., 2020, 860, p 158425.

    Google Scholar 

  21. A. Roatta, M. Stout and J.W. Signorelli, Determination of the Forming-Limit Diagram from Deformations within the Necking Instability, a New Approach, J. Mater. Eng. Perform., 2020, 29, p 4018–4031.

    Article  CAS  Google Scholar 

  22. F. Schlosser, J.W. Signorelli, M.E. Leonard, A. Roatta, M. Milesic and N. Bozzolo, Influence of the Strain Path Changes on the Formability of a Zinc Sheet, J. Mater. Process., 2019, 271, p 101–110.

    Article  CAS  Google Scholar 

  23. F. Schlosser, Desarrollo de la Modelización Multiescala en Agregados Policristalinos HCP Bajo Solicitación Mecánica Inducida en Curso de Procesos de Conformado. Validación Experimental en Chapas de Zinc Texturado, Ph.D. thesis, Universidad Nacional del Sur, Bahía Blanca, Argentina, 2018

  24. C.D. Schwindt, M.A. Bertinetti, L. Iurman, C.A. Rossit and J.W. Signorelli, Numerical Study of the Effect of Martensite Plasticity on the Forming Limits of a Dual-Phase Steel Sheet, Int. J. Mater. Forming, 2016, 9, p 499–517.

    Article  Google Scholar 

  25. C. Schwindt, F. Schlosser, M.A. Bertinetti, M. Stout and J.W. Signorelli, Experimental and Visco-Plastic Self-Consistent Evaluation of Forming Limit Diagrams for Anisotropic Sheet Metals: An Efficient and Robust Implementation of the M-K Model, Int. J. Plast., 2015, 73, p 62–99.

    Article  CAS  Google Scholar 

  26. M.J. Serenelli, M.A. Bertinetti and J.W. Signorelli, Investigation of the Dislocation Slip Assumption on Formability of BCC Sheet Metals, Int J Mech. Sci., 2010, 52, p 1723–1734.

    Article  Google Scholar 

  27. M.A. Sutton, J.-J. Orteu and H.W. Schreier, Image Correlation for Shape, Motion and Deformation Measurements, Springer, New York, 2009.

    Google Scholar 

  28. C.N. Tome, R.A. Lebensohn and U.F. Kocks, A Model for Texture Development Dominated by Deformation Twinning: Application to Zirconium Alloys, Acta Metall. Mater., 1991, 39, p 2667–2680.

    Article  CAS  Google Scholar 

  29. P. Vacher, A. Haddad and R. Arrieux, Determination of the Forming Limit Diagrams Using Image Analysis by the Correlation Method, CIRP Ann. Manuf. Technol., 1999, 48, p 227–230.

    Article  Google Scholar 

  30. D. Vysochinskiy, T. Coudert, O.S. Hopperstad and O. Lademo, Experimental Detection of Forming Limit Strains on Samples with Multiple Necks, J. Mater. Process., 2016, 227, p 216–226.

    Article  Google Scholar 

  31. K. Wang, J.E. Carsley, B. He, J. Li and L. Zhang, Measuring Forming Limit Strains with Digital Image Correlation Analysis, J. Mater. Process. Technol., 2014, 214, p 1120–1130.

    Article  CAS  Google Scholar 

Download references

Acknowledgments

The authors are grateful for the financial support provided by ANPCyT PICT-A 2017-2970. We also acknowledge the invaluable support of Fernando Ugo in performing the forming-limit and tension experiments.

Author information

Authors and Affiliations

  1. Instituto de Física Rosario (CONICET/UNR), Ocampo y Esmeralda, 2000, Santa Fe, Rosario, Argentina

    M. A. Bertinetti, A. Roatta, E. Nicoletti, M. Leonard, M. Stout & J. W. Signorelli

  2. Facultad de Ciencias Exactas, Ingeniería y Agrimensura, Universidad Nacional de Rosario Av. Pellegrini 250, 2000, Santa Fe, Rosario, Argentina

    M. A. Bertinetti, A. Roatta, M. Leonard & J. W. Signorelli

Authors
  1. M. A. Bertinetti
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. A. Roatta
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. E. Nicoletti
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. M. Leonard
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. M. Stout
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. J. W. Signorelli
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to J. W. Signorelli.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Bertinetti, M.A., Roatta, A., Nicoletti, E. et al. How Strain-Rate Sensitivity Creates Two Forming-Limit Diagrams: Bragard-Type Versus Instability-Strain, Correlation-Coefficient-Based Temporal Curves. J. of Materi Eng and Perform 30, 4183–4193 (2021). https://doi.org/10.1007/s11665-021-05745-w

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11665-021-05745-w

Keywords

Search

Navigation